Assignments for Class 10 Mathematics Trigonometry have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Trigonometry from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Trigonometry. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Trigonometry book and get good marks in class 10 exams.
Question. If xcosθ – ycosθ = a, xsinθ + ycosθ = b , then x2 + y2 = ?
A) a+b
B) a2 +b2
C) a2 – b2
D) a-b
Answer
B
Question If sec2θ + cosec2θ can never be less than
A) 1
B) 0
C) -1
D) 2
Answer
D
Question. If sin = 1/2 then 3cosθ – 4cos θ
A) 0
B) 1
C) -1
D) 2
Answer
A
Question. secΦ + tanΦ = p, sinΦ = ?
A) (P+1) /P2-1
B) P2+1 /2P2 -1
C) P2-1 /P2 +1
D) None of these
Answer
C
Question. If 1– tanΘ/ 1–tanΘ = √(3 – 1) /√(3 + 1) then sinΘ /cos2Θ ?
A) 0
B) 1
C) 2
D) 3
Answer
B
Question. If 2x =secΘ and 2/x tanΘ , then find the value of 2 ( x2 – 1/x2)
A) 0
B) 1
C) 2
D) 3
Answer
B
Question. If 7sin2 θ + 3cos2θ = 4 then tanθ ?
A) 2/√3
B) 1/√3
C)-2/√3
D) 4/√3
Answer
B
Question. If cosΦ + sinΦ = √2 cosΦ then cosΦ – sinΦ
A) 2sinΦ
B) 2cosΦ
C) 2 sinΦ
D) 2 cosΦ
Answer
C
Question. If tan A+sin A = m and tan A-sin A = n then m2 – n2 ?
A) 4mn
B) 4 √mn
C) 2mn
D) 2√mn
Answer
B
Question. If secA = x+1/4x then sec A + tanA= ?
A) xor (1/X)
B) 2xor (1/2X)
C) 3xor (1/X)
D) 3xor (1/3X)
Answer
B
VERY SHORT ANSWER TYPE QUESTIONS
Question. The tops of two poles with heights 25 m and 35 m are connected by a wire, which makes an angle of elevation 30° at the top of 25 m pole. What is the length of the wire?
Answer
20 m
Question. A circus artist is climbing 24 m long rope, which is tightly stretched from the top of a vertical pole on the ground. If angle of elevation of the rope to the ground is 30°, what is the height of the pole?
Answer
12 m
Question. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Answer
8 √3 m
Question. In figure, An object A is observed from two light houses P and Q. What are the angles of depression from the observing light houses?
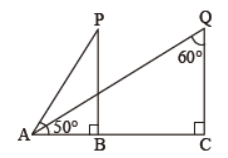
Answer
50° and 30° respectively
Question. In figure, what is the length of BC.
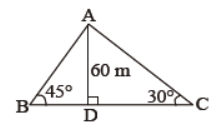
Answer
60 ( √3 +1) m
Question. A person standing on the bank of a river observe the angle of elevation of tree is 60°. When he moves 40 m away, the angle of elevation becomes 30°. At what distance is he now standing away from tree?
Answer
60 m
Question. In figure, the pole AB is 10 m away from a point C on the ground. What is the height of the pole?
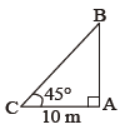
Answer
10 m
Question. A girl of height 170 cm stands in front of a lamp-post and casts a shadow of length 170 √3 cm on the ground. Find the angle of elevation of the top of the lamp-post.
Answer
30°
Question. The ratio of the length of a rod and its shadow is √3 :1. Find the angle of elevation of the sun.
Answer
60°
Question. If the steel wire tied to the top of the tower, makes an angle of 60° with the ground, then what is the length of the wire, if height of the tower is 18 m.
Answer
12 √3 m
Trigonometric Ratios
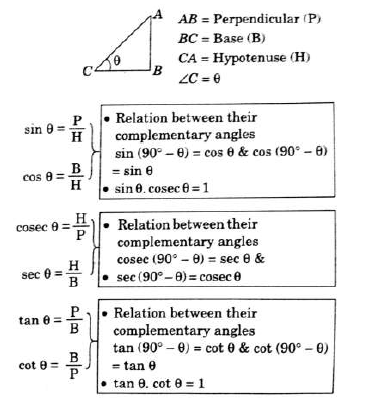
Trigonometric Identities
Relationship between trigonometric ratio that holds true for any value of θ
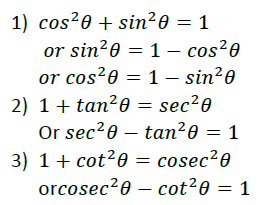
Question. If sec2θ (1 + sinθ)(1 – sinθ) = k, then find the value of k.
Sol. sec 2 θ (1 +sinθ)(1 -sinθ) = sec2θ (1 -sin2θ) [(a + b)(a – b) = a2 – b2]
= sec2θ .cos2θ [∴ cos2θ+sin2θ =1]
= 1
∴ k =1.
Question. If sin A = 3/4 calculate cos A and tan A.
Sol

Question. If sin A +sin2 A =1, then cos2 A +cos4 A =1.
Sol. True,
sin A +sin2A =1 ⇒ sin A =1 -sin2A = cos2A
∴ cos2A +cos4A = sin A +sin2A =1.
Question. If cot θ= 7/8 evaluate: (i) (1+sinθ) (1-sinθ)/(1+cosq) (1-cosθ), (ii) cot 2θ
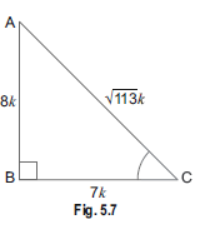
Sol. Let us draw a right triangle ABC in which ∠B = 90° and ∠C = θ.
We have

Question. tan47°/cot73°=1
Sol. True,
tan47°/cot73°=tan(90°-43° )/cot43°= cot43°/cot43°
Question. In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
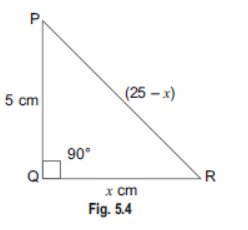
Sol. We have a right-angled ΔPQR in which ∠Q = 90°.
Let QR = x cm
Therefore, PR = (25 – x) cm
By Pythagoras Theorem, we have
PR2 = PQ2 + QR2
(25 – x)2 = 52 + x 2
⇒ (25 – x)2 – x 2 = 52
⇒ (25 – x – x) (25 – x + x) = 25
⇒ (25 – 2x) 25 = 25 Þ 25 – 2x =1
⇒ 25 -1 = 2x ⇒ 24 = 2x
∴ x =12 cm.
Hence, QR =12 cm
PR = (25 – x) cm = 25 -12 =13 cm
PQ = 5 cm
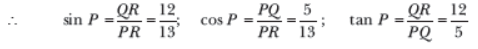
Question. If A + B = 90° and tan A = 3/4 , what is cot B ?
Sol. cot B = cot (90°-A) (∴ A + B = 90°)
= tan A (∴ cot (90° -θ) = tanθ)
= 3/4.
Question. Given 15 cot A = 8, find sin A and sec A.
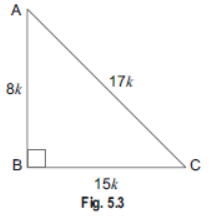
Sol. Let us first draw a right ΔABC, in which ∠B = 90°.
Now, we have, 15 cot A = 8

Question. The value of the expression (cos80° -sin80°) is negative.
Sol. True, for θ > 45° , sinθ > cosθ, so cos80° -sin80° has a negative value.
Question. If 3 cot A = 4, check whether 1-tan2A/1+tan2A=cos2Asin2A or not.
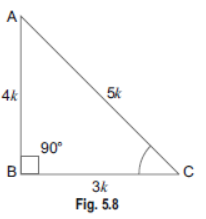
Sol. Let us consider a right triangle ABC in which ∠B= 90°.


Question. Write the acute angle θ satisfying 3 sinθ = cosθ.
Sol. 3 sinθ = cosθ
⇒ sinθ/cosθ 1/3 ⇒ tanθ = 1/3 ⇒ θ = 30°.
Question. (tanθ +2)(2tanθ +1) = 5tanθ +sec 2 θ.
Sol. False, (tanθ +2)(2tanθ +1) = 2tan2θ +5tanθ +2 = 5tanθ +2(1+tan2θ)
= 5tanθ +2sec2θ.
Question. Write the value of cot2θ=1/sin2θ
Sol. cot2θ=1/sin2θ= cot 2θ-cosec2θ =1.
Question. If sinθ = 1/3 , then find the value of 2cot 2 θ+2.
Sol.
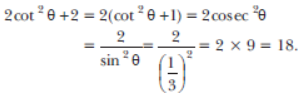
Question. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Sol. Let us consider a right-angled ΔABC in which ∠B = 90°.
For ∠A, we have
Base = AB
Perpendicular = BC
and Hypotenuse = AC

Question. Write all the other trigonometric ratios of ∠A in terms of sec A.
Sol. Let us consider a right-angled ΔABC, in which ∠B = 90°.
For ∠A, we have
Base = AB, Perpendicular = BC
and Hypotenuse = AC

Question. Evaluate : 5cos2 60° + 4sec2 30° – tan2 45°/sin2 30° + cos2 30°
Solution.
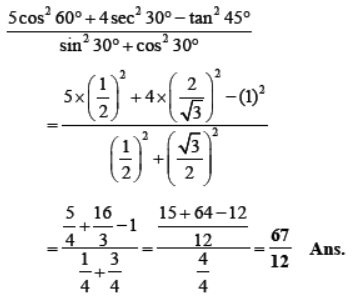
Question. If tan (A + B) = √3 and tan (A – B) = 1/√3 ; 0° < A + B ≤ 90°; A > B, find A and B.
Solution. tan (A + B) = √3 = tan 60° ⇒ A + B = 60°
and, tan (A B) = 1/√3 = tan 30° ⇒ A – B = 30°
On adding (1) and (2), we get, 2A = 90° ⇒ A = 45°
subtracting (2) from (1), we get, 2B = 30° ⇒ B = 15°
So, A = 45° and B = 15° Ans.
Question. Given : cotθ = 20/21 , find all other trigonometric ratios.
Solution.


Question. If 3 cot A = 4, check whether 1 – tan2 A /1 + tan2 A = cos2 A – sin2 A or not.
Solution.
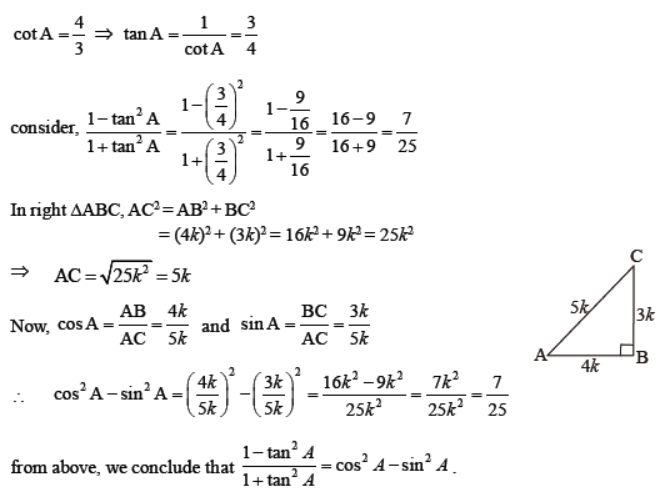
Question. If A, B, C are the interior angles of a triangle ABC, show that sin(B + C)/2 = cos A/2 .
Solution. We know, in any ΔABC, A + B + C = 180°
⇒ B + C = 180° – A
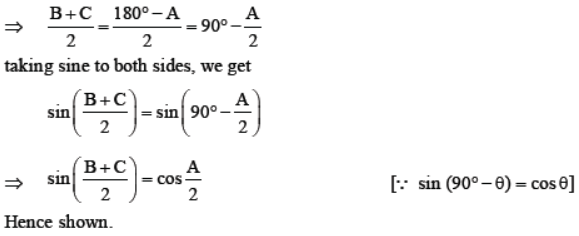
Question. Prove the following Trigonometric identities :
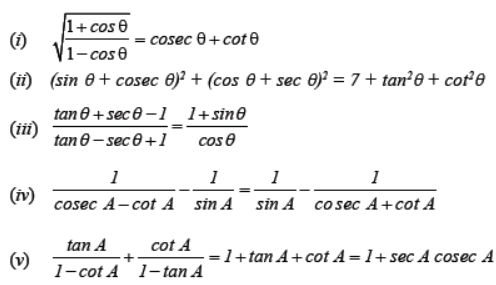
Solution.





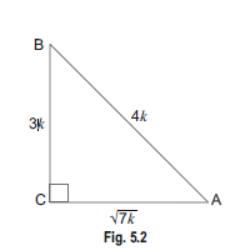
Question. In ΔABC, right angled at B, AB = 24 cm, BC = 7 cm. Determine : (i) sin A, cos A (ii) sin C, cos C
Solution. In right angled ΔABC, we have
AC2 = AB2 + BC2
⇒ AC2 = (24)2 + (7)2
⇒ AC2 = 576 + 49
⇒ AC2 = 625 ⇒ AC = 25

Question. (i) If tan θ + sin θ = m and tan θ – sin θ = n, show that m2 – n2 = 4 √mn.
(ii) If sec θ + tan θ = p, show that p2 – 1/p2 + 1 = sinθ
Solution. (i) We have, LHS = m2 – n2
= (tan θ + sin θ)2 – (tan θ – sin θ)2
= (tan2θ + sin2θ + 2tan θ . sin θ)– (tan2 θ + sin2θ – 2 tan θ sin θ)
= 4 tan θ sin θ
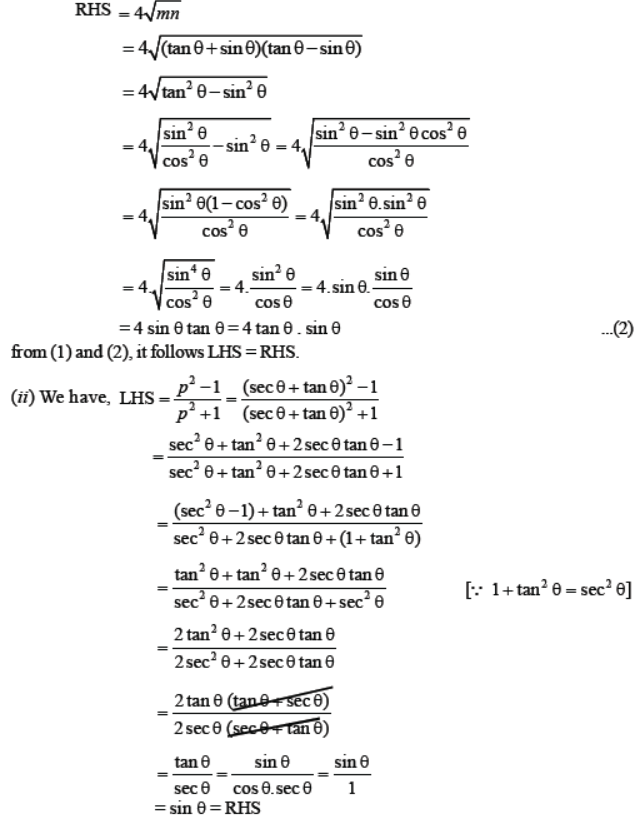
Question. Evaluate :
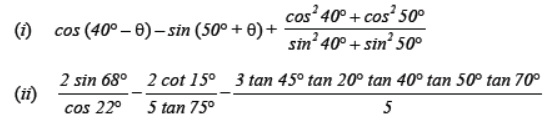
Solution.

Question. If tan2 A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution. We have, tan2A = cot (A – 18°) = tan [90° – (A – 18°)] [∴ cot θ = tan (90° – θ)]
= tan (108° – A)
⇒ 2A = 108° – A
⇒ 3A = 108° ⇒ A = 108°/3 ⇒ A = 36°Ans.
PRACTICE EXERCISE
Question. A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 meters away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and the width of the river.
Solution. height of tree = 34.64 m, width of river = 20 m
Question. A boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 30°. A girl standing on the roof of 20 metre high building, finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.
Solution. 30 √2 m
Question. Two men on either side of a cliff 80 m high observe the angles of elevation of top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
Solution. 184.64 m
Question. An aeroplane, when 1500 m high passes vertically above another aeroplane at an instance when the angles of the two aeroplanes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the two aeroplanes.
Solution. 634 m
Question. The angles of elevation of the top of a tower from two points on the ground at distances 9m and 4m from the base of the tower are in the same straight line with it are complementary. Find the height of the tower.
Solution. 6 m
Question. A flagstaff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flag-staff.
Solution. 3.65 m
Question. Two men are on the opposite sides of a tower. They measure the angles of elevation of the top of the towers as 30° and 45°. If the height of the tower is 60 m, find the distance between them.
Solution. 163.92 m
Question. An aeroplane, at an altitude of 200 m, observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.
Solution. 315.46 m
Question. From the top of a building 15 m high the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between the tower and the building.
Solution. Height = 22.5 m, Distance = 12.975 m
Question. At a point on the level ground the angle of elevation of a vertical tower is found to be such that its tangent is 5/12 . On walking 192 m towards the tower, the tangent of the angle is found to be 3/4 . Find the height of the tower.
Solution. 180 m
Question. The angles of depression of two ships from the top of a light house are 45° and 30°. If the ships are 200 m apart, find the height of the light house.
Solution. 273.2 m
Question. A man is standing on the deck of the a ship, which is 8 m above water level. He observes the angle of elevation of the top of the hill as 60° and the angle of depression of the base of the hill as 30°. Find the distance of the hill from the ship and the height of the hill.
Solution. 32 m and 8 √3 m
Question. The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower from the point A.
Solution. Height = 17.32 m, Distance = 30 m
Question. From the top of a hill, the angle of depression of two consecutive milestones due east are found to be 30° and 45°. Find the height of the hill.
Solution. √3 +1/2 miles
Question. The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m longer than when it was 60°. Find the height of the tower.
Solution. 23.66 m
Question. The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60 m, find the height of the first tower.
Solution. 140.73 m
Question. The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet plane is flying at a constant height of 1500 √3 m, find the speed of the jet plane.
Solution. 720 km/hr = 200 m/s
Question. The angle of elevation of the top of a hill at the foot of the tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50 m high, what is the height of the hill?
Solution. 150 m
Question. An observer in a lighthouse 100 m above the sea-level is watching the ship sailing towards the lighthouse.
The angle of depression of the ship from the observer is 30°. How far is the ship from the lighthouse?
Solution. 100 √3 m
Question. On a horizontal plane there is a vertical tower with a flag pole on the top of the tower. At a point 9 metres away from the foot of the tower the angle of elevation of the top and bottom of the flag pole are 60° and 30° respectively. Find the height of the tower and the flag pole mounted on it.
Solution. 3√3 m, 6√3 m
Question. From a point 30 m away from the foot the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower.
Solution. 17.32 m
Question. An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
Solution. 415.66 km/hr
Question. As observed from the top of a light-house, 100 m above sea level, the angle of depression of a ship sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during the period of observation.
Solution. 73.2 m
Question. An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Find the angle of elevation of the top of the tower from his eyes.
Solution. 45°
Question. Find the sun’s altitude when the height of a tower is √3 times of the length of its shadow.
Solution. 60°
Question. A 7 m long flagstaff is fixed on the top of a tower on the horizontal plane. From a point on the ground, the angle of elevation of the top and the bottom of the flagstaff are 45° and 30° respectively. Find the height of the tower correct to one place of decimal.
Solution. 9.6 m
Question. A man on the roof of a house which is 10 m high observes the angle of elevation of the top of a building as 45° and the angle of depression of the base of the building as 30°. Find the height of the building and its distance from the house.
Solution. Height of the building = 10 ( √3 +1) m, Distance of the building from house = 10 √3 m
Question. There is a small island in a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on the two banks and in the line with the tree. If the angles of elevation of the top of the tree from P and Q are 30° and 45° respectively, find the height of the tree.
Solution. 36.5 m
Question. From the top of a cliff 50 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 45° respectively. Find the height of the tower.
Solution. 21.17 m
Question. The angles of elevation and depression of the top and bottom of a light-house from the top of a building 60 m high, are 30° and 60° respectively. Find
(i) the difference between the heights of the light-house and the building.
(ii) distance between the light-house and the building.
Solution. (i) 20 m (ii) 34.64 m
Question. The horizontal distance between two towers is 75 m and the angle of depression of the top of the first tower as seen from the top of the second tower, which is 160 m high, is 45°. Find the height of the first tower.
Solution. 85 m
Question. The angle of elevation of a tower at a point is 45°. After going 40 m towards the foot of the tower, its angle of elevation becomes 60°. Find the height of the tower.
Solution. 94.64 m
Question. The angle of elevation θ of the top of a light house, as seen by a person on the ground is such that tanθ = 5/12 . When the person moves a distance of 240 m towards the light house, the angle of elevation becomes φ such that tan φ = 3/4 . Find the height of the light house.
Solution. 225 m
Question. A man on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower?
Solution. 16 minutes 23 seconds
Question. A bird is sitting on the top of a tree, which is 80 m high. The angle of elevation of the bird from a point on the ground is 45°. The bird flies away from the point of observation horizontally and remains at a constant height. After 2 seconds, the angle of elevation of the bird from the point of observation becomes 30°. Find the speed of the flying bird.
Solution. 29.28 m/s
Question. The upper part of a tree is broken by the action of wind. The top of the tree makes an angle of 45° with the horizontal ground. The distance between the base of the tree and the point where it touches the ground is 12 m. Find the height of the tree.
Solution. 28.92 m
Question. The angle of elevation of the top of an unfinished tower at a point distant 120 m from its base is 45°, how much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
Solution. 87.84 m
Question. From a point on the ground the angles of elevation of the bottom and top of a water tank kept at the top of 20 m high tower are 45° and 60°. Find the height of the water tank.
Solution. 14.60 m
Question. The angles of depression of the top and the bottom of a building, 50 metres high, as observed from the top of a tower are 30° and 60° respectively. Find the height of the tower and also the horizontal distance between the building and the tower.
Solution. 43.25 m and 75 m
Question. Standing on the top of a tower 100 m high, Abhishek observes two cars on the opposite sides of the tower. If their angles of depression are 60° and 45°, find the distance between the two cars.
Solution. 157.74 m
Question. A surveyor wants to find the height of the top of a hill. He observes that the angles of elevation of the top of the hill at points C and D, 300 m apart, lying on the base of the hill and on the same side of the hill are 30° and 45° respectively. What is the height of the hill.
Solution. 150( √3 +1) m
Question. An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
Solution. 415.2 km/hr (approx)
Question. A statue 1.6 m tall stands on the top of pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution. 2.184 m
Question. The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 65 m high, what is the height of the hill?
Solution. 195 m
Question. On the same side of the tower, two objects are located. Observed from the top of the tower, their angles of depressions are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
Solution. 63.4 m
Question. The horizontal distance between two trees of different heights is 90 m. The angle of depression of the top of the first tree when seen from the top of the second tree is 30°. If the height of the second tree is 72 m, find the height of the first tree.
Solution. 20.04 m
Question. From a building 60 m high, the angle of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance between the lamp post and building. Also find the difference of height between lamp post and building.
Solution. 20 √3 m and 20 m
Question. The angle of elevation of a cloud from a point 200 m above the lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
Solution. 400 m
Question. A boy is standing on the ground and is flying a kite with 100 m of string at an elevation of 30°. Another boy is standing on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of the kites. Find the length of the string that the second boy must have so that the two kites meet.
Solution. 40 √2 m
Question. A bridge across a river makes an angle of 30° with the river bank. If the length of the bridge across the river is 60 m, find the width of the river.
Solution. 40 m
Question. From the top of a tower 100 m, the angles of depression of the top and bottom of a pole standing on the same plane as the tower are observed to be 30° and 45° respectively. Find the height of the pole.
Solution. 42.26 m
Question. Two ships are sailing in the sea on the either side of the light-house, the angles of depression of two ships as observed from the top of the light-house are 60° and 45° respectively. If the distance between the ships is 200 (√3 + 1/√3) metres, find the height of the light-house.
Solution. 200 m
Question. A ladder is placed along a wall such that its upper end is touching the top of the wall. The foot of the ladder is 2m away from the wall and the ladder is making an angle of 60° with the level ground. Find the height of the wall.
Solution. 3.46 m
Question. The length of the shadow of a tower at a particular time is one-third of its shadow, when the sun’s rays meet the ground at an angle of 30°. Find the angle between the sun’s rays and the ground at the time of shorter shadow.
Solution. 60°
Assignments for Class 10 Mathematics Trigonometry as per CBSE NCERT pattern
All students studying in Grade 10 Mathematics Trigonometry should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Trigonometry exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Trigonometry which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.
Some advantages of Free Assignments for Class 10 Mathematics Trigonometry
- Solving Assignments for Mathematics Trigonometry Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
- By solving one assignments given in your class by Mathematics Trigonometry teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
- You will be able to understand the type of questions which are expected in your Mathematics Trigonometry class test
- You will be able to revise all topics given in the ebook for Class 10 Mathematics Trigonometry as all questions have been provided in the question banks
- NCERT Class 10 Mathematics Trigonometry Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
- Parents will be able to take print out of the assignments and give to their child easily.
All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Trigonometry teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Trigonometry Assignments PDF.
Free PDF download of Trigonometry Assignment Class 10 with Answers created by master educators from the latest syllabus of CBSE Boards. By practicing this Class 10 Trigonometry Assignments will help you to score more marks in your CBSE Board Examinations. We also give free NCERT Solutions and other study materials for students to make their preparation better.
Students who are searching for better solutions can download the Trigonometry Assignment Class 10 with answers to assist you with revising the whole syllabus and score higher marks in your exam.
This Trigonometry Assignment Class 10 with answers shows up with an answer key with step-by-step answers for students to comprehend the problem at each level and not retain it.

You can download free assignments for class 10 Mathematics Trigonometry from https://www.assignmentsbag.com
You can get free PDF downloadable assignments for Grade 10 Mathematics Trigonometry from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided assignments for all subjects in Grade 10, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge
Yes all test papers for Mathematics Trigonometry Class 10 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.
https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.

