Assignments for Class 9 Mathematics Polynomials have been developed for Standard 9 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 9 Mathematics Polynomials from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 9 Mathematics Polynomials. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Polynomials book and get good marks in class 9 exams.
Key Concepts for Class 9 Mathematics Polynomials
Constants : A symbol having a fixed numerical value is called a constant.
Example : 7, 3, -2, 3/7, etc. are all constants.
Variables : A symbol which may be assigned different numerical values is known as variable.
Example : C = 2π r C – circumference of circle
r – radius of circle
Where 2 & π are constants. while C and r are variable
Algebraic expressions : A combination of constants and variables. Connected by some or all of the operations +, -, X and ÷ is known as algebraic expression
Example : 4 + 9x – 5x2y + 3/8, xy etc
Terms : The several parts of an algebraic expression separated by ‘+’ or ‘-‘ operations are called the terms of the expression
Example : x2 + 2x2y + 4xy2 + y3 + 7 is an algebraic expression containing 5 terms x2, 3x3y, – 4xy2, y3 & 7
Polynomials : An algebraic expression in which the variables involved have only non-negative integral powers is called a polynomial.
(i) 5x3 – 4x2 – 6x – 3 is a polynomial in variable x.
(ii) 5 + 8x3/2 + 4x-2 is an expression but not a polynomial
Polynomials are denoted by p (x), q (x) and r (x) etc.
Coefficients : In the polynomial x3 + 3x2 + 1, coefficient of x3, x2, x are 1,3,3 respectively and we also say that +1 is the constant term in it.
Degree of a polynomial in one variable : In case of a polynomial in one variable the highest power of the variable is called the degree of the polynomial.
Classification of polynomials on the basis of degree.
degree Polynomial Example
(a) 1 Linear x + 1, 2x + 3 etc.
(b) 2 Quadratic etc. ax2 + bx + c etc.
(c) 3 Cubic etc. x3 – 3x2 + 1 etc
(d) 4 Biquadratic x4 – 1
Classification of polynomials on the basis of no. of terms
No. of terms Polynomial & Examples.
(i) 1 Monomial – 5, 3x, 1/3, y etc.
(ii) 2 Binomial – (3 + 6x), (x – 5y) etc.
(iii) 3 Trinomial – 2x2 + 4x + 2 etc.
Constant polynomial : A polynomial containing one term only, consisting a constant term is called a constant polynomial the degree of non-zero constant polynomial is zero.
Zero polynomial : A polynomial consisting of one term, namely zero only is called a zero polynomial.
The degree of zero polynomial is not defined.
Zeroes of a polynomial : Let p (x) be a polynomial. If p (a) = 0, then we say that α is a zero of the polynomial of p(x).
Remark : Finding the zeroes of polynomial p(x) means solving the equation p(x) = 0.
Remainder theorem : Let f (x) be a polynomial of degree n ≥ 1 and let a be any real number. When f (x) is divided by (x – α) then the remainder is (α)
Factor theorem : Let f (x) be a polynomial of degree n > 1 and let a be any real number.
(i) if (α) = 0 then (x – α) is factor of f (x)
(ii) if (x – α) is a factor of f (x) then f (a) = 0
Factor : A polynomial p (x) is called factor of q (x), if p (x) divides q (x) exactly.
Factorization : To express a given polynomial as the product of polynomials each of degree less than that of the given polynomial such that no such a factor has a factor of lower degree, is called factorization.
Example : x2 – 16 = (x + 4) (x – 4)
Methods of Factorization :
Factorization by taking out the common factor
e.g.
36q3b – 60a2bc = 12a2 (3a – 5c)
Factorizing by grouping
ab + bc + ax + cx = (ab + bc) + (ax + cx)
= (a + c) + x(a + c)
= (a + c) (b + x)
Factorization of quadratic trinomials by middle term splitting method.
x2 + bc + c = x2 + (p + q) x + pq
= ( x + p) ( x + q)
Identity : Identity is a equation (trigonometric, algebraic ) which is true for every value of variable.
Some algebraic identities useful in factorization:
(i) (x + y)2 = x2 + 2xy + y2
(ii) (x + y)2 = x2 – 2xy + y2
(iii) x2 – y2 = (x – y) (x +y)
(iv) (x +a) (x + b) = x2 + (a + b) x + ab
(v) (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
(vi) (x +y)3 = x3 + y3 + 3xy (x – y)
(vii) (x – y)3 = x3 – y3 – 3xy (x – y)
(viii) x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz -zx)
x3 + y3 + z3 = 3xyz if x + y + z = 0
Class 9 Mathematics Polynomials Assignments
Class 9 Mathematics Polynomials Important Questions and Answers
Question. Write the degree of each of the following polynomial.
(i) 2x – √5
Ans.
1
(ii) 3 – x + x2 – 6x3
Ans.
3
(iii) 9
Ans.
0
(vi) 8x4 – 36x + 5x7
Ans.
4
(v) x9 – x5 + 3x10 + 8
Ans.
9
(vi) 2 – 3x2
Ans.
2
Question. If x/y + y/x = -1 where x ≠ 0, y ≠ 0 then find the value of x3 – y3
Ans.
0
Question. The zeroes of the polynomial p(x) = 3x2 – 1 are
(a) 1/3
(b) 1/√3
(c) -1/√3
(d) 1/√3 and -1/√3
Ans.
1/√3 & -1/√3
Question. Find the zeros of the polynomials given below :
(i) p (x) = x – 5
Ans.
x = 5
(ii) q (x) = x + 4
Ans.
x = – 4
(iii) h (x) = 6x – 1
Ans.
x = 1/6
(vi) p (x) = ax + b
Ans.
x = – b/a
(v) r (x) = x2 + 3x
Ans.
x = 0, x = – 3
(vi) l (x) = x2 + 2x + 1
Ans.
x = – 1, – 1
Question. Which of the following expressions is polynomial?
(i) x5 – 2x3 + x + 7
(ii) y3 – √3y
(iii) 5√z – 6
(iv) x – (1/x)
(v) x108 – 1
(vi) 2vx – 27
(vii) x – 2 + 2x – 1 + 3
Ans.
(i), (ii), (v)
Question. Find the remainder when f (x) = 12x3 – 13x2 – 5x + 7 is divided by (3x + 2)?
Ans.
remainder = 1
Question. Factorize :
(i) 9x2 – 16y2
Ans.
(3x + 4y) (3x – 4y)
(ii) x3 – x
Ans.
x (x + 1) (x – 1)
Question. Find the value of a for which (x – a )is a factor of the polynomial.
f(x) = x5 – a2x3 + 2x + a – 3
Ans.
a = 1
Question. Factorize following expressions.
(i) x2 + 9 x + 18
Ans.
(x + 6) (x + 3)
(ii) x2 – 4x – 21
Ans.
(x -7) (x + 3)
(iii) x2 – 9x + 18
Ans.
(x – 6) (x – 3)
(iv) x2 – 19x + 78
Ans.
(x – 6) (x – 13)
Question. Calculate (997)2 using algebraic identities
Ans.
994009
Question. Factorize:
(i) a (a – 1) – b (b – 1)
Ans.
(a-b) (a+b-1)
Question. Calculate 103 X 107 using algebraic identities
Ans.
11021
Question. Expand (2a + 3b + 4c)2
Ans.
4a2 + 9b2 + 16c2 + 12zb + 12bc + 16ac
Question. Factorize 4x2 + y2 + z2 – 4xy – 2yz + 4xz
Ans.
(2x – y + z)2
Question. Expand
(i) (4a + 5b)2
Ans.
64a3 + 125b3 + 240a2b + 300qb2
(ii) (5x – 3y)3
Ans.
125x3 – 27y3 + 225x2y + 135xy2
Question. Evaluate
(i) (95)3
Ans.
857375
(ii) (106)3
Ans.
1191016
Question. Factorize the following expressions.
(i) 5x2 – 20 xy
Ans.
5x (x – 4y)
(ii) 5a (b + c) – 7b (b + c)
Ans.
(b + c) (5a – 7b)
(iii) x (x – y)2 + 3x2y (x – y)
Ans.
x (x – y) (x – y)
(iv) 6ab – b2 + 12ac – 3bc
Ans.
(b +2c) (6a – b)
(v) x2 + 1/x2 + 2 – 2x – (2/x)
Ans.
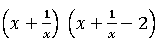
Question. Degree of zero polynomial is
(a) 1
(b) 0
(c) not defined
(d) none of these
Ans.
(c) not defined
Question. Factorize a3 + 27b3 + 8c3 – 18abc
Ans.
(a + 3b + 2c) (a2 + 9b2 +4c2 – 3ab – 6bc – 2ac)
Question. Factorize (p – q)3 (q -r)3 (r – p)3
Ans.
3(p – q) (q – r) (r – p)
Question. Find the product (3x – 5y – 4) (9x2 + 25y2 + 15xy + 12x – 20y + 16)
Ans.
27x3 – 125y3 – 64 – 180xy.
Question. Factorize
(i) x3 + 64
Ans.
(x + 4) (x2 – 4x + 16)
(ii) 27x3 + 125y3
Ans.
(3x + 5y) (9x2 – 15xy + 25y)2
(iii) 8a3 – 27b3
Ans.
(2a = 3b) (4a2 + 6ab + 9b2)
(iv) 1- 64a3
Ans.
(1 – 4a) (1 + 4a + 16a2)
Question. Which of the following expression is a polynomial?
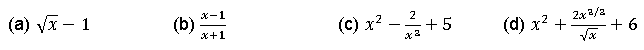
Ans.
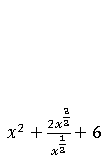
Question. If (x + 2) and (x – 1) are factors of (x2 + 10x2 + mx + n) then find value of m & n?
Ans.
m = 7, n = -18
Question. If if x + y + z = 9 and xy + yz + zx = 23 then find the value of (x3 + y3 + z3 – 3xyz)?
Ans.
108
Question. For what value of k is the polynomial p (x) = 2x3 – kx2 + 3x + 10 exactly divisible by (x + 2)?
(a) -1/3
(b) 1/3
(c) 3
(d) -3
Ans.
-3
Question. Find the value of (368)2 – (368)2
Ans.
737
Assignments for Class 9 Mathematics Polynomials as per CBSE NCERT pattern
All students studying in Grade 9 Mathematics Polynomials should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Polynomials exam for standard 9. We have made sure that all topics given in your textbook for Mathematics Polynomials which is suggested in Class 9 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.
Some advantages of Free Assignments for Class 9 Mathematics Polynomials
- Solving Assignments for Mathematics Polynomials Class 9 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
- By solving one assignments given in your class by Mathematics Polynomials teacher for class 9 will help you to keep in touch with the topic thus reducing dependence on last minute studies
- You will be able to understand the type of questions which are expected in your Mathematics Polynomials class test
- You will be able to revise all topics given in the ebook for Class 9 Mathematics Polynomials as all questions have been provided in the question banks
- NCERT Class 9 Mathematics Polynomials Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
- Parents will be able to take print out of the assignments and give to their child easily.
All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 9 Mathematics Polynomials teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 9 Mathematics Polynomials Assignments PDF.

You can download free assignments for class 9 Mathematics Polynomials from https://www.assignmentsbag.com
You can get free PDF downloadable assignments for Grade 9 Mathematics Polynomials from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided assignments for all subjects in Grade 9, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge
Yes all test papers for Mathematics Polynomials Class 9 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.
https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.


