Please refer to the Systems of Particles and Rotational Motion Revision Notes given below. These revision notes have been designed as per the latest NCERT, CBSE and KVS books issued for the current academic year. Students will be able to understand the entire chapter in your class 11th Physics book. We have provided chapter wise Notes for Class 11 Physics as per the latest examination pattern.
Revision Notes Chapter 7 Systems of Particles and Rotational Motion
Students of Class 11 Physics will be able to revise the entire chapter and also learn all important concepts based on the topic wise notes given below. Our best teachers for Grade 11 have prepared these to help you get better marks in upcoming examinations. These revision notes cover all important topics given in this chapter.
CONCEPTS.
.Centre of mass of a body is a point where the entire mass of the body can be supposed to be concentrated
For a system of n-particles, the centre of mass is given by

Torque T The turning effect of a force with respect to some axis, is called moment of force or torque due to the force. Torque is measured as the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the axis of rotation.
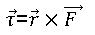
Angular momentum (L→). It is the rotational analogue of linear momentum and is measured as the product of linear momentum and the perpendicular distance of its line of axis of rotation.
Mathematically: If Ρ̅ is linear momentum of the particle and R→, its position vector, then
angular momentum of the particle,

(a) In Cartesian coordinates : Lz = xPy – YPx
(b) In polar coordinates : L = rp sin φ
Where is angle between the linear momentum vector Ρ̅ and the position of vector r¯
S.I unit of angular momentum is kg m2 s-1
Geometrically, angular momentum of a particle is equal to twice the product of mass of the particle and areal velocity of its radius vector about the given axis.
Relation between torque and angular momentum:

.Law of conservation of angular momentum. If no external torque acts on a system, then the total angular momentum of the system always remain conserved.

Moment of inertia (I). the moment of inertia of a rigid body about a given axis of rotation is the sum of the products of masses of the various particles and squares of their respective perpendicular distances from the axis of rotation.

SI unit of moment of inertia is kg m2
MI corresponding to mass of the body. However, it depends on shape & size of the body and also on position and configuration of the axis of rotation.
Radius of gyration (K). it is defined as the distance of a point from the axis of rotation at which, if whole mass of the body were concentrated, the moment of inertia of the body would be same as with the actual distribution of mass of the body.

SI unit of gyration is m. Note that the moment of inertia of a body about a given axis is equal to the product of mass of the body and squares of its radius of gyration about that axis i.e. I = M.
Theorem of perpendicular axes. It states that the moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moment of
inertia of the lamina about any two mutually perpendicular axes in its plane and intersecting each other at the point, where the perpendicular axis passes through the lamina.
Mathematically: lz = lx + lyI
Where x & y-axes lie in the plane of the Lamina and z-axis is perpendicular to its plane and passes through the point of intersecting of x and y axes.
Theorem of parallel axes. It states that the moment of inertia of a rigid body about any axis is equal to moment of inertia of the body about a parallel axis through its center of mass plus the product of mass of the body and the square of the perpendicular distance between the axes.
Mathematically: l = lc + Mh2 where lc is moment of inertia of the body about an axis through its centre of mass and is the perpendicular distance between the two axes.
Moment of inertia of a few bodies of regular shapes:
i. M.I. of a rod about an axis through its c.m. and perpendicular to rod, I = 1/12 ML
ii. M.I. of a circular ring about an axis through its centre and perpendicular to its plane, I = MR2
iii. M.I. of a circular disc about an axis through its centre and perpendicular to its plane, I = 1/2 MR
iv. M.I. of a right circular solid cylinder about its symmetry axis, = 1/2 MR2
v. M.I. of a right circular hollow cylinder about its axis = MR2
vi. M.I. of a solid sphere about its diameter, I = 1/5 MR2
vii. M.I. of spherical shell about its diameter, I = 1/3 MR2
.Moment of inertia and angular momentum. The moment of inertia of a rigid body about an axis is numerically equal to the angular momentum of the rigid body, when rotating with unit angular velocity about that axis.

Moment of inertia and kinetic energy of rotation. The moment of inertia of a rigid body about an axis of rotation is numerically equal to twice the kinetic energy of rotation of the body, when rotation with unit angular velocity about that axis.
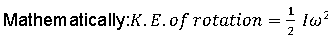
.Moment of inertia and torque. The moment of inertia of a rigid body about an axis of rotation is numerically equal to the external torque required to produce a unitangular acceleration in the body BOUT THE GIVEN AXIS.
MATHEMATICALLY:
Iw = constant vector,i.e., in magnitude, I1ω1 = I2ω2
provides no external torque acts on the system.
Law of conservation of angular momentum. If no external torque acts on a system, the total angular momentum of the system remains unchanged.
Mathematically:
For translational equilibrium of a rigid body,

For rotational equilibrium of a rigid body,

1. The following table gives a summary of the analogy between various quantities describing linear motion and rotational motion.





