We have provided CBSE Class 9 Mathematics Sample Paper with solutions below. These Sample guess papers have been prepared as per the latest examination guidelines and paper pattern issued by CBSE. Students of Class 9 should practice all practice papers for Class 9 Mathematics given below as it will help them top improve their understanding of the subject. Please click on the links below to access free sample paper for Mathematics Class 9.
Sample Papers for Class 9 Mathematics
CBSE Class 9 Mathematics Term 2 Sample Paper Set A
PART – A
Section – I
1. In a sample study of 600 people, it was found that 540 people have a high school certificate. If a person is selected at random, then the probability that the person has a high school certificate is
(a) 0.5
(b) 0.6
(c) 0.7
(d) 0.9
Answer
D
2. Zero of the polynomial p(z) = az + b – c ; z ≠ 0 is
(a) c − b/b
(b) c − b/a
(c) a − b/a
(d) b − a/c
Answer
B
3. The total surface area of a cube is 294 cm2, its each side is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 7 cm
Answer
D
4. If O is the centre of a circle, find the value of x in the following figure.
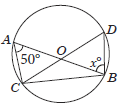
(a) 130°
(b) 40°
(c) 50°
(d) 60°
Answer
C
Section – II
Case study-based question is compulsory. Attempt any 4 sub parts. Each sub-part carries 1 mark.
5. A survey on few families of a particular society is done related to consumption of vegetarian or non-vegetarian food.

Total consumption is represented by a polynomial p(x) = x2 – 7x + 10. On the basis of given information, answer the following questions.
(i) Name the type of the given polynomial.
(a) Linear
(b) Quadratic
(c) Cubic
(d) Biquadratic
Answer
B
(ii) Write the sum of the coefficients of x2 and x in the given polynomial.
(a) 0
(b) 7
(c) –6
(d) 6
Answer
C
(iii) The value of the given polynomial at x = 1 is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
D
(iv) The value of the given polynomial at x = 2 is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
(v) Factorise the given polynomial.
(a) (x – 2) (x – 3)
(b) (x – 2) (x – 5)
(c) (x – 3) (x – 5)
(d) (x – 5) (x – 7)
Answer
B
PART – B
Section – III
6. Find the factors of x2 + 2x – 15.
Ans. We have, x2 + 2x – 15 = x2 + 5x – 3x – 15
= x(x + 5) – 3(x + 5) = (x + 5) (x – 3)
∴ Factors of x2 + 2x – 15 are (x + 5) and (x – 3).
7. Evaluate (without directly multiplying) : 205 × 195.
Ans. We have, 205 × 195 = (200 + 5) × (200 – 5)
= (200)2 – (5)2 = 40000 – 25 = 39975
8. If height and radius of a cone are h and r respectively and it is given that height of the cone is half the diameter of the base, then find the slant height of the cone.
Ans. We are given that,
Height (h) = Half of diameter of base of cone
⇒ h = 2r/2 ⇒ h = r
Now, slant height (l) = √h2 + r2 = √(r)2 + r2
= √2 r units.
OR
Find the volume of a right circular cylinder with radius 7 cm and height 10 cm.
Ans. Volume of cylinder = πr2h
= 22/7 × 7 ×7 × 10 = 1540 cm3
9. Can 110°, 80°, 70° and 95° be the angles of a quadrilateral? Why or why not?
Ans. We know that, sum of the angles of a quadrilateral is 360°.
Here, sum of the angles = 110° + 80° + 70° + 95°
= 355° ≠ 360°.
Therefore, these angles cannot be the angles of a quadrilateral.
10. Can an angle of 42.5° be constructed? Give reasons for your answer.
Ans. No, we cannot construct an angle of 42.5°
As 42.5° = 1/2 × 85° 2 85 and with the help of ruler and compass, we cannot construct and angle of 85°.
Section – IV
11. If one of the zeroes of the polynomial p(x) = 3x3 – 2x2 – mx + n is – 1, then find the value of m + n.
Ans. –1 is the zero of p(x) = 3x3 – 2x2 – mx + n
∴ p(–1) = 0
⇒ 3(–1)3 – 2(–1)2 – m(–1) + n = 0
⇒ –3 – 2 + m + n = 0 ⇒ m + n = 5
12. In the given figure, if PQRS is a parallelogram, then find the values of x and y.

Ans. In parallelogram PQRS,
SR || PQ and RP is a transversal.
∴ ∠SRP = ∠RPQ [Alternate interior angles]
⇒ 28° = 7y ⇒ y = 4°
Also, since PS || QR and PR is transversal
∴ ∠SPR = ∠PRQ [Alternate interior angles]
⇒ 8x = 32° ⇒ x = 4°
OR
In a DABC, D, E and F are the mid-points of BC, CA and AB respectively. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, find the perimeter of ΔDEF.
Ans.
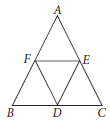
Since D, E and F are mid-points of BC, CA and AB respectively. Therefore by mid-point theorem, we have
DE = (1/2)AB = 3.5 cm,
EF = (1/2)BC = 4 cm and
DF = (1/2)AC = 4.5 cm
∴ Perimeter of DDEF = DE + EF + DF
= (3.5 + 4 + 4.5) cm = 12 cm
13. Three spheres of radii 3 cm, 4 cm and 5 cm are melted together to form a single sphere. Find the radius of new sphere.
Ans. Let radius of new sphere = r cm
According to question,
Volume of new sphere = Volume of the three spheres
⇒ 4/3 πr3 = 4/3 π(3)3 + 4/3 π(4)3 + 4/3 π(5)3
⇒ r3 = 27 + 64 + 125 = 216 = (6)3 ⇒ r = 6
Thus, radius of the new sphere = 6 cm
14. Draw perpendicular bisector of AB = 7.2 cm.
Ans. Steps of construction :
Step I : Draw a line segment AB = 7.2 cm by using graduated ruler.
Step II : Taking A as centre and radius more than half of length of AB, draw arcs on both side of line segment AB.
Step III : Taking B as centre and same radius as in Step II, draw arcs on both sides of AB, cutting the
previous arcs at E and F.
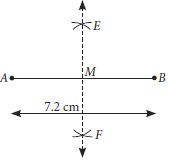
Step IV : Join EF, intersecting AB at M. Then, EF is the required perpendicular bisector of AB.
Section – V
15. Factorise :
(i) x2 + 9x + 18
(ii) 8p3 + 12/5 p2 + 6/25 p + 1/125
(iii) a3 − 2 2b3
Ans. (i) We have, x2 + 9x + 18 = x2 + 6x + 3x + 18
= x(x + 6) + 3(x + 6) = (x + 3) (x + 6)
(ii) We have, 8p3 + 12/5 p2 + 6/25 p + 1/125
= 8p3 +1/125 + 12/5p2 + 6/25p
= (2p)3 + (1/5)3 + 3(2p)2(1/5) + 3(2p)(1/5)2
= (2p + 1/5)3 [a3 + b3 + 3a2b + 3ab2 = (a + b)3]
= (2p + 1/5)(2p + 1/5)(2p + 1/5)
(iii) We have, a3 − 2√2b3 = (a)3 −(√2b)3
= (a − √2b)[a2 + a(√2b)+( 2b)2 ] [a3 – b3 = (a – b)(a2 + ab + b2)]
= (a − √2b)(a2 + √2ab + 2b2)
16. In the given figure, the two chords AC and BC are equal and the radius OC intersects AB at M. Then, find the ratio of AM and BM.

Ans. Given, AC = CB
⇒ ∠AOC = ∠BOC …(i)
[ Equal chords of a circle subtends equal angles at the centre]
In ΔAOM and ΔBOM, we have
∠AOM = ∠BOM [From (i)]
OA = OB [Radii of same circle]
OM = OM [Common]
∴ ΔAOM ≅ ΔBOM [By SAS congruency criteria]
Thus, AM = BM [By C.P.C.T.]
Hence, AM : BM = 1 : 1
OR
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90°.
Ans. Given : A circle is circumscribing a ΔABC whose centre is O.
To prove : ∠OBC + ∠BAC = 90°
Construction : Join BO and CO.
Proof : In DOBC, let ∠OBC = ∠OCB = θ [OB = OC = (Radii of same circle)] … (i)
∠BOC + ∠OCB + ∠CBO = 180° [By angle sum property of a triangle]
⇒ ∠BOC + θ + θ = 180° [Using (i)]
⇒ ∠BOC = 180° – 2θ … (ii)
Also, ∠BOC = 2∠BAC [ Angle subtended by an arc at the centre is twice the angle subtended by it at any point on the remaining part of the circle]
⇒ ∠BAC = 180° – 2θ/2 [Using (ii)]

⇒ ∠BAC = 90° – q
⇒ ∠BAC + q = 90°
∴ ∠BAC + ∠OBC = 90° [Using (i)]
17. A box contains 500 balls of the same shape and weight. Aman finds that, among the balls 160 balls are white, 200 are red and rest are black. What is the probability that a ball drawn at random from the box is (i) red (ii) not black?
Ans. Total number of balls = 500
Number of white balls = 160
Number of red balls = 200
(i) Probability that drawn ball is red = 200/500 =2/5
(ii) Now, number of black balls = 500 – (160 + 200) = 140
⇒ Number of non-black balls = 160 + 200 = 360
∴ Probability that drawn ball is non-black = 360/500 = 18/25
Section – VI
18. The internal and external diameters of a hollow hemispherical vessel are 21 cm and 24 cm respectively. The cost of painting one sq. cm of the surface is 14 paise. Find the total cost to paint the vessel all over. (Ignore the area of edge)
Ans. Let R cm and r cm be respectively the external and internal radii of the hemispherical vessel.
Then, R = 12 cm, r = 10.5 cm.
Now, internal surface area of the vessel = 2 × 22/7 x (10.5)2
External surface area of the vessel = 2 × 22/7 x (12)2
∴ Total area to be painted
= 2 × 22/7 x (10.5)2 + 2 × 22/7 x (12)2
= 2 × 22/7 x {(21/2)2 + (12)2 }
= 2 × 22/7 x (441/4+144) = 11187/7 cm2
Cost of painting at the rate of 14 paise per sq. cm
= Rs (11187 / 7 x 14/100) = Rs 223.74
OR
The radius and height of a cone are in the ratio 4 : 3. The area of the base is 154 cm2. Find the area of the curved surface area and total surface area of the cone.
Ans. Let radius and height of the cone be 4x and 3x respectively.
Now, Area of the base = 154 cm2 [Given]
⇒ πr2 = 154 ⇒ 22/7 × (4x)2 =154
⇒ x2 x 154 x 7/22 x 16 = 49/16 ⇒ x = √49/16 = 7/4 cm
∴ r = 4x = (4 x 7/4) cm = 7 cm
and h = (3 x 7/4) cm = 21/4 cm
Let the slant height be l cm. Then, l2 = r2 + h2
⇒ l = √r2 + h2 = √ 72 +(21/4)2 = 35/4 cm
∴ Curved surface area = πrl
= 22/7 × 7 × 35/4 = 192.5 cm2
Also, TSA = πr(r + l) = 22/7 × 7 (7 + 35/4) = 22 × 63/4 = 346.5 cm2
19. In the given figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that
∠P +∠Q = 1/2 (∠ABC + ∠ADC)

Ans. In DPBC, we have
∴ ∠P + ∠4 + ∠C = 180°
⇒ ∠P + 1/2∠ABC +∠C = 180° …(i)
In ΔQAD, we have
∠Q + ∠A + ∠1 = 180°
⇒ ∠Q + ∠A+ 1/2 ∠ADC = 180 ° …(ii)
Adding (i) and (ii), we get
∠P + ∠Q + ∠A+ ∠C + 1/2∠ABC + 1/2∠ADC = 180° + 180°
⇒ ∠P + ∠Q + ∠A+ ∠C + 1/2∠ABC + ∠ADC = 360°
But, ∠A + ∠ABC + ∠C + ∠ADC = 360° [Angle sum property of a quadrilateral]
∴ ∠P + ∠Q + ∠A+ ∠C + 1/2( ∠ABC + ∠ADC)
= ∠A + ∠ABC + ∠C + ∠ADC
⇒ ∠P + ∠Q = 1/2 (∠ABC + ∠ADC)
OR
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
Ans. Let ABCD be a square in which P, Q, R and S are the mid-points of side AB, BC, CD and DA respectively . Let us join AC and BD which bisect each other at O.

Since, ABCD is a square.
∴ AB = BC = CD = DA
Now, in DADC, S and R are mid-points of AD and DC respectively.
∴ SR || AC and SR = 1/2 AC …(i) [By mid-point theorem]
Similarly, in ΔABC,
PQ || AC and PQ = 1/2 AC …(ii)
From (i) and (ii), we have
SR || PQ and SR = (1/2)AC = PQ …(iii)
Similarly, SP || RQ and SP = (1/2)BD = RQ …(iv)
Also, AC = BD ….(v) [Diagonals of a square]
From (iii), (iv) and (v), we get
SR = PQ = SP = RQ
∴ PQRS is a parallelogram with all its sides of equal length. …(vi)
Let F be point where BD intersects SR and E be the point where AC intersects QR.
Now, in quadrilateral OERF, OE || FR and OF || ER
∴ OERF is a parallelogram.
⇒ ∠ERF = ∠EOF [Opposite angles of a parallelogram]
But ∠EOF = 90° [Diagonals of a square bisect each other at right angles]
∴ ∠ERF = 90° …(vii)
Now, from (vi) and (vii), we have
PQRS is a parallelogram with one of its angle as right angle.
∴ PQRS is a square.
Thus, a quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.

