We have provided CBSE Class 12 Mathematics Sample Paper with solutions below. These Sample guess papers have been prepared as per the latest examination guidelines and paper pattern issued by CBSE. Students of Class 12 should practice all practice papers for Class 12 Mathematics given below as it will help them top improve their understanding of the subject. Please click on the links below to access free sample paper for Mathematics Class 12.
Sample Papers for Class 12 Mathematics
CBSE Class 12 Mathematics Term 1 Sample Paper Set A
SECTION-A
In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.
1. sin [π/r – sin-4(-1/2)] is equal to :
(A) 1/2
(B) 1/3
(C) –1
(D) 1
Answer
D
2. The value of k (k < 0) for which the function f defined as
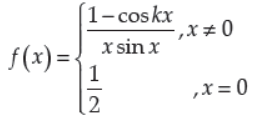
is continuous at x = 0 is :
(A) ± 1
(B) –1
(C) ± 1/2
(D) 1/2
Answer
B
3. If A = [aij] is a square matrix of order 2 such that aij =
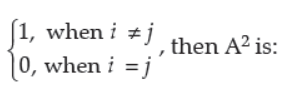

Answer
D
4. Value of k, for which A =

is a singular matrix is:
(A) 4
(B) –4
(C) ±4
(D) 0
Answer
C
5. Find the intervals in which the function f given by f(x) = x2 – 4x + 6 is strictly increasing:
(A) (– ∞, 2) ∪ (2, ∞)
(B) (2, ∞)
(C) (− ∞, 2)
(D) (– ∞, 2] ∪ (2, ∞)
Answer
B
6. Given that A is a square matrix of order 3 and | A | = – 4, then | adj A | is equal to:
(A) –4
(B) 4
(C) –16
(D) 16
Answer
D
7. A relation R in set A = {1, 2, 3} is defined as R = {(1, 1), (1, 2), (2, 2), (3, 3)}. Which of the following ordered pair in R shall be removed to make it an equivalence relation in A?
(A) (1, 1)
(B) (1, 2)
(C) (2, 2)
(D) (3, 3)
Answer
B
8. If

,then value of a + b – c + 2d is:
(A) 8
(B) 10
(C) 4
(D) –8
Answer
A
9. The point at which the normal to the curve y = x + 1/x , x >0 is perpendicular to the line 3x – 4y – 7 = 0 is:
(A) (2, 5/2)
(B) (±2, 5/2)
(C) (–1/2, 5/2)
(D) (1/2, 5/2)
Answer
A
10. sin (tan–1x), where |x| < 1, is equal to:
(A) x/√1- x2
(B) 1/√1-x2
(C) 1/√1+x2
(D) x/√1+x2
Answer
D
11. Let the relation R in the set A = {x Î Z : 0 £ x £ 12}, given by R = {(a, b) : |a – b| is a multiple of 4}. Then [1], the equivalence class containing 1, is:
(A) {1, 5, 9}
(B) {0, 1, 2, 5}
(C) Φ
(D) A
Answer
A
12. If ex + ey = ex+y, then dy/dx is:
(A) ey – x
(B) ex + y
(C) –ey – x
(D) 2ex – y
Answer
C
13. Given that matrices A and B are of order 3 × n and m × 5 respectively, then the order of matrix C = 5A + 3B is:
(A) 3 × 5 and m = n
(B) 3 × 5
(C) 3 × 3
(D) 5 × 5
Answer
B
14. If y = 5 cos x – 3 sin x, then d2y/dx2 is equal to:
(A) –y
(B) y
(C) 25y
(D) 9y
Answer
A
15. For matrix A =
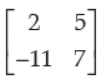
,(adj A)’ is equal to:

Answer
C
16. The points on the curve x2/9 + y2/16 = 1 at which the tangents are parallel to y-axis are:
(A) (0, ±4)
(B) (±4, 0)
(C) (±3, 0)
(D) (0, ±3)
Answer
C
17. Given that A = [aij] is a square matrix of order 3 × 3 and |A| = −7, then the value of 3∑i=1 a12 A12 , where Aij denotes the cofactor of element aij is:
(A) 7
(B) –7
(C) 0
(D) 49
Answer
B
18. If y = log(cos ex), then dy/dx is:
(A) cos ex−1
(B) e–x cos ex
(C) ex sin ex
(D) –ex tan ex
Answer
D
19. Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
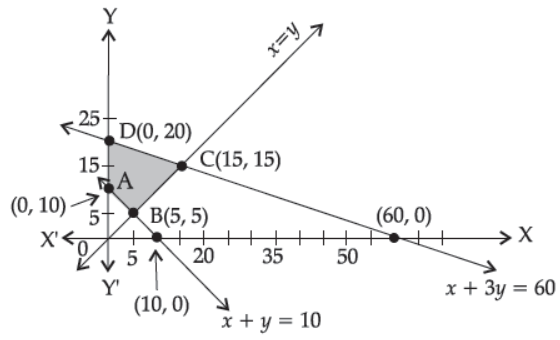
(A) Point B
(B) Point C
(C) Point D
(D) every point on the line segment CD
Answer
D
20. The least value of the function f(x) = 2cos x + x in the closed interval [0,π/2] is:
(A) 2
(B) π/6 + √3
(C) π/2
(D) The least value does not exist
Answer
C
SECTION-B
In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.
21. The function f : R → R defined as f(x) = x3 is:
(A) One-one but not onto
(B) Not one-one but onto
(C) Neither one-one nor onto
(D) One-one and onto
Answer
D
22. If x = a sec q, y = b tan q, then d2y/dx2 at θ = π/6 is:
(A) -3√3b/a2
(B) -2√3b/a
(C) -3√3b/a
(D) -b/3√3 a2
Answer
A
23. In the given graph, the feasible region for a LPP is shaded. The objective function Z = 2x – 3y, will be minimum at:

(A) (4, 10)
(B) (6, 8)
(C) (0, 8)
(D) (6, 5)
Answer
C
24. The derivative of sin–1 (2x√1-x2) w.r.t sin–1x, 1/√ < x < 1, is:
(A) 2
(B) π/2 – 2
(C) π/2
(D) –2
Answer
A
25. If A =
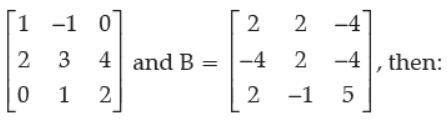
(A) A–1 = B
(B) A–1 = 6B
(C) B–1 = B
(D) B–1 = 1/6 A
Answer
D
26. The real function f(x) = 2×3 – 3×2 – 36x + 7 is:
(A) Strictly increasing in (− ∞,−2) and strictly decreasing in ( −2, ∞)
(B) Strictly decreasing in ( −2, 3)
(C) Strictly decreasing in (− ∞, 3) and strictly increasing in (3, ∞)
(D) Strictly decreasing in (− ∞, −2) ∪ (3, ∞)
Answer
B
27. Simplest form of tan-1 (√1+cose x +√1-cos x/√1+cose x – √1-cos x) , π < x < 3π /2 is:
(A) π/4 – x/2
(B) 3π/2 – x/2
(C) -x/2
(D) π – x/2
Answer
A
28. Given that A is a non-singular matrix of order 3 such that A2 = 2A, then value of |2A| is:
(A) 6
(B) 8
(C) 64
(D) 16
Answer
C
29. The value of b for which the function f(x) = x + cosx + b is strictly decreasing over R is:
(A) b < 1
(B) No value of b exists
(C) b ≤ 1
(D) b ≥ 1
Answer
B
30. Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}, then:
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
Answer
C
31. The point(s), at which the function f given by f(x) =

is continuous, is/are:
(A) x ∈ R
(B) x = 0
(C) x ∈ R –{0}
(D) x = –1 and 1
Answer
A
32. If A =

, then the values of k, a and b respectively are:
(A) −6, −12, −18
(B) −6, −4, −9
(C) −6, 4, 9
(D) −6, 12, 18
Answer
B
33. A linear programming problem is as follows:
Minimize Z = 30x + 50y
subject to the constraints,
3x + 5y ≥15
2x + 3y ≤ 18
x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at
(A) a unique point
(B) no point
(C) infinitely many points
(D) two points only
Answer
D
34. The area of a trapezium is defined by function f and given by f(x) = (10 + x) √100 – x2 , then the area when it is maximised is:
(A) 75 cm2
(B) 7 √3 cm2
(C) 75 √3 cm2
(D) 5 cm2
Answer
C
35. If A is square matrix such that A2 = A, then (I + A)³ – 7 A is equal to:
(A) A
(B) I + A
(C) I − A
(D) I
Answer
D
36. If tan–1 x = y, then:
(A) −1< y <1
(B) -π/2 ≤ y ≤ π/2
(C) -π/2 < y < π/2
(D) y ∈ {-π/2 , π/2}
Answer
C
37. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Based on the given information, f is best defined as:
(A) Surjective function
(B) Injective function
(C) Bijective function
(D) function
Answer
B
38. For A =
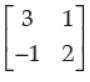
,then 14A–1 is given by:

Answer
B
39. The point(s) on the curve y = x3 – 11x + 5 at which the tangent is y = x – 11 is/are:
(A) (–2, 19)
(B) (2, – 9)
(C) (±2, 19)
(D) (–2, 19) and (2, – 9)
Answer
B
40. Given that A =
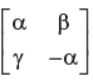
and A2 = 3I, then:
(A) 1 + α2 + βϒ = 0
(B) 1 – α2 – βϒ = 0
(C) 3 – α2 – βϒ = 0
(D) 3 + α2 + βϒ = 0
Answer
C
SECTION-C
In this section, attempt any 8 questions. Each question is of 1-mark weightage.
Questions 46-50 are based on a Case-Study.
41. For an objective function Z = ax + by, where a, b > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
(A) b − 3a = 0
(B) a = 3b
(C) a + 2b = 0
(D) 2a − b = 0
Answer
A
42. For which value of m is the line y = mx + 1 a tangent to the curve y2 = 4x?
(A) 1/2
(B) 1
(C) 2
(D) 3
Answer
B
43. The maximum value of [x(x-1)+1]1/3 , 0 ≤ x ≤ 1 is:
(A) 0
(B) 1/2
(C) 1
(D) 3√1/3
Answer
C
44. In a linear programming problem, the constraints on the decision variables x and y are x − 3y ≥ 0, y ≥ 0, 0 ≤ x ≤ 3. The feasible region
(A) is not in the first quadrant
(B) is bounded in the first quadrant
(C) is unbounded in the first quadrant
(D) does not exist
Answer
B
45. Let A =

, where 0 ≤ a ≤ 2p, then:
(A) |A|= 0
(B) |A| ∈ (2, ∞)
(C) |A| ∈ (2, 4)
(D) |A| ∈ [2, 4]
Answer
D
CASE-STUDY
The fuel cost per hour for running a train is proportional to the square of the speed it generates in km per hour. If the fuel costs `48 per hour at speed 16 km per hour and the fixed charges to run the train amount to `1200 per hour.
Assume the speed of the train as v km/h.
Based on the given information, answer the following questions.

46. Given that the fuel cost per hour is k times the square of the speed the train generates in km/h, the value of k is:
(A) 16/3
(B) 1/3
(C) 3
(D) 3/16
Answer
D
47. If the train has travelled a distance of 500km, then the total cost of running the train is given by function:
(A) 15/16 v + 600000/v
(B) 75/4 v + 600000/v
(C) 5/16 v2 + 150000/v
(D) 3/16 v + 6000/v
Answer
B
48. The most economical speed to run the train is:
(A) 18km/h
(B) 5km/h
(C) 80km/h
(D) 40km/h
Answer
C
49. The fuel cost for the train to travel 500 km at the most economical speed is:
(A) ₹3750
(B) ₹750
(C) ₹7500
(D) ₹75000
Answer
C
50. The total cost of the train to travel 500km at the most economical speed is:
(A) ₹3750
(B) ₹75000
(C) ₹7500
(D) ₹15000
Answer
D
