See below CBSE Class 12 Mathematics Sample Paper Set C with solutions. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern issued by CBSE for the current academic year. All sample papers provided by our Class 12 Mathematics teachers are with answers. You can see the sample paper given below and use them for more practice for Class 12 Mathematics examination.
1. All possible two factors products are formed from the numbers 1, 2, 3, 4, ….., 200. The number of factors out of total obtained which are multiples of 5 is
(a) 5040
(b) 7180
(c) 8150
(d) None
Answer
B
2. If z be a complex number satisfying z4 + z3 + 2z2 + z + 1 = 0 then |z| is equal to
(a) 1/2
(b) 3/4
(c) 1
(d) No unique value
Answer
C
3. The number of real solutions of the equation sin(ex)= 5x + 5−x is
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
A
4. The equation 2cos2x/2sin2x = x2 + 1/x2 , 0 ≤ x ≤ π/2 has
(a) one real solution
(b) no real solution
(c) more than one real solution
(d) none of these
Answer
B
5. If log a, log b, and log c are in A.P. and also log a – log 2b, log 2b – log 3c, log 3c – log a are in A.P., then :
(a) a, b, c, are in H.P.
(b) a, 2b, 3c are in A.P.
(c) a, b, c are the sides of a triangle
(d) none of the above
Answer
C
6. Which of the following is correct ?
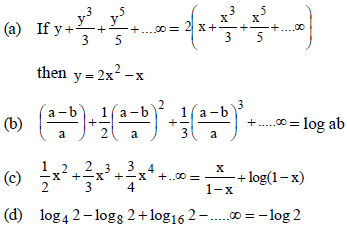
Answer
C
7. Incorrect sum from the following is :
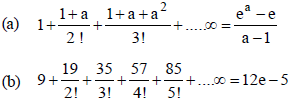

Answer
C
8. The value of the determinant
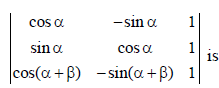
(a) independent of α
(b) independent of β
(c) independent of α & β
(d) None of these
Answer
A
9. The number of solution of the equation
tan 3x = sin 6x in [0,π/6] ∪ (π/6,π/2) is :
(a) 5
(b) 4
(c) 3
(d) 1
Answer
A
10. If sin−1 x + sin−1y + sin−1z = 3π/2 then the value of x100+ y100+ z100− 3/x101+ y101+ z101 is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
C
11. If A and B are positive acute angles satisfying 3cos2 A + 2cos2 B = 4 and 3sin A/sin B = 2cos B/cos A Then the value of A + 2B is equal to :
(a) π/6
(b) π/2
(c) π/3
(d) π/4
Answer
B
12. If α = sin−1√3/2 + sin−11/3
and β = cos−1√3/2 + cos−11/3 , then :
(a) α < β
(b) α = β
(c) α > β
(d) α +β = 2π
Answer
A
13. The principal value of cos–1 (– sin 7π/6) is
(a) 5π/3
(b) 7π/6
(c) π/3
(d) None
Answer
C
14. If α,β, γ are the altitudes of a triangle, then α−1 + β−1 + γ−1 =
(a) Δ / s
(b) s / Δ
(c) sD
(d) s / Δ2
Answer
B
15. A harbour lies in a direction 60° south of west from a fort and at a distance 30 km from it, a ship sets out from the harbour at noon and sails due east at 10 km an hour. The ship will be 70 km from the fort at :
(a) 7 p.m.
(b) 8 p.m.
(c) 5 p.m.
(d) 10 p.m.
Answer
B
16. The points with co-ordinates (2a, 3a), (3b, 2b) and (c, c) are collinear
(a) for no value of a, b, c
(b) for all values of a, b, c
(c) iff a, c/5, b are in H.P.
(d) iff a, 2c/5, b are in H.P.
Answer
D
17. The equation of the pair of straight lines parallel to the y-axis and which are tangents to the circle
x2 + y2 −6x−4y−12=0 is
(a) x2 − 4y − 21 = 0
(b) x2 − 5x + 6 = 0
(c) x2 − 6x −16 = 0
(d) None of these
Answer
C
18. The length of the chord x + y = 3 intercepted by the circle x2 + y2 − 2x − 2y − 2 = 0 is
(a) 7/2
(b) 3√3/2
(c) √14
(d) √7/2
Answer
C
19. If the eccentricity of the hyperbola x2 – y2 coces2 α = 25 is 5 times the eccentricity of the ellipse x2 cosec2α + y2 = 5, then α is equal to :

Answer
A
20. The point of intersection of the tangents to the parabola y2 = 4ax at the points ‘t1‘ and ‘t2‘ is
(a) (at1t2, a(t1 + t2))
(b) (at1t2, at1t2(t1 + t2))
(c) (at1t2 (t1 + t2), a (t1 + t2)
(d) None of these
Answer
A
21. Four distinct points (2k, 3k), (1, 0), (0, 1) and (0, 0) lie on circle for
(a) all integral values of k
(b) 0 < k < 1
(c) k < 0
(d) For one value of k
Answer
D
22. The condition that the straight line cx − by + b2 = 0 may touch the circle x2 + y2 = ax + by , is
(a) abc = 1
(b) a = c
(c) b = ac
(d) None of these
Answer
B
23. If f(x) = cos[π2] x + cos [–π2]x, where [x] stands for the greatest integer function, then
(a) f(π/2) = −1
(b) f (π) = 1
(c) f (−π) = 1
(d) f(π/4) = 2
Answer
A
24. Let f ”(x) be continuous at x = 0 and f ” (0) = 4.
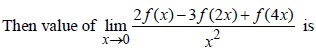
(a) 12
(b) 10
(c) 6
(d) 4
Answer
A
25. If xpyq = (x + y)p+q, then dy/dx is equal to
(a) y/x
(b) py/qx
(c) x/y
(d) qy/px
Answer
A
26. Let f(x) = xn, n being a non-negative integer. The value of n for which equality
f ‘ (a + b) = f ‘ (a) + f ‘ (b) is valid for all a, b > 0 is :
(a) 5
(b) 1
(c) 2
(d) 4
Answer
C
27. The angle at which the curve y = kekx intersects the y-axis is :

Answer
B
28. The maximum value of the function
y = a2/x + b2/a−x , a > 0, b > 0 in (0, a) is :
(a) a + b
(b) 1/a + b
(c) 1/a (a + b)2
(d) 1/a2(a + b)
Answer
C
29. The set of all points, where the function f (x) = x/(1 + | x |) is differentiable, is
(a) (–¥, ¥)
(b) (0, ¥)
(c) (–¥, 0) È (0,¥)
(d) none of these
Answer
A
30. If y = sin −1 x + cos −1 √(1− x2 ), then dy/dx at x = –1 /√2 , is
(a) 0
(b) 2
(c) does not exist
(d) none of these.
Answer
A
31.
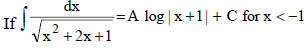
then A is
(a) 0
(b) 1
(c) –1
(d) None of these
Answer
C
32.
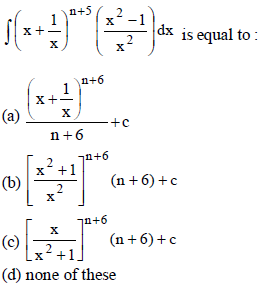
Answer
A
33.
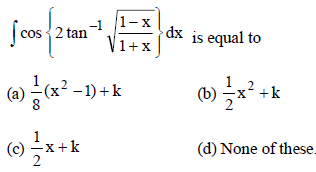
Answer
B
34.

(a) π/4
(b) π2/4
(c) π/2
(d) π2/2
Answer
B
35.
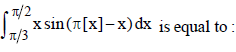
(a) 1/2 + π/6
(b) 1 − √3/2 + π/6
(c) −1/2 − π/6
(d) √3/2 − 1 − π/6
Answer
B
36. The solution to the differential equation
dy/dx = e3x − 2y x2e − 2y is
(a) e2y = e3x + x3 + C
(b) 3e2y = 2(e3x + x3) + c
(c) e3x+2y = x3 + c
(d) none of these.
Answer
B
37. The solution of the differential equation
(xy2 + x)dx + (yx2 + y)dy = 0 is
(a) (x2 +1)(y2 +1) = c
(b) ex2 + ey2 = c
(c) (y2 +1) = c(x2 +1)
(d) none of these.
Answer
A
38.
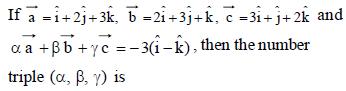
(a) (2, –1, –1)
(b) (–2, 1, 1)
(c) (–2, –1, 1)
(d) (2, 1, –1)
Answer
A
39. For any vector P¯ , the value of
3/2{|P¯ × î|2 + |P¯ × j|2 +|P¯ × k^|2 is
(a) P¯2
(b) 2P¯2
(c) 3P¯2
(d) 4P¯2
Answer
C
40. The position vector of A and B are
2î + 2j + k^ and 2î + 4j + 4k^
The length of the internal bisector of ∠BOA of triangle AOB is

Answer
B
41. If α,β,γ are the angles which a half ray makes with the positive directions of the axes, then sin2 α + sin2 β + sin2 γ is equal to
(a) 1
(b) 2
(c) 0
(d) –1.
Answer
B
42. The shortest distance from the point (1, 2, –1) to the surface of the sphere x2 + y2 + z2 = 24 is
(a) 3√6
(b) 2√6
(c) √6
(d) 12
Answer
C
43. If the probability that A and B will die within a year are p and q respectively, then the probability that only one of them will be alive at the end of the year is
(a) p + q
(b) p + q – 2pq
(c) p + q – pq
(d) p + q + pq.
Answer
B
44. Let u¯ , v¯ and w¯ be vectors such that u¯ + v¯ + w¯ = 0¯ .
If | u¯ |= 3, | v¯ |= 4 and | w¯ |= 5 , then
u¯ . v¯ + v¯ . w¯ + w¯ . u¯ is
(a) 47
(b) –25
(c) 0
(d) 25
Answer
B
45. A rectangular parallelopiped is formed by drawing planes through the points (–1, 2, 5) and (1, –1, –1) and parallel to the coordinate planes. The length of the diagonal of the parallelopiped is
(a) 2
(b) 3
(c) 6
(d) 7
Answer
D
