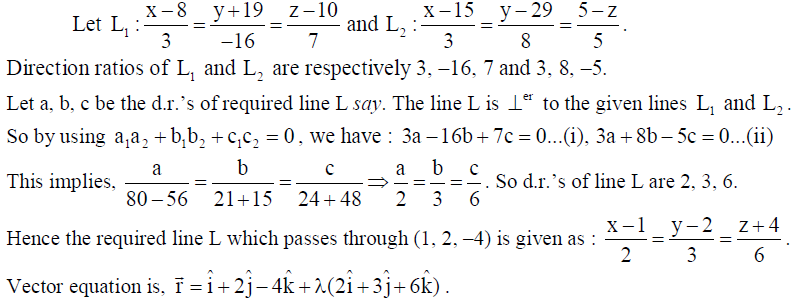See below CBSE Class 12 Mathematics Sample Paper Set K with solutions. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern issued by CBSE for the current academic year. All sample papers provided by our Class 12 Mathematics teachers are with answers. You can see the sample paper given below and use them for more practice for Class 12 Mathematics examination.
SECTION – A
1. If A is a 3×3 invertible matrix, then what will be the value of k if det(A-1) = (detA)k .
Solution: As | A-1 | = |A |-1 ∴ k = -1.
2. Determine the value of the constant ‘k’ so that f(x) =
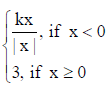
is continuous at x = 0 .
Solution:
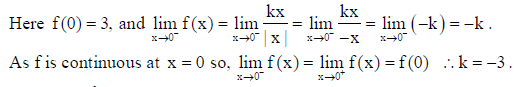
3. Evaluate :
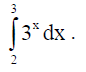
Solution:
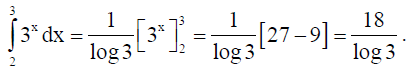
4. If a line makes angles 90o and 60o respectively with the positive direction of x and y axes, find the angle which it makes with the positive direction of z-axis.
Solution: Let the line is inclined at an angle of ϒ with positive direction of z-axis.
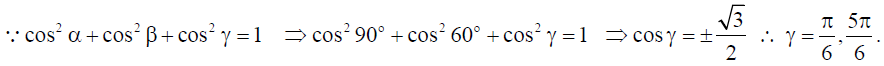
SECTION – B
5. Show that all the diagonal elements of a skew symmetric matrix are zero.
Solution: Let A = [aij] be a square matrix such that it is skew-symmetric. So, A = -AT
That is, [aij] = -[aij] .
For its diagonal elements, we have [aij] = -[aii] which implies, 2[aii] = O (Replacing j by i).
⇒ [aii] = [0] ∴ aii = 0 . Hence all the diagonal elements if a skew symmetric matrix are zero.
6. Find dy/dx at x = 1 , y = π/4 if sin2 y + cos xy = K .
Solution: Here sin2 y + cos xy = K ⇒ sin2y dy/dx – sin xy(x dy/dx + y) = 0
⇒ (sin2y – x sin xy)dy/dx = y sin xy ⇒ dy/dx = y sin xy/sin 2y – x sin xy

7. The volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm.
Solution:
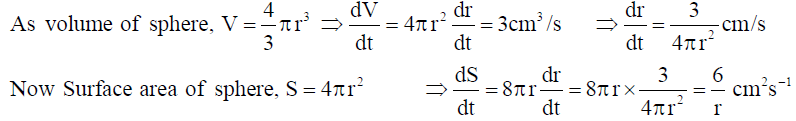
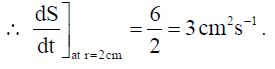
8. Show that the function f (x) = 4x3 – 18x2 + 27x – 7 is always increasing on R.
Solution: Here f (x) = 4x3 -18x2 + 27x – 7 ⇒ f ‘(x) = 12x2 – 36x + 27 = 3(4x2 – 12x + 9)
⇒ f ‘(x) = 3(2x – 3)2 ≥ 0 for all x ∈ R ∴ f (x) is always increasing on R.
# Note that f (x) is strictly increasing for all Real values of x except 3/2.
9. Find the vector equation of the line passing through the points A(1, 2, –1) and parallel to the line 5x – 25 = 14 – 7y = 35z .
Solution: Given line can be rewritten as x-5/1/5 = y-2/-1/7 = z/1/35 i.e., x-5/7 = y-2/-5 = z/1 . So the d.r.’s of the this line and any line parallel to the given line shall be proportional to 7, –5, 1.
Hence the required line through given point is : x-1/7 = y-2/-5 = z+1/1 .
Vector eq. is : r̅ = î + 2ĵ – k̂+ λ(7î – 5ĵ + k̂) .
10. Prove that if E and F are independent events, then the events E and F’ are also independent.
Solution:

Hence the events E and F’ are also independent events.
11. A small firm manufactures necklace and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a bracelet is ₹ 300 and that on a necklace is ₹ 100. Formulate an L.P.P. for finding how many of each should be produced daily to maximize the profit. It is being given that at least one of each must be produced.
Solution: Let the number of necklace and bracelets made per day be x and y respectively.
To maximize: Z = ₹ (100x + 300y)
Subject to constraints: x + y ≤ 24, x + 2y ≤ 32, x ≥ 1, y ≥1; x, y ≥ 0
i.e., x + y ≤ 24, x + 2y ≤ 32, x ≥1, y ≥1.
12. Find
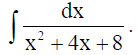
Solution:
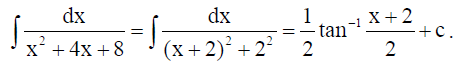
13. Prove that : tan{π/4 + 1/2 cos-1 a/b} + tan{π/4 – 1/2 cos-1 a/b} = 2b/a .
Solution: Consider LHS and put θ = 1/2 cos-1 a/b ⇒ cos2 θ = a/b …(i)
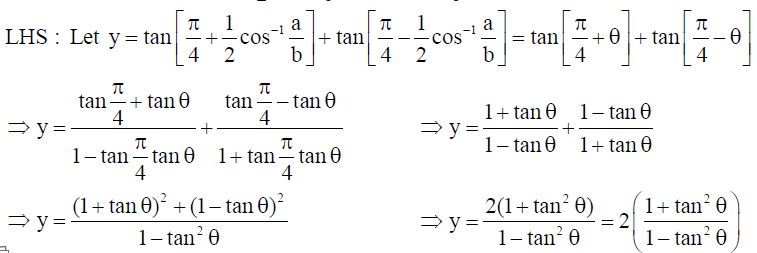

14. Using properties of determinants, prove that
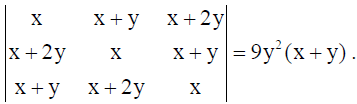
Solution:
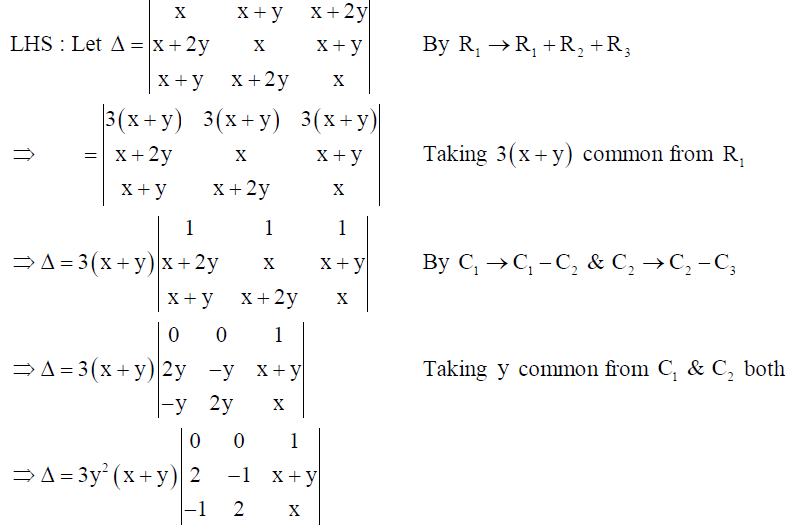
OR
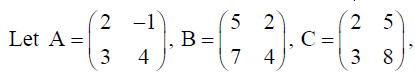
find a matrix D such that CD-AB = O .
Solution:

15. Differentiate the function (sin x)x + sin-1 √x with respect to x.
Solution:
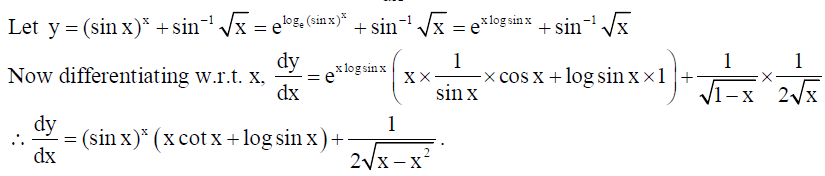
OR
If xmyn = (x + y)m+n , prove that d2y/dx2 = 0 .
Solution:
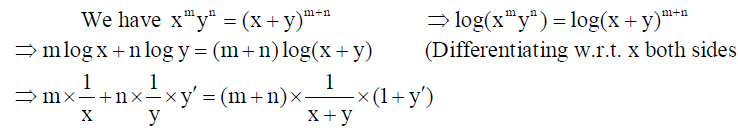
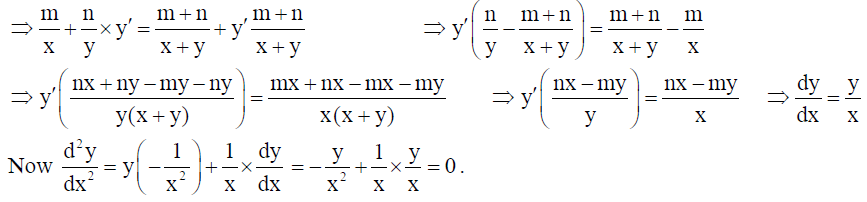
16. Find
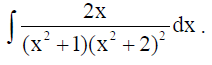
Solution:
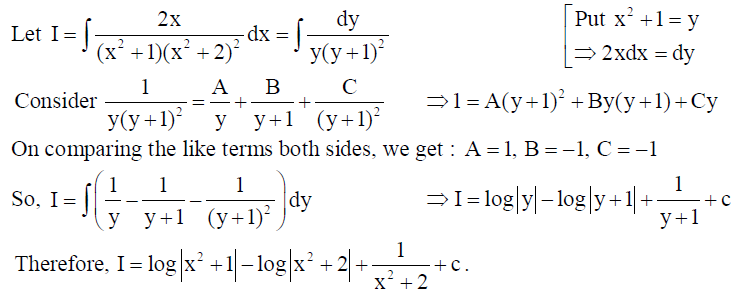
17. Evaluate :
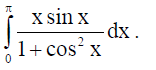
Solution:

OR
Evaluate :
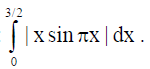
Solution:
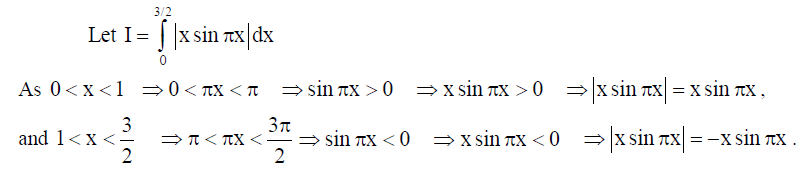
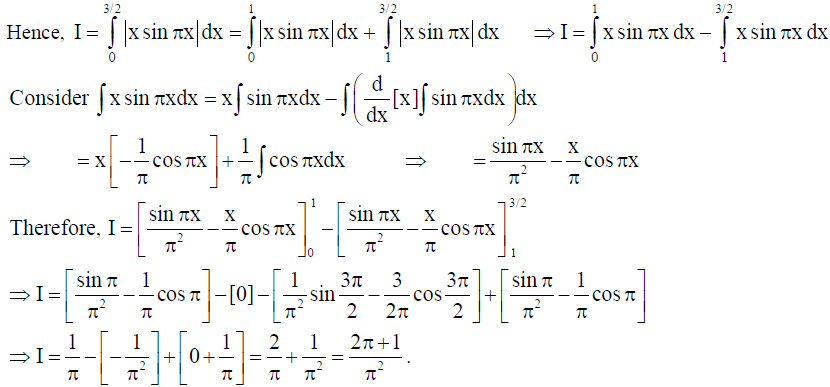
18. Prove that x2 – y2 = c(x2 + y2 )2 is the general solution of the differential equation (x3 – 3xy2 )dx = (y3 – 3x2y)dy, where c is a parameter.
Solution: Given (x3 – 3xy2 )dx – (y3 – 3x2y)dy = 0 ⇒ (y3 – 3x2y)dy = (x3 – 3xy2 )dx

19. Let a̅ = î + ĵ + k̂, b̅ = î and c̅ = c1î + c2ĵ + c3k̂, then
(a) Let c1 = 1 and c2 = 2 , find c3 , which makes a̅ , b̅ and c̅ coplanar.
Solution:


20. If a̅ , b̅ and c̅ are mutually perpendicular vectors of equal magnitudes, show that the vector a̅ + b̅ + c̅ is equally inclined to a̅ , b̅ and c̅ . Also, find the angle which a̅ + b̅ + c̅ makes with a̅ or b̅ or c̅ .
Solution:

21. The random variable X can take only the values 0, 1, 2, 3. Given that P(X = 0) = P(X = 1) = p, P(X = 2) = P(X = 3) such that

Solution:
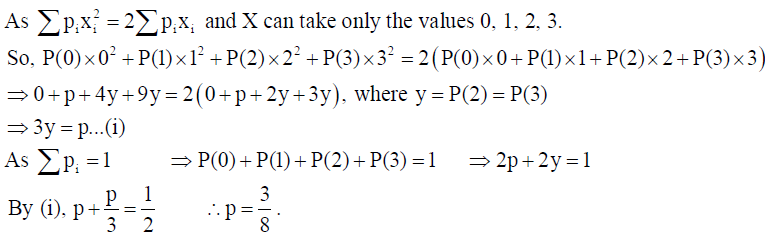
22. Often it is taken that a truthful person commands more respect in the society. A man is known to speak the truth 4 out of 5 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
Do you also agree that the value of truthfulness leads to more respect in the society?
Solution: Let A : the man reports that six occurs, E : six actually occurs.
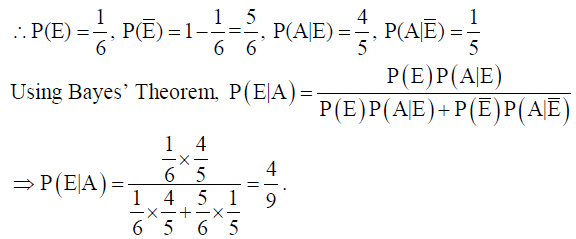
Yes, we agree that the value of truthfulness leads to more respect in the society as a person speaking truth is more reliable.
23. Solve the following L.P.P. graphically :
Minimize : S = 5x +10y
Subject to : x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solution: To Minimize : S = 5x + 10y
Subject to : x + 2y ≤ 120, x + y ≥ 60,
x – 2y ≥ 0, x ≥ 0, y ≥ 0 .
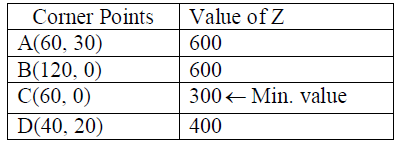

Clearly, Minimum value of S = 300 at C(60,0) .
SECTION – D
24. Use product
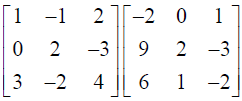
to solve the system of equations x + 3z = 9, -x + 2y – 2z = 4 , 2x – 3y + 4z = -3 .
Solution:
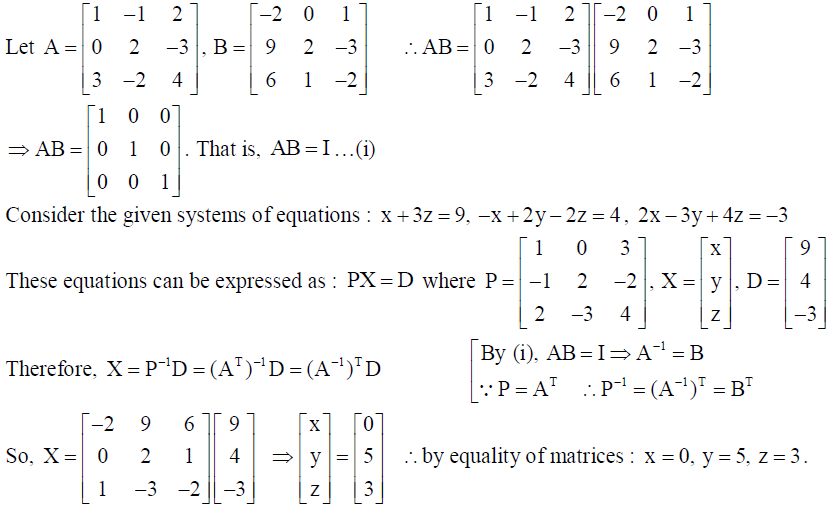
25. Consider f :R [ 5,∞) given by f (x) 9x2 + 6x – 5 . Show that f is invertible with f-1(y) = ( √y+6-1/3).
Hence find (i) f-1(10) (ii) y if f-1(y) = 4/3.
Solution: Let y be an arbitrary element of range of function i.e., y ε S, where S = [-5,∞) .
Then y = 9x2 + 6x – 5, for some x ε R , which implies that y = (3x + 1)2 – 6 .
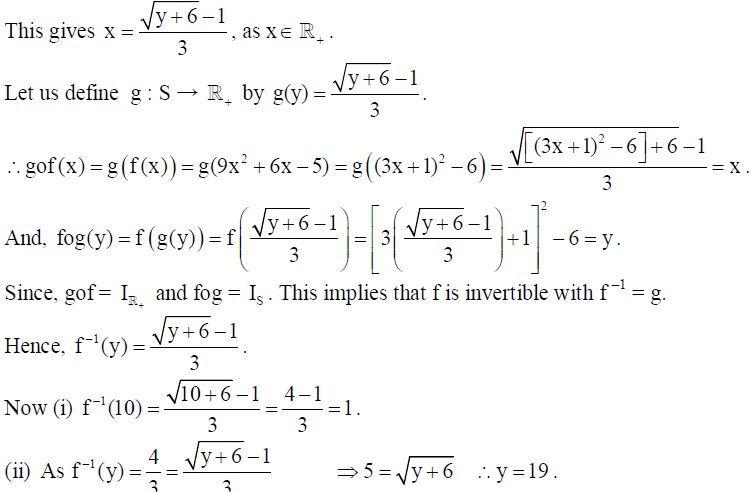
OR
Discuss the commutativity and associativity of binary operation ‘*’ defined on
A = Q-{1} by the rule a *b = a – b + ab for all a, b ε A. Also find the identity element of * in A and hence find the invertible elements of A.
Solution: Here a *b = a – b + ab for all a, b ε A where A = Q-{1}.
Commutativity : As b*a = b – a + ba ≠ a *b so, * isn’t commutative.
Associativity : Let a, b,c ε A.
(a *b)*c = (a – b + ab)*c = a – b + ab – c + ac – bc + abc…(i)
Also, a *(b*c) = a *(b – c + bc) = a – b + c – bc + ab – ac + abc…(ii)
By (i) and (ii), we can say that * isn’t associative.
Let e be the identity element.
So, a *e = e*a = a .
When a *e = a ⇒ a – e + ae = a =e = 0
When e*a = a ⇒ e – a + ea = a ⇒ e = 2a/1+a
Since e is not unique therefore, there’s no identity element for * in A.
As there is no identity element so, inverse doesn’t exist too.
NOTE that * is not binary here. Let’s see how! Assume that a, bεA = Q-{1}.
If we take a = 0, b = -1 then, 0*(-1) = 0 – (-1) + 0(-1) =1 ε A. That is, a *bεA ∀ a, bεA .
Hence * is not binary operation.
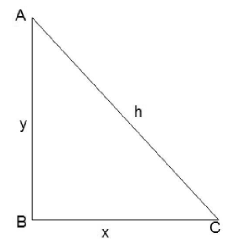
26. If the sum of the lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum, when the angle between them is π/3 .
Solution: Let x + h = S (given)…(i)
Let ∠ACB = θ .
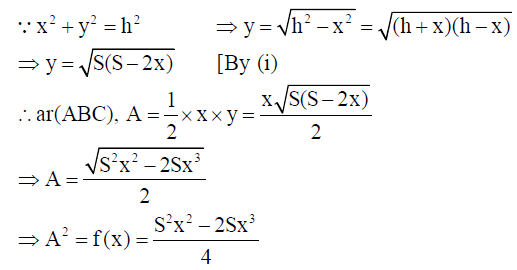

27. Using integration, find the area of region bounded by the triangle whose vertices are (–2, 1), (0,4) and (2, 3).
Solution: Let A(–2, 1), B(0, 4) and C(2, 3).
Eq. of AB, BC and CA are respectively :

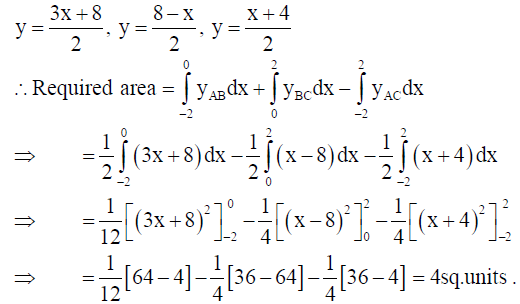
OR
Find the area bounded by the circle x2 + y2 = 16 and the line √3y = x in the I quadrant, using integration.
Solution:

NOTE that in the question paper, it is not mentioned which area is to be found – with the x axis or with the y axis.
28. Solve the differential equation x dy/dx + y = x cos x + sin x , given that y 1 when x = π/2.
Solution: Given differential equation can be rewritten as dy/dx + y/x = cos x + sin x /x .
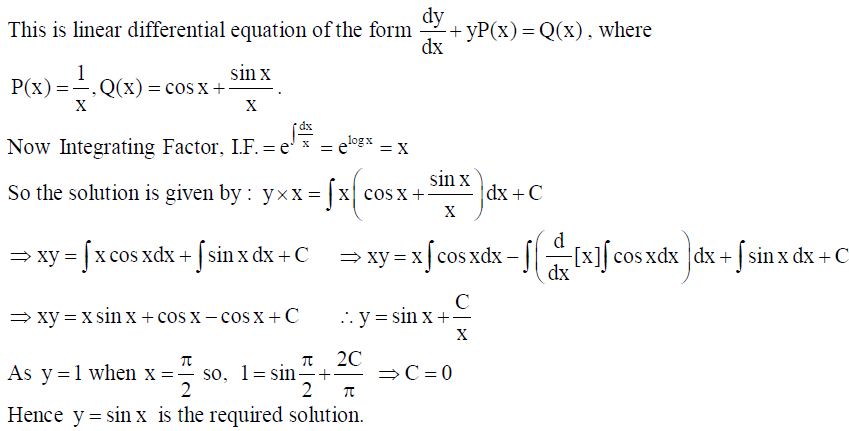
29. Find the equation of the plane through the line of intersection of the planes r̅.(2î – 3ĵ 4k̂ ) =1 and r̅.(î – ˆj) + 4 = 0 and perpendicular to the plane r̅.(2î – ĵ k̂) + 8 = 0 . Hence, find whether the plane thus obtained contains the line x -1= 2y – 4 = 3z -12 .
Solution: The required plane is π : 2x – 3y + 4z –1+ λ(x – y + 4) = 0
⇒ :x(2 + λ) + y(–3– λ) + 4z –1+ 4λ = 0…(i)
As (i) is ⊥er to the plane r̅.(2ˆi – ˆj+ kˆ) + 8 = 0 so, 2(2 + λ) – (–3– λ) +1.4 = 0 ⇒ λ = –11/3
Replacing this value of λ in (i), we get : 5x – 2y –12z + 47 = 0…(ii)
In vector form, the plane is : r̅.(5ˆi – 2ˆj–12kˆ) + 47 = 0 .
Given line can be rewritten as x – 1/1 = y–2/1/2 = z– 4/1/3 . Therefore, point on the line is (1, 2, 4).
LHS of (ii) : 5x – 2y –12z + 47 = 5 x 1– 2 x 2 –12 x 4 + 47 = 0 = RHS.
Also, 5 x 1 – 2 x 1/2 – 12 x 1/3 = 0 [∵ a1 a2 + b1 b2 + c1 c2 = 0 here implies that the line is ⟂ to plane .
Hence the given line lies on the plane (ii).
OR
Find the vector and Cartesian equation of a line passing through (1, 2, –4) and perpendicular to the two lines x–8/3 = y+19/16 = z–10/7 and x–15/3 = y–29/8 = z–5/–5.
Solution: