Please refer to the Kinetic Theory Revision Notes given below. These revision notes have been designed as per the latest NCERT, CBSE and KVS books issued for the current academic year. Students will be able to understand the entire chapter in your class 11th Physics book. We have provided chapter wise Notes for Class 11 Physics as per the latest examination pattern.
Revision Notes Chapter 13 Kinetic Theory
Students of Class 11 Physics will be able to revise the entire chapter and also learn all important concepts based on the topic wise notes given below. Our best teachers for Grade 11 have prepared these to help you get better marks in upcoming examinations. These revision notes cover all important topics given in this chapter.
Boyle’s Law: At constant temperature volume of given mass of gas is inversely proportional to its pressure.

Charle’s Law: At constant pressure volume of a given mass of gas is directly proportional to its absolute temperature.

*For 1° rise in temp.
Vt = Vo (1 + t/273.15)
Gay Lussac’s Law: At constant volume, pressure of a given mass of gas is directly proportional to its absolute temp.
P/T = constant
For 10C rise in temperature Pt= Po (1 + t/273.15)
Ideal Gas Equation: for n mole of gas
PV=nRT,
for 1 mole , PV=RT
Universal gas constant: R = 8.31 J mol-1K-1
Boltzmann constant: kB = R/NA where kB = Boltzmann constant, NA = Avogadro’s no.
Ideal gas: A gas which obeys gas law strictly is an ideal or perfect gas. The molecules of such a gas are of point size and there is no force of attraction between them.
Assumptions of Kinetic Theory of Gases
1. All gases consist of molecules which are rigid, elastic spheres identical in all respect for a given gas.
2. The size of a molecule is negligible as compared with the average distance between two molecules.
3. During the random motion, the molecules collide with one another and with the wall of the vessel.The collisions are almost instantaneous.
4. The molecular density remains uniform throughout the gas.
5. The collisions are perfectly elastic in nature and there are no forces of attraction or repulsion between them.
Pressure exerted by gas:

Where: n=no. of molecules per unit volume.
m=mass of each molecule.
V¯2=mean of square speed.
V = Volume
M = mass of gas
Average Kinetic energy of a gas: If M is molecular mass and V is molecular volume and m is mass of each molecule. Then
1. Mean K.E per mole of a gas,

2. Mean K.E per molecule of a gas,
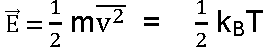
3. K.E of 1gram of gas,

Avogadro Law: Equal volume of all gases under similar condition of temp. and pressure contain equal number of molecules.
Avogadro Number:
NA =6.0225 x 1023 mol -1
Graham’s Law of diffusion :

r = rate of diffusion
P = density
Delton’s law of partial pressure: Total pressure exerted by a mixture of nonreacting gases occupying a given volume is equal to the sum of partial pressures which gas would exert if it alone occupied the same volume at given temp.
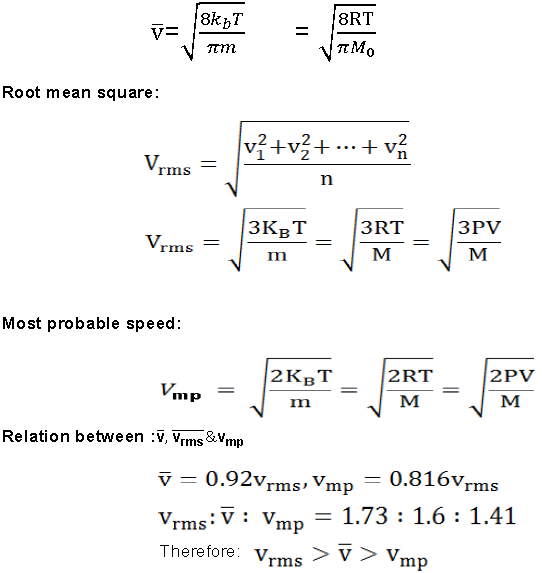
Degree of freedom:
f = 3N-k
where , f = no. of degree of freedom.
N = no. of of atoms in a molecule. k = no. of independent relation between the atoms.
1. Monoatomic gas – 2 degree of freedom.
2. Diatomic gas – 5 degree of freedom.
Law of equipartion of energy: For any thermodynamical system in thermal equilibrium, the energy of the system is equally divided amongst its various degree of freedom and energy associated with each degree of freedom corresponding to each molecule is 1/2 KBT, where KB is the Boltzmann’s constant and T is absolute temperature.
➤ The law of equipartition of energy holds good for all degrees of freedom whether translational , rotational or vibrational.
➤ A monoatomic gas molecule has only translational kinetic energy

So a monoatomic gas molecule has only three (translational) degrees of freedom.
➤ In addition to translational kinetic energy, a diatomic molecule has two rotational
Kinetic energies
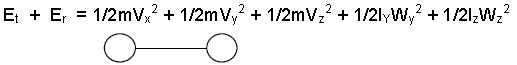
Here the line joining the two atoms has been taken as x-axis about which there is no rotation. So, the degree of freedom of a diatomic molecule is 5, it does not vibrate.
At very high temperature, vibration is also activated due to which two extra degree of freedom emerge from vibrational energy. Hence at very high temperature degree of freedom of diatomic molecule is seven.
(Each translational and rotational degree of freedom corresponds to one mole of
absorption of energy and has energy 1/2kBT) .
Internal Energies & specific heats of monoatomic, diatomic& polyatomic gases:
1. If ‘f’ is degree of freedom then for a gas of polyatomic molecules energy associated with 1 mole of gas,

2. For a monoatomic gas f=3,

3. For a diatomic gas with no vibrational mode f=5, so

4. For a diatomic gas with vibrational mode f=7, so

Meanfree path: It is the average distance covered by a molecule between two successive collisions. It is given by,

Where,n is no. density and ‘d’ is diameter of the molecule.
Brownian Equation :- The zig-zag motion of gas molecules is Brownian motion which occurs due to random collision of molecules.
Memory Map
Kinetic Theory of gases

