We have provided CBSE Class 10 Mathematics Sample Paper with solutions below. These Sample guess papers have been prepared as per the latest examination guidelines and paper pattern issued by CBSE. Students of Class 10 should practice all practice papers for Class 10 Mathematics given below as it will help them top improve their understanding of the subject. Please click on the links below to access free sample paper for Mathematics Class 10.
Sample Papers for Class 10 Mathematics
CBSE Class 10 Mathematics Term 2 Sample Paper Set A
SECTION – A
1. If the numbers 2n – 1, 3n + 2 and 6n – 1 are in A.P., then find n and hence find the numbers.
Answer : Let 2n – 1, 3n + 2 and 6n – 1 are in A.P.
∴ (3n + 2) – (2n – 1) = (6n – 1) – (3n + 2)
⇒ n + 3 = 3n – 3 ⇒ 6 = 2n ⇒ n = 3
∴ Numbers are : 2(3) –1 = 5, 3(3) +2 = 11 and 6(3) –1 = 17.
2. A solid iron rectangular block of dimensions 4.4 m, 2.6 m and 1 m is recast into a hollow cylinder of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
Answer : Volume of iron = (440 × 260 × 100) cm3
Internal radius of the pipe = 30 cm
External radius of the pipe = (30 + 5)cm = 35 cm
Let the length of the pipe be h cm.
Volume of iron in the pipe = (External volume) – (Internal volume)

OR
If the diameter of cross-section of a wire is decreased by 5%, how much percent will the length be increased so that volume remains the same?
Answer :
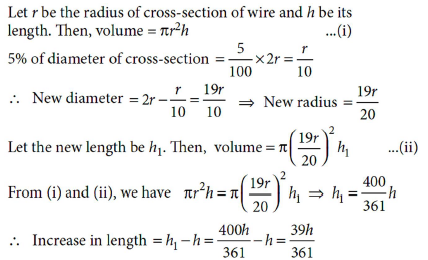
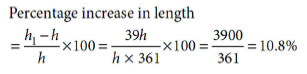
3. Find k so that the quadratic equation (k + 1)x2 − 2(k + 1)x + 1 = 0 has equal roots.
Answer : We have (k + 1)x2 – 2(k + 1)x + 1 = 0
Comparing with Ax2 + Bx + C = 0 we get A = (k + 1),B,= -2(k+ 1), C= 1
If roots are equal, then D = 0, i.e. B2 – 4AC = 0
⇒ B2 = 4AC
⇒ 4(k+ 1)2 = 4(k+ 1)
⇒ k2 + 2k + 1 = k + 1
⇒ k2 + k = 0
⇒ k(k + 1) = 0
⇒ k = 0, – 1
Since k = – 1 does not satisfy the equation, thus k = 0
OR
If one root of the quadratic equation 3x2 + px + 4 = 0is 2/3, then find the value of p and the other root of the equation.
Answer :
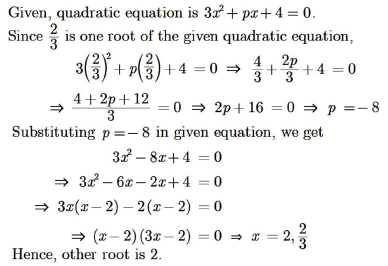
4. The difference of mother’s age and her daughter’s age is 21 years and the twelfth part of the product of their ages is less than the mother’s age by 18 years. Find their ages.
Answer :
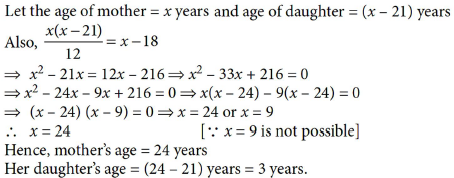
5. In figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120⁰, then prove that OR = PR + RQ.
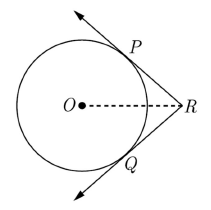
Answer :
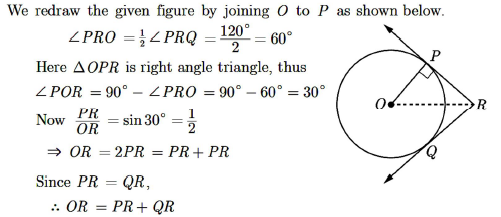
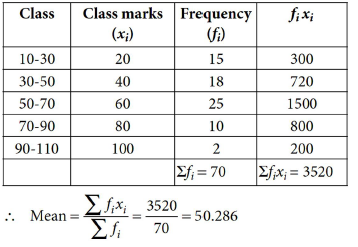
6. Calculate the mean for the following frequency distribution:

Answer :
SECTION – B
7. Draw a circle of radius 3.5 cm. Draw two tangents to the circle which are perpendicular to each other.
Answer : Steps of construction :
Step-I : Draw a circle of radius 3.5 cm with centre O.
Step-II : Draw a diameter AB.
Step-III : Construct ∠AOP = 90°.
Step-IV : At P and B, draw PY ⊥ OP and BX ⊥ OB.
Step-V : Let PY and BX intersect at D.
Hence, DB and DP are required tangents to the circle perpendicular to each other.

8. At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30°. The angle of depression of the reflection of the cloud in the lake, at A is 60°. Find the distance of the cloud from A.
Answer : Let DE be the level of water and cloud be at position B which is h m above the level of water and reflection of cloud be at F and AC = DE = x m.
∴ BC = (h – 20)m, CF = (h + 20) m
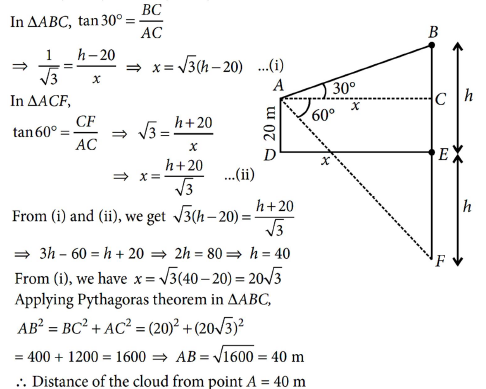
OR
The angles of depression of the top and bottom of a 12 m tall building, from the top of a multistoreyed building are 30° and 60° respectively. Find the height of the multi-storeyed building.
Answer : Let AB be the building and CD be the multi-storeyed building of height h m.
Here, AB = CE = 12 m and DE = (h – 12) m
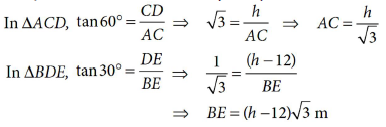
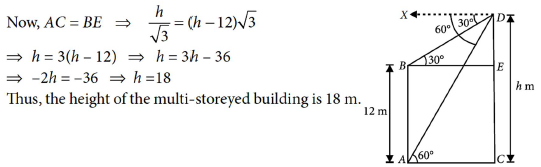
9. The following table gives the literacy rate of 40 cities :

Find the modal literacy rate.
Answer : From the given data, we observe that, highest frequency is 10, which lies in the class interval 50-60.
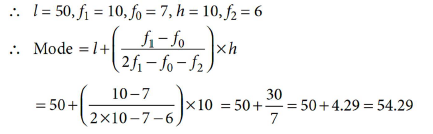
10. The median of the following data is 525. Find the values of x and y , if total frequency is 100 :
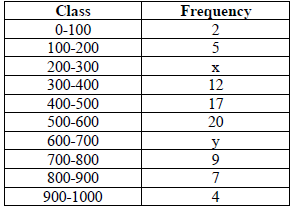
Answer :

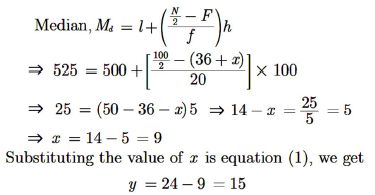
SECTION – C
11. A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weights, a conical hole is drilled in the cylinder. The conical hole has a radius of 3/2 cm and its depth 8/9 cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
Answer :

OR
A hollow cylindrical pipe is made up of copper. It is 21 dm long. The outer and inner diameters of the pipe are 10 cm and 6 cm respectively. Find the volume of copper used in making the pipe.
Answer : Volume of copper used in making the pipe is equal to the difference of volume of external cylinder and volume of internal cylinder.
Height of cylindrical pipe, h = 21 dm = 210 cm
External Radius, R = 10/2 = 5 cm
Internal Radius, r = 6/2 = 3 cm
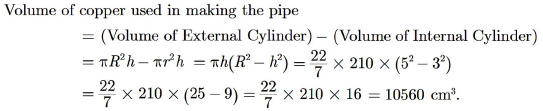
12. In the given fig., ΔABC is circumscribed touching the circle at P, Q, R if AP = 4 cm, BP = 6 cm, AC = 12 cm, then find radius of circle.
Answer : We have, AP = 4 cm, BP = 6 cm and AC = 12 cm
Since the length of tangents drawn from an external point to a circle, are equal.
∴ AP = AR ⇒ AR = 4 cm
Also, BP = BQ ⇒ BQ = 6 cm
and CR = CQ ⇒ CR = AC – AR = (12 – 4) cm = 8 cm
Now, BC = BQ + CQ = (6 + 8) cm = 14 cm

CASE STUDY QUESTION – 1
13. We can find A.P. in many situations in our day-to-day life. One such example is a tissue paper roll, in which the first term is the diameter of the core of the roll and twice the thickness of the paper is the common difference. If the sum of first n rolls of tissue on a roll is Sn = 0.1n2 +7.9n, then answer the following questions.

(i) Find Sn – 1.
(ii) What is the diameter of roll when one tissue sheet is rolled over it?
Answer :
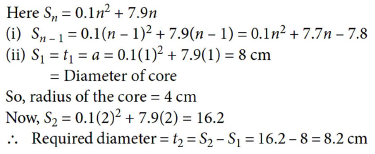
CASE STUDY QUESTION – 2
14. From his hotel room window on the fourth floor, Ranjan notices some window washers high above him on the hotel across the street.

Curious as to their height above ground, he quickly estimates the buildings are 60 m apart, the angle of elevation to the workers is about 600, and the angle of depression to the base of the hotel is about 300.
(i) How high above ground is the window of Ranjan’s hotel room?
(ii) How high above ground are the workers?
Answer :


