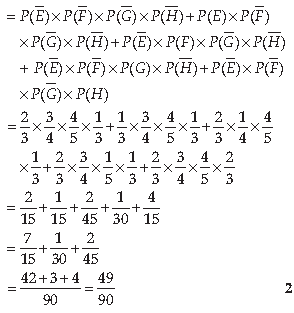See below CBSE Class 12 Mathematics Term 2 Sample Paper Set A with solutions. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern issued by CBSE for the current academic year. All sample papers provided by our Class 12 Mathematics teachers are with answers. You can see the sample paper given below and use them for more practice for Class 12 Mathematics examination.
CBSE Sample Paper for Class 12 Mathematics Term 2 Set A
Section – A

Answer.
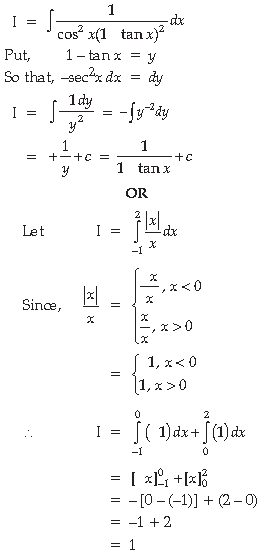
2. Show that the function y = ax + 2a2 is a solution of the differential equation
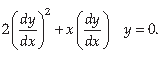
Answer.
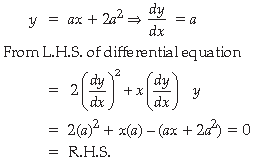
3. If â. b̂ and are mutually perpendicular unit vectors, then find value of |2â + b̂ + |.
Answer. â. b̂ and are mutually perpendicular unit vectors, i.e..,
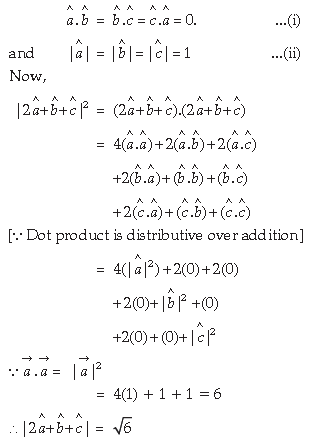
4. A line passes through the point with position vector 2î – 3ĵ + 4k̂ and makes angles 60°, 120°, and 45° with x, y and z-axis respectively. Find the equation of the line in the Cartesian form.
Answer.

5. Find the probability distribution of X, the number of heads in a simultaneous toss of two coins.
Answer. Let X be the number of heads.
Possible values of X are 0, 1, 2

6. The probability that it will rain on any particular day is 50%. Find the probability that it rains only on
first 4 days of the week.
Answer. P(rain on any particular day)
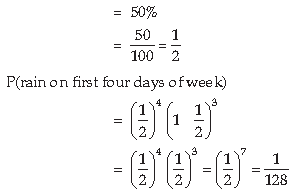
Section – B
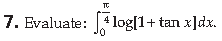
Answer.
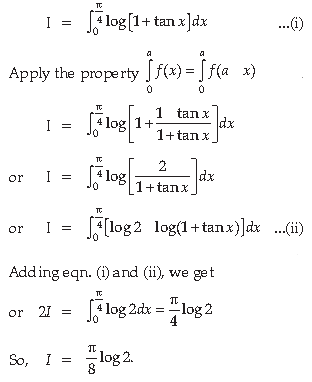
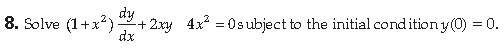
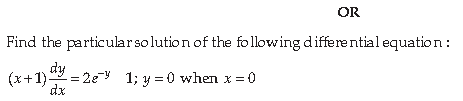
Answer. Given differential equation can be written as:

9. Find the area of the parallelogram whose diagonals are represented by the vectors a̅ = 2î – 3ĵ + 4k̂ and b̅ = 2î – ĵ + 2k̂
OR
Find λ and μ if (î + 3ĵ + 9k̂) x (3î – λĵ + μk̂) = 0¯
Answer. The vector equation for diagonals are a̅ = 2î – 3ĵ + 4k̂ and b̅ = 2î – ĵ + 2k̂


10. Find the value of l, so that the lines
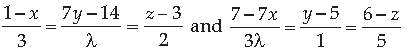
are at right angles. Also, find whether the lines are intersecting or not.
Answer. Given lines are :

Section – C
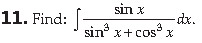
Answer. Let
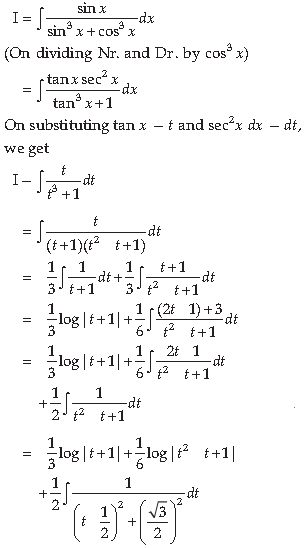
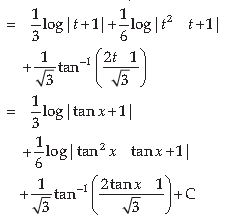
12. Find the area of the region bounded by the curve x2 = 4y and the straight-line x = 4y – 2
OR
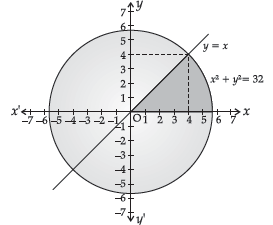
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32
Answer. As x2 = 4y and x = 4y – 2
So, x2 = x + 2
x2 x 2 = 0
(x – 2)(x +1) = 0
x = -1, 2
Graphs of parabola x2 = 4y and x = 4y − 2 are shown in the following figure:

We have y = 0, y = x and the circle x2 + y2 =32 in the first quadrant.
Solving y =x with the circle
x2 + x2 = 32
x2 = 16
x = 4 (In the first quadrant)
When x = 4, y = 4 for the point of intersection
of the circle with the x-axis.
Put y = 0 in circle
x2 + 0 = 32
x = ± 4√2
So, the circle intersects the x-axis at
( ± 4 √2, 0).

13. Find the shortest distance between the lines r̅ = 3î + 2ĵ + 2k̂ + λ(î + 2ĵ + 2k̂) and r̅ = 5î – 2ĵ + μ(3î + 3ĵ + 6k̂)
Answer. We have

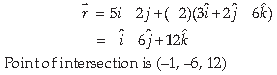
Case-Based/Data Based
14. Board exam are near by, so Mr. Sharma decided to check the preparation of the few weak students in the class. He chooses four students A, B, C and D then a problem in mathematics is given to those four students A, B, C, D. Their chances of solving the problem, respectively, are
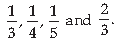
based on the given information answer the following questions. What is the probability that:
(i) the problem will be solved?
(ii) at most one of them solve the problem?

Answer. Let
E be the event = A solves the problem
F be the event = B solves the problem
G be the event = C solves the problem
H be the event = D solves the problem
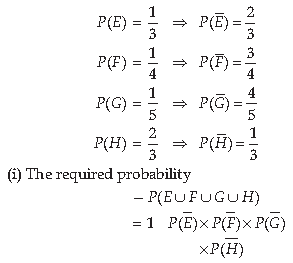
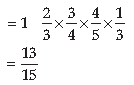
(ii) The required probability