See below CBSE Class 12 Mathematics Sample Paper Set H with solutions. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern issued by CBSE for the current academic year. All sample papers provided by our Class 12 Mathematics teachers are with answers. You can see the sample paper given below and use them for more practice for Class 12 Mathematics examination.
SECTION – A
1. Write the value of
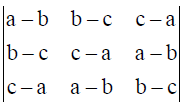
Solution:

2. If
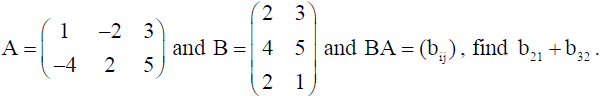
Solution:
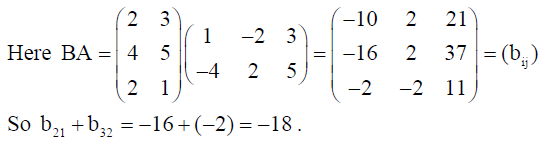
3. Write the number of all possible matrices of order 2 x 3 with each entry 1 or 2.
Solution: Any matrix of order 2×3 shall have 6 elements which are to filled by either 1 or 2 (i.e., in 2 ways). So, total number of all possible matrices are same as the number of ways of filling these entries 1 or 2 in 6 places. Hence total number of matrices are 2x 2x 2x 2x 2×2 = 26 or 64.
4. Write the coordinates of the point which is the reflection of the point (α,β, γ) in the XZ-plane.
Solution: Reflection of (α,β, γ) in XZ-plane is (α,-β, γ) .
5. Find the position vector of the point which divides the join of points with position vectors a̅ + 3b̅ and a̅ – b̅ internally in the ratio 1 : 3.
Solution: Required position vector is
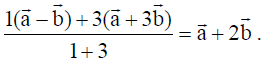
6. If |a̅| = 4 , |b̅| = 3 and a̅.b̅ = 6√3 , then find the value of |a̅ x b̅| .
Solution:
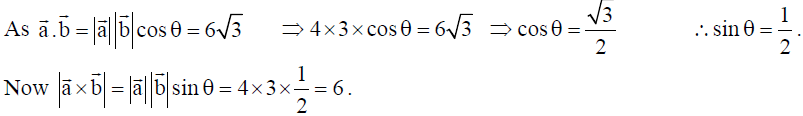
SECTION – B
7. Solve for x : tan-1(2-x/2+x) = 1/2 tan-1 x/2 , x > 0 .
Solution: Given that tan-1(2-x/2+x) = 1/2 tan-1 x/2 , x > 0

OR
Prove that : 2sin-1(3/5) – tan-1(17/31) = π/4 .
Solution:
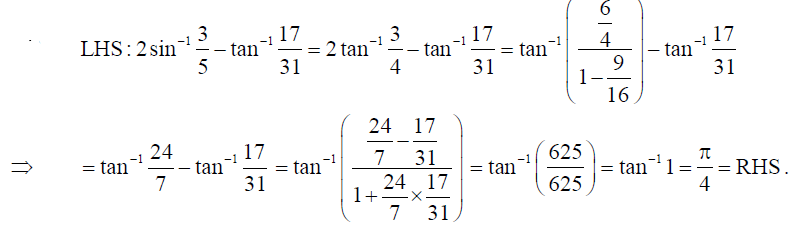
8. On her birthday Seema decided to donate some money to children of an orphanage home. If there were 8 children less, every one would have got ₹ 10 more. However, if there were 16 children more, every one would have got ₹ 10 less. Using matrix method, find the number of children and the amount distributed by Seema. What values are reflected by Seema’s decision?
Solution: Let the number of children be x and the amount distributed by Seema for one child be ₹ y.
So, (x – 8)(y +10) = xy ⇒ 5x – 4y = 40…(i)
and (x +16)(y -10) = xy ⇒ 5x – 8y = – 80…(ii)
To solve (i) and (ii), let 8
Clearly x = 32, y = 30.
Hence the number of children = 32 and the amount distributed by Seema = ₹ 30.
Value reflected : Helpfulness towards the needy people.
9. If x = ecos2t and y = esin 2t , prove that dy/dx = – y log x/x log x .
Solution: Here x = ecos2t and y = esin 2t ⇒ loge x = loge (e cos2t) and loge y = loge (esin2t)
⇒ loge x = cos 2t log (e) and loge y = sin 2t loge (e) [As loge (e) =1
∴ loge x = cos 2t and loge y = sin 2t
Squaring and then adding these two equations, (loge x)2 + (loge y)2 = cos2 2t + sin2 2t
⇒ (loge x)2 + (loge y)2 =1 ∴ d/dx [(loge x)2 + (loge y)2] = d/dx (1)
⇒ 2(loge x) x 1/x + 2(loge y) x 1/y x dy/dx = 0 ⇒ loge y/y x dy/dx = -loge x/x ∴ dy/dx = -y log x/x log y .
OR
Verify Mean value theorem for the function f (x) = 2sin x + sin 2x on [0, π] .
Solution We have f (x) = 2sin x + sin 2x which is
(i) continuous on [ 0,π] and, (ii) f ‘(x) = 2cos x + 2cos 2x so, f (x) is differentiable on ( 0,π).
Thus, f (x) satisfies both the conditions of MV Theorem. Consequently, there exists at least
one value of c ∈ (0,π) such that f'(c) = f(π) – f(0)/π – 0
As f (0) = 2sin 0+ sin 2(0) = 0 and f (π) = 2sin π + sin 2π = 0

10. Show that the function f given by f(x) =
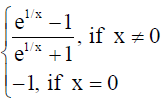
is discontinuous at x = 0 .
Solution:
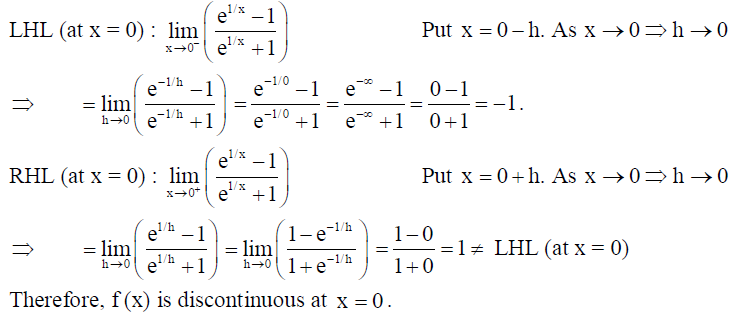
11. Find the equation of the tangent line to the curve y = √5x – 3 – 5 , which is parallel to the line 4x – 2y + 5 = 0 .
Solution:
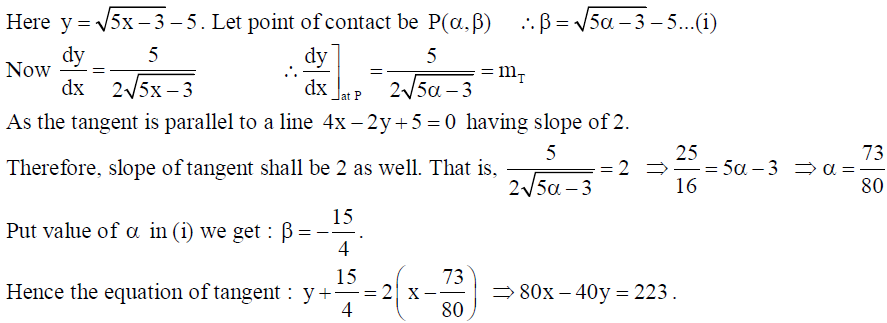
12. Evaluate :
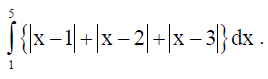
Solution:
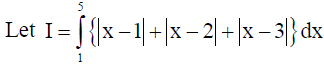
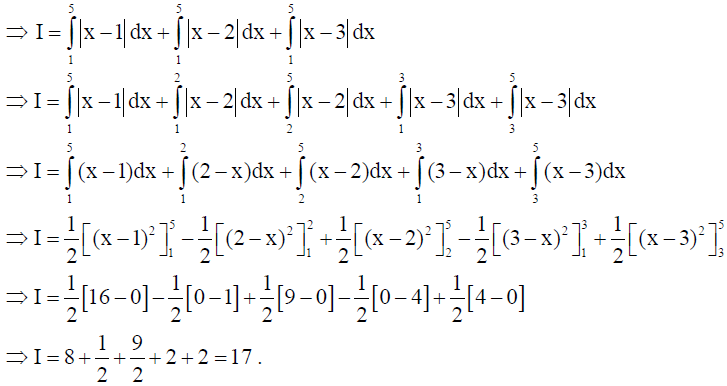
OR
Evaluate :

Solution

13. Find :
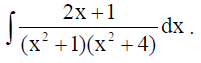
Solution:
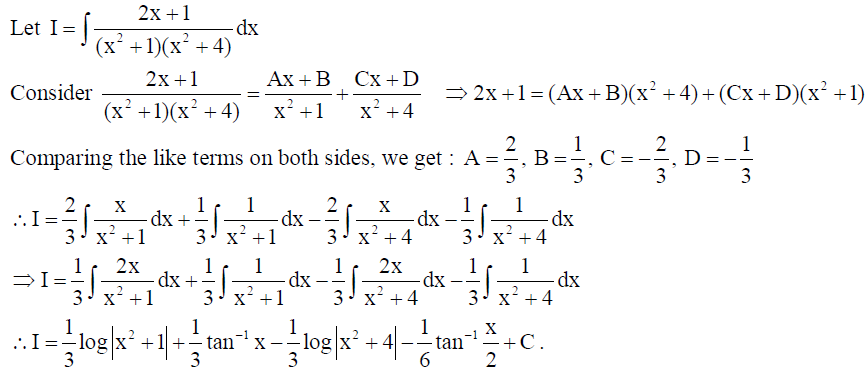
14. Find :

Solution:

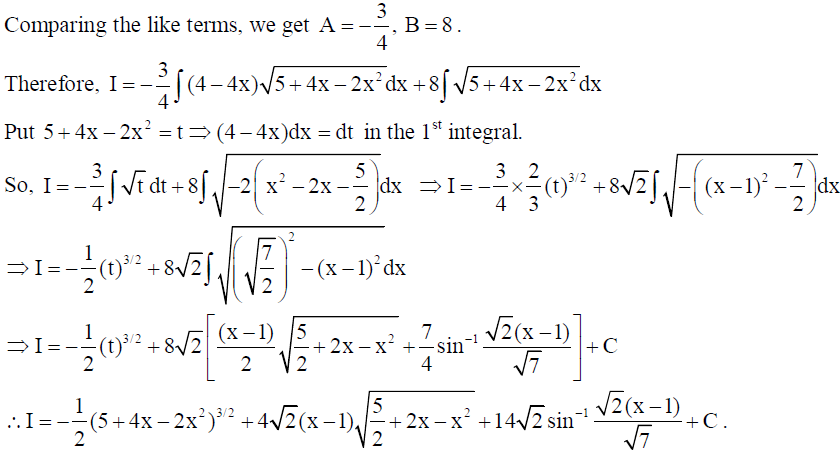
15. Solve the differential equation : x dy/dx + y – x + xy cot x = 0 ; x ≠ 0 .
Solution:
16. Solve the differential equation : (x2 + 3xy + y2 )dx – x2dy = 0 given that y = 0 when x =1.
Solution:
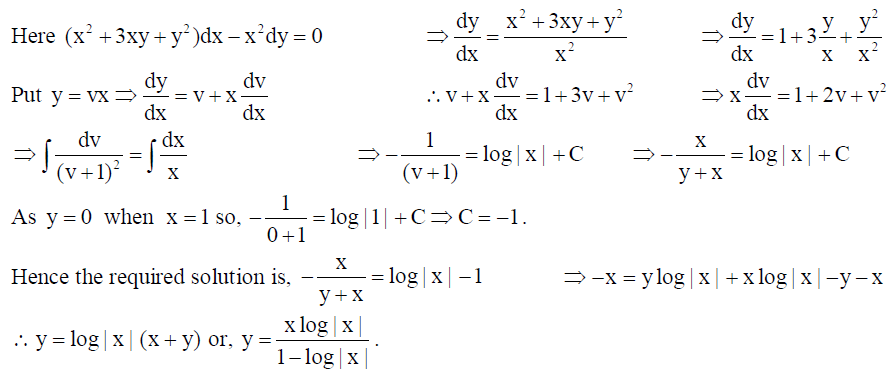
17. Find the angle between the vectors a̅ + b̅ and a̅ – b̅ if a̅ = 2î – ĵ – 2k̂, and hence find a vector perpendicular to both a̅ + b̅ and a̅ – b̅ .
Solution: Here a̅ + b̅ = 5î + k̂ and a̅ – b̅ = -î – 2ĵ + 5k̂.
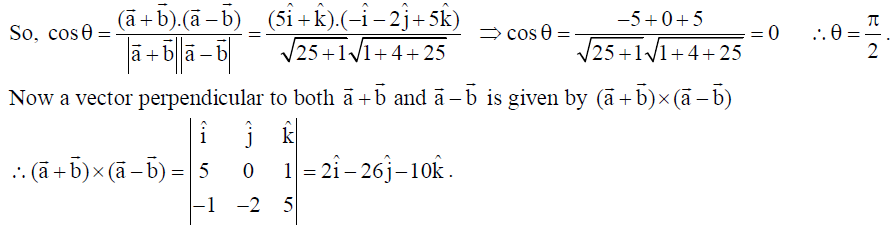
18. Show that the lines x-1/3 = y-1/-1 = z+1/0 and x-4/2 = y/0 = z+1/3 intersect. Find their point of intersection.
Solution: Let L1 : x-1/3 = y-1/-1 = z+1/0 and L2 : x-4/2 = y/0 = z+1/3 = μ
∴ Coordinates of random points on the given lines are P(3λ +1,-λ +1,-1) & Q(2μ + 4,0,3μ -1)
If the lines intersect, then they have a common point for some value of λ and μ .
3λ – 2μ = 3…(i), – λ + 1= 0…(ii), 3μ -1= -1…(iii)
Solving (ii) and (iii) we get : λ = 1 and μ = 0
As LHS of (i) : 3λ – 2μ = 3X1- 2X0 = 3 = RHS of (i)
Since λ =1 and μ = 0 satisfy the equation (i) therefore, the given lines intersect.
The point of intersection is P or Q (4, 0, –1).
19. A committee of 4 students is selected at random from a group consisting of 7 boys and 4 girls.
Find the probability that there are exactly 2 boys in the committee, given that at least one girl must be there in the committee.
Solution: Let A : exactly 2 boys are in the committee, B : at least one girl must be in the committee.
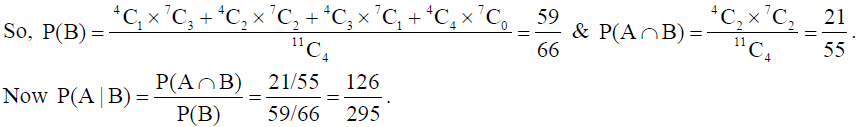
OR
A random variable X has the following probability distribution :

Find the value of C and also calculate the mean of this distribution.
Solution:
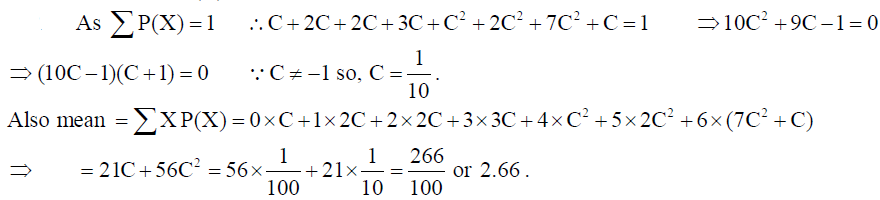
SECTION – C
20. Show that the relation R defined by (a, b)R(c,d)⇒ a + d = b + c on the A x A , where A = {1, 2,3,…,10} is an equivalence relation. Hence write the equivalence class [(3, 4)]; a, b, c,d ∈ A .
Solution: Here (a, b)R(c,d)⇒ a + d = b + c on AxA , where A={1, 2,3,…,10}.
Reflexivity : Let (a, b) be an arbitrary element of A x A. Then, (a, b)∈ A x A ∀ a, b ∈ A.
So, a + b = b + a ⇒ (a, b) R (a, b).
Thus, (a, b) R (a, b) ∀ (a, b)∈ A x A. Hence R is reflexive.
Symmetry : Let (a, b), (c, d)∈ A x A be such that (a, b) R (c, d).
Then, a + d = b + c ⇒ c + b = d + a ⇒ (c, d) R (a, b).
Thus, (a, b) R (c, d) ⇒ (c, d) R (a, b) ∀ (a, b), (c, d)∈ A x A. Hence R is symmetric.
Transitivity : Let (a, b), (c, d), (e, f)∈ A x A be such that (a, b) R (c, d) and (c, d) R (e, f).
Then, a + d = b + c and c + f = d + e ⇒ (a + d) + (c + f) = (b + c) + (d + e) ⇒ a + f = b + e
⇒ (a, b) R (e, f). That is, (a, b) R (c, d) and (c, d) R (e, f) ⇒ (a, b) R (e, f) ∀ (a, b), (c, d), (e, f)∈ A x A. Hence R is transitive.
Since R is reflexive, symmetric and transitive so, R is an equivalence relation as well.
For the equivalence class of [(3, 4)], we need to find (a, b) s. t. (a, b) R (3, 4) ⇒ a + 4 = b + 3
⇒ b – a = 1.
So, [(3, 4)] = {(1,2), (2,3), (3,4), (4,5), (5,6), (6,7), (7,8), (8,9), (9,10)}.
21. Solve for x :
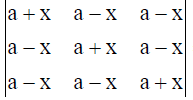
= 0 , using properties of determinants.
Solution:
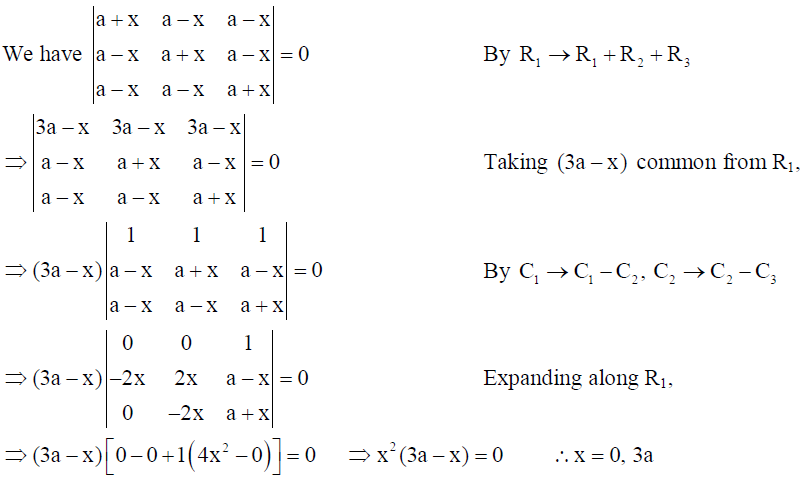
OR
Using elementary row operations, find the inverse of the matrix A =
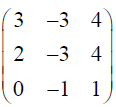
and hence solve the following system of equations : 3x – 3y + 4z = 21, 2x – 3y + 4z = 20, -y + z = 5 .
Solution:


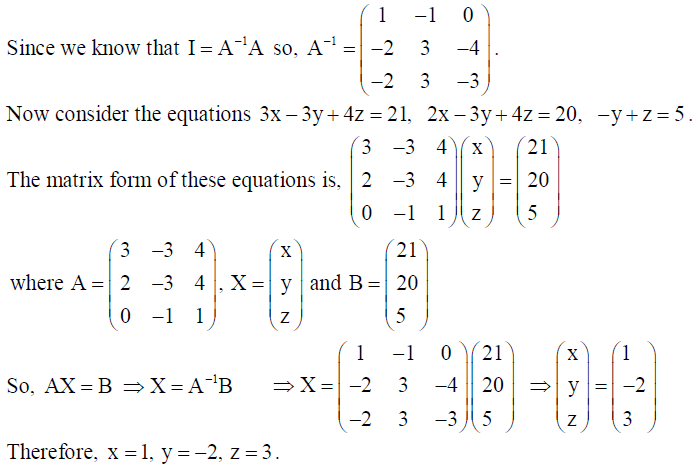
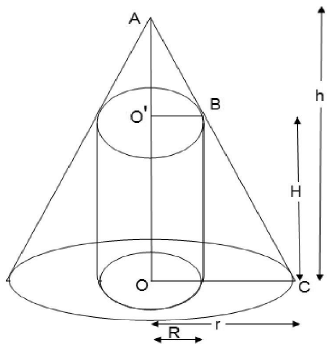
22. Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle α is one-third that of the cone and the greatest volume of the cylinder is 4/27 πh3 tan2 α .
Solution: Let height and radius of the cylinder inscribed in the cone be H and R respectively.
Let ∠AOC = α. Since ΔAOC~ ΔAO’B


OR
Find the intervals in which the function f (x) = 4 sin x/2+ cos x – x – 0 ≤ x ≤ 2π is strictly increasing or strictly decreasing.
Solution:

23. Using integration find the area of the triangle formed by negative x-axis and tangent and normal to the circle x2 + y2 = 9 at (-1, 2 √2) .
Solution: The equation of circle is x2 + y2 = 9
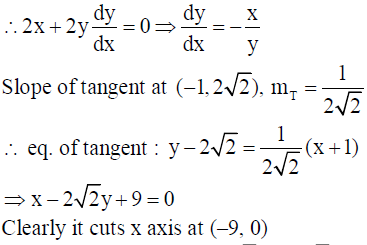


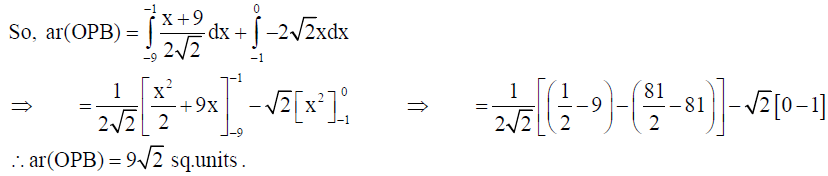
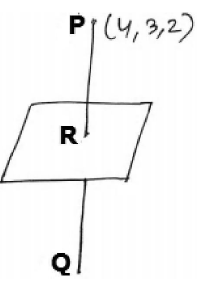
24. Find the coordinates of the foot of perpendicular and perpendicular distance from the point P(4, 3, 2) to the plane x + 2y + 3z = 2 . Also find the image of P in the plane.
Solution: Let π : x + 2y + 3z = 2 . The d.r.’s of its normal are 1, 2, 3.
Draw PR ⊥ plane π .

25. A, B and C throw a pair of dice in that order alternatively till one of them gets a total of 9 and wins the game. Find their respective probabilities of winning, if A starts first.
Solution: Let E : getting a total of 9 ∴ E = {(3,6),(4,5),(5, 4),(6,3)}

And, finally P(C wins) 1 = [P(A wins) + P(B wins)] = 1-[81/217 + 72/217] = 64/217 .
26. A company manufactures two types of cardigans : type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72, 000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the
company. Solve it graphically and find the maximum profit.
Solution: Let number of cardigans of type A and type B be x and y respectively.
To maximize : Z = 100x = 50y in ₹
Subject to constraints : x ≥ 0, y ≥ 0 ,
x + y ≤ 300,
360x + 120y ≤ 72000 ⇒ 3x + y ≤ 600,
y ≤ x + 200 ⇒ y – x ≤ 200

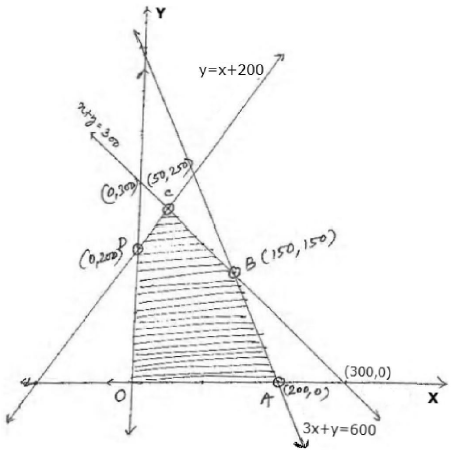
Hence no. of cardigans of type A = 150
and no. of cardigans of type B = 150.
Also maximum profit is ₹ 22500.


