Assignments for Class 10 Mathematics Triangles have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Triangles from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Triangles. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Triangles book and get good marks in class 10 exams.
Question. In the given figure, AB || CD then the value of ‘x’ is equal to
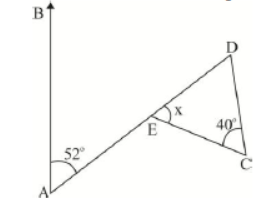
(A) 440
(B) 880
(C) 800
(D)1000
Answer
B
In the adjoining figure ABC is a triangle; P is an interior point in it. Three lines are drawn through the point P, parallel to three sides as shown in figure. The triangle is divided into six parts. The areas as 3 smaller triangles are 4, 9 and 16 units, then the area of triangle ABC is…….
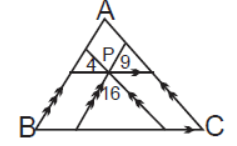
(A) 64
(B) 81
(C) 42
(D) 65
Answer
B
Question. If ∠BAE = ∠ECD then ΔABD and ΔCDEwill be
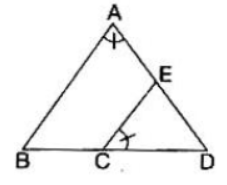
(A) congruent
(B) similar
(C) right angle triangle
(D) cannot say
Answer
B
Question. If ΔAEB and ΔDCAboth are right angled triangle then which of the following is correct?
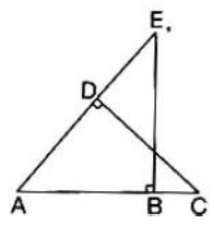
(A) CD/EB DA/AC
(B) AB/AC = AD/DC
(C) EA/AC = EB/CD
(D) none of these
Answer
C
ΔABC is an equilateral triangle, we have BD = EG = DF = DE = EC, then the ratio of the area of the portion to area of ΔABC is:
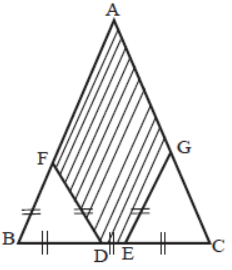
(A) 4/11
(B) 7/9
(C) 5/12
(D) 6/7
Answer
B
Question. In the given figure, AB divides ∠DACin the ratio 1 : 3 and AB = DB. Find the value of x.
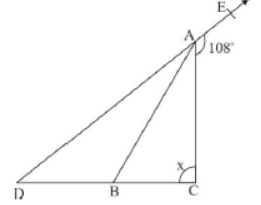
(A) 900
(B) 800
(C) 700
(D) 850
Answer
A
Question. In the quadrilateral ABCD 90 , ∠A = ∠C= 900 ,AE = 5cmand BE = 12cm and AC = 21 cm. If DF = x, then the value of x is:

(A) 6 (2/3) cm
(B) 10/7 cm
(C) 11 cm
(D) 13 cm
Answer
A
Question. In the given figure, o ∠A =1000 and AB = AC, find ∠B and ∠C.

(A) 400 ,400
(B) 600 ,200
(C) 450 ,350
(D) 250 ,550
Answer
A
Question. In the diagram ABCD is a rectangle with AE = EF =FB, the ratio of the areas of triangle CEF and that of rectangle ABCD is
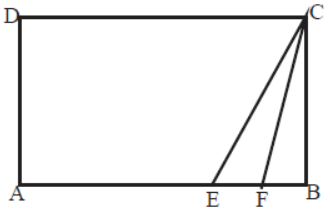
(A) 1 : 6
(B) 1 : 8
(C) 1 : 9
(D) 1 : 10
Answer
A
Question. Which of the following is not a criterion the congruence of triangles?
(A) SAS
(B) SSA
(C) ASA
(D) SSS
Answer
B
Question. In the given figure, The measure of ∠B’A’C’ is
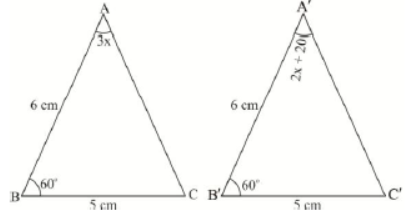
(A) 500
(B) 600
(C) 700
(D) 800
Answer
B
Question. In the figure, the area of square ABCD is 4 cm2 and E is midpoint of AB; F, G, H and K are the mid points of DE, CF, DG and CH respectively. The area of triangle KDC is

(A) 1/4 cm2
(B) 1/8 cm2
(C) 1/16 cm2
(D) 1/32 cm2
Answer
B
Question. In the given figure ABCD is a rectangle and all measurement is in centimeters. Find the area of the shaded region

(A) 240 cm2
(B) 205 cm2
(C) 105 cm2
(D) 95 cm2
Answer
C
Question. If A, B and C are mid-points of DE, EF and ED of ΔDEF then find the ratio of area of ΔABC and ΔDEF .
(A) 1 : 4
(B) 4 : 1
(C) 3 : 2
(D) 2 : 3
Answer
B
Question. Which of the following is correct?

(A) AC = AB
(B) AC = BC
(C) DC = BD
(D) BC = AC
Answer
C
Question. In the given figure, X is point in the interior of square ABCD.
AXYZ is also a square. If DY = 3cm, AZ = 2cm then length of BY is:
(A) 5 cm
(B) 6 cm
(C) 7 cm
(D) 8 cm
Answer
C
Question. In a square PQRS, A and B are two points on Ps and sR such that PA = 2As and RB = 2Bs. If PQ = 6, the area of the triangle ABQ is.
(A) 5sq. units
(B) 10sq. units
(C) 15sq. units
(D) None of these
Answer
B
Question. If ΔPQR ≅ ΔEFD, then ED = ?
(A) PQ
(B) QR
(C) PR
(D) none of these
Answer
C
Question. In the given figure, AB = AC, AD is the median to base BC. Then, ∠BAD= ?
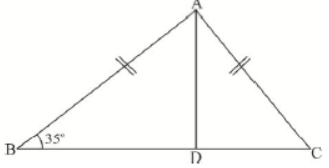
(A) 550
(B) 700
(C) 350
(D) 1100
Answer
A
The ratio of the area of A to that of C is 16 : 27 and the ratio of B to the area of C is 1 : 3. Find the ratio of the area of A to that of
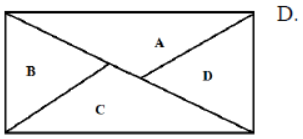
(A) 4 : 5
(B) 5 : 4
(C) 1 : 1
(D) None of these
Answer
A
Question. In ΔABC, o ∠B=∠C = 45 . Which is the longest side?
(A) AC
(B) AB
(C) BC
(D) none of these
Answer
C
Question. In ΔABC, if o ∠A = 500 and ∠B = 600 , determine the shortest and largest sides of the triangle.
(A) BC, AB
(B) AB, BC
(C) AC, BC
(D) none of these
Answer
A
Question. The fig. below has been obtained by folding a rectangle. The total area of the figure is 144 cm2. Had the rectangle not been folded, the current overlapping part would have been a square. What would have been the total area of the original unfolded rectangle?
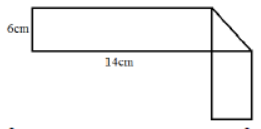
(A) 162m2
(B) 140cm2
(C) 142mm2
(D) 162cm2
Answer
D
Question. ABCD is a parallelogram, if the two diagonals are equal, find the measure of ΔABC.
(A) 50
(B) 60
(C) 90
(D) 100
Answer
C
Question. In the given figure, AC is the bisector of ∠BAD. Then CD = ?

(A) 2cm
(B) 3 cm
(C) 4 cm
(D) 5cm
Answer
C
Question. In ΔABCand ΔDEF such that ΔABC ≅ ΔFDE, and AB = 5 cm, ∠B = 400 , ∠A = 800 . Which of the following is true?
(A) DF = 5 cm, ∠F = 600
(B) DE = 5 cm, ∠E = 600
(C) DF = 5 cm, ∠E = 600
(D) DE = 5 cm,∠D = 400
Answer
C
Question. If XYZ is a triangle where ∠Z = 900 . If L is the mid-point of YZ then
(A) XY2 + 4XL2 = 3XZ2
(B) XY2 + 3XZ2 = 4XL2
(C) XY2 + XZ2 = XL2
(D) none of these
Answer
B
Question. If hypotenuse LM is common for both the triangles i.e., ΔKLMand ΔLMN then
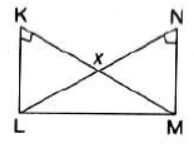
(A) KX x XM = LX x LM
(B) KX x KL = LM x MX
(C) KX x XM = LX x XN
(D) none of these
Answer
C
Question. In the triangles ABC and PQR, three equality relations between some parts are as follows:
AB = PQ, ∠B= ∠P , BC = PR Congruence conditions apply:
(A) SAS
(B) ASA
(C) SSS
(D)RHS
Answer
A
Question. In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of the vertex angle of the triangle is
(A) 1000
(B) 1200
(C) 1100
(D) 1300
Answer
A
VERY SHORT ANSWER TYPE QUESTIONS
Question. If the ratio of the corresponding medians of two similar triangles is 7 : 5, then what is the ratio of their corresponding sides?
Answer
7 : 5
Question. The lengths of sides of a triangle are 12 cm, 16 cm and 21 cm. The bisector of the greatest angle divides the opposite side into two parts. Find the length of these two parts.
Answer
9 cm, 12 cm
Question. In figure, find AD.
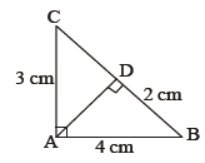
Answer
1.5 cm
Question. Is the triangle with sides 9 cm, 41 cm, 40 cm a right angled triangle?
Answer
yes
Question. If ΔABC ~ ΔPQR such that ar (ΔABC) = 81 cm2 and ar (ΔPQR) = 121 cm2. If QR = 22 cm, find BC.
Answer
18 cm
Question. In figure, ΔXMN ~ ΔXYZ, what is the measure of ΔXZY?
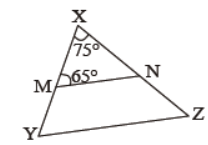
Answer
40°
Question. In figure, ∠ADB = ∠BAC = 90°. What is the value of x?

Answer
24 cm
Question. The perimeters of two similar triangles ABC and PQR are respectively 30 cm and 24 cm. If PQ = 8 cm, find AB.
Answer
10 cm
Question. In figure, express x in the terms of a, b and c.
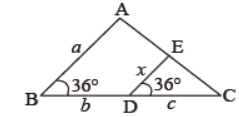
Answer
ac/b + c
Question. If ΔABC ~ ΔPQR and their corresponding altitudes are in the ratio 7 : 8, then what is the ratio of the area of ΔPQR to that of area of ΔABC?
Answer
64 : 49
Question. In figure, find x.
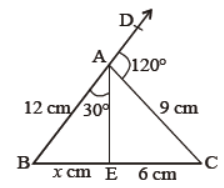
Answer
8 cm
Question. In figure, DE || BC. If AD/DB = 4/3 , then what is the value of AE/AC ?

Answer
4/7
Question. Two poles of height 6 m and 11 m are standing 12 m apart. What is the distance between their tops?
Answer
13 m
Question. If ΔABC ~ ΔXYZ and the ratio of area of ΔABC to that of area of ΔXYZ is 25 : 49, then what is the ratio of their corresponding medians?
Answer
5 : 7
Question. In figure, ΔABC and ΔDEC are the right triangles with ∠B = ∠E = 90°, find BE.
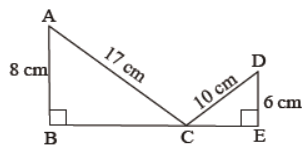
Answer
23 cm
Question. If the ratio of the corresponding sides of two similar triangles is 3 : 5, then what is the ratio of their corresponding heights?
Answer
3 : 5
Question. The area of the two similar triangles are in the ratio 81 : 121. What is the ratio of their corresponding sides?
Answer
9 : 11
Question. In figure, DE || BC, what is the value of x?
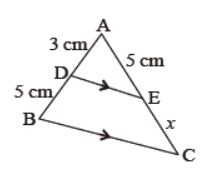
Answer
25/3 cm
Question. If ΔABC ~ ΔDEF such that BC = 5 cm, EF = 3 cm and ar (ΔDEF) = 36 cm2, find the area of ΔABC.
Answer
100 cm2
Triangles
Similar figures : Two polygons of the same number of sides are similar, if :
i) Their corresponding angles are equal.
ii) Their corresponding sides are in the same ratio (or proportion)
Properties for similar triangles
Area of similar triangles
A number of techniques can be applies in accordance with the similarity theorems to easily compute areas of similar triangles.
“The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides”
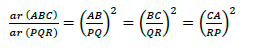
Properties of right angle triangle F
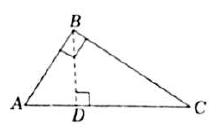
i) Pythagoras theorem AC2=AB2+BC2
ii) If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, then the triangles on both sides of the perpendicular are similar to the whole triangle and also to each other.
Two triangles are similar, if :
i) Their corresponding angle are equal ( AAA-criteria).
ii) Their corresponding sides are in the same ratio (SSS-criteri ).
iii) If one angle of a triangle is equal to the one angle of other triangle and sides including these angles angle are in proportion (SAS-criteri ).
Theorems used to prove similarity of triangles are :
I. Basic Proportionality Theorem (B.P.T.) (Theorem)
In a triangle, a line drawn parallel to one side, to intersect the other sides in distinct points, divides the sides in Δ the same ratio.
In ABC,if DE ∥ BC then F
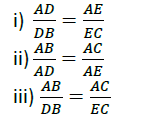
II. Converse of Basic proportionality Theorem
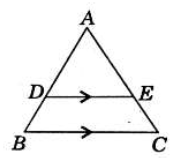
If a line divides any two sides of a triangle in the same ratio, the line is parallel to the third side. In Δ PA/SA =PT/TR, then AT ∥ QR.F
Solved Problems on Class 10 Triangles
Question. In Fig.4.18, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ^ BC and EF ^ AC, prove that ΔABD ~ΔECF.

Sol. We have, ∠B = ∠C [∴ ABC is an isosceles triangle with AB = AC]
Now, in ΔABD and ΔECF
∠ABD = ∠ECF [∴ ∠B = ∠C]
∠ADB = ∠EFC = 90° [∴ AD ^ BC and EF ^ AC]
∴ ΔABD ~ ΔECF (By AA criterion of similarity)
Question. In Fig. 4.12, AO/OC=BO/OD = 1/2 and AB = 5 cm. Find the value of DC.
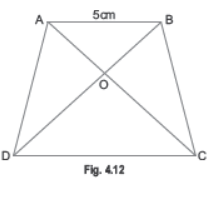
Sol. In ΔAOB and ΔCOD, we have
∠AOB = ∠COD [Vertically opposite angles]
AO/OC=BO/OD [Given]
So, by SAS criterion of similarity, we have ΔAOB ~ΔCOD
⇒ AO/OC=BO/OD=AB/DC
⇒ 1/2= 5/DC [Q AB = 5 cm]
⇒ DC =10 cm
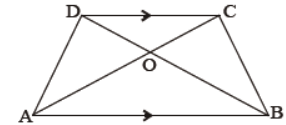
Question. Diagonals AC and BD of a trapezium ABCD with AB||DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OA/OC=OB/OD.
Sol. Given: ABCD is a trapezium in which AB||DC.
To prove: OA/OC=OB/OD
Proof: In DOAB and DODC, we have
∠OAB = ∠OCD (Alternate angles)
∠AOB = ∠DOC (Vertically opposite angles)
∠ABO = ∠ODC (Alternate angles)
∴ ΔOAB ~ΔOCD (By AA criterion of similarity)
Hence, OA/OC=OB/OD
Question. ABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that
AO/BO=CO/DO.
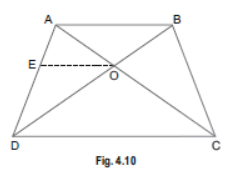
Sol. Given: ABCD is a trapezium, in which AB||DC and its diagonals intersect each other at the point O.
To prove: AO/BO=CO/DO
Construction: Through O, draw OE|| AB i.e., OE||DC.
Proof: In ΔADC, we have OE||DC (Construction)
∴ By Basic Proportionality Theorem, we have
AE/ED=AO/CO …(i)
Now, in DABD, we have OE|| AB (Construction)
∴ By Basic Proportionality Theorem, we have
ED/AE=DO/BO ⇒ AE/ED=BO/DO …(ii)
From (i) and (ii), we have
AO/CO=BO/DO ⇒ AO/BO=CO/DO
Question. S and T are points on sides PR and QR of DPQR such that ∠P = ∠RTS. Show that ∠RPQ ~DRTS.
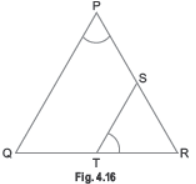
Sol. In DRPQ and DRTS, we have
∠RPQ = ∠RTS (Given)
∠PRQ = ∠TRS = ∠R (Common)
∴ ΔRPQ ~ΔRTS (By AA criterion of similarity.)
Question. State which pairs of triangles in the following figures are similar. Write the similarity criterion used by you
for answering the question and also write the pairs of similar triangles in the symbolic form.

Sol. (i) In ΔABC and ΔPQR, we have
AB/QR= 2/4=1/2
AC/PQ= 3/6=1/2
BC/PR= 2.5/5=25/50=1/2
Hence, AB/QR=AC/PQ=BC/PR
∴ ΔABC ~ΔQRP by SSS criterion of similarity.
(ii) In ΔLMP and ΔDEF, we have
LP/DF=3/6=1/2, MP/DE=2/4=1/2, LM/EF=2.7/5.
Hence, LP/DF=MP/DE≠LM/EF
∴ ΔLMP is not similar to ΔDEF.
(iii) In ΔNML and ΔPQR, we have
∠M = ∠Q = 70°
Now, MN/PQ= 2.5/6=5/12.
And ML/QR= 5/10=1/2
Hence MN/PQ≠ML/QR
∴ ΔNML is not similar to ΔPQR because they do not satisfy SAS criterion of similarity.
Question. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
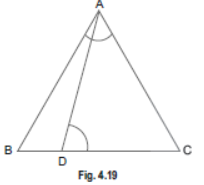
Sol. In ΔABC and ΔDAC, we have
ÐBAC = ∠ADC (Given)
and ∠C = ∠C (Common)
∴ ΔABC ~ ΔDAC (By AA criterion of similarity)
⇒ AB/DA=BC/AC=AC/DC
⇒ CB/CA=CA/CD
⇒ CA2 = CB ≠ CD
Question. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ~ΔCFB.

Sol. In ΔABE and ΔCFB, we have
∠AEB = ∠CBF (Alternate angles)
∠A = ∠C (Opposite angles of a parallelogram)
∴ ΔABE ~ΔCFB (By AA criterion of similarity)
Question. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Sol. Let AB be a vertical pole of length 6m and BC be its shadow and DE be tower and EF be its shadow. Join AC and DF.
Now, in ΔABC and ΔDEF, we have
∠B = ∠E = 90°
∠C = ∠F (Angle of elevation of the Sun)
∴ ΔABC ~ΔDEF (By AA criterion of similarity)
Thus, AB/DE=BC/EF
⇒ 6/h= 4/28 (Let DE = h)
⇒ 6/h=1/7
⇒ h = 42
Hence, height of tower, DE = 42 m
Question. Is the triangle with sides 12 cm, 16 cm and 18 cm a right triangle? Give reason.
Sol. Here, 122 + 162 = 144 + 256 = 400 ¹ 182
∴ The given triangle is not a right triangle.
3. Prove that the area of an equilateral triangle described on a side of a right-angled isosceles triangle is half the area of the equilateral triangle described on its hypotenuse.

Sol.Given: A ΔABC in which ÐABC = 90° and AB = BC. ΔABD and ΔACE are equilateral triangles.
To Prove: ar(ΔABD) = 1/2 × ar(ΔCAE)
Proof: Let AB = BC = x units.
∴ hyp. CA = √x2+x2 = x√2 units.
Each of the ΔABD and ΔCAE being equilateral, each angle of each one of them is 60°.
∴ ΔABD ~ ΔCAE
But, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
∴ ar( ABD)/ar (CAE)=AB2/CA2 = x2/(x√2)2 = x2/2x2=1/2
Hence, ar (ΔABD) = 1/2 × ar (ΔCAE)
Question. Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Sol. Since the perimeters and two sides are proportional
∴ the third side is proportional to the third side.
i.e., the two triangles will be similar by SSS criterion.
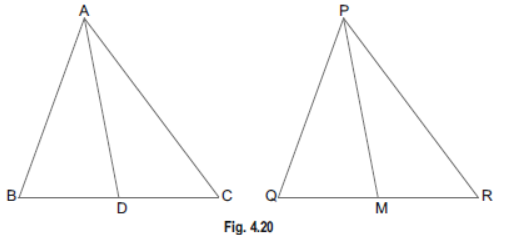
Question. In Fig. 4.17, ABC and AMP are two right triangles right-angled at B and M respectively. Prove that:
(i) ΔABC~ΔAMP (ii) CA/PA=BC/MP

Sol. (i) In DABC and DAMP, we have
∠ABC =∠AMP = 90° (Given)
And, ∠BAC = ∠MAP (Common angle)
∴ ΔABC ~ΔAMP (By AA criterion of similarity)
(ii) As DABC ~DAMP (Proved above)
∴ CA/PA=BC/MP (Sides of similar triangles are proportional)
Question. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
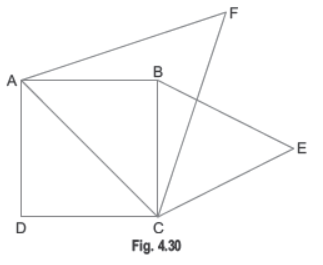
Sol. Let ABCD be a square and ΔBCE and ΔACF have been drawn on side BC and the diagonal AC respectively.
To prove: area (ΔBCE) = 1/2 area (ΔACF)
Proof: Since DBCE and DACF are equilateral triangles
ΔBCE ~ΔACF (by AAA criterion of similarity)
⇒ area(ΔBCE)/area(ΔACF)=BC2/AC2
⇒ area(ΔBCE)/area(ΔACF) =BC2/BC2 [Q Diagonal = 2 side, AC = 2BC]
⇒ area(ΔBCE)/area(ΔACF) = 1/2
⇒ area (ΔBCE) = 1 area (ΔACF)
Question. In Fig. 4.21, ABCD is a trapezium with AB||DC. If ΔAED is similar to DBEC, prove that AD = BC.
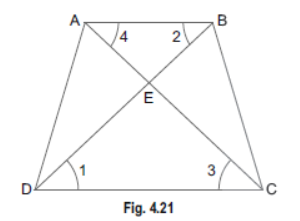
Sol. In ΔEDC and ΔEBA, we have
∠1 = ∠2 [Alternate angles]
∠3 = ∠4 [Alternate angles]
and ∠CED = ∠AEB [Vertically opposite angles]
∴ ΔEDC ~ΔEBA [By AA criterion of similarity]
⇒ ED/EB=EC/EA
⇒ ED/EC=EB/EA …(i)
It is given that ΔAED ~ΔBEC
∴ ED/EC=EA/EB=AD/BC …(ii)
From (i) and (ii), we get
EB/EA=EA/EB ⇒ (EB)2 = (EA)2 ⇒ EB = EA
Substituting EB = EA in (ii), we get
EA/EA=AD/BC
⇒ AD/BC ⇒ AD = BC
Question. If the areas of two similar triangles are equal, prove that they are congruent.

Sol. Given: Two triangles ABC and DEF, such that
DABC ~ΔDEF and area (ΔABC) = area (ΔDEF)
To prove: ΔABC ∼ ΔDEF
Proof: ΔABC ~ΔDEF
⇒ ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
and AB/DE=BC/EF=AC/DF
Now, ar (ΔABC) = ar (ΔDEF) (Given)
∴ ar(ABC )/ar(DEF )=1 …(i)
and AB/DE=BC/EF=AC/DF ar(ABC )/ar(DEF ) (∴ ΔABC ~ΔDEF) …(ii)
From (i) and (ii), we have
AB/DE=BC/EF=AC/DF
⇒ AB/DE=BC/EF=AC/DF
⇒ AB = DE, BC = EF, AC = DF
Hence, ΔABC ∼ ΔDEF (By SSS criterion of congruency)
Question. Let ΔABC~ΔDEF and their areas be respectively 64 cm2 and 121 cm2. If EF =15× 4 cm, find BC.

Sol. We have,
area of ABC/ area of DEF =BC2/EF2 (as ΔABC ~ΔDEF)
⇒ 64/=121 = BC2/EF2
⇒ 64/121=BC2/(15-4)
⇒ BC/15.4=8/11 ∴ BC = 8/11×15.4 = 11.2
Question. In Fig. 4.23, ABD is a triangle right-angled at A and AC ^ BD. Show that
(i) AB2 = BC . BD (ii) AD2 = BD . CD (iii) AC2 = BC . DC
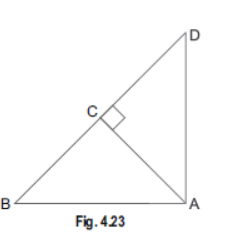
Sol. Given: ABD is a triangle right-angled at A and AC ^ BD.
To prove: (i) AB2 = BC . BD
(ii) AD2 = BD . CD
(iii) AC2 = BC . DC
Proof: (i) In ΔACB and ΔDAB, we have
∠ACB = ∠DAB = 90°
∠ABC = ∠DBA = ∠B (Common)
∴ ΔACB ~ ΔDAB (By AA criterion of similarity)
∴ BC/AB=AB/DB
AB2 = BC x BD
(ii) In ΔACD and ΔBAD, we have
∠ACD = ∠BAD = 90°
∠CDA = ∠BDA = ∠D (Common)
∴ ΔACD ~ΔBAD (By AA criterion of similarity)
∴ AD/BD=CD/AD
AD2 = BD x CD
(iii) We have DACB ~DDAB
⇒ ΔBCA ~ΔBAD …(i)
and ΔACD ~ΔBAD …(ii)
From (i) and (ii), we have
ΔBCA ~ΔACD
⇒ BC/AC=AC/DC
⇒ AC2 = BC. DC
Question. If AD and PM are medians of triangles ABC and PQR respectively, where ΔABC ~ΔPQR, prove that
AB/PQ=AD/PM
Sol. In ΔABD and ΔPQM, we have∠B = ∠Q (Q ΔABC ~ΔPQR) …(i)
AB/PQ=BC/QR (Q ΔABC ~ΔPQR)
⇒ AB/PQ=(1/2)BC/(1/2)QR
⇒ AB/PQ=BD/QM = [Since AD and PM are the medians of DABC and DPQR respectively] …(ii)
From (i) and (ii), it is proved that
ΔABD ~ΔPQM (By SAS criterion of similarity)
AB/PQ=BD/QM=AD/PM ⇒ AB/PQ=AD/PM
Question. ABC is a triangle in which AB = AC and D is a point on AC such that BC2 = AC x CD. Prove that BD = BC.
Sol. Given: DABC in which AB = AC and D is a point on the side AC such that BC2 = AC x CD
To prove: BD = BC
Construction: Join BD
Proof: We have, BC2 = AC x CD
Þ BC/CD=AC/BC …(i)
Thus, in DABC and DBDC, we have
AC/BC =BC/CD [From (i)]
and ∠C = ∠C [Common]
∴ ΔABC ~ΔBDC
Þ AB/BD=BC/CD …(ii)
From (i) and (ii), we get
AC/BC=AB/BD
∴ BD = BC (Q AB = AC)
Question. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Sol. Let ΔABC and ΔPQR be two similar triangles. AD and PM are the medians of DABC and DPQR respectively.
To prove:
ar(ΔABC )/ar(ΔPQR)=AD2/PM2
Proof: Since DABC ~DPQR
∴ ar(ΔABC )/ar(ΔPQR)=AB2/PQ2 …(i)
In ΔABD and ΔPQM
AB/PQ=BD/QM (Q AB/PQ=BC/QR=BC/QR)
and ∠B = ∠Q (Q ΔABC ~ΔPQR)
Hence, ΔABD ~ ΔPQM (By SAS Similarity criterion)
∴ AB/PQ=AD/PM …(ii)
From (i) and (ii), we have
ar(ΔABC )/ar(ΔPQR)=AD2/PM2
2. State whether the following statements are true or false. Justify your answer.
(i) If DE/PQ=EF/PR and ÐD= ÐQ, then DDEF ~DPQR.
(ii) P and Q are the points on the sides DE and DF of a triangle DEF such that DP = 4 cm, PE= 14 cm, DQ = 6 cm and DF= 21 cm. Then PQ||EF.
Sol. (i) False
(ii) False
3. (i) In Fig. 4.76, DE||AC and DF||AE. Prove that BF/FE=BE/EC .
(ii) Diagonals of a trapezium PQRS intersect each other at the point O, PQ||RS and PQ = 3RS. Find the ratio of the areas of triangles POQ and ROS.
Sol. (ii) 9 : 1
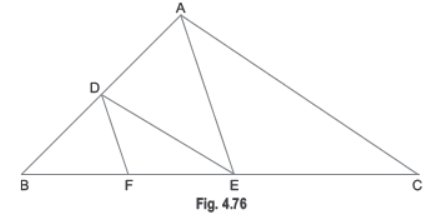
Question. In the given figure PQ ll BA; PR ll CA.

Solution. In ΔBRD,
BR ll PQ
Therefore,by basic proportionality theorm,

Question. Prove that the area of the equilateral triangle described on the side of an isosceles right angled triangle is half the area of the equilateral triangle described on its hypotenuse.
Solution. Given: In ΔABC in ∠ABC = 90° which and AB = BC.
Also, ΔABD and ΔACE are equilateral triangles.

Since,the ratio of the area of two similar triangles is equal to the square of ratio of their corresponding sides.
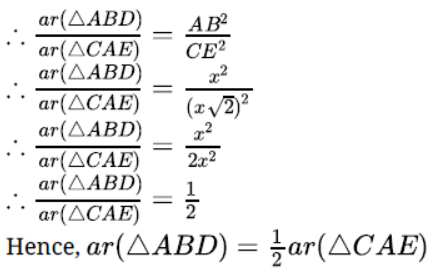
Question. In an isosceles triangle ABC, if AB =AC= 13 cm and the altitude from A on BC is 5 cm, find BC.
Solution. In ΔADB, by pythagoras theorem,

AD2 + BD2 = AB2
⇒ 52 + BD2 = 132
⇒ 25 + BD2 = 169
⇒ BD2 = 169 – 25 = 144
⇒ BD = √144= 12 cm
In ΔADB and ΔADC
∠ADB = ∠ADC [Each 90°]
AB = AC [Each 13 cm]
AD = AD [Common]
Then, ΔADB ≅ ΔADC [By RHS condition]
∴ BD = CD = 12 cm [By c.p.c.t]
Hence, BC = 12 + 12 = 24 cm.
Question. Let ΔABC ∼ ΔDEF. If ar ( ABC) = 100 cm , ar ( DEF) = 196 cm2 and DE = 7, then find AB.
Solution.

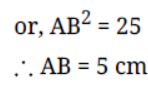
Question. In a trapezium ABCD, diagonals AC and BD intersect at O. If AB = 3CD, then find ratio of areas of triangles COD and AOB.
Solution. In Δ A O B and Δ C O D
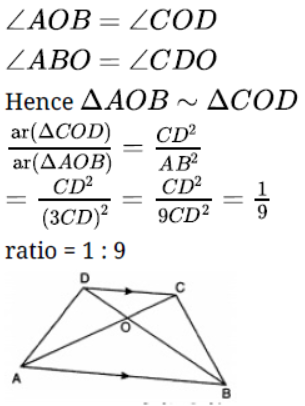
Question. ABC is an isosceles triangle with AB = AC and D is a point on AC such that BC2 = AC x CD. To prove: BD = BC.
Solution. To prove: BD = BC
proof:BC2 = AC x CD

Question. In an equilateral triangle ABC, D is a point on the side BC such the BD = 1/3 BC . Prove that 9AD2 = 7AB2 .
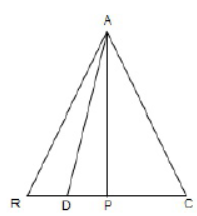
Solution. Given in ΔABC which AB = BC = CA and BD = 1/3BC .
Construction : Draw AP ⊥BC

Question. ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
Solution. We have,
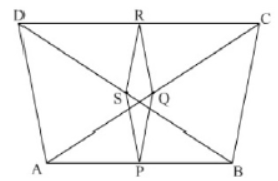
In ΔBAD, by mid-point theorem
PS||AD and PS = 1/2 AD ….(i)
In ΔCAD, by mid-point theorem
QR||AD and QR = 1/2 AD ….(ii)
Compare (i) and (ii)
PS || QE and PS = QR
Since one pair of opposite sides is equal as well as parallel then, PQRS is a parallelogram ….(iii)
Now, In ΔABC, by mid-point theorem,
PQ||BC and PQ = 1/2 BC ….(iv)
and, AD = BC …(v) [Given]
Compare equations (i)(iv) and (v)
PS = PQ ….(vi)
From (iii) and (vi),
Since, PQRS is a parallelogram with PS = PQ then PQRS is a rhombus.
Question. State whether the pairs of triangles in the figure are similar or not. Write the similarity criterion used for answering the question and also write the pairs of similar triangles in the symbolic form.
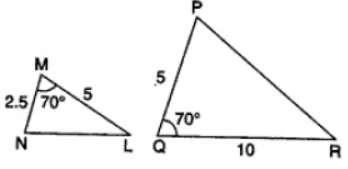
Solution.

Question. In Fig. DEFG is a square and ∠BAC = 90°. Prove that ΔAGF ∼ ΔEFC .
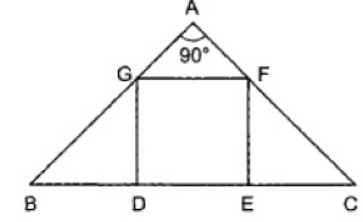
Solution. In ΔAGF and ΔEFC, we have

Question. In Fig. DE ll BC . Then, find AC.
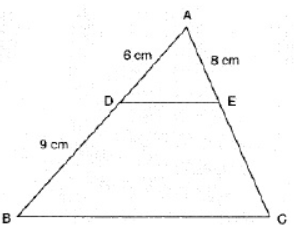
Solution. From figure,

Question. If ΔABC and ΔDEF are triangles such that AB/DE = BC/EF = AC/DF = 4/7 . Find areaΔABC/areaΔDEF .
Solution.
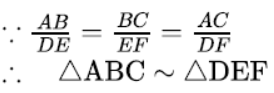
Since for similar triangles,the ratio of the areas is the square of their corresponding sides.

Question. If ∠P = ∠RTS , Then show that ∠PQR = ∠RTS .
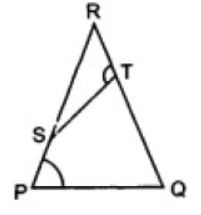
Solution. In RPQ and RTS

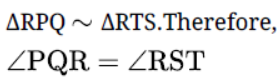
Question. Two triangles DEF and GHK are such that D = 48° and H = 57°. If ΔDEF ~ ΔGHK then find the measure of ∠F .
Solution. Given that ΔDEF ΔGHK.
∠D = G=48o …..(Given)
∠E = H=57o …..(Given)
In ΔDEF,
∠D+ ∠E+ ∠F=180o …(Angle sum property)
⇒ 48o +57o+ ∠F=180o
⇒ ∠ F=75o
Question. In Fig. ∠BAC = 90° , AD is its bisector. If DE ⊥ AC , prove that DE x (AB + AC) = AB + AC .
Solution. To prove the given result,we will use the following theorm.
The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle Since AD is the bisector of ∠A of ΔABC.


Question. If the diagonals of a quadrilateral divide each other proportionally, then it is a trapezium.
OR
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/DO Show that ABCD is a trapezium.

Solution. Through O, draw OE parallel to AB intersecting BC at E.
Now, in ΔABC, OE || AB (Δ by construction)
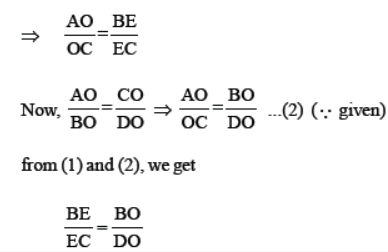

Question. In the given figure, P is the mid-point of BC and Q is the mid point of AP. If BQ when produced meets AC at R, prove that RA = 1/3 CA.
Solution. Draw PS || BR, meeting AC at S.
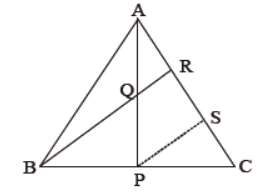
In ΔBCR, P is the mid-point of BC and PS || BR.
∴ S is the mid-point of CR.
⇒ CS = SR …(1)
In ΔAPS, Q is the mid-point of AP and QR || PS.
∴ R is the mid-point of AS.
⇒ AR = RS
from (1) and (2), we get
AR = RS = SC
Now, AC = AR + RS + SC= 3AR
⇒ AR= 1/3 CA Hence proved.
Question. In the given figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
(i) ΔAEP ~ ΔCDP (ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB (iv) ΔPDC ~ ΔBEC
Solution. (i) In ΔAEP and ΔCDP, we have
∠AEP = ∠CDP (each = 90°)
∠APE = ∠CPD (vertically opposite angles)
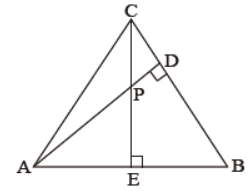
⇒ ∠AEP ~ ∠CDP (AA similarity criterion)
(ii) In ΔABD and ΔCBE, we have
∠ADB = ∠CEB (each = 90°)
∠ABD = ∠CBE (common)
⇒ ∠ABD ~ ∠CBE (AA similarity criterion)
(iii) In ΔAEP and ΔADB, we have
∠A = ∠A (common)
∠AEP = ∠ADB (each = 90°)
⇒ ∠AEP ~ ∠ADB (AA similarity criterion)
(iv) In ΔPDC and ΔBEC, we have
∠PCD = ∠BCE (common)
∠CDP = ∠CEB (each = 90°)
⇒∠PDC ~ ∠BEC (AA similarity criterion)
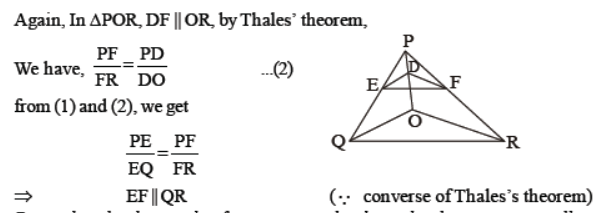
Question. In the given figure, DE || OQ and DF || OR. Prove that EF || QR.
Solution. In ΔPOQ, DE || OR, by Thales’ theorem,

Question. In an equilateral triangle ABC, D is a point on side BC such that BD= 1/3 BC. Prove that 9AD2 = 7AB2.
Solution. Draw AP ⊥ BC.

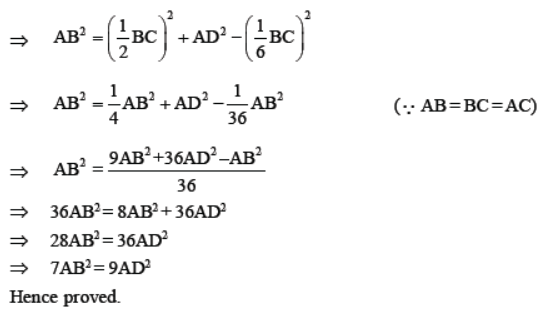
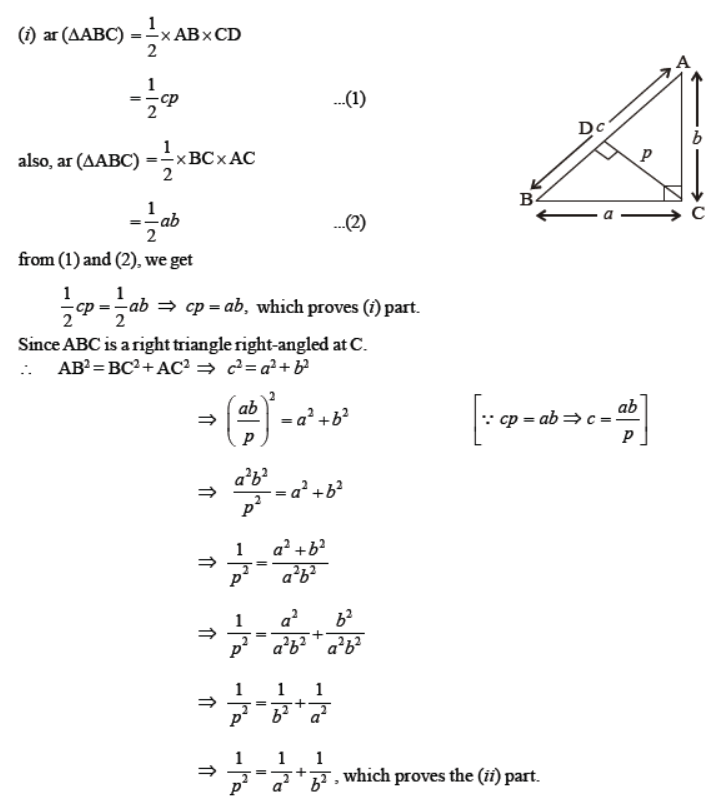
Question. ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that :
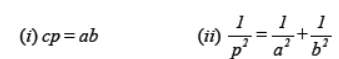
Solution.
Question. Prove that the diagonals of a trapezium divide each other proportionally.
OR
ABCD is a trapezium such that AB || DC. The diagonals AC and BD intersect at O. Prove that AO/BO = CO/DO
Solution. Through O, draw OE || CD (or AB). In ΔABD, EO || AB, by Thales’ theorem,
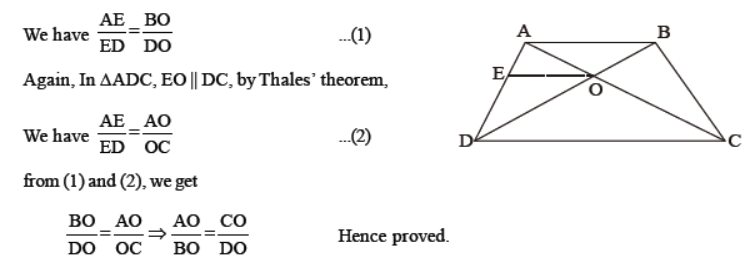
Question. In the given figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Solution. (i) In right ΔOFA, ΔODB and ΔOEC,
using Pythagoras theorem, we have
OA2 = AF2 + OF2
OB2 = BD2 + OD2
OC2 = CE2 + OE2
Adding (1), (2) and (3), we get
OA2 + OB2 + OC2 = AF2 + BD2 + CE2 + OF2 + OD2 + OE2
⇒ OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
which proves the (i) part.
(ii) In right ΔODB and ΔODC, we have
OB2 = OD2 + BD2
and OC2 = OD2 + CD2
⇒ OB2 – OC2 = BD2 – CD2 …(4)
Similarly, we have
OC2 – OA2 = CE2 – AE2 …(5)
and OA2 – OB2 = AF2 – BF2 …(6)
Adding (4), (5) and (6), we get
(OB2 – OC2)+ (OC2 – OA2) + (OA2 – OB2)= (BD2 – CD2) + (CE2 – AE2) + (AF2 – BF2)
⇒ 0 = (BD2 + CE2 + AF2) – (AE2 + CD2 + BF2)
⇒ AF2 + BD2 + CE2 = AE2 + CD2 + BF2 , which proves the (ii) part.
Question. CD and GH (D and H lie on AB and FE) are respectively bisectors of ∠ACB and ∠EGF and ΔABC ~ ΔFEG. Prove that : (i) CD/GH = AG/FG (ii)ΔDCB ~ ΔHGE (iii)ΔDCA ~ ΔHGF.
Solution. (i) Given ΔABC ~ ΔFEG
⇒ ∠A = ∠F
and ∠C = ∠G …(1)



Question. In the given figure, OA/OC = OD/OB . Prove that ∠A = ∠C and ∠B = ∠D
Solution. In ΔAOD and ΔCOB, we have

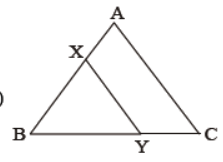
Question. In the given figure, XY || AC and XY divides triangular region ABC into two parts equal in area. 10
Determine AX/AB .
Solution. We have, XY || AC and ar (ΔBXY) = ar (quad. XYCA)
⇒ ar (ΔABC) = 2.ar (ΔBXY) …(1)
Now, XY || AC and BA is a transversal.
⇒ ∠BXY= ∠BAC …(2)
Thus, In ΔBAC and ΔBXY, we have
∠XBY = ∠ABC (common)
∠BXY = ∠BAC [from (2)]
⇒ ∠BAC ~ ∠BXY (AA similarity criterion)
Question. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1,1/2 hours?
Solution. Distance travelled by an aeroplane due north in 1,1/2 hours = 1000 X 3/2 km = 1500 km
∴ OA = 1500 km
Distance travelled by an aeroplane due west in 1,1/2 hours = 1200 X 3/2 km = 1800 km
∴ OB = 1800 km

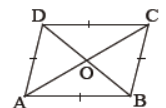
Question. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
OR
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2 = AC2 + BD2
Solution. Let the diagonals AC and BD of rhombus ABCD intersect at O. Since the diagonals of a rhombus
bisect each other at right angle.
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90° and AO = CO, BO = DO.
Since ΔAOB is a right triangle right-angled at O.
⇒ AB2 = OA2 + OB2 (using Pythagoras theorem)
Question. Two poles of height a metres and b metres are p metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by ab/a + b metres.
Solution. Let AB and CD be two poles of height a metres and b metres respectively such that poles are p metres apart. Let the lines AD and BC meet at O such that OE = h metres.

Question. Prove that area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonal.
Solution. Let ABCD be the given square. Equilateral triangles ΔBCE and ΔACF are described on side BC and diagonal AC respectively.

Since ΔBCE and ΔACF are equilateral they are equiangular and hence ΔBCE ~ ΔACF (AAA similarity criterion)

PRACTICE EXERCISE
Question. The perimeters of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm, find AB.
Solution. AB = 15 cm
Question. D and E are points on the sides AB and AC respectivley of a ΔABC such that DE || BC and divides ΔABC into two parts, equal in area, find BD/AB .
Solution. 2 -√2/2
Question. In the given figure, AQ and PB are perpendiculars to AB. If AO = 10 cm, BO = 6cm and PB = 9 cm, find AQ.
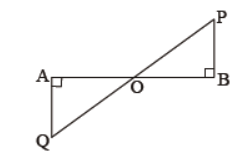
Solution. AQ = 15 cm
Question. Use the given figure to find the value of x if :
(i) OA = 4x – 2, OB = 4x + 1, OC = 2x + 2, OD = 3x – 1
(ii) OA = 3x – 1, OB = 2x + 1, OC = 5x – 3, OD = 6x – 5
Solution. (i) x = 5 (ii) x = 2 or x = 1/2
Question. In the given figure, ABC is a triangle, right angled at B. If FG || DE || CB and AG = GE = EB, find DE + FG.

Solution. 12 cm
Question. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance betwen their feet is 12 m, find the distance between their tops.
Solution. 13 m
Question. In the given figure, ΔEDC ~ ΔEBA, ΔBEC = 115° and ΔEDC = 70°. Find :
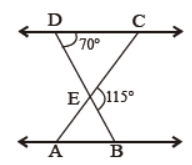
(i) ∠DEC
(ii) ∠DCE
(iii) ∠EAB
(iv) ∠AEB
(v) ∠EBA
Solution. (i) 65 (ii) 45° (iii) 45° (iv) 65° (v) 70°
Question. In the given figure, AO/OC = BO/OD = 1/2 and AB = 5 cm. Find DC.
Solution. 10 cm
Question. In ΔABC, DE is parallel to base BC, with D on AB and E on AC. If AD/DB = 2/3 , find BC/DE .
Solution. 5/2
Question. In the given figure, AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm. Find x and y.

Solution. x = 3.75 cm, y = 6.67 cm
Question. A ladder 25 m long reaches a window which is 24 m above the ground on side of the street. Keeping the foot at the same point, the ladder is turned to the other side of the street to reach a window 7 m high. Find the width of the street.
Solution. 31 m
Question. In ΔABC, P divides the side AB such that AP : PB = 1 : 3. Q is a point on AC such that PQ || BC. Find the ratio of the areas of ΔAPQ to trapezium BPQC.
Solution. 1 : 3
Question. In the given figure, DE || BC and AD : DB = 5 : 4. Find ar (ΔDFE)/ar (ΔCFB).
Solution. 25 : 81
Question. A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
Solution. 1.6 m
Question. D and E are points on the sides AB and AC respectively of ΔABC such that DE is parallel to BC and AD : DB = 4:5. CD and BE intersect each other at F. Find the ratio of the areas of ΔDEF and ΔBCF.
Solution. 16 : 81
Question. In the given figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8cm and AD = 4 cm, find CD.
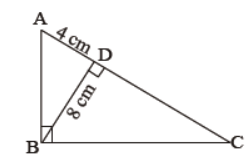
Solution. CD = 16 cm
Question. The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude of the bigger triangle is 5 cm, find the corresponding altitude of the other.
Solution. 3.5 cm
Question. In the given figure, DE || BC and AD/DB = 3/5 . If AC = 4.8 cm, find AE.

Solution. 1.8 cm
Question. In the given figure, D is a point on AB and E is a point on AC of ΔABC such that DE || BC. If AD : DB = 1:2, AB = 18 cm and AC = 30 cm, find the values of AE, EC, AD and DB.
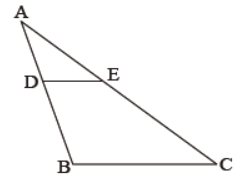
Solution. AE = 10 cm, EC = 20 cm, AD = 6 cm and DB = 12 cm
Question. In the given figure, PQ || RS. Find PT and QT.

Solution. PT = 4.8 cm, QT = 5.7 cm
Question. The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
Solution. 8.8 cm
Question. ABCD is a trapezium in which AB || DC and AB = 2DC. Determine the ratio of the areas of ΔAOB and ΔCOD.
Solution. 4 : 1
Question. In the given figure, find the value of x if DE || AB.
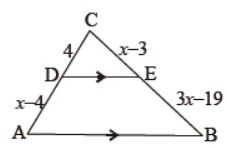
Solution. x = 8 or 11
Question. In the trapezium ABCD, AB || CD and AB = 2CD. If the area of ΔAOB = 84 cm2, find the area of ΔCOD.
Solution. 21 cm2
Question. In the given figure, DE || BC, AD = 2 cm, BD = 2.5 cm, AE = 3.2 cm and DE = 4 cm. Determine AC and BC.
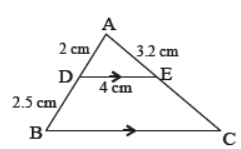
Solution. AC = 7.2 cm, BC = 9 cm
Question. A ladder 25 m long reaches a window of a building 20 m above the ground. Determine the distance of the foot of the ladder from the building.
Solution. 15 m
Question. A vertical stick 15 m long casts its shadow 10 m long on the ground. At the same time, the flag pole casts a shadow 60 m long. Find the height of the pole.
Solution. 72 m
Question. The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Solution. 13 cm
Question. In the given figure, find x in terms of a, b and c.

Solution. x = ac/b + c
Question. In the given figure, ABC is a right triangle right-angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD = 3√5/2 cm Find the length of CE.
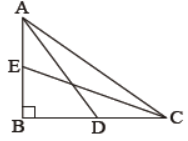
Solution. 2√5 cm
Question. In the given figure, ABCD is a square. F is the mid-point of AB, BE is one-third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.

Solution. 12√2 cm
Question. In the given figure, DE || BC and DE : BC = 4 : 5. Find ratio of the areas of ΔADE and trapezium BCED.
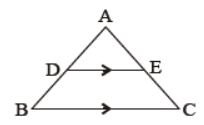
Solution. 16 : 9
Question. In the given figure, AB || QR. Find PB.
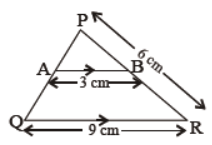
Solution. PB = 2 cm
Assignments for Class 10 Mathematics Triangles as per CBSE NCERT pattern
All students studying in Grade 10 Mathematics Triangles should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Triangles exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Triangles which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.
Some advantages of Free Assignments for Class 10 Mathematics Triangles
- Solving Assignments for Mathematics Triangles Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
- By solving one assignments given in your class by Mathematics Triangles teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
- You will be able to understand the type of questions which are expected in your Mathematics Triangles class test
- You will be able to revise all topics given in the ebook for Class 10 Mathematics Triangles as all questions have been provided in the question banks
- NCERT Class 10 Mathematics Triangles Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
- Parents will be able to take print out of the assignments and give to their child easily.
All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Triangles teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Triangles Assignments PDF.

You can download free assignments for class 10 Mathematics Triangles from https://www.assignmentsbag.com
You can get free PDF downloadable assignments for Grade 10 Mathematics Triangles from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided assignments for all subjects in Grade 10, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge
Yes all test papers for Mathematics Triangles Class 10 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.
https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.


