Assignments for Class 10 Mathematics Surface Area and Volume have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Surface Area and Volume from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Surface Area and Volume. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Surface Area and Volume book and get good marks in class 10 exams.
Question. A metallic solid cone is melted to form a solid cylinder of equal radius. If the height of the cylinder is 6 cm, then the height of the cone was
(a) 10 cm
(b) 12 cm
(c) 18 cm
(d) 24 cm
Answer
C
Question. The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be 1/27 of the volume of the given cone, then the height above the base at which the section has been made is
(A) 10 cm
(B) 15 cm
(C) 20 cm
(D) 25 cm
Answer
C
Question. The number of solid spheres, each of diameter 6 cm that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm is
(A) 3
(B) 4
(C) 5
(D) 6
Answer
C
Question. A right triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side of 3 cm to form a cone.
The volume of the cone so formed is
(A) 12π cm3
(B) 15π cm3
(C) 3 16π cm
(D) 20π cm3
Answer
C
Question. If the areas of three adjacent faces of a cuboid are x, y, z respectively, then the volume of cuboid is
(A)xyz
(B) 2xyz
(C) xyz
(D) 3 xyz
Answer
C
Question. The length of the longest pole that can be kept in a room (12m × 9m × 8m) is
(A)29 m
(B) 21 m
(C)19 m
(D)17 m
Answer
D
Question. A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top.
The height of the cone is h. If the total volume of the solid is 3times the volume of the cone, then the height of the circular cylinder is
(A) 2h
(B) 2h/3
(C) 3h/2
(D) 4h
Answer
B
Question. The volume of a sphere (in cu. cm) is numerically equal to its surface area (in sq. cm). The diameter of the sphere (in cm) is
(A) 3
(B) 6
(C) 2
(D) 4
Answer
B
Question. The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
(A) 9.7 cm3
(B) 77.6 cm3
(C) 58.2 cm3
(D) 19.4 cm
Answer
D
Question. The ratio between the volumes of two spheres is 8:27. What is the ratio between their surface areas?
(A) 2:3
(B) 4:5
(C) 5:6
(D) 4:9
Answer
D
Question. The height of a conical tent is 14 m and its base area is 346.5 m2. How much canvas, 1.1 wide, will be required for it?
(A) 490 m
(B) 525 m
(C) 665 m
(D) 860 m
Answer
B
Question. If four times the sum of the areas of two circular faces of a cylinder of height 8 cm is equal to twice the curved surface area, then diameter of the cylinder is
(A) 4 cm
(B) 8 cm
(C) 2 cm
(D) 6 cm
Answer
B
Question. The ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube is
(A) π : 8
(B) π : 6
(C) 8 : π
(D) 6 : π
Answer
D
Question. If a cone is cut into two parts by a horizontal plane passing trough the mid-points of its axis, the ratio of the volumes of the upper part and the cone is
(A) 1 : 2
(B) 1 : 4
(C) 1 : 6
(D) 1 : 8
Answer
D
Question. 12 spheres of the same size are made from melting a solid cylinder of diameter 16 cm and 2 cm height. The diameter of each sphere is
(A) √3cm
(B) 2 cm
(C) 3 cm
(D) 4 cm
Answer
B
Question. The ratio between the radius of the base and the height of the cylinder is 2:3, If its volume is 1617 cm3, the total surface area of the cylinder is
(A) 308 cm2
(B) 462 cm2
(C) 540 cm2
(D) 770 cm2
Answer
D
Surface Areas and Volumes
Surface Areas of Combination of Solids
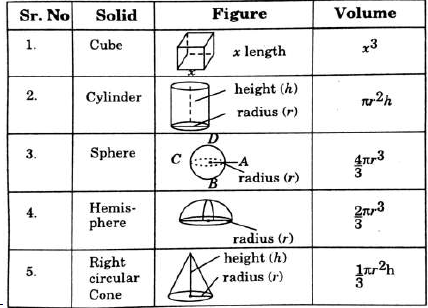
We can calculate the surface area of an object formed by combining any two of the basic solids, namely cuboid, cone, cylinder, sphere and hemisphere. Here are the steps :
- Break the given object in known basic shapes of solids.
- Total surface area of the new solid is the sum of the curved surface areas of each of the individual parts.
Example : Total surface area (TSA) of the given object A = Curved surface area of cylinder + curved surface area of cone F
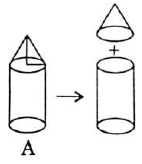

Frustum of a Right Circular Cone : Given a right circular cone, which is sliced through by a plane parallel to its base, when the smaller conical portion is removed, the resulting solid is called a Frustum of a Right Circular Cone. F
Volume of Combination of Solids: we can find the volume of objects formed by combining any two of a cuboid, cone, cylinder, sphere and hemisphere.
Conversion of one solid to another solid : When we convert one solid to another (we do this in liquid form by melting the solid) . The volume remain constant. So knowing the volume formula of converted object we can calculate its other parameters like height,redius etc.
CSA (curved surface area), TSA (total surface area) and volume of a frustum of a cone.
Note : let h be the height, l be the slant height ,r1 and r2 be radii of the ends (r1>r2 ) of a frustum of a cone. Formulae for the volume of frustum, the curved surface area and total surface area of the frustum are as given below.

Question. Find the area of the triangle whose base measures 24 cm and the correspondingheight measures 14.5 cm.
Solution.

Question. A metallic right circular cone 20 cm high and whose vertical angel is 60° is cut into two parts at the middle of its height by a plane parallel to its base if the frustum so obtained be drawn into a wire of uniform diameter 1/16 cm, find the length of the wire.
Solution.

According to the question,A metallic right circular cone 20 cm high and whose vertical angel is 60° is cut into two parts at the middle of its height by a plane parallel to its base if the frustum so obtained be drawn into a wire of uniform diameter 1/16 cm.
Total height of cone = 20 cm and Vertex angle = 30°
Let the radius of cone be r2 .
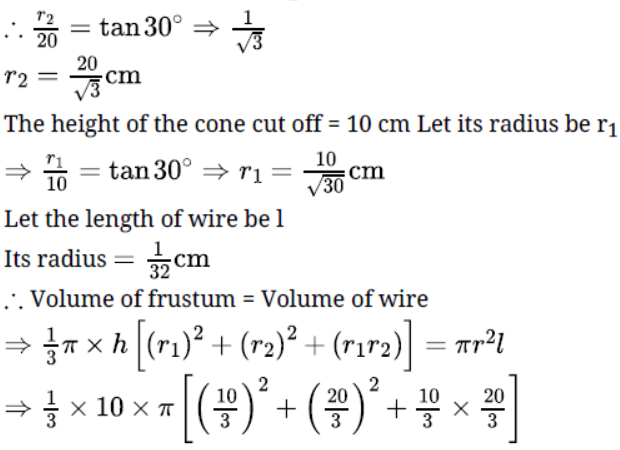
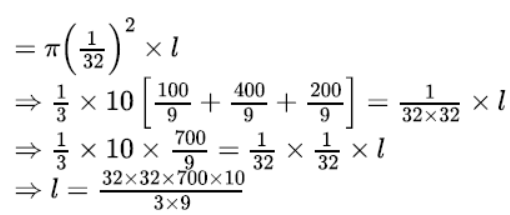
= 796444.4 cm.
Hence, the length of wire = 7964.44 m
Question. A solid metallic sphere of diameter 8 cm is melted and drawn into a cylindrical wire of uniform width. If the length of the wire is 12 m, find its width.
Solution. The diameter of the sphere = 8 cm
Radius of the sphere = 4 cm
Length of the wire = 12 m = 1200 cm
Volume of the sphere = Volume of the cylindrical wire
The width of the wire = the diameter of the base of the wire

Question. A circus tent is in the shape of a cylinder surmounted by a conical top of same diameter If there common diameter is 56 m, the height of cylindrical part is 6 m and the total height of the tent above the ground is 27 m, find the area of canvas used in the tent.
Solution. Total height of tent = 27 m
Height of cylindrical part = 6 m
∴ Height of conical part = 27 – 6 = 21 m

Question. If the volumes of two spheres are in the ratio 64 : 27,then find the ratio of their surface areas.
Solution. Let the radius of 1st sphere be ‘r1‘
Let the radius of 2nd sphere be ‘r2‘
According to question,
Ratio of the volume of the given spheres is,

Question. A right triangle whose sides are 15 cm and 20 cm is made to revolve about its hypotenuse. Find the volume and the surface area of the double cone so formed. (Use π= 3.14)
Solution.


Question. Water in a canal, 30 dm wide and 12 dm deep is flowing with velocity of 10km/hr. How much area will it irrigate in 30 minutes, if 8 cm of standing water is required for irrigation?
Solution. Width of the canal = 30 dm = 300 cm = 3 m
Depth of the canal 12 dm = 120 cm = 1.2 m
It is given that the water is flowing with velocity 10 km/hr
Therefore Length of the water column formed in 1/2 hour = 5 km = 5000 m
Therefore, volume of the water flowing in 1 hour
= Volume of the cuboid of length 5000 m, width 3 m and depth 1.2 m
10 x 30/60 km = 5km = 500 m
⇒ Volume of the flowing water in half hour = 5000 x 1.2 x 3m3
Suppose x m2 area is irrigated in 1/2 hour
x × 8 /100 = 18000
x = 1800000/8
x = 225000
Question. A reservoir in the form of the frustum of a right circular cone contains 44 x 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take: = 22/7)
Solution. Volume of water in frustum = 44 x 107 litres
= 44 x 104 litres
= 440000 m3
Radius of bottom of frustum = 50 m(r)
Radius of top of frustum = 100 m (R).
Let the depth of water = h (m) = height of frustum
Let slant height = 1 cm

Question. A cylindrical bucket, 32 cm high and with a radius of base 18 cm, is filled with sand.
This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution. For cylindrical bucket
Radius of base (r) = 18 cm
Height (h) = 32cm

Hence, the radius of the heap is 36 cm
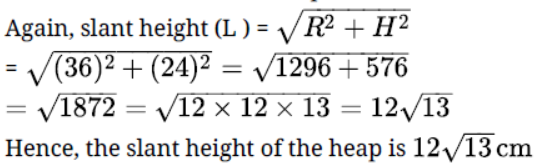
Question. The rain water from a roof of 44 m x 20 m drains into a cylindrical tank having diameter of base 4 m and height 3.5 m. If the tank is just full, find the rainfall in cm.
Solution. Length of the roof (l) = 44 m,
Breadth of the roof (b) = 20 m
Let the height of the water on the roof be h m.
Volume of water falling on the roof = l x b x h
= 44 20 h
= 880h
Radius of the cylindrical vessel (R) = 4/2 = 2m
Height of the water in the cylindrical vessel (H) = 3.5 m
Volume of the water in the cylindrical vessel = πR2H
= 22/7 x 2 x 2 x 3.5
= 308/7
= 44
Volume of water falling on the roof = Volume of the water in the cylindrical vessel
⇒ 880 h = 44
⇒ h = 44/880
⇒ h = 44/880 x 100
⇒ h = 5 cm
⇒ Height of the water on the roof is 5 cm.
Question. The surface area of a sphere is 616 cm2. Find its radius.
Solution. Surface area of a sphere = 616 cm2.

Practice Exercise :
Question. A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the sphere is 14cm and the total height of the vessel is13cm. Find its capacity?
Solution. 1642.67cm³
Question. A solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2cm and the total height of the toy is 10.2cm. Find the volume of the wooden toy.
Solution. 266.12cm³
Question. A tent is of the shape of a right circular cylinder up to a height of 3m and then becomes a right circular cone with a maximum height of 13.5m, above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs.2 per sq. metre, if the radius of the edge is14 metres.
Solution. Total area 1034m², Cost of painting Rs.2068
Question. A cylinder and a cone are of the same base radius and of the same height. Find the ratio of the curved surface area of the cylinder to that of cone.
Solution. √2:1
Question. A circus tent is cylindrical up to a height of 3m and conical above it. If the diameter of the base is 105 m and the slant height of the conical part is 53m. Find the total canvas used in making the tent.
Solution. 9735m²
Question. A bucket is in the form of frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28cm and 21cm respectively. Find the height of the bucket.
Solution. Height 15cm
Question. A pen stand made of wood is in the shape of a cuboid with four conical depression’s to hold pens. The dimensions of the cuboid are 15cm by 10cm by 3.5cm. The diameter of each of the depression is 1cm and the depth is 1.4cm. Find the volume of the wood in the entire stand.
Solution. 523.53 cm3
Question. Three cubes each of side 5cm are joined end to end. Find the surface area of the resulting cuboid.
Solution. 350 cm2
Question. The diameter of a metallic sphere is 6cm. The sphere is melted and drawn into a wire of uniform crosssection. If the length of the wire is 36m. Find its radius.
Solution. 1mm
Question. A cylinder and a cone are of the same base radius and of the same height. Find the ratio of the curved surface area of the cylinder to that of cone.
Solution. √2:1
Question. A circus tent is cylindrical up to a height of 3m and conical above it. If the diameter of the base is 105 m and the slant height of the conical part is 53m. Find the total canvas used in making the tent.
Solution. 9735m²
Question. If the diameter of cross-section of a wire is decreased by 5%. How much percent will the length be increased so that the volume remains the same?
Solution. 10.8%
Question. The perimeters of the ends of a frustum is48cm and 36cm.If the height of the frustum be 11cm, find its volume.
Solution. 1554cm³
Question. Find the curved surface area of a right circular cone of height 15 cm and base diameter is16cm.
Solution. 427.04 cm²
Question. Find the maximum volume of a cone that can be out of a solid hemisphere of radius r.
Solution. 1/3 π r³
Question. Two cubes of volume 64cm3 are joined end to end. Find the volume of the sphere.
Solution. 128cm³
Question. A toy is in the form of a cone mounted on a hemisphere. The diameter of the base of the cone is 7 cm and its height is 15.5 cm. Find the volume of the toy. (Use = 3.14).
Solution. According to question it is given that Diameter of the base of the cone is = 7cm
Therefore radius = 7/2 = 3.5cm
Total height of the toy = 14.5 cm
Height of the cone = 15.5 – 3.5 = 12 cm
Height of the hemisphere = 3.5 cm
According to question it is also given that
Volume of the toy = Volume of cone + Volume of hemisphere
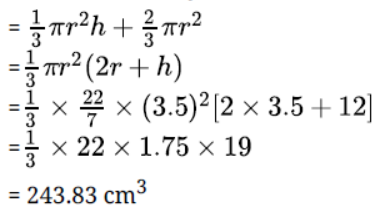
Question. Find the length of the diagonal of a square whose area is 128 cm2. Also, find its perimeter.
Solution.

Question. A cone of height 24 cm and radius of base 6 cm is made up of modeling clay. Find the volume of the cone.
Solution. h = 24cm, r = 6cm
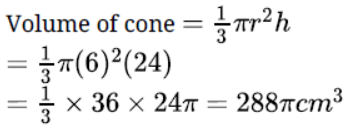
Question. The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. Find the slant height of the bucket. 8
Solution. Given,r1 = 24 cm, r2 = 15 cm, h = 40 cm
We know that, slant height of bucket is given by:-

Question. A vessel is in the form of a hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. [Use π = 22/7]
Solution. Radius of hemispherical portion = radius of cylindrical portion, π = 14/2 = 7 cm

Height of cylinder, h = 13 – 7 = 6 cm
Total Surface area of vessel = Curved surface area of hemisphere + Curved surface area of cylinder
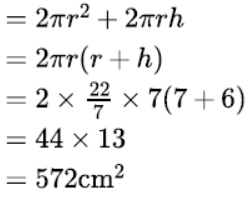
Question. 50 circular plates each of radius 7 cm and thickness 5 mm are placed one above another to form a solid right circular cylinder. Find the total surface area of the cylinder so formed.
Solution. Clearly, we have
radius of the cylinder so formed, r = 7 cm, and
height of the cylinder so formed, h = (50 x 5) mm
= 250 mm = 25 cm.
∴ total surface area of the cylinder so formed

Question. A friction clutch is in the form of a frustum of a cone, the diameter of the ends being 32 cm and 20 cm and length 8 cm. Find its bearing surface and volume.
Solution. Let ABB ‘A’ be the friction clutch of slant height l cm.

Question. A hemispherical depression is cut out from one face of a cubical block of side 7 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid.
Solution. Edge of the cube, a = 7 cm.

Radius of the hemisphere, r = 7/2 cm.
= total surface area of the cube – area of the top of hemispherical part + curved surface area of the hemisphere
Surface area of remaining solid
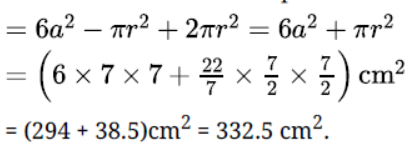
Question. The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Solution. Side of cube = 10.5 cm
The largest sphere is carved out from this cube
Then, the diameter of sphere = 10.5 cm
∴ radius of sphere = 10.5 /2 cm

Question. A spherical ball of lead 3 cm in diameter is melted and recast into three spherical balls. The diameters of two of these balls are 1 cm and 1.5 cm. Find the diameter of the third ball.
Solution.

Question. Water flows at the rate of 10 m per min. through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm?
Solution.

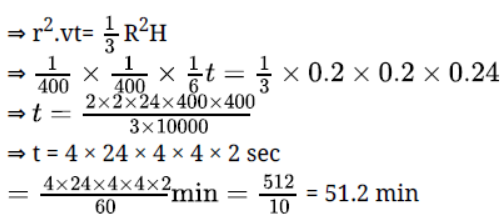
= 51 min + 0.2 min = 51 min + 0.2 × 60sec
⇒ t = 51 min and 12 sec.
Hence, conical tank will fill in 51 min and 12 sec.
Question. The height of a solid cylinder is 15 cm. and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm, and height 4 cm are cut off. Find the volume of the remaining solid.
Solution. Given that diameter of cylinder = 7cm
Radius of cylinder (R) = cm
Also, Height of cylinder(H) = 15 cm
Let radius of conical hole = r = 3 cm
Height of conical hole = h = 4 cm
∴ Volume of remaining solid = volume of cylinder – 2 volume of conical hole
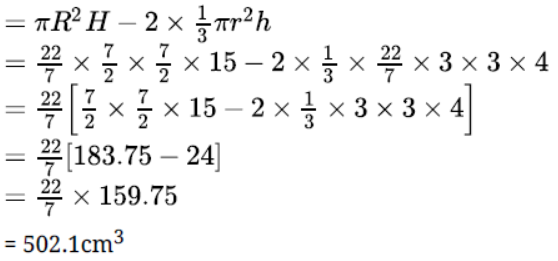
Therefore, the volume of remaining solid is 502.1 cm3
Question. Given that 1 cubic cm of marble weighs 25 g. The weight of a marble block 28 cm in width and 5 cm thick is 112 kg. Find the length of the marble block.
Solution. Total weight = 112 kg
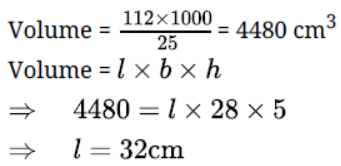
Question. Find the ratio of the volume of a cube to the volume of a sphere, if sphere fits completely inside the cube.
Solution. Since the sphere fits inside the cube, the diameter of the sphere is equal to the side of the cube.
Let the side of the cube =2r = diameter of the sphere
So, the radius of the sphere = r
Now, Volume of the cube: Volume of the sphere
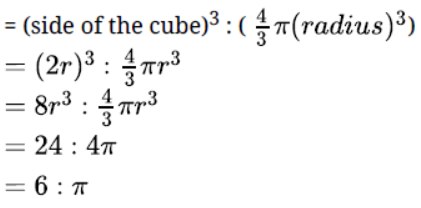
Question. Find the area of a triangle having base 25 cm and height 10.8 cm.
Solution.
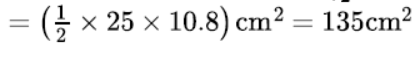
Question. The diameter of a copper sphere is 18 cm. It is melted and drawn into a long wire of uniform cross section. If the length of the wire is 108 m, find its diameter.
Solution. Diameter of copper sphere = 18 cm
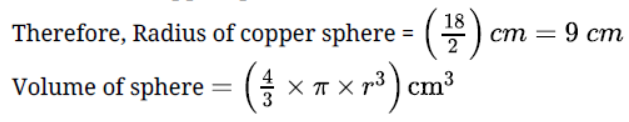

Question. Find the volume of a frustum of base radii 7 cm and 3.5 cm and height 2 cm.
Solution. R = 7 cm r = 3.5 cm h = 2 cm

Question. An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar, if one cubic cm of iron weighs 10 g.
Solution. Let us suppose that r denotes the radius of the cylinder = 8 cm.

Suppose R denotes the radius of the cone = 8 cm.
Let h be the height of the cylinder = 240cm.
Suppose H is the height of the cone = 36 cm.
Total volume of the iron = volume of the cylinder + volume of the cone
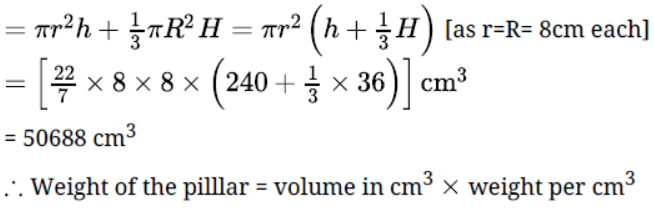
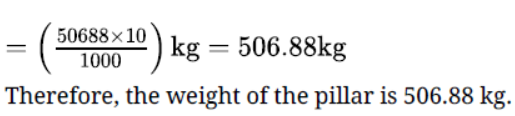
Question. The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
Solution. Diameter of sphere = 42 cm

Hence length of the wire is 63 m.
Question. Due to heavy floods in a state , thousands were rendered homeless . 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the government and decided to share their whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m , with conical upper part of same radius but of height 2.1 m . If the canvas used to make the tents cost 120 Rupees / sq. metre , then find the amount shared by each school to set up tents . What value is generated by the above problem?
Solution. Radius of cylindrical part and cone part of tent, r = 2.8m
height of cylindrical part of tent, H = 3.5m
height of conical part of tent, h = 2.1m
Number of tents to be made = 1500
Cost of canvas for making tent = 120 rupees/sq.m
Number of school = 50
Canvas required for one tent = Curved surafce area of cylinder + Curved surface of cone = 2πrh + πrl
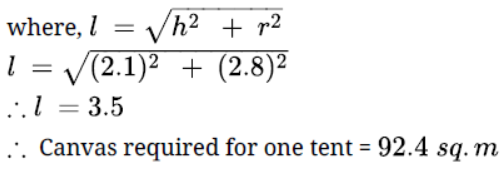
So, canvas required for 1500 tents = 1500 × canvas required for one tent.
= 92.4 × 1500 = 1,38,600 sq.m
Thus, cost of the canvas = 120 × canvas required for 1500 tents = Rs 1,66,32,000
Hence, amount shared by each school = cost /50 = 16632000 / 50 = Rs 332640
Values schools feel their responsibility for helping government in its efforts to face natural calamities like floods, etc. And, also want their students to be aware of the causes of such natural calamities and how we could help in such situation.
Question. Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
Solution. When two identical cones are joined base to base, the total surface area of new solid
becomes equal to the sum of curved surface areas of both the cones.
So, total surface area of solid = πrl + πrl = 2πrl
In two cones, r = 8 cm, h = 15 cm
Now, l2 = r2 + h2 = 82 + 152 = 64 + 225 = 289
⇒ l2 = (17)2
⇒ l = 17 cm
Total surface area of solid = 2πrl
= 2 × π × 8 × 17
= 272π cm2
= 854.857 cm2
Hence, the surface area of new solid = 854.857 cm2.
Question. A well of diameter 3 m is dug 14 m deep. The soil taken out of it is spread evenly around it to a width of 5 m. to form a embankment. Find the height of the embankment.
Solution. According to the question, A well of diameter 3 m is dug 14 m deep. The soil taken out of it is spread evenly around it to a width of 5 m. to form a embankment The volume of soil taken out from the well

Question. In a cylindrical vessel of diameter 24 cm, filled up with sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. Find the increase in height of water level.
Solution. Diameter of cylindrical vessel = 24 cm
Radius of cylindrical vessel = 24/2 = 12 cm
Let height of water level rise = h cm
Radius of ball = 6 cm
According to the question
Volume of spherical ball = Volume of water rise in cylinder
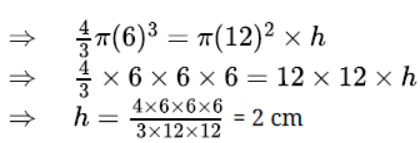
Question. A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
Solution.
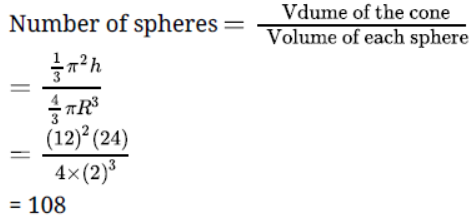
Question. Find the area of a rhombus whose diagonals are 48 cm and 20 cm long.
Solution.

Question. Four right circular cylindrical vessels each having diameter 21 cm and height 38 cm are full of ice cream. The ice cream is to be filled in cones of height 12 cm and diameter 7 cm having a hemispherical shape on the top. Find the total number of such cones which can be filled with ice cream.
Solution. According to question it is given that
Diameter of cylinder = 21 cm,
Therefore, radius of cylinder = 21/2 cm
Height of cylinder = 38 cm.
Therefore, Volume of four cylindrical vessels
= 4 x π (21/2)2 x 38 cm2
Dimensions of cone with hemispherical end:
Diameter of base of cone = diameter of hemisphere = 7 cm
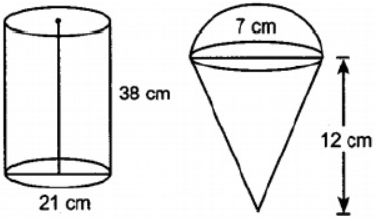
Height of cone = 12cm
Volume of one ice cream cone = volume of conical part + volume of hemispherical part

Hence, 216 cones can be filled.
Question. One iron solid is a cuboid of dimensions 30 cm x 30 cm x 42.6 cm. It is melted and cubes each of side 3 cm are moulded from it. Find the number of cubes formed.
Solution. Let n be the number of cones.
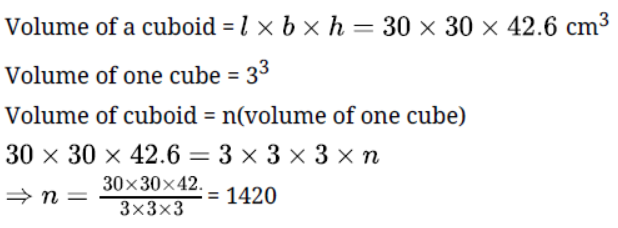
Question. A toy is in the form of a cone surmounted on a hemisphere of a common base of diameter 7 cm. If the height of the toy is 15.5 cm, find the total surface area of the toy.[Use π = 22/7 ]
Solution. It is given that a toy is in the form of a cone surmounted on a hemisphere of a
common base of diameter 7 cm. If the height of the toy is 15.5 cm, we have to find the total surface area of the toy.
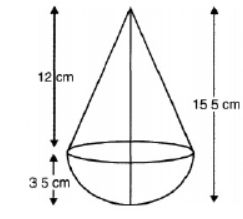
radius, r = 3.5 cm
height, h = 12 cm

Question. A sphere of maximum volume is cut out from a solid hemisphere of radius 6 cm. Find the volume of the cut out sphere.
Solution. A sphere with maximum volume that can be cut out from a solid hemisphere will be
the one whose diameter will be equal to that of the radius of the hemisphere
i.e, radius of the sphere = 1/2 radius of hemisphere = 3 cm
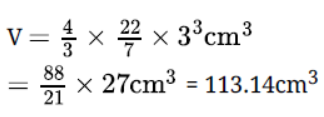
Question. A cone of height 24 cm has a curved surface area of 550 cm2. Find its volume.
Solution. Height of the cone = 24 cm
Let radius be r cm and slant height be l cm.

Question. A cubic cm of gold is drawn into a wire of 0.1 mm in diameter, find the length of the wire.
Solution. Given,
Volume of gold = 1 cm3 = 1000 mm3 ……(1)
Diameter of wire = 0.1 mm
Radius of wire = 0.1/2 = 0.05 mm
Let, the length of the wire = h mm
According to the question,
Volume of wire = Volume of gold

Question. The sides of a triangle are in the ratio 5:12:13, and its perimeter is 150 m. Find the area of the triangle.
Solution. According to question given sides are in the ratio of 5 : 12 : 13
On dividing 150 m in the ratio 5 : 12 : 13, we get

Question. A solid metallic sphere of diameter 16 cm is melted and recasted into smaller solid cones, each of radius 4 cm and height 8 cm. Find the number of cones so formed.
Solution. Diameter of sphere = 16 cm
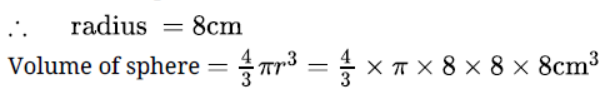

Question. A joker’s cap is in the form of a right circular cone of base radius 7 cm and the slant height is 25 cm. Find the area of the cap.
Solution. Base radius of Joker’s cap = 7 cm
Slant height = 25 cm

Question. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top which is open, is 5cm. It is filled with water upto the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of water flows out. Find the number of lead shots dropped into the vessel.
Solution. We have, height of the conical vessel, h = 8 cm and radius of the conical vessel, r = 5 cm


Question. The internal and the external diameters of a hollow hemispherical vessel are 42 cm and 45.5 cm respectively. Find its capacity and outer curved surface area.
Solution. Let D = 45.5 cm be the external and d = 42 cm be the internal diameters of a hollow hemisphere.

Question. The sides of a right angled triangle are 15 cm and 8 cm. If the triangle is revolved around the hypotenuse, find the volume and curved surface area of the double cone generated.
Solution. Let ABC be the given triangle in which ∠ABC = 90°, AB = 15 cm, BC = 8 cm
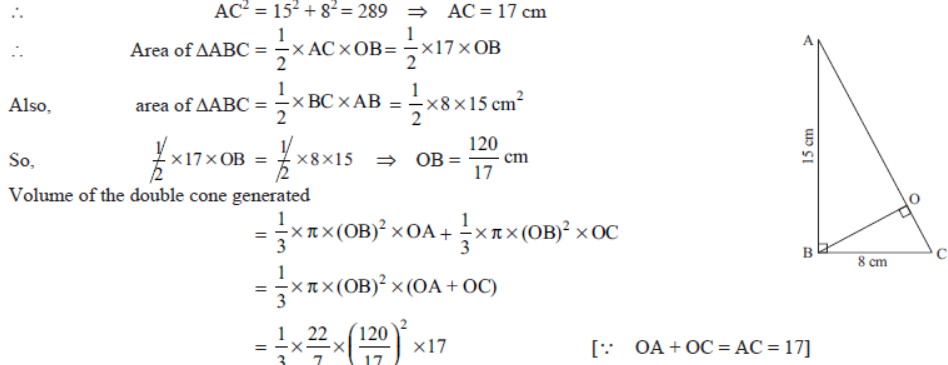
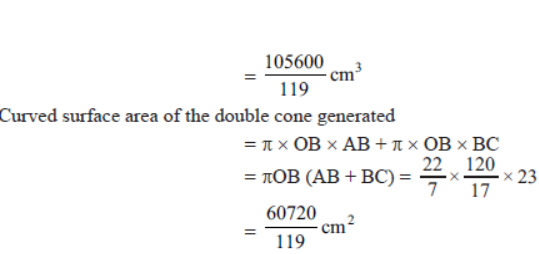

Question. A copper wire of diameter 8 mm is evenly wrapped on a cylinder of length 24 cm and diameter 49 cm to cover the whole surface. Find:
(i) the length of the wire (ii) the volume of the wire.
Solution. Given: The thickness of wire = its diameter = 8 mm = 0.8 cm.
And, the length of the cylinder = 24 cm
∴ Number of turns of the wire required to cover the whole surface of the cylinder

Question. How many coins of 1.75 cm in diameter and 2 mm thick must be melted to form a cuboid of 11 cm × 10 cm × 7 cm?
Solution. Let n coins to be melted.

Question. If the number of square centimetres on surface of a sphere is equal to the number of cubic centimetres in its volume, what is the diameter of the sphere?
Solution.

Question. A well is to be dug with 4 m inside diameter and 10 m in depth. Find the quantity of earth to be excavated.
The earth taken out is spread all round to a width of 4 m to form an embankment. Find the height of the embankment.
Solution. We have, inside radius (r) of the well = 4/2 m = 2 m

Question. Two cubes each of volume of 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Solution. Since, the volume of cube = (edge)3 ⇒ 64 = (Edge)3
⇒ (Edge)3 = 43
∴ Edge = 4 cm
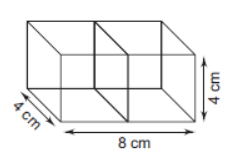
As two cubes are joined end to end, so for the resulting cuboid
length = 2 × 4 = 8 cm, breadth = 4 cm and height = 4 cm
So, required surface area = 2 [l × b + b × h + h × l]
= 2(32 + 16 + 32) = 160 cm2
Question. Two right circular cones X and Y are made. X having three times the radius of Y and Y having half the volume of the X. Calculate the ratio of the heights of X and Y.
Solution. Let radius (r1) of cone Y be r, then the radius (r2) of cone X = 3r
Let h1 and h2 be the heights of X and Y respectively.
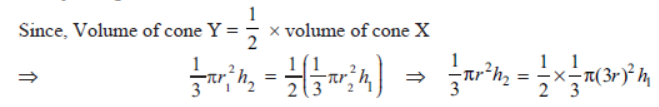

Short / Long Answer Types Questions :
Question. Two cones have their heights in the ratio 1 : 3 and radii in the ratio 3 : 1. What is the ratio of their volumes?
Solution. Let h1 and h2 be the heights of two cones.
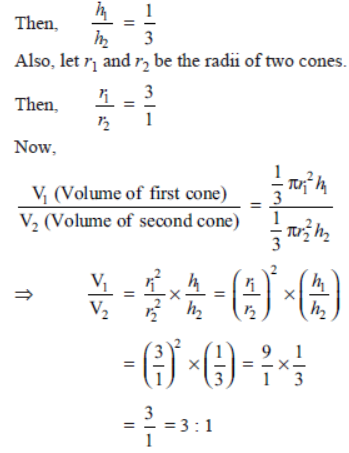
Question. Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.
Solution. 12 cm
Question. A cone and a cylinder have the same radii but the height of the cone is 3 times that of the cylinder. Find the ratio of their volumes.
Solution. Let the radii of a cone and a cylider be r
And, let the height of the cylinder be h
Then, the height of the cone = 3h
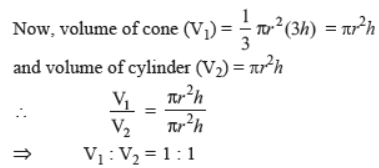
Question. In a rain-water harvesting system, the rain-water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3.5 m. If the tank is full, find the rainfall in cm.
Solution. Volume of rain water on the roof
= Volume of cylindrical tank
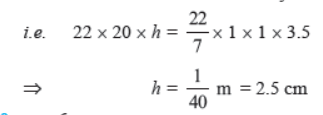
Question. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution. Radius of the sphere (r1) = 4.2 cm
∴ Volume of the sphere

Question. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution.

Thus, the required height of the platform is 2.5 m.
Question. In a hospital, used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park?
Solution. Volume of water in cylindrical tank
= Volume of water in park
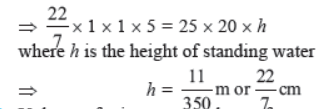
Question. Isha is 10 years old girl. On the result day, Isha and her father Suresh were very happy as she got first position in the class. While coming back to their home, Isha asked for a treat from her father as a reward for her success. They went to a juice shop and asked for two glasses of juice. Aisha, a juice seller, was serving juice to her customers in two types of glasses. Both the glasses had inner radius 3 cm. The height of both the glasses was 10 cm. Isha insisted to have the juice in first type of glass and her father decided to have the juice in second type of glass. Out of the two, Isha or her father Suresh, who got more quantity of juice to drink and by how much?

Solution. Capacity of first glass
Question. Three solid metal cubes of edges 6 cm, 8 cm and 10 cm are melted and recasted into a single solid cube. Find the length of the edge of the cube so obtained.
Solution. Volume of single cube so obtained
= (63 + 83 + 103) cm3
⇒ l3 = 216 + 512 + 1000 = 1728 ⇒ l = 12 cm
Question. A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution. Volume of rod = volume of wire

Question. A solid sphere is melted and recasted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm; find the radius of the sphere.
Solution. Volume of sphere = volume of hollow cylinder
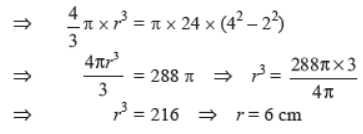
Question. The 3/4 th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
Solution. 3/4 x Volume of conical vessel
= Volume of cylindrical vessel (1)
Let the height of cylindrical vessel be h
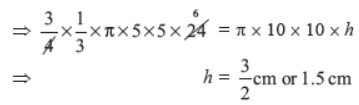
Question. Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Solution.
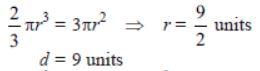
Question. A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere
Solution. Volume of sphere = volume of cone
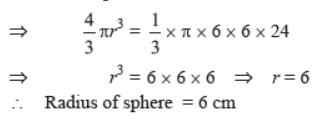
Question. The volume of a right circular cylinder with its height equal to the radius is 25,1/7 cm3. Find the height of the cylinder. [Use π = 22/7]
Solution. Let the height and radius of cylinder be r
[∴ Height of cylinder = radius of cylinder]
Then, Volume of cylinder = πr2h

Question. Find the radius of the sphere whose surface area is 36 p cm2.
Solution. Let r be the radius of sphere.
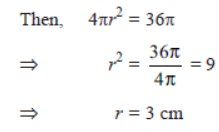
Question Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.
Solution.
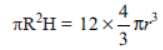
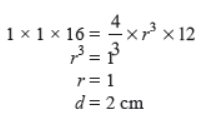
Question. Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted to form a solid sphere. Find the radius of the resulting sphere.
Solution. r1 = 6 cm
r2 = 8 cm
r3 = 10 cm
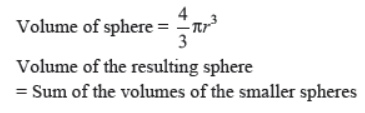

Question. In a cylindrical vessel of radius 10 cm, containing some water, 9000 small spherical balls are dropped which are completely immersed in water which raises the water level. If each spherical ball is of radius 0.5 cm, then find the rise in the level of water in the vessel.
Solution. Let radius of spherical ball, r1 = 0.5 cm
Then volume of one spherical ball,


Question. A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
Solution. Radius of conical heap = 12 m
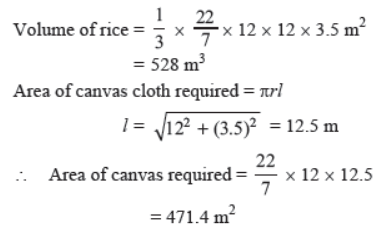
Question. If a solid right-circular cone of height 24 cm and base radius 6 cm is melted and recast in the shape of a sphere, find the radius of the sphere.
Solution. Volume of cone = volume of sphere

Question. A well, whose diameter is 3 m, has been dug 21 m deep and the earth dug out is used to form an embankment 4 m wide around it. Find the height of the embankment.
Solution. . 1.69 m
Question. Total surface area of a cube is 216 cm2. Find its volume.
Solution. 6l2 = 216 ⇒ l2 = 36
⇒ l = 6
∴ Volume of cube = l3 = (6)3 = 216 cm3
Question. Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm at the rate of 0.7 m/sec. By how much will the water rise in the tank in half an hour?
Solution. For pipe, r = 1 cm (½)
Length of water flowing in 1 sec,
h = 0.7 m = 70 cm (½)
Cylindrical Tank, R = 40 cm, rise in water level = H (½)
Volume of water flowing in 1 sec
= πr2h = π × 1 × 1 × 70 = 70p (½)
Volume of water flowing in 60 sec
= 70π × 60
Volume of water flowing in 30 minutes
= 70π × 60 × 30 (½)
Volume of water in Tank
= πr2H = π × 40 × 40 × H (½)
Volume of water in Tank
= Volume of water flowing in 30 minutes
π × 40 × 40 × H = 70π × 60 × 30 (½)
H = 78.75 cm
Question. A farmer connects a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution. Diameter of the pipe = 20 cm

Question. Total surface area of a cube is 216 cm2. Find its volume.
Solution. 6l2 = 216 ⇒ l2 = 36
⇒ l = 6
∴ Volume of cube = l3 = (6)3 = 216 cm3
Question. Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from an underground tank which is in the shape of a cuboid. The underground tank has dimensions 1.57 m × 1.44 m × 95 cm. The overhead tank has its radius of 60 cm and its height is 95 cm. Find the height of the water left in the underground tank after the overhead tank has been completely filled with water from the underground tank which had been full. Compare the capacity of the overhead tank with that of the underground tank. [Use π = 3.14]
Solution. The volume of water in the overhead tank equals the
volume of the water removed from the sump.
Now, the volume of water in the overhead tank (cylinder)
= pr2h = 3.14 × 0.6 × 0.6 × 0.95 m3
The volume of water in the sump when full
= l × b × h = 1.57 × 1.44 × 0.95 m3
The volume of water left in sump after filing tank
= [(1.57 × 1.44 × 0.95)
– (3.14 × 0.6 × 0.6 × 0.95)] m3
= (1.57 × 0.6 × 0.6 × 0.95 × 2) m2
So, the height of water left in the sump

Question. Find the curved surface area of a right-circular cone of height 15 cm and base diameter 16 cm.
Solution. Slant height of cone, l = √82 + 152 (∴ Diameter = 16 cm)
⇒ l = 17 cm
∴ CSA of cone = πrl = π × 8 × 17
= 136 π cm2
Question. How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Solution.
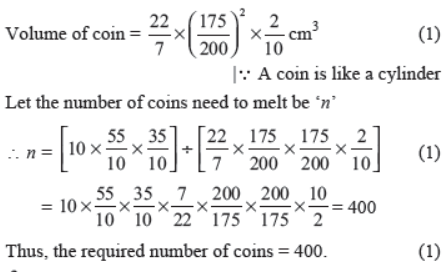
Question. Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm standing water is needed?
Solution. Let the area that can be irrigated in 30 minute be A m2 Water flowing in canal in 30 minutes

Assignments for Class 10 Mathematics Surface Area and Volume as per CBSE NCERT pattern
All students studying in Grade 10 Mathematics Surface Area and Volume should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Surface Area and Volume exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Surface Area and Volume which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.
Some advantages of Free Assignments for Class 10 Mathematics Surface Area and Volume
- Solving Assignments for Mathematics Surface Area and Volume Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
- By solving one assignment given in your class by Mathematics Surface Area and Volume teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
- You will be able to understand the type of questions which are expected in your Mathematics Surface Area and Volume class test
- You will be able to revise all topics given in the ebook for Class 10 Mathematics Surface Area and Volume as all questions have been provided in the question banks
- NCERT Class 10 Mathematics Surface Area and Volume Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
- Parents will be able to take print out of the assignments and give to their child easily.
All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Surface Area and Volume teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Surface Area and Volume Assignments PDF.

You can download free assignments for class 10 Mathematics Surface Area and Volume from https://www.assignmentsbag.com
You can get free PDF downloadable assignments for Grade 10 Mathematics Surface Area and Volume from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided assignments for all subjects in Grade 10, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge
Yes all test papers for Mathematics Surface Area and Volume Class 10 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.
https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.


