Assignments for Class 10 Mathematics Polynomials have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Polynomials from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Polynomials. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Polynomials book and get good marks in class 10 exams.
If (x ) is a polynomial in the highest power of (x)is called the degree of the polynomial (x).
- polynomial of degree 1 is called a linear polynomial . For example,4x-5 etc.
- A polynomial of degree 2 is called a quadratic polynomial. For example,x2+2x+3 etc.
- A polynomial of degree 3 is called a cubic polynomial and so on. For example, x3+2x2+x+5 etc.
Relationship between Zeroes and Coefficients of a Polynomial
- For Quadratic equation : If α and β are zeroes of the quadratic equation ax2 +bx +c,a≠0, then α + β =-b/a α β=c/a
- For cubic equation : If α, β and γ are zeroes of the cubic equation ax3 +bx2 +cx+d, a≠0 then α + β + γ =-b/a αβγ==d/aF.
Zero of a polynomial : if the value of p(x) at x=k is zero then K is called a zero of the polynomial p(x ).
Graphical representation of zero of a polynomial
- The zeroes of a polynomial p(x) are precisely the x-coordinates of the points, where the graph of y=p(x) intersects the x-axis.
- A quadratic polynomial can have at most 2 zeroes and a cubic polynomial can have at most 3 zeroes.
- For any quadratic polynomial ax2 +bx +c,a≠0 its graph gas one of the two shapes either open upwards or open downwards or open downwards depending on whether a>0 or a<0. F

Division Algorithm for Polynomials
If p(x) and g(x) are any two polynomials with g(x)≠0 then we can find
polynomials q(x) and r(x) such that p(x) =g(x) q(x) + r(x)
Where r(x) or degree of r(x) <degree of g(x).This result is known as the Division Algorithm for polynomials.
Question. Can x-2 be the remainder on division of a polynomial p(x) by x +3?
Sol. No, as degree (x -2) = degree (x +3)
Question. Find all the zeros of polynomial x4+x3-9x2-3x+18 if the two of its zeros are √3 and -√3.
Solution. Other Zeroes 2 and -3
Question. If α and β are the zeros of the quadratic polynomial x2 -6x +a find the value of ‘a’ If 3α +2β=20
Solution. a= -16
Question. If the number of apples and mangoes are the zeroes of polynomial 3x2-8x-2k+1. and the number of apples are 7 times the number of mangoes, then find the number of zeroes and value of k.
Solution. 2 zeroes, K= -2/3
Question. If α and β are the zeroes of a polynomial x2-x-30, then form a quadratic Polynomial whose zeroes are 2-α and 2- β
Solution. x2-3x-28
Question. On dividing 3x3-2x2+5x-5 by the polynomial p(x), the quotient and remainder are x2-x+2 and -7 respectively. Find p(x).
Solution. 3x-1
Question. Check whether x2 +3x +1 is a factor of 3x4+5x3 -7×2+2x+2?
Solution. x2-2√3x+2
Question. If α and β are the zeros of quadratic polynomial p(x) =x2-(k-6) x+ (2k+1) Find the value of k if α+β=αβ.
Solution. K= -7
Question. If one zero of the quadratic polynomial f(x) =4x2-8kx-9 is negative of the other, find the value of k.
Solution. k= 0
Question. On dividing 3x3+4x2+5x-13by a polynomial g(x) ,the quotient and remainder are 3x+10and 16x-43 respectively. Find the polynomial g(x).
Solution. g(x) =x2-2x+3
Question. Find the value of k for which the quadratic polynomial 9x2-3kx+k has equal zeros.
Solution. k= 0 or k=4
Question. If the zeros of polynomial x2-5x+k are the reciprocal of the zeros then find the value of k.
Solution. K=1
Question. If the sum of squares of zeros of the polynomial 6x2+x+k is 25/36 find the value of k.
Solution. K= -7
Question. Find a cubic polynomial with the sum of the zeroes, sum of the products of its zeroes taken two at a time, and the product of its zeroes as 2, – 7, -14 respectively.
Sol. Let the cubic polynomial be p(x) = ax3 + bx2 + cx + d. Then

Question. If the graph of a polynomial intersects the x-axis at only one point, it cannot be a quadratic polynomial.
Sol. False, because every quadratic polynomial has at most two zeroes.
Question. Can a quadratic polynomial x2 + kx + k have equal zeroes for some odd integer k >1?
Sol. No, for equal zeroes, k = 0,4
⇒ k is even
Are the following statements ‘True’ or ‘False’? Justify your answer.
Question. If a and b are the zeroes of the quadratic polynomial f (x) = 2x2 – 5x + 7, find a polynomial whose zeroes are 2a + 3b and 3a + 2b.
Sol. Since a and b are the ze roes of the quad ratic poly no mial f (x) = 2x2 – 5x + 7.
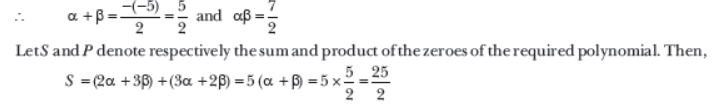

Question. If the zeroes of a quadratic polynomial ax2 + bx + c are both negative, then a, b and c all have the same sign.
Sol. True, because – b/a
= sum of zeroes < 0, so that b/a > 0. Also the product of the zeroes = c/a > 0.
Question. Find the zeroes of the polynomial f (x) = x 3 – 5x2 – 2x + 24, if it is given that the product of its two zeroes is 12.
Sol. Let a, b and g be the zer oes of polyn om ial f (x) such that ab =12.


Question. What will the quotient and remainder be on division of ax2 + bx + cby px3 + qx2 + rx +5, p ≠ 0?
Sol. 0, ax2 + bx + c
1. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) x2 + 3x +1, 3x4 + 5x3 – 7x2 + 2x + 2 (ii) t2 – 3, 2t4 + 3t3 – 2t2 – 9t -12
Sol.

Question. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) 6x2 – 3 – 7x (ii) 4u2 + 8u (iii) 4s2 – 4s +1
Sol. (i) We have,
p (x) = 6x2 – 3 – 7x
⇒ p (x) = 6x2 – 7x – 3 (In general form)
= 6x2 – 9x + 2x – 3
= 3x (2x – 3) +1 (2x – 3) = (2x – 3) (3x +1)
The zeroes of polynomial p (x) is given by
p (x) = 0
⇒ (2x – 3) (3x +1) = 0 ⇒ x = 3/2 -1/3,
Thus, the zeroes of 6x2 – 7x – 3 are α = 3/2 and β = – 1/3

Therefore, product of zeroes = Constant term/Coefficient of x2
(ii) We have,
p (u) = 4u2 + 8u ⇒ p(u) = 4u (u + 2)
The zeroes of polynomial p (u) is given by
p (u) = 0 ⇒ 4u (u + 2) = 0
∴ u = 0, – 2
Thus, the zeroes of 4u2 + 8u are a = 0 and b = – 2
Now, sum of the zeroes = a + b = 0 – 2 = – 2
and (Coefficient of u )/ Coefficient of u 2=-8/4= -2
Therefore, sum of the zeroes = -(Coefficient of u) /(Coefficient of u2)
Again, product of the zeroes = αβ = 0 x (- 2) = 0 and Constant term/Coefficient of u2 =0/4=0
Therefore, product of zeroes = Constant term/Coefficient of u2
(iii) We have,
p (s) = 4s2 – 4s +1
⇒ p (s) = 4s2 – 2s – 2s +1 = 2s (2s -1) -1 (2s -1) = (2s -1) (2s -1)
The zeroes of polynomial p (s) is given by
p (s) = 0
⇒ (2s -1) (2s -1) = 0
⇒ s = 1/2-1/2,
Thus, the zeroes of 4s2 – 4s +1 are

and Constant term/Coefficient of s 2 = 1/4
∴ Product of zeroes = Constant term/Coefficient of s 2
Question. If the graph of a polynomial intersects the x-axis at exactly two points, it need not be a quadratic polynomial.
Sol. True, x4 -1 is a polynomial intersecting the x-axis at exactly two points
Question. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) – 1/4 , 1/4 (ii) √2,1/3
Sol.

Question. Verify that the numbers given alongside the cubic polynomial below are their zeroes. Also verify the relationship between the zeroes and the coefficients.
x3 – 4x 2 + 5x – 2; 2,1,1
Sol. Let p(x) = x3 – 4x2 + 5x – 2
On comparing with general polynomial p(x) = ax3 + bx2 + cx + d, we get a =1, b = – 4 , c = 5 and d = – 2.
Given zeroes 2, 1, 1.
∴ p(2) = (2)3 – 4(2)2 + 5(2) – 2 = 8 -16 +10 – 2 = 0
and p (1) = (1)3 – 4 (1)2 + 5(1) – 2 =1 – 4 + 5 – 2 = 0.
Hence, 2,1 and 1 are the zeroes of the given cubic polynomial.
Again, consider a = 2, b =1, g =1
∴ α + β + γ = 2 +1 +1 = 4
Question. Determine the degree of the polynomial (x + 1) (x2 – x – x4 + 1).
Solution. Given polynomial in standard form is :
–x5 – x4 + x3 + 1
So, its degree is 5
Question. If the product of two zeros of the polynomial
p(x) = 2x3 + 6x2 – 4x + 9 is 3, find the third zero of the polynomial.
Solution. If α, β, and γ be the three zeros of p(x). Then,
αβγ = – 9/ 2
Since, αβ = 3,
we get γ = − × = − 9/ 2 × 1/3 = -3/2
Thus, the third zero of p(x) is − 3/ 2
Question. Find the zeroes of following polynomials by factorisation method and verify relation between the zeroes and coeffcients of polynomials.
(A) 2x2 + 2/ 7 x + 4 3
(B) 2s2 − (1 + 2 √2)s + √2
(C) 7y2 – 11/3 y – 3/ 2
Solution. (A) Let f(x) = 2x2 + 7/2 x + 3/4 = 8x2 + 14x + 3
(Multiplying the given equation by 4)
= 8x2 + (12x + 2x) + 3
= 8x2 + 12x + 2x + 3
= 4x(2x + 3) + 1(2x + 3)
= (2x + 3)(4x + 1)
The zeroes of f(x) are given by f(x) = 0.
So, the value of 2x2 + 7/2 x + 3/4 is zero when
x = – 3/2 or x = –1/ 4
⇒ x = – 3/2 , – 1/4
Question. If a and b are the zeros of the polynomial p(x) = 4x2 – 2x – 3, find the value of 1/α + 1/β .
Solution. Here, α+ β = 2/ 4 or 1/ 2 and α.β = −3/ 4 .
So, 1/α + 1/β = α + β /αβ = 1/2/-3/4 =-2/3
Question. If one of the zeros of polynomial p(x) =
(k − 1)x2 – kx + 1 is −3, find the value of k.
Solution. Since, (–3) is a zero of p(x), we have,
(k – 1)(–3)2–k(–3) + 1 = 0
⇒ 9k–9 + 3k + 1 = 0,
⇒ 12k = 8 ⇒ k = 2/ 3
Question. If α and β be the roots of the equation x2 − 1 = 0 , then show that: α + β = 1/α + 1/β
Solution. Here, α + β = 0/ 1 = 0
[∵ Sum of roots = Coefficient of x / Coefficient of x2 ]
Also, 1/α + 1/β = α + β /αβ = 0/1 = 0
Thus, α + β = 1/α + 1/β
Question. A teacher asked 10 of his students to write a polynomial in one variable on a paper and then to handover the paper. The following were the answer given by the students:
2x + 3, 3x2 + 7x + 2, 4x3 + 3x2 + 2, x3 + √3x + 7, 7x + √7 , 5x3 – 7x + 2, 2x3 + 3 – 5 x , 5x – 1/2 , ax3 + bx2 + cx + d, x + 1 x .
Answer the following Questions:
(A) How many of the above ten are not polynomials?
(B) How many of the above ten are quadratic polynomials?
Solution. (A) Three, namely: x3 + √3x + 7 , 2×2 + 3 − 5/x , x+1/x
(As they contain square roots of the variable and negative power of x)
(B) One, namely 3×2 + 7x + 2
Question. If one of the zeroes of the quadratic polynomial f(x) = 4x2 – 8kx – 9 is equal in magnitude but opposite in sign of the other, then find the value of k.
Solution. f(x) = 4x2 – 8kx – 9
Let one of the zeroes of the polynomial be
and the other zeroes be – α
Sum of zeroes = (− b /a) = 8k/4
α + (- α) = 0
So, 8k/ 4 = 0 ⇒ k = 0
Question. Can (x – 5) be the remainder on division of a polynomial p(x) by (x + 8)?
Solution. No. We know that we cannot divide the polynomials which have same degree.
As we can see that degree of (x – 5) = degree of (x + 8)
So, they are not divisible.
Question. If the zeros of the polynomial x3 – 2x2 + x + 1 are a – b, a and a + b, then find the values of a and b.
Solution. As (a – b), a and (a + b) are zeros of x3 – 3x2 + x + 1, we have:
a – b + a + a + b = 3
⇒ 3a = 3, or a = 1 …(i)
a (a – b) + a (a + b) + (a – b) (a + b) = 1
⇒ 3a2 – b2 = 1 …(ii)
and (a – b) a (a + b) = –1
⇒ a(a2 – b2) = –1 …(iii)
From (i) and (ii), we have b = ± √2
Thus, a = 1, b = ± √2
Question. Form a quadratic polynomial, the sum and product of whose zeroes are (–3) and 2 respectively.
Solution. A general form of a quadratic polynomial is
ax2 + bx + c
Here, α + β = − b/ a = – 3 and a.b = − b/ a = 2
where, a and b are the roots of given polynomial.
So, the required polynomial is x2 + 3x + 2.
Question. Find the value of k for which the roots of the equation 3x2 − 10x + k = 0 are reciprocal of each other.
Solution. Given, equation is 3×2 – 10x + k = 0, where roots are reciprocals of each other.
Let the roots be α and 1/ α
∴ Product of roots = c/ a
⇒ α . 1/α = k /3 [∵ a = 3, b = – 10, c = k]
⇒ 1 = k /3
⇒ k = 3
Question. What number should be added to the polynomial x2 – 5x + 4 so that 3 is the zero of the polynomial?
Solution. Let k be the number to be added to the given polynomial.. Then the polynomial becomes x2 – 5x + (4 + k)
As 3 is the zero of the polynomial, we get:
(3)2 – 5(3) + (4 + k) = 0
⇒ (4 + k) = 15 – 9
⇒ 4 + k = 6
⇒ k = 2
Thus, 2 is to be added to the polynomial
Question. If the zeroes of a polynomial x2 – 8x + k = 0, is the HCF of (6, 12), then find the value of k.
Solution. HCF of (6, 12) = 6
So, 6 is one of the roots of the polynomial.
f(x) = x2 – 8x + k = 0
f(6) = (6)2 – 8(6) + k = 0
36 – 48 + k = 0
–12 + k = 0 ⇒ k = 12.
Question. Find a quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial f(x) = ax2+ bx + c, a ≠0 , c ≠ 0.
Solution. Let α, β be the zeroes of f(x) = ax2 + bx + c. Thus
α + β = – b/ a and αβ = c/a
Now, 1/α + 1/β = α + β / αβ = -b/a/c/a = – b/c
1/α . 1/β = 1/αβ = 1/c/a = a/c
∴ Polynomial is: x2 – (sum of roots) x
– product roots
x2 – (-b/c)x + a/c = 0
⇒ cx2 + bx + a = 0
So, the required polynomial is cx2 + bx + a.
Question. If the zeroes of the polynomial x2 + px + q are double the value to the zeroes of 2x2 – 5x − 3, find the value of p and q.
Solution. Let α and β are zeroes of the 2x2 – 5x – 3
α + β = – b/a = 5/2
αβ = c/a =− 3/2
According to the question,
2α and 2β are zeroes of x2 + px + q
2α + 2β = –p ⇒ 2(α + β) = –p
2 x (5/2) = -p
= –p [from eqn. (i)]
p = –5
2α × 2β = q ⇒ 4αβ = q
4 x(- 3/2) q = –6
Hence, p = –5 and q = –6.
Question. Find the value of k such that the polynomial x2 – (k + 6)x + 2(2k 1) has the sum of its zeros equal to half of their product.
Solution. Given polynomial is :
p(x) = x2 – (k + 6) x + 2(2k – 1)
In the given quadratic equation:
a = 1
b = – (k + 6)
c = 2(2k – 1)
Sum of zeroes = – b/ a
= k + 6 …(i)
Product of zeroes = c/a
= 2(2k – 1) …(ii)
According to the given condition:
Sum of the zeroes = 1 /2 × Product of zeroes
⇒ k + 6 = 1/ 2
× 2 (2k – 1)
⇒ k + 6 = 2k – 1
⇒ 2k – k = 6 + 1
⇒ k = 7
Hence, the value of k is 7.
Question. Find the quadratic polynomial sum and product of whose Zeroes are – 1 and – 20 espectively. also, find the zeroes of the polynomial so obtained.
Solution. Let α and β the zeroes of the polynomial.
Given : sum of zeroes, α + β = – 1
product of zeroes, αβ = – 20
Equation of polynomial :
x2 – (sum of zeroes) x + product of zeroes = 0
∴ x2 – (– 1)x + (– 20) = 0
⇒ x2 + x – 20 = 0
On spliting the middle term,
x2 + 5x – 4x – 20 = 0
⇒ x(x + 5) – 4(x + 5) = 0
⇒ (x – 4) (x + 5) = 0
⇒ x = 4, – 5
Hence, the zeroes of the polynomial are 4 and –5.
Question. Given that 2 is a zero of the cubic polynomial 6x3 + √2 x2 + 10x – 4√ 2 , find its other two zeroes.
Solution. Let p(x) = 6x3 + √2x2 – 10x – 4 √2 As 2 is one of the zeroes of p(x).
⇒ g(x) = (x – √2) is one of the factors of p(x).

Question. Given that x – 5 is a factor of the cubic polynomial x3 – 3 √5 x + 13x – 3 √5 , find all the zeroes of the polynomial.
Solution. Let p(x) = x3 – 3 √5 x2 + 13x – 3 √5 As 5 is one of the zeroes of p(x).
⇒ (x – 5 ) is one of the factors of p(x).
x2 – 2 5 x + 3

Question. If one root of the equation 3x2 – 8x + 2k + 1 = 0 is seven times the other, find the two roots and the value of k.
Solution. Let α and 7α be the two roots of the equation:
3x2 – 8x + (2k + 1) = 0
Then, α + 7α = 8α = 8 /3 …..(i)
and α.(7α) = 7α2 = 2k + 1/3 …..(ii)
From (i) α = 1/ 3 . So, the two roots are 1/ 3 and 7/ 3
Using α = 1 3 in (ii), we have:
7( 1/3)2 =2k + 1/3
⇒ 2k + 1 = 7/3
⇒ 2k = 4/3
⇒ k = 2/3
Question. Given that the zeroes of the cubic polynomial x3 – 6x2 + 3x + 10 are of the form a, a + b, a + 2b for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.
Solution. Let p(x) = x3 – 6x2 + 3x + 10


Question. Find a quadratic polynomial whose zeroes are 1 and -3. Verify the relation between the coefficients and Zeroes of polynomial.
Solution. Sum of zeroes, S = 1 + (–3) = –2 …(i)
Product of zeroes, P = 1 × (–3) = –3 …(ii)
Quadratic polynomial
p(x) = x2 – Sx + P
= x2 – (–2)x – 3 = x2 + 2x – 3
Here, a = 1, b = 2, c = –3
− b/ a = −2 /1 =- 2
Sum of zeroes = − b/ a = 2 [using eqn. (i)]
Also, c/a = -3/1 = -3
Product of zeroes = c/a = -3 [using eqn. (ii)]
Question. For which values of a and b are the zeroes of q(x) = x3 + 2x2 + a also the zeroes of the polynomial p(x) = x5 – x4 – 4x3 + 3x2 + 3x + b?
Solution. Let p(x) = x5 – x4 – 4x3 + 3x2 + 3x + b and q(x) = x3 + 2x2 + a.
Since, the zeroes of the polynomial q(x) are also zeroes of p(x), we can say that q(x) is a factor of p(x).
Then, on dividing

Question. Without actually calculating the zeroes, form a quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial 5x2 + 2x – 3.
Solution. Let α and β be the zeroes of 5x2 + 2x – 3

Question. Obtain other zeroes of the polynomial f(x) = 2x4 + 3x3 – 5x2 – 9x – 3 if two of its zeroes are −√3 and − √3
Solution. Since √3 and − √3 are zeroes of f(x), (x − √3)(x + √3) i.e., (x2 – √3) is a factor of f(x) to obtain other two zeroes, we shall determine the quotient, by dividing f(x) with (x2 – √3)
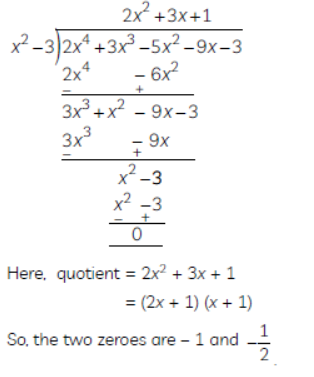
Question Find the zeroes of the following polynomials and verify the relationship between the zeroes and the coefficients of the polynomials.
(i) 3x2 + 4x – 4
(ii) 7y2 -(11/3) y – 2/3
(iii) 4x2 +5√2x -3
(iv) p2 -30
(v) √3x2 -11x +6√3
(vi) a(x2 +1) – x(a2 +1)
(vii) 6x2 + x -2
(viii) y2 -1/2 y + 1/16
Answer
(i) – 2, 2/3
(ii) -1/7 , 2/3
(iii) -3√2/2 , 2/4
(iv) √30 ,– √30
(v) 2/√3 , 3√3
(vi) a , 1/a
(vii) -2/3 , 1/2
(viii) 1/4 , 1/4
10. If the sum of the zeroes of the quadratic polynomial f(x) = kx2 +2x +3k is equal to their product, find the value of k.
Answer
k = -2/3
Question. (i) Obtain all other zeroes of 2x4 +7x3 -19x2 -14x +30, if two of its zeroes are 2 and – 2.
(ii) Obtain all other zeroes of 2x3 + x2 -6x -3, if two of its zeroes are – 3 and 3.
Answer
(i) – 5, 3/2
(ii) -1/2
Question. Find a quadratic polynomial each with the given numbers as the sum and product of the zeroes respectively.
(iv) 21/8 , 5/16
Also find the zeroes of those polynomials by factorisation.
Answer
(iv) 1/16 (16x2 – 42x +5); (1/8) , (5/2)
Question. Check whether g(x) is a factor of p(x) by dividing the first polynomial by the second polynomial:
(i) p(x) = 4x3 +8x +8x2 +7, g(x) = 2x2 – x +1
(ii) p(x) = x4 -5x +6, g(x) = 2 – x2
(iii) p(x) =13x3 -19x2 +12x +14, g(x) = 2 -2x + x2
Answer
(i) No
(ii) No
(iii) Yes
Question. If (x -2) is a factor of x 3 + ax 2 + bx +16 and b = 4a, find the values of a and b.
Answer
a = – 2,
b = – 8
Question. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = 0
(iii) deg r(x) = 0
Answer
(i) 2x2 -3= 2(x2 +1) -5
(ii) x3 +1= 0.(x4 ) +(x3 +1)
(iii) x2 +1=1(x2 -1) +2
Question. If a and b are the zeroes of the quadratic polynomial f(x) = 3x2 -5x -2, then evaluate
(i) α2 +β2 (ii) α3 +β3 (iii) α2/β+β2/α
Answer
(i) 37/9
(ii) 215/27
(iii) -215/18
Question. Find the cubic polynomial with the sum, sum of the products of its zeroes taken two at a time, and the products of its zeroes as –3, –8 and 2 respectively.
Answer
x3 +3x2 -8x -2
Question. A cubic polynomial always has degree three.
Answer
Yes, 4x3 +3x2 +2x +1 is a cubic polynomial
Question. The degree of a binomial cannot be more than two.
Answer
False, x3 +1 is a binomial of degree 3
Question. We can have a trinomial having degree 7.
Answer
Yes, x7 + x -1.
Question. There is only one term of degree one in a monomial.
Answer
False, 4x2 is a monomial of degree 2
Assignments for Class 10 Mathematics Polynomials as per CBSE NCERT pattern
All students studying in Grade 10 Mathematics Polynomials should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Polynomials exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Polynomials which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.
Some advantages of Free Assignments for Class 10 Mathematics Polynomials
- Solving Assignments for Mathematics Polynomials Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
- By solving one assignments given in your class by Mathematics Polynomials teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
- You will be able to understand the type of questions which are expected in your Mathematics Polynomials class test
- You will be able to revise all topics given in the ebook for Class 10 Mathematics Polynomials as all questions have been provided in the question banks
- NCERT Class 10 Mathematics Polynomials Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
- Parents will be able to take print out of the assignments and give to their child easily.
All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Polynomials teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Polynomials Assignments PDF.

You can download free assignments for class 10 Mathematics Polynomials from https://www.assignmentsbag.com
You can get free PDF downloadable assignments for Grade 10 Mathematics Polynomials from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided assignments for all subjects in Grade 10, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge
Yes all test papers for Mathematics Polynomials Class 10 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.
https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.
