Please refer to Assignments Class 9 Mathematics Triangles Chapter 7 with solved questions and answers. We have provided Class 9 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 7 Triangles Class 9 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Triangles Assignments Class 9 Mathematics
Solved Examples
Example : Observe the following figure.
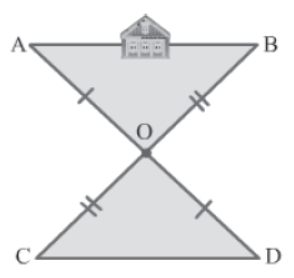
Ajay wishes to determine the distance between two objects A and B, but there is a house in between. So, he devises an ingenious way to fix the problem. First, he fixes a pole at any point O so that both A and B are visible from O. He then fixes another pole at point D which is collinear to point O and object A, and is at the same distance from O as A, i.e., DO = AO.
Similarly, he fixes a pole at point C which is collinear to point O and object B, and is at the same distance from O as B, i.e., CO = BO. Finally, he measures CD to find the distance between A and B. How can Ajay be sure that CD = AB?
Solution:
We have two triangles in the given figure, i.e., ΔAOB and ΔDOC.
In these two triangles, we have:
AO = DO (Given)
∠AOB = ∠DOC (Vertically opposite angles)
BO = CO (Given)
Therefore, by the SAS congruence rule, we can say that:
ΔAOB ≅ ΔDOC
⇒ AB = CD (By CPCT)
This is the reason why Ajay measures CD to find the distance between objects A and B.
Example 2: In the given quadrilateral PQRS, PR bisects ∠QPS and PQ = PS. Prove that:
i) ΔPQR ≅ΔPSR
ii) QR = SR
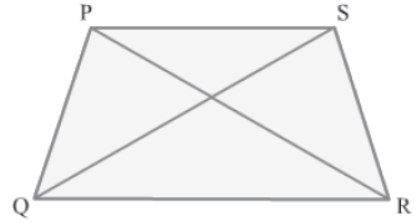
Solution:
i) In ΔPQR and ΔPSR, we have:
PQ = PS(Given)
PR = PR(Common side)
∠QPR = ∠SPR(&because PR bisects ∠QPS)
So, by the SAS congruence rule, we obtain:
ΔPQR ≅ ΔPSR
ii) We have proved that ΔPQR ≅ ΔPSR.
∴ QR = SR (&because Corresponding parts of congruent triangles are equal)
Example 1: In the shown figure, PR = QS and ∠QPR = ∠PQS. Prove that ΔPQR ≅ ΔQPS. Also, show that PS = QR and ∠QPS = ∠PQR.
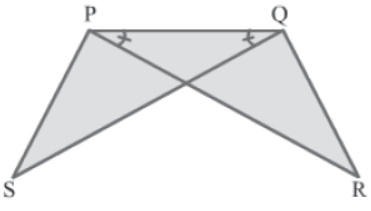
Solution:
In ΔPQR and ΔQPS, we have:
PR = QS(Given)
∠QPR = ∠PQS(Given)
PQ = PQ(Common side)
∴ ΔPQR ≅ ΔQPS(By the SAS congruence criterion)
⇒ PS = QR and ∠QPS = ∠PQR (By CPCT)
Example 2: Prove that ΔPQR is isosceles if the altitude drawn from a vertex bisects the opposite side.
Solution:
The given figure shows the ΔPQR having PS as an altitude that bisects the opposite side QR.
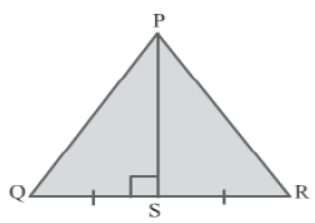
In ΔPSQ and ΔPSR, we have:
QS = SR (&because Altitude PS bisects QR)
PS = PS(Common side)
∠PSQ = ∠PSR = 90°(&because PS is the altitude to QR)
∴ ΔPSQ ≅ ΔPSR(By the SAS congruence rule)
⇒ PQ = PR(By CPCT)
Therefore, ΔPQR is isosceles.
Example 3: If the angle bisector of any angle of a triangle bisects the opposite side then show that the triangle is isosceles.
Solution:
Let ΔPQR be the given triangle and PS is the angle bisector of ∠QPR such that it bisects the side QR.
Let us extend the segment PS to point T such that PS = TS.
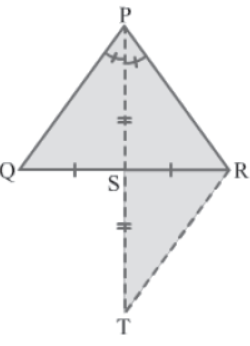
In ΔPQS and ΔTRS, we have
QS = RS (Given)
∠PSQ = ∠TSR (Vertically opposite angles)
PS = TS (By construction)
So, by the SAS congruence criterion, we have:
ΔPQS ≅ ΔTRS
By CPCT, we obtain
PQ = TR …(1)
And ∠QPS = ∠RTS …(2)
But ∠QPS = ∠RPS …(3) (PS bisects ∠QPR)
∴ ∠RTS = ∠RPS [From (2) and (3)]
⇒ PR = TR (Sides opposite to equal angles)
∴ PQ = PR [From (1)]
Thus, ΔPQR is an isosceles triangle.
Example 1: ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA.
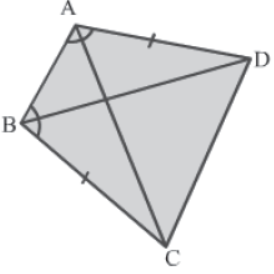
Prove that:
i) ΔABD ≅ ΔBAC
ii) BD = AC
iii) ∠ABD = ∠BAC
Solution:
i) In ΔABD and ΔBAC, we have:
AD = BC (Given)
∠DAB = ∠CBA (Given)
AB = BA (Common side)
So, by the SAS congruence criterion, we have:
ΔABD ≅ ΔBAC
ii) We have proved that ΔABD ≅ ΔBAC.
∴ BD = AC (By CPCT)
iii) Since ΔABD ≅ ΔBAC, we have:
∠ABD = ∠BAC(By CPCT)
Example 2: In the given figure, PR = PO, PQ = PS and ∠QPS = ∠OPR. Show that QR = SO.
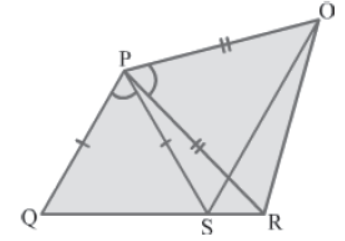
Solution:
It is given that ∠QPS = ∠OPR.
∴ ∠QPS + ∠SPR = ∠OPR + ∠SPR
⇒ ∠QPR = ∠SPO… (1)
In ΔQPR and ΔSPO, we have:
PQ = PS (Given)
∠QPR = ∠SPO (From equation 1)
PR = PO (Given)
So, by the SAS congruence rule, we have:
ΔQPR ≅ ΔSPO
⇒ QR = SO (By CPCT)
Example 3: In an isosceles triangle, prove that the medians on the equal sides are equal.
Solution:
Let ΔPQR be an isosceles triangle such that PQ = PR.
Also, let RS and QT be the medians to the sides PQ and PR respectively.

In ΔPQR, we have
PS = SQ = 1/2 PQ (RS is the median)
And PT = TR = 1/2 PR (QT is the median)
But PQ = PR
∴ PS = SQ = PT = TR …(1)
In ΔPRS and ΔPQT, we have
PQ = PR (Given)
∠RPS = ∠QPT (Common angle)
PS = PT [From (1)]
So, by the SAS congruence rule, we have:
ΔPRS ≅ ΔPQT
∴ RS = QT (By CPCT)
Thus, the medians on the equal sides of an isosceles triangle are equal.
Proving Theorem of Right Angled Triangle
There is a theorem of right angled triangles which states that:
Example 1: Check whether the given triangles are congruent or not.
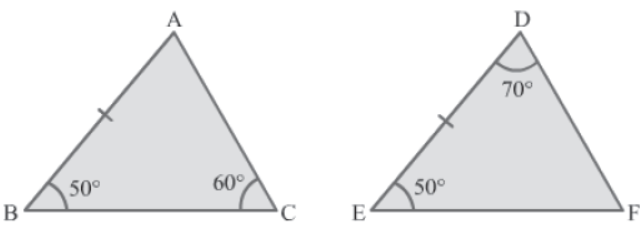
Solution:
In ΔABC, we have:
∠ABC + ∠BCA + ∠BAC = 180° (By the angle sum property)
⇒ 50° + 60° + ∠BAC = 180°
⇒ 110° + ∠BAC = 180°
⇒ ∠BAC = 180° − 110°
⇒ ∠BAC = 70°
In ΔABC and ΔDEF, we have:
∠BAC = ∠EDF = 70°
AB = DE (Given)
∠ABC = ∠DEF = 50°
Therefore, by the ASA congruence rule, we have:
ΔABC ≅ ΔDEF
Example 2: In the given figure, AB and CD are two equal and parallel lines. Prove that ΔABO ≅ ΔCDO.
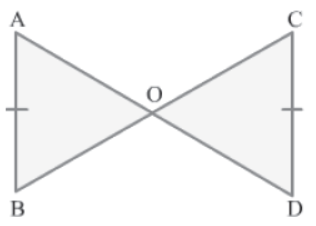
Solution:
It is given that AB||CD. AD and BC are transversals lying on lines AB and CD.
So, by the alternate angles axiom, we obtain:
∠OAB = ∠ODC… (1)
∠OBA = ∠OCD… (2)
In ΔABO and ΔCDO, we have:
∠OAB = ∠ODC (By equation 1)
AB = CD(Given)
∠OBA = ∠OCD (By equation 2)
Thus, by the ASA congruence rule, we obtain:
ΔABO ≅ ΔCDO
Example 1: In the given quadrilateral ABCD, diagonal AC bisects ∠BAD and ∠BCD. Prove that AB = AD and CB = CD.
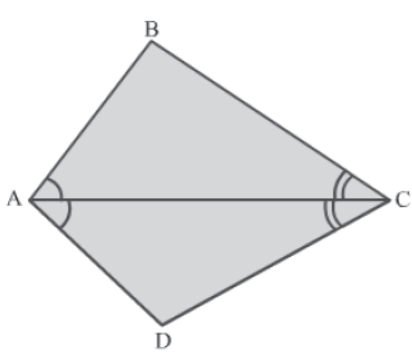
Solution:
Since diagonal AC bisects ∠BAD and ∠CAD, we have:
∠BAC = ∠DAC and ∠BCA = ∠DCA
In ΔACB and ΔACD, we have:
∠BAC = ∠DAC (Given)
∠BCA = ∠DCA (Given)
AC = AC (Common side)
So, by the ASA congruence rule, we have:
ΔACB ≅ ΔACD
⇒ AB = AD and CB = CD (By CPCT)
Example 2: Consider the two triangular parks ABC and DEF shown below.
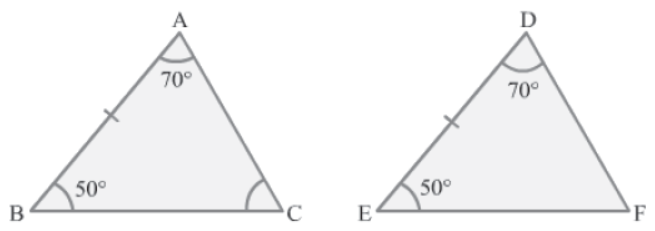
Tina jogs around park ABC and Aliya jogs around park DEF daily. Paths AB and DE are equal in length. If both girls jog an equal number of rounds daily, then check whether or not they cover the same distance while jogging?
Solution:
In ΔABC and ΔDEF, we have:
∠BAC = ∠EDF = 70°(Given)
AB = DE(Given)
∠ABC = ∠DEF = 50°(Given)
Therefore, by the ASA congruency rule, we obtain:
ΔABC ≅ ΔDEF
⇒ AC = DF and BC = EF(By CPCT)
∴ AB + BC + CA = DE + EF + FD
Hence, both Tina and Aliya cover the same distance daily while jogging.
Example 1: The given ΔABC is isosceles with AB = AC. ∠LOC = 2∠OBC and ∠MOB = 2∠OCB.
Prove that ΔBCM ≅ ΔCBL.
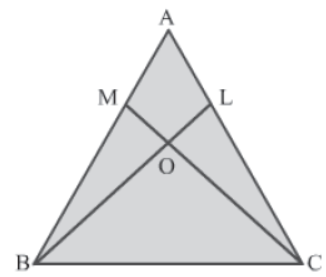
Solution:
It is given that:
∠LOC = 2∠OBC… (1)
∠MOB = 2∠OCB… (2)
Now, ∠LOC = ∠MOB (Vertically opposite angles)
Using equations (1) and (2), we obtain:
∠OCB = ∠OBC
⇒ ∠MCB = ∠LBC… (3)
In ΔBCM and ΔCBL, we have:
∠MBC = ∠LCB (∵ ΔABC is isosceles with AB = AC)
BC = CB (Common side)
∠MCB = ∠LBC (Using equation 3)
Thus, by the ASA congruence rule, we obtain:
ΔBCM ≅ ΔCBL
Example 2: In the given figure, ∠BCD = ∠ADC and ∠ACB = ∠BDA. Prove that AD = BC and ∠CAD = ∠DBC.
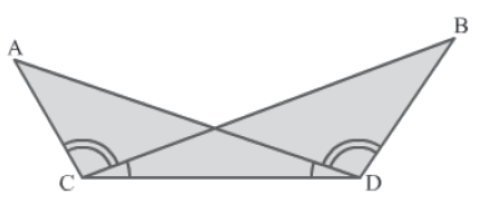
Solution:
It is given that:
∠BCD = ∠ADC … (1)
∠ACB = ∠BDA … (2)
On adding equations (1) and (2), we get:
∠BCD + ∠ACB = ∠ADC + ∠BDA
⇒ ∠ACD = ∠BDC… (3)
In ΔACD and ΔBDC, we have:
∠ADC = ∠BCD(Given)
CD = DC (Common side)
∠ACD = ∠BDC (By equation 3)
So, by the ASA congruence rule, we have:
ΔACD ≅ ΔBDC
⇒ AD = BC and ∠CAD = ∠DBC (By CPCT)
AAS Congruence Rule
Example 1: The given ΔABC is isosceles with AB = AC and ∠ADC = ∠AEB. Prove that ΔABE ≅ ΔACD.
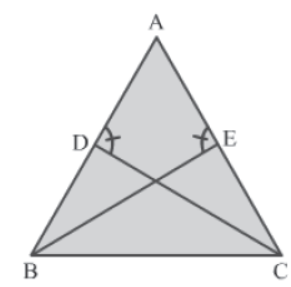
Solution:
In ΔABE and ΔACD, we have:
AB = AC (Given)
∠AEB = ∠ADC (Given)
∠BAE = ∠CAD (Common angle)
Thus, by the AAS congruence rule, we obtain:
ΔABE ≅ ΔACD
Example 2: In the given figure, OR bisects ∠POQ and A is any point on OR. AB and AC are the perpendiculars drawn from A to the arms OP and OQ respectively. Prove that ΔAOB ≅ ΔAOC.
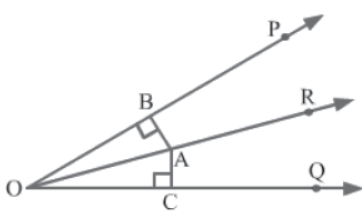
Solution:
It is given that OR bisects ∠POQ.
∴ ∠POR = ∠QOR
⇒ ∠BOA = ∠COA… (1)
In ΔAOB and ΔAOC, we have:
∠ABO = ∠ACO = 90° (∵ AB and AC are perpendiculars)
∠BOA = ∠COA (By equation 1)
AO = AO (Common side)
Thus, by the AAS congruence rule, we obtain:
ΔAOB ≅ ΔAOC
Example 1: If two angles of a triangle are equal, then prove that the sides opposite them are also equal.
Solution:
Consider a ΔPQR with ∠PQR = ∠PRQ.

We have to prove that PQ = PR.
Construction: Draw the bisector of ∠QPR and let it meet side QR at point S.
In ΔPSQ and ΔPSR, we have:
∠PQS = ∠PRS (Given)
PS = PS (Common side)
∠QPS = ∠RPS (∵ PS bisects ∠QPR)
So, by the AAS congruence rule, we obtain:
ΔPSQ ≅ ΔPSR
⇒ PQ = PR (By CPCT)
Hence, we have proved that the sides opposite equal angles of a triangle are also equal.
Example 2: DA and CB are equal perpendiculars to a line segment AB. Show that line segment CD bisects AB at point O.
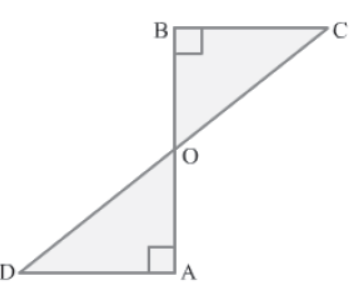
Solution:
In ΔDAO and ΔCBO, we have:
∠AOD = ∠BOC (Vertically opposite angles)
∠OAD = ∠OBC = 90° (∵ DA and CB are perpendiculars)
DA = CB (Given)
So, by the AAS congruence rule, we obtain:
ΔDAO ≅ ΔCBO
⇒ AO = BO (By CPCT)
Now, AO + BO = AB
Thus, line segment CD bisects line segment AB at point O.
Example 3: If two altitudes of a triangle are equal then show that the triangle is isosceles.
Solution:
Let us consider ΔPQR such that RT and QS are the equal altitudes drawn to the sides PQ and PR respectively.
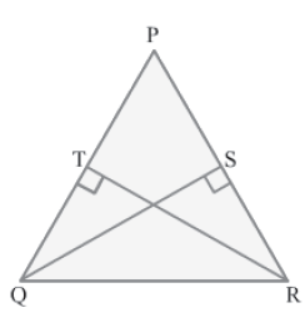
In ΔPTR and ΔPSQ, we have
∠PTR = ∠PSQ = 90°
∠TPR = ∠SPQ (Common angle)
RT = QS (Given)
So, by the AAS congruence rule, we obtain:
ΔPTR ≅ ΔPSQ
∴ PR = PQ (By CPCT)
Thus, ΔPQR is an isosceles triangle.
Example 1: In the given figure, ∠DBC = ∠EAC, ∠DCA = ∠ECB and BD = AE. Prove that BC = AC.

Solution:
It is given that ∠DCA = ∠ECB.
On adding ∠ECD to both sides of the above equation, we get:
∠DCA + ∠ECD = ∠ECB + ∠ECD
⇒ ∠ECA = ∠DCB… (1)
In ΔBDC and ΔAEC, we have:
∠DCB = ∠ECA (From equation 1)
∠DBC = ∠EAC (Given)
BD = AE (Given)
So, by the AAS congruence rule, we have:
ΔBDC ≅ ΔAEC
⇒ BC = AC (By CPCT)
Example 2: In the figure, ∠BAD = ∠BCE and AB = CB. Prove that ΔABD ≅ΔCBE.

Solution:
In ΔAOE and ΔCOD, we have:
∠EAO = ∠DCO (Given)
∠AOE = ∠COD (Vertically opposite angles)
∴ ∠AEO = ∠CDO … (1) [By the angle sum property]
Now,
∠AEO + ∠OEB = 180° (Linear pair)
∠CDO + ∠ODB = 180° (Linear pair)
∴ ∠AEO + ∠OEB = ∠CDO + ∠ODB
⇒ ∠AEO + ∠OEB = ∠AEO + ∠ODB (Using equation (1))
⇒ ∠OEB = ∠ODB
⇒ ∠CEB = ∠ADB … (2)
In ΔABD and ΔCBE, we have:
∠BAD = ∠BCE (Given)
∠ADB = ∠CEB (From equation 2)
AB = CB (Given)
So, by the AAS congruence rule, we have:
ΔABD ≅ ΔCBE
Example 3: Prove that if two triangles are congruent then their corresponding altitudes are equal.
Solution:
Let PS and XT be corresponding altitudes of congruent triangles ΔPQR and ΔXYZ.
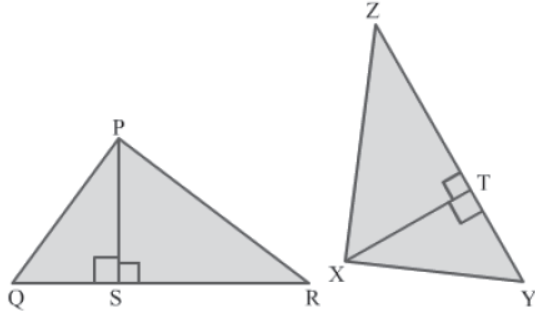
We have
ΔPQR ≅ ΔXYZ
∴ PQ = XY …(1) (By CPCT)
∠PQR = ∠XYZ …(2) (By CPCT)
In ΔPQS and ΔXYT, we have
∠PSQ = ∠XTY = 90°
∠PQR = ∠XYZ [From (2)]
PQ = XY [From (1)]
So, by the AAS congruence rule, we have:
ΔPQS ≅ ΔXYT
∴ PS = XT (By CPCT)
Thus, the corresponding altitudes of congruent triangles are equal.
Example 1: Are the following triangles congruent?
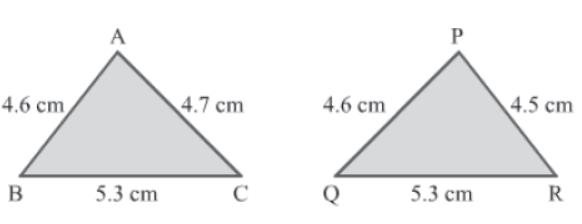
Solution:
In ΔABC and ΔPQR, we have:
AB = PQ = 4.6 cm
BC = QR = 5.3 cm
But AC ≠ PR
Therefore, ΔABC and ΔPQR are not congruent.
Example 2: ABCD is a rectangle with AC as one of its diagonals. Prove that the triangles formed on the two sides of diagonal AC are congruent.
Solution:
The required rectangle ABCD with AC as its diagonal can be drawn as is shown.
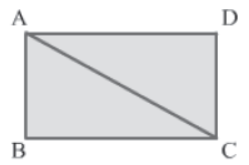
In ΔABC and ΔCDA, we have:
AB = CD (∵ Opposite sides of a rectangle are equal)
BC = DA (∵ Opposite sides of a rectangle are equal)
CA = AC (Common side)
Therefore, by the SSS congruence rule, we have:
ΔABC ≅ ΔCDA
Thus, the triangles formed on the two sides of diagonal AC are congruent.
Example 1: The given ΔABC is isosceles with AB = AC. AD is a median of the triangle. Prove that AD is perpendicular to BC.

Solution:
In ΔABD and ΔACD, we have:
AB = AC (Given)
BD = DC (∵ D is the midpoint of BC)
AD = AD (Common side)
Therefore, by the SSS congruence rule, we obtain:
ΔABD ≅ ΔACD
⇒ ∠ADB = ∠ADC (By CPCT)
Also, ∠ADB and ∠ADC form a linear pair.
So, ∠ADB + ∠ADC = 180°
⇒ ∠ADB + ∠ADB = 180° (∵ ∠ADB = ∠ADC)
⇒ 2∠ADB = 180°
⇒ ∠ADB = 90°
Thus, ∠ADB = ∠ADC = 90°, which means that AD is perpendicular to BC.
Example 2: ABCD is a parallelogram. If the diagonals of ABCD are equal, then find the measure of ∠ABC.
Solution:
The given parallelogram ABCD with equal diagonals AC and BD is shown below.

In parallelogram ABCD, we have:
AB = CD and AD = BC (∵ Opposite sides of a parallelogram are equal)
In ΔADB and ΔBCA, we have:
AD = BC (Proved above)
BD = AC (Given)
BA = AB (Common side)
So, by the SSS congruence rule, we have:
ΔADB ≅ ΔBCA
⇒ ∠BAD = ∠ABC … (1) [By CPCT]
Now, AD is parallel to BC and the transversal AB intersects them at A and B respectively.
We know that the sum of the interior angles on the same side of a transversal is
supplementary.
∴ ∠BAD + ∠ABC = 180°
⇒ ∠ABC + ∠ABC = 180° (By equation 1)
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
Example 1: In the given figure, ΔABC and ΔDBC are isosceles with AB = AC and DB = DC.
Prove that AD is the perpendicular bisector of BC.

Solution:
In ΔABD and ΔACD, we have:
AB = AC (Given)
DB = DC (Given)
AD = AD (Common side)
So, by the SSS congruence rule, we have:
ΔABD ≅ ΔACD
⇒ ∠BAE = ∠CAE … (1) [By CPCT]
In ΔBAE and ΔCAE, we have:
AB = AC (Given)
∠BAE = ∠CAE (From equation 1)
AE = AE (Common side)
So, by the SAS congruence rule, we have:
ΔBAE ≅ ΔCAE
⇒ BE = CE and ∠BEA = ∠CEA (By CPCT)
We know that ∠BEA + ∠CEA = 180° as they form a linear pair.
So, 2∠BEA = 180° (Proved above that ∠BEA = ∠CEA)
⇒ ∠BEA = 90°
Therefore, ∠BEA = ∠CEA = 90°
Since BE = CE and ∠BEA = ∠CEA = 90°, AD is the perpendicular bisector of BC.
Example 2: O is a point inside a square ABCD such that it is at an equal distance from points B and D. Prove that points A, O and C are collinear.
Solution:
The square with the given specifications is drawn as is shown.
Construction: Join point O to the vertices of the square.

In ΔAOD and ΔAOB, we have:
AD = AB (Sides of a square)
AO = AO (Common side)
OD = OB (Given)
So, by the SSS congruence rule, we have:
ΔAOD ≅ ΔAOB
⇒ ∠1 = ∠2… (1) [By CPCT]
Similarly, ΔDOC ≅ ΔBOC
⇒ ∠3 = ∠4 … (2) [By CPCT]
We know that:
∠1 + ∠2 + ∠ 3 + ∠4 = 360°
⇒ 2∠2 + 2∠3 = 360° (From equations 1 and 2)
⇒ ∠2 + ∠3 = 180°
Thus, ∠2 and ∠3 form a linear pair. Therefore, AOC is a line; in other words, points A, O and C are collinear.
Example 1: ΔABC and ΔLMN are right-angled at ∠ABC and ∠LMN respectively. In ΔABC, AB = 2.5 cm and AC = 4.5 cm. In ΔLMN, LN = 5.5 cm and LM = 2.5 cm. Examine whether the two triangles are congruent.
Solution: On the basis of the given information, the two triangles can be drawn as is shown.
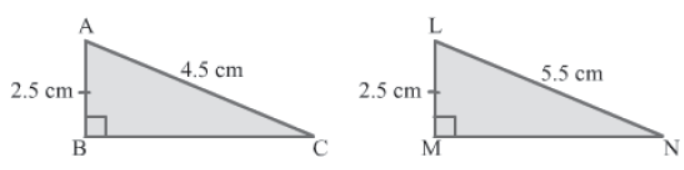
In ΔABC and ΔLMN, we have:
∠ABC = ∠LMN (Right angles)
AB = LM = 2.5 cm (Given)
But AC ≠ LN
Hence, ΔABC and ΔLMN are not congruent.
Example 2: Find the value of x if the shown triangles ABC and DEF are congruent.
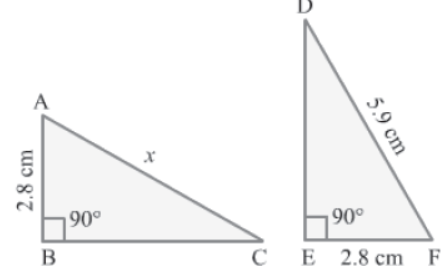
Solution:
It is given that ΔABC ≅ ΔDEF.
When two triangles are congruent, their corresponding sides are equal.
∴ AC = DF = 5.9 cm
Thus, the value of x is 5.9 cm.
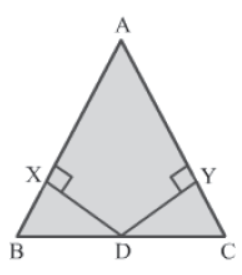
Example 1: In the given ΔABC, D is the midpoint of side BC. The perpendiculars DX and DY drawn from point D to sides AB and BC respectively are of the same length. Prove that DX and DY make the same angle with BC. IMG
Solution: On comparing ΔDXB and ΔDYC, we get:
DX = DY (Given)
∠DXB = ∠DYC = 90° (∵ DX and DY are perpendiculars)
BD = CD (∵ D is the midpoint of BC)
Thus, by the RHS congruence rule, we have:
ΔDXB ≅ ΔDYC
⇒ ∠BDX = ∠CDY (By CPCT)
Thus, the perpendiculars DX and DY make the same angle with side BC.
Example 2: In the given ΔABC, AD, BE and CF are the altitudes. If the three altitudes are equal, then prove that the triangle is equilateral.
Solution:
In ΔBEC and ΔCFB, we have:
BC = CB (Common side)
BE = CF (Given)
∠BEC = ∠CFB = 90° (∵ BE and CF are altitudes)
So, by the RHS congruence rule, we obtain:
ΔBEC ≅ ΔCFB
⇒ ∠BCE = ∠CBF (By CPCT)
⇒ ∠CBA = ∠BCA
⇒ AC = AB … (1) [∵ Sides opposite equal angles are equal]
Similarly, we can prove that ΔADB ≅ ΔBEA.
⇒ ∠DBA = ∠BAE (By CPCT)
⇒ ∠CBA = ∠BAC
⇒ AC = BC … (2) [∵ Sides opposite equal angles are equal]
From equations (1) and (2), we get:
AB = BC = AC
Hence, ΔABC is equilateral.
Example 1: If Z is a point equidistant from two lines m and n intersecting at point A, then prove that AZ bisects the angle between m and n.
Solution:
The following figure can be drawn as per the given information.
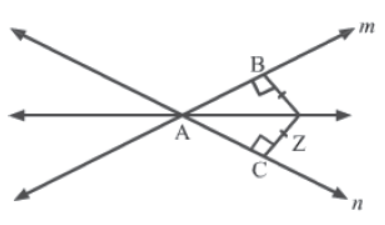
Construction: ZB and ZC are perpendiculars drawn from point Z to
lines m and n respectively.
Since Z is equidistant from m and n, we have:
ZB = ZC
In ΔZBA and ΔZCA, we have:
ZB = ZC (Proved above)
∠ZBA = ∠ZCA = 90° (∵ ZB and ZC are perpendiculars)
ZA = ZA (Common side)
So, by the RHS congruence rule, we have:
ΔZBA ≅ ΔZCA
⇒ ∠ZAB = ∠ZAC (By CPCT)
Now, ∠ZAB + ∠ZAC = ∠BAC
Therefore, AZ bisects the angle between lines m and n.
Example 2: In a ΔABC, BD = DC. If the perpendiculars from point D to sides AB and AC are equal, then prove that AB = AC.
Solution: The triangle with the given specifications is drawn below.

In ΔABC, D is the midpoint of BC. Also, DE and DF are the perpendiculars from D to AB and
AC respectively.
In ΔDEB and ΔDFC, we have:
∠DEB = ∠DFC = 90° (∵ DE and DF are perpendiculars)
DB = DC (Given)
DE = DF (Given)
So, by the RHS congruence rule, we obtain:
ΔDEB ≅ ΔDFC
⇒ ∠DBE = ∠DCF (By CPCT)
⇒ ∠CBA = ∠BCA
⇒ AC = AB (As sides opposite to equal angles are equal)
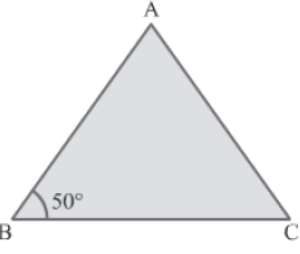
Example 1: In the given ΔABC, AB = AC. What is the measure of ∠BAC?
Solution:
ΔABC is an isosceles triangle with AB = AC.
By the property of isosceles triangles, we obtain:
∠ABC = ∠ACB
⇒ ∠ACB = 50°
By the angle sum property, we have:
∠ABC + ∠ACB + ∠BAC = 180°
⇒ 50° + 50° + ∠BAC = 180°
⇒ ∠BAC = 180° − 100°
⇒ ∠BAC = 80°
Example 2: Ram lives in a triangular tree house. The measure of each base angle is the same and the length of the base is 4 m. He wants to cover the slant sides with metal sheets. If the boundary of the triangular structure is 10 m, then what length of sheet does Ram need to cover the slant sides (irrespective of the width of the sheet).
Solution:
It is given that the base angles are equal; so, the triangular structure is isosceles. Hence, the
slant sides are equal.
Now, we know that:
Base = 4 m
Boundary of the triangular structure = Perimeter of the isosceles triangle = 10 m
⇒ 10 m = 4 m + 2 × (Measure of each slant side)
⇒ 2 × (Measure of each slant side) = 10 m − 4 m
⇒ 2 × (Measure of each slant side) = 6 m
Hence, Ram needs 6 m of metal sheet to cover the slant sides of the triangular structure.
Example 1: Find the missing angles in the following triangles.

Solution:
1. In ΔABC, AB = AC = 2.5 cm
Since the angles opposite equal sides of a triangle are equal, we obtain:
∠ABC = ∠ACB
Let ∠ABC = ∠ACB = x
By the angle sum property of triangles, we have:
∠ABC + ∠ACB + ∠BAC = 180°
⇒ x + x + 80° = 180°
⇒ 2x = 100°
⇒ x = 50°
Thus, ∠ABC = ∠ACB = 50°
2. In ΔPQR, PQ = QR = 5 cm and PR = 3 cm
Since PQ = QR, we obtain
∠QPR = ∠PRQ = 70°
Example 2: The shown ΔABC is isosceles with AB = AC. Find the measures of ∠BAC, ∠ABC and ∠ACB.

Solution: ∠ACB and exterior angle ∠ACD form a linear pair.
∴ ∠ACB + ∠ACD = 180°
⇒ x + 2x = 180°
⇒ 3x = 180°
⇒ ∴ x = 60°
So, ∠ACB = 60° and ∠ACD = 120°
ΔABC is isosceles.
∴ ∠ABC = ∠ACB = 60° (∵ Angles opposite equal sides are equal)
Now, by the exterior angle property, we have:
∠ACD = ∠BAC + ∠ABC
⇒ 120° = ∠BAC + 60°
⇒ ∠BAC = 60°
Thus, ∠BAC = ∠ABC = ∠ACB = 60°.
Example 3: Prove that in an isosceles triangle, the angle bisector of the apex angle is the perpendicular bisector of the base.
Solution:
Given: ABC is a triangle in which AB = AC and apex angle ∠A.
To Prove: AD is perpendicular bisector of BC and BD = DC.
Construction: Draw an angle bisector AD from A on BC.
Proof:

In ΔABD and ΔACD,
AB = AC (Given)
AD = AD (Common side)
∠BAD = ∠CAD (AD is a bisector of ∠A)
So, by SAS congruence criterion,
Δ ADB ≅ Δ ADC
⇒BD = DC and ∠ADB =∠ADC (CPCT)
Now,
∠ ADB + ∠ADC= 180° (Linear Pair)
⇒∠ ADB + ∠ ADB = 180°
⇒ 2∠ ADB = 180°
⇒ ∠ABD = 180°/2 = 90°
Thus, AD is the perpendicular bisector of BC.
Example 1: ΔABD is isosceles (figure not drawn to scale) with AB = BD, while ΔBCD is isosceles with BC = BD. Also, ∠BDC measures 70° and ∠ABC measures 90°. What is the measure of ∠ADC?
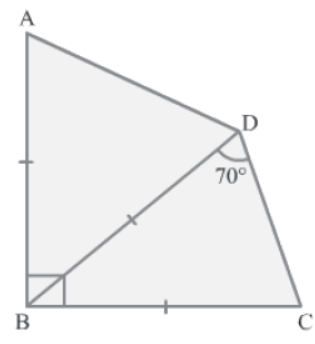
Solution:
In ΔBCD, BC = BD.
∴ ∠BCD = ∠BDC = 70º (∵ Angles opposite equal sides are equal)
In ΔBCD, by the angle sum property, we obtain:
∠BCD + ∠BDC + ∠CBD = 180º
⇒ 70º + 70º + ∠CBD = 180º
⇒ 140º + ∠CBD = 180º
⇒ ∠CBD = 40º
It is given that ∠ABC = 90º.
⇒ ∠ABD + ∠CBD = 90º
⇒ ∠ABD + 40º = 90º
⇒ ∠ABD = 50º
In ΔABD, we have:
AB = BD
∴ ∠BAD = ∠BDA = x (∵ Angles opposite equal sides are equal)
In ΔABD, by the angle sum property, we obtain:
∠ABD + ∠BAD + ∠BDA = 180º
⇒ 50º + x + x = 180º
⇒ 2x = 130º
⇒ x = 65º
So, ∠BAD = ∠BDA = 65º
Now,
∠ADC = ∠BDA + ∠CDB
⇒ ∠ADC = 65º + 70º
⇒ ∠ADC = 135º
Example 2: In the given figure, ΔPQR is isosceles with PQ = PR. Side SU is extended up to point V such that ST = SV. If ∠QTS = ∠RUS = 90°, prove that QS bisects ∠TSU and hence show that ΔQTS ≅ΔQVS.
Solution:
In ΔPQR, we have:
PQ = PR (Given)
∴ ∠PQR = ∠PRQ (∵ Angles opposite equal sides are equal)
It is given that ∠QTS = 90°.
Using the angle sum property in ΔQTS, we obtain:
∠TQS + ∠TSQ + ∠QTS = 180°
⇒ ∠TQS + ∠TSQ + 90° = 180°
⇒ ∠TSQ = 90° ∠TQS … (1)
It is given that ∠RUS = 90°.
Using the angle sum property in ΔRUS, we obtain:
∠SRU + ∠RUS + ∠RSU = 180°
⇒ ∠SRU + 90° + ∠RSU = 180°
⇒ ∠RSU = 90° – ∠SRU … (2)
∠SRU = ∠PRQ (Vertically opposite angles)
Also, ∠PQR = ∠PRQ
∴ ∠SRU = ∠PQR … (3)
Now, from equations (2) and (3), we get:
∠RSU = 90° – ∠PQR
⇒ ∠RSU = 90° – ∠TQS … (4) [∵ ∠PQR = ∠TQS]
From equations (1) and (4), we get:
∠TSQ = ∠RSU
Hence, QS bisects ∠TSU.
Now, consider ΔQTS and ΔQVS.
QS = QS (Common side)
∠TSQ = ∠QSV (∵ ∠TSQ = ∠RSU and ∠RSU = ∠QSV)
ST = SV (Given)
Thus, by the SAS congruency rule, we get:
ΔQTS ≅ ΔQVS
Example 1: In a ΔABC, ∠BAC = 2x and ∠ABC = ∠ACB = x. Find the value of x and hence show that AB = AC.
Solution:
It is given that ∠BAC = 2x and ∠ABC = ∠ACB = x.
By applying the angle sum property, we obtain:
∠BAC + ∠ABC + ∠ACB = 180°
⇒ 2x + x + x = 180°
⇒ 4x = 180°
⇒ x = 45°
So, ∠BAC = 2x = 2 × 45° = 90° and ∠ABC = ∠ACB = x = 45°
The given triangle can be drawn as is shown. IMG
We know that the sides opposite equal angles of a triangle are equal.
∴ AB = AC
Hence, ΔABC is isosceles with AB = AC.
Example 2: In the given ΔABC, ∠ABC = ∠ACB and the perimeter is 11 cm. Find the length of the base of the triangle.
Solution: It is given that ∠ABC = ∠ACB and AB = 3 cm.
We know that the sides opposite equal angles of a triangle are equal.
∴ AC = AB = 3 cm
Perimeter of ΔABC = AB + BC + AC
⇒ 11 cm = 3 cm + BC + 3 cm
⇒ BC = 5 cm
Thus, the length of the base of ΔABC is 5 cm.
Example 1: In the given ΔABC, ∠ABD = ∠ACD and AD is perpendicular to BC. Prove that AD bisects ∠BAC.
Solution:
In ΔABD and ΔACD, we have:
∠ABD = ∠ACD (Given)
∠ADB = ∠ADC = 90°
AB = AC (∵ Sides opposite equal angles are equal)
Thus, by the AAS congruence rule, we have:
ΔABD ≅ ΔACD
∴ ∠BAD = ∠CAD (By CPCT)
Thus, AD bisects ∠BAC.
Example 2: In the given ΔABC, ∠ABC = ∠ACB. Side BA is produced up to point D such that AB = AD. Prove that ∠BCD is a right angle.
Solution:
In ΔABC, we have:
∠ABC = ∠ACB … (1) [Given]
∴ AB = AC (∵ Sides opposite equal angles are equal)
Now,
AB = AD (Given)
AD = AC (∵ AB = AC)
Thus, in ΔADC, we have:
∠ACD = ∠ADC … (2) (∵ Angles opposite equal sides are equal)
On adding equations (1) and (2), we get:
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒ ∠BCD = ∠ABC + ∠BDC (∵ ∠ADC = ∠BDC)
On adding ∠BCD to both sides of the equation, we get:
∠BCD + ∠BCD = ∠ABC + ∠BDC + ∠BCD
⇒ 2∠BCD = 180° (By the angle sum property)
⇒ ∠BCD = 90°
Hence, ∠BCD is a right angle.
Example 1: The shown ΔPQR is isosceles with PQ = PR. QL and RM are the respective medians from vertices Q and R to sides PR and PQ. Prove that the medians have the same length.
Solution:
It is given that PQ = PR.
Also, QL and RM are medians.
∴ PL = LR and PM = MQ
So,
PL + LR = PR
LR + LR = PR
2LR = PR
LR = PR/2 … (1)
Similarly, MQ = PQ/2 … (2)
Since PQ = PR, using equations (1) and (2), we obtain:
LR = MQ … (3)
In ΔQRL and ΔRQM, we have:
LR = MQ (From (3))
∠LRQ = ∠MQR (∵ Angles opposite equal sides are equal)
QR = RQ (Common side)
∴ ΔQRL ≅ ΔRQM (By the SAS congruence criterion)
⇒ QL = RM (By CPCT)
Thus, the medians QL and RM have the same length.
Example 2: In a right-angled triangle ABC, ∠ACB = 2∠BAC. Prove that AC = 2BC.
Solution: The given ΔABC can be drawn as is shown.
Construction: Produce CB up to point D such that BD = BC. Join point A to point D. IMG
In ΔABD and ΔABC, we have:
BD = BC (By construction)
∠ABD = ∠ABC = 90°
AB = AB (Common side)
So, by the SAS congruence rule, we obtain:
ΔABD ≅ ΔABC
⇒ AD = AC and ∠DAB = ∠BAC (By CPCT)
Let ∠BAC be x. Then, ∠DAB will also be x.
Now, ∠DAC = ∠DAB + ∠BAC
⇒ ∠DAC = x + x
⇒ ∠DAC = 2x
⇒ ∠DAC = ∠ACB (∵ ∠ACB = 2∠BAC = 2x)
⇒ DC = AD (∵ Sides opposite equal angles are equal)
Since BC = DB, we have:
DC = 2BC
⇒ 2BC = AD
⇒ 2BC = AC (∵ We have proved AD = AC)
Example 1: In the given ΔPQR, PQ is greater than PR. Also, QS and RS are the respective bisectors of ∠PQR and ∠PRQ. Prove that ∠SRQ > ∠SQR.
Solution:
In ΔPQR, we have:
PQ > PR (Given)
⇒ ∠PRQ > ∠PQR (∵ Angle opposite longer side is greater)
⇒ ∠PRQ/2 > ∠PRQ/2
⇒ ∠SRQ > ∠SQR (∵ RS bisects ∠PRQ and QS bisects ∠PQR)
Example 2: ABC is an isosceles triangle with AB = AC and AB < BC. Prove that ∠BAC > ∠ABC.
Solution:
Consider the following ΔABC in which AB = AC and AB < BC.
In ΔABC, we have:
∠ABC = ∠ACB … (1) [∵ Angles opposite equal sides AB and AC are equal]
By the triangle inequality theorem, we have:
∠ACB < ∠BAC … (2) [∵ Angle opposite longer side BC is greater]
Thus, from (1) and (2), we obtain:
∠BAC > ∠ABC
Example 1: In the shown ΔABC, AB = 4 cm, BC = 5 cm and the perimeter is 16 cm.
Determine the smallest and greatest angles of the triangle.
Solution:
In ΔABC, we have:
AB = 4 cm and BC = 5 cm (Given)
Perimeter = 16 cm (Also given)
⇒ AB + BC + CA = 16 cm (∵ Perimeter is the sum of all sides)
⇒ 4 cm + 5 cm + CA = 16 cm
⇒ CA = 7 cm
Now, CA = 7 cm is the longest side of ΔABC. Thus, the angle opposite it, i.e., ∠ABC is the
greatest angle of the triangle.
∴ ∠ABC > ∠BAC and ∠ABC > ∠ACB … (1)
Also, BC > AB
∴ ∠BAC > ∠ACB … (2)
Thus, from (1) and (2), we can conclude that ∠ABC is the greatest angle and ∠ACB is the smallest angle in ΔABC.
Example 2: Suppose AB is the longest side and CD the shortest side of the given quadrilateral ABCD. Then, prove that ∠BCD > ∠BAD.
Solution:
In ΔABC, AB is the longest side.
So, AB > BC
⇒ ∠1 > ∠2 … (1) [∵ Angle opposite longer side is greater]
In ΔADC, CD is the shortest side.
So, AD > CD
⇒ ∠4 > ∠3 … (2) [∵ Angle opposite longer side is greater]
On adding (1) and (2), we get:
∠1 + ∠4 > ∠2 + ∠3
⇒ ∠BCD > ∠BAD
Example 1: In the given figure, PQ = PR. Show that ∠PRS > ∠PSR.
Solution:
In ΔPQR, we have:
PQ = PR
⇒ ∠PRQ = ∠PQR … (1) [∵ Angles opposite equal sides are equal]
In ΔPSQ, SQ is produced to R.
So, ∠PQR = ∠PSQ + ∠SPQ (By the exterior angle property)
⇒ ∠PQR > ∠PSQ … (2)
From (1) and (2), we obtain:
∠PRQ >∠PSQ
⇒ ∠PRS > ∠PSR (∵ ∠PRQ = ∠PRS and ∠PSQ = ∠PSR)
Example 2: In a ΔABC, AB > AC and AD is the bisector of ∠BAC. Show that ∠ADB > ∠ADC.
Solution: Let the following ΔABC be the given triangle such that AB > AC. Also, AD is the bisector of ∠BAC.
In ΔABC, we have:
AB > AC (Given)
⇒ ∠ACB > ∠ABC (∵ Angle opposite longer side is greater)
On adding ∠1 to both sides, we get:
∠ACB + ∠1 > ∠ABC + ∠1
⇒ ∠ACB + ∠2 > ∠ABC + ∠1 … (1) [∵ AD bisects ∠BAC; ∠1 = ∠2]
By the exterior angle property, we have:
∠ADB = ∠ACB + ∠2 … (2)
Similarly, ∠ADC = ∠ABC + ∠1 … (3)
Thus, by using (1), (2) and (3), we can conclude that:
∠ADB > ∠ADC
Example 1: The angles of a triangle are in the ratio 1 : 2 : 3. Find the greatest angle and identify the longest side of the triangle.
Solution:
It is given that the angles of the triangle, say ΔABC, are in ratio 1 : 2 : 3.
Let the angles be x, 2x and 3x, as is shown in the figure.
By the angle sum property of triangles, we have:
∠BAC + ∠ABC + ∠ACB = 180°
⇒ x + 3x + 2x = 180°
⇒ 6x = 180°
⇒ x = 30°
So, 2x = 2 × 30° = 60° and 3x = 3 × 30° = 90°
Thus, the greatest angle in the given triangle is ∠ABC, i.e., 90°.
Now, we know that the side opposite the greater angle is longer. In ΔABC, side AC is opposite the greatest angle; hence, it is the longest.
Example 2: Which side of the given triangle is the shortest?
Solution:
In order to find the shortest side of ΔDEF, we need to figure out the smallest angle of the
triangle. This is because the smallest side is opposite the smallest angle.
By the angle sum property of triangles, we have:
∠EDF + ∠DEF + ∠EFD = 180°
⇒ 48° + 87° + ∠EFD = 180°
⇒ 135° + ∠EFD = 180°
⇒ ∠EFD = 45°
Clearly, ∠EFD has the smallest measure in the given triangle. So, the side opposite it, i.e., DE is the shortest side of the triangle.
Example 1: In the given ΔABC, ∠ABD > ∠ACD and AD is the bisector of ∠BAC.
Prove that:
1. AB < AC
2. ∠ADB < ∠ADC IMG
Solution:
1. It is given that ∠ABD > ∠ACD.
∴ AC > AB (∵ Side opposite greater angle is longer)
Or, AB < AC
2. In ΔABD, we have:
∠ABD + ∠BAD + ∠ADB = 180° (By the angle sum property)
⇒ ∠ACD + ∠BAD + ∠ADB < 180° (∵ ∠ABD > ∠ACD)
⇒ ∠ACD + ∠CAD + ∠ADB < 180° (∵ AD bisects ∠BAC; ∠BAD = ∠CAD)
⇒ ∠ADB < 180° − (∠ACD +∠CAD)
⇒ ∠ADB < ∠ADC (By the angle sum property in ΔADC)
Example 2: Prove that of all the line segments that can be drawn to a given line from a point lying outside the line, the perpendicular line segment is the shortest.
Solution:
Let there be a straight line m, a point P lying outside the line and a point M lying on the line.
Also, PM ⊥ m and N is any point other than M on m.
Since PM is perpendicular to m, ∠PMN = 90°.
In ΔPMN, we have:
⇒ ∠PMN + ∠MPN + ∠PNM = 180° (By the angle sum property)
⇒ 90° + ∠MPN + ∠PNM = 180°
⇒ ∠MPN + ∠PNM = 90°
⇒ ∠PNM < 90°
⇒ ∠PNM < ∠PMN
⇒ PM < PN (∵ Side opposite greater angle is longer)
Thus, PM is the shortest of all line segments from point P to line m.
Example 1: In the given ΔPQR, ∠PQR = 50°, ∠PRQ = 20° and ∠PSQ = 30°. Prove that QS > SR.
Solution:
In ΔPQS, we have:
∠PQR = 50° and ∠PSQ = 30° (Given)
By using the angle sum property in ΔPQS, we obtain:
∠PQR + ∠PSQ + ∠QPS = 180°
⇒ 50° + 30° + ∠QPS = 180°
⇒ ∠QPS = 180° − (50° + 30°)
⇒ ∠QPS = 100°
So, ∠QPS > ∠PQR > ∠PSQ
Since the side opposite the greater angle is longer, we get:
QS > PS > PQ … (1)
∠PSQ and ∠PSR form a linear pair.
So, ∠PSQ + ∠PSR = 180°
⇒ 30° + ∠PSR = 180°
⇒ ∠PSR = 180° − 30°
⇒ ∠PSR = 150°
In ΔPSR, we have:
∠PSR + ∠SPR + ∠PRQ = 180° (By the angle sum property)
⇒ 150° + ∠SPR + 20° = 180°
⇒ ∠SPR = 180° − (150° + 20°)
⇒ ∠SPR = 10°
So, ∠PSR > ∠PRQ > ∠SPR
Since the side opposite the greater angle is longer, we get:
PR > PS > SR … (2)
By using (1) and (2), we can conclude that:
QS > SR
Example 2: Prove that the difference between any two sides of a triangle is less than the third side.
Solution:
We have to prove that the difference between any two sides of a triangle (let us say ΔABC) is less than the third side of the triangle. We will do so by showing that in ΔABC, BC − AC <
AB.
Construction: Extend side BA up to point D such that AD = AC. Join C to D. IMG
In ΔACD, we have:
AD = AC … (1)
We know that in an isosceles triangle, the angles opposite equal sides are equal.
∴ ∠ACD = ∠ADC
⇒ ∠ACD + ∠ACB > ∠ADC
⇒ ∠BCD > ∠ADC
We know that the side opposite the greater angle is longer. So, we obtain, BD > BC
⇒ AB + AD > BC (∵ BD = AB + AD)
⇒ AB + AC > BC (Using equation 1)
⇒ BC − AC < AB
Similarly, we can prove that AB − BC < AC and AC − AB < BC.
Thus, we have proved that the difference between any two sides of a triangle is less than the third side.


