Please refer to MCQ Questions Chapter 9 Sequences and Series Class 11 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 11 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 11 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 9 Sequences and Series in Class 11 Mathematics provided below to get more marks in exams.
Chapter 9 Sequences and Series MCQ Questions
Please refer to the following Chapter 9 Sequences and Series MCQ Questions Class 11 Mathematics with solutions for all important topics in the chapter.
Question: If a1, a2, a3,…. a20 are AM’s between 13 and 67, then the maximum value of a1 a2 a3 …a20 is equal to
(a) (20)20
(b) (40)20
(c) (60)20
(d) (80)20
Answer
B
Question: Jairam purchased a house in Rs. 15000 and paid Rs.5000 at once. Rest money he promised to pay in annual instalment of Rs. 1000 with 10% per annum interest. How much money is to be paid by Jairam ?
(a) Rs. 21555
(b) Rs. 20475
(c) Rs. 20500
(d) Rs. 20700
Answer
C
Question: Number of identical terms in the sequence 2, 5, 8, 11, … upto 100 terms and 3, 5, 7, 9, 11, … upto 100 terms, are
(a) 17
(b) 33
(c) 50
(d) 147
Answer
B
Question: If the sum of the roots of the equation ax2+ bx+ c = 0 be equal to the sum of the reciprocals of their squares, then bc2 ca2 ab2 will be in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
A
Question: If positive numbers a-1 b-1 c-1 , , are in AP, then the product of roots of the equation
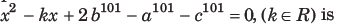
(a) > 0
(b) < 0
(c) = 0
(d) None of these
Answer
B
Question: If the set of natural numbers is partitioned into subsets S1= {1},=S2= {2,3),S3={456}S 1 and so on.
Then, the sum of the terms in S50 is
(a) 62525
(b) 25625
(c) 62500
(d) None of these
Answer
A
Question: 150 workers were engaged to finish a piece of work in a certain number of days. 4 workers dropped the second day, 4 more workers dropped the third day and so on. It takes eight more days to finish the work now. The number of days in which the work was completed is
(a) 15
(b) 20
(c) 25
(d) 30
Answer
C
Question: If p, q, r are in AP and are positive, the roots of the quadratic equation px2+qx+ r= 0 are all real for

Answer
A
Question: Concentric circles of radii 1, 2, 3, … , 100 cm are drawn. The interior of the smallest circle is coloured red and the angular regions are coloured alternately green and red, so that no two adjacent regions are of the same colour. Then, the total area of the green regions in sq cm is equal to
(a) 1000 π
(b) 5050 π
(c) 4950 π
(d) 5151π
Answer
B
Question: The sixth term of an AP is equal to 2. The value of the common difference of the AP which makes the product T1 T4 T5 least, is given by
(a) 8/5
(b) 5/4
(c) 2/3
(d) None of these
Answer
C
Question: After striking the floor, a certain ball rebounds (4/5)th of height from which it has fallen. Then, the total distance that it travels before coming to rest, if it is gently dropped from a height of 120 m is
(a) 1260 m
(b) 600 m
(c) 1080 m
(d) None of these
Answer
C
Question:
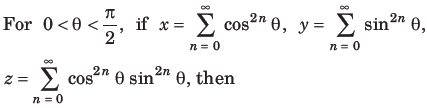
(a) xyz = xz + y
(b) xyz = xy + z
(c) xyz = x + y + z
(d) xyz = yz + x
Answer
B
Question: Let S = 8/5+16/65+…+128/218+1′ then
(a) S = 1088/545
(b) S = 545/1088
(c) S = 1056/545
(d) S = 545/1056
Answer
A
Question: The sum of n terms of an AP is a n(n – 1). The sum of the squares of these terms is
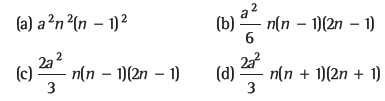
Answer
C
Question: The sum of the infinite terms of the series
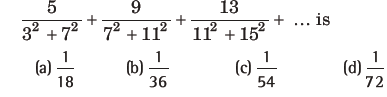
Answer
D
Question: If the decreasing GP is considered, then the sum of infinite terms is
(a) 64
(b) 128
(c) 256
(d) 729
Answer
B
Question: The sum of
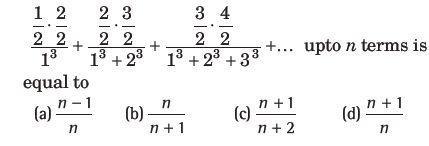
Answer
B
Question: If the sum of first n terms of an AP is cn2, then the sum of squares of these n terms is
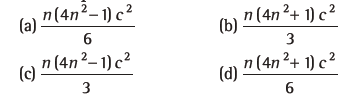
Answer
C
Question: If the ratio of AM between two positive real numbers a and b to their HM is m:n, then a:b is equal to
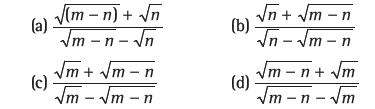
Answer
C
Question: If the non-zero numbers x, y, z are in AP and tan-1x, tan-1 y tan-1 z are in AP, then
(a) x = y = z
(b) y zx 2 =
(c) x yz 2 =
(d) z xy 2 =
Answer
B
Question: For an increasing AP a1, a2,…, an , if a1+ a3+ a5 = -12 and a1 a3 a5 = 80, then which of the following is/are true?
(a) a1 = -10
(b) a2 = -1
(c) a3 = – 4
(d) a5 = – 2
Answer
(a,c,d)
In a GP the sum of the first and last term is 66, the product of the second and the last but one is 128 and the sum of the terms is 126.
Question: If an increasing GP is considered, then the number of terms in GP is
(a) 9
(b) 8
(c) 12
(d) 6
Answer
D
Question:The consecutive digits of a three digit number are in GP. If the middle digit be increased by 2, then they form an AP. If 792 is subtracted from this, then we get the number constituting of same three digits but in reverse order. Then, number is divisible by
(a) 7
(b) 49
(c) 19
(d) None of these
Answer
(a,d)
Question: In any case, the difference of the least and greatest term is
(a) 78
(b) 126
(c) 127
(d) None of these
Answer
D
Question: What is the sum of the series 1– 1/2 + 1/4 – 1/8 + …..?
(a) 1/2
(b) 3/4
(c) 3/2
(d) 2/3
Answer
D
Question: If pth term of an AP is q, and its qth term is p, then what is the common difference ?
(a) – 1
(b) 0
(c) 2
(d) 1
Answer
A
Question: If 1, a and P are in A. P. and 1, g and P are in G. P., then
(a) 1 + 2a + g2 = 0
(b) 1 + 2a – g2 = 0
(c) 1 – 2a – g2 = 0
(d) 1 – 2a + g2 = 0
Answer
D
Question: If arithmetic mean of a and b is an+1 + bn+1 /an + bn , then the value of n is equal to
(a) –1
(b) 0
(c) 1
(d) 2
Answer
B
Question: If the nth term of the sequence is defined as an = 2n−3/6,then match the columns.
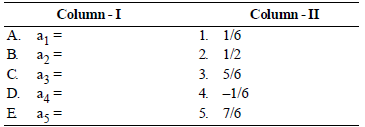
Codes
A B C D E
(a) 4 1 3 2 5
(b) 5 3 2 1 4
(c) 4 3 3 1 5
(d) 4 1 2 3 5
Answer
D
Question: The A.M. of the series 1, 2, 4, 8, 16, …, 2n is :
(a) 2n−1/n
(b) 2n+1−1/n+1
(c) 2n+1/n
(d) 2n−1/n+1
Answer
B
Question: 4th term from the end of the G.P. 3, 6, 12, 24., ………., 3072 is
(a) 348
(b) 843
(c) 438
(d) 384
Answer
D
Question: The Fibonacci sequence is defined by 1 = a1 = a2 and an = an – 1 + an – 2, n > 2. Then value of an + 1/an for n = 2, is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question: Assertion: The ratio of sum of m terms to the sum of n terms of an A.P is m2 : n2. If Tk is the kth term, then T5/T2 = 3.
Reason: For nth term, tn = a + (n – 1)d, where ‘a’ is first term and ‘d’ is common difference.
Answer
B
Question: Assertion: Value of a17, whose nth term is an = 4n – 3, is 65.
Reason: Value of a9, whose nth term is an = (–1)n–1.n3.
Answer
B
Question: Assertion: If the third term of a G.P. is 4, then the product of its first five terms is 45.
Reason: Product of first five terms of a G.P. is given as a (ar) (ar2) (ar3) (ar4)
Answer
A
Question: Assertion: For x = ± 1, the numbers −2/7, x, −7/2 are in G.P.
Reason: Three numbers a, b, c are in G.P. if b2 = ac.
Answer
A
Question: Assertion: If the sum of n terms of an A.P. is 3n2 + 5n and its mth term is 164, then the value of m is 27.
Reason: 20th term of the G.P. 5/2, 5/4, 5/8, … is 5/220
Answer
B
Question: Assertion: If each term of a G.. P. is multiplied or divided by some fixed non-zero number, the resulting sequence is also a G. P.
Reason: If –1 < r < 1, i.e. | r | < 1, then the sum of the infinite G. P., a + ar + ar2 + …………..= a/1−r
i.e., S∞ = a/1−r
Answer
B
Question: Let sum of n terms of a series Sn = 6n2 + 3n + 1.
Assertion: The series Sn is in A.P.
Reason: Sum of n terms of an A.P. is always of the form an2 + bn.
Answer
D
STATEMENT TYPE QUESTIONS
Each of these questions contains two
statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c), (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question: Statement I The sums of n terms of two arithmetic progressions are in the ratio (7n + 1) : (4n + 17), then the ratio of their nth terms is 7 : 4.
Statement II If Sn= ax2+bx+c, then
Tn=Sn-Sn-1
Answer
D
Question: Consider first three terms of a sequence Sn is |x – 1|, 3,|x – 3|, which are in AP.
Statement I The sixth term of Sn is 7 < third term.
Statement II If a, a + d, a + 2d, . . . are in AP (d≠ 0),
then sixth term is (a + 5d).
Answer
D
Question: Statement I 3, 6, 12 are in GP, then 9, 12, 18 are in HP.
Statement II If middle term is added in three consecutive terms of a GP, resultant will be in HP.
Answer
A
Question: Let sum of n terms of a series Sn = 6n2+3n+1
Statement I The series Sn is in AP.
Statement II Sum of n terms of an AP is always of the form an2 +bn.
Answer
D
Question:Statement I There are infinite geometric progressions for which 27, 8 and 12 are three of its terms (not necessarily consecutive).
Statement II Given terms are integers.
Answer
B
Question: Let us define the sum of cubic number is
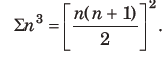
Statement I Sum of the series
13-23+33-43+…+113=378
Statement II For any odd integer
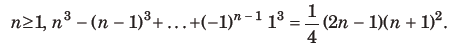
Answer
D
Question:
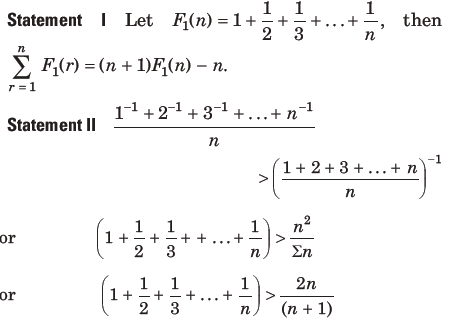
Answer
B
Question: Statement I If the AM of two numbers is 5/2, GM of the numbers is 2, then the HM will be 8/5.
Statement II For a group of positive numbers (GM)2 = (AM)x (HM).
Answer
C
Question: Statement I The sum of the series
1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + . . .+ (361 + 380 + 400) is 8000.
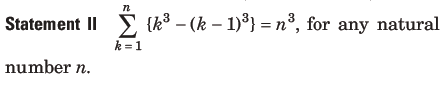
Answer
A
Question: If 100 times the 100th term of an AP with non-zero common difference equals the 50 times its 50th term, then the 150th term of this AP is
(a) –150
(b) 150 times its 50th term
(c) 150
(d) zero
Answer
D
Question: The sum of the infinity of the series
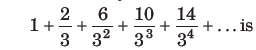
(a) 3
(b) 4
(c) 6
(d) 2
Answer
A
Question: A man saves Rs.200 in each of the first three months of his service. In each of the subsequent months his saving increases by Rs.40 more than the saving of immediately previous month. His total saving from the start of service will be Rs.11040 after
(a) 19 months
(b) 20 months
(c) 21 months
(d) 18 months
Answer
C
Question: The sum of first 20 terms of the sequence 0.7, 0.77, 0.777, … , is
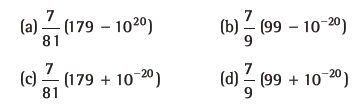
(a)7/81(179- 1020
(b)7/9(99-10– 20)
(c)7/81(179+ 10 -20)
(d)7/9(99+ 10– 20)
Answer
C
Question: A person is to count 4500 currency notes. Let an denotes the number of notes he counts in the nth minute. If a1= a2=…=a10=150 and a10, a11, . . . are in AP with common difference –2, then the time taken by him to count all notes, is
(a) 24 min
(b) 34 min
(c) 125 min
(d) 135 min
Answer
B
Question: If p and q are positive real numbers such that p q 2 2 + = 1, then the maximum value of ( p + q) is
(a) 2
(b) 1/2
(c) 1/√2
(d) 2√2
Answer
D
Question: The first two terms of a geometric progression add upto 12. The sum of the third and the fourth terms is 48. If the terms of the geometric progression are alternately positive and negative, then first term is
(a) 4
(b) –4
(c) –12
(d) 12
Answer
C
Question: In a geometric progression consisting of positive terms, each term equals the sum of the next two terms. Then, the common ratio of this progression is equal to
(a)1/2(1-√5)
(b)1/2√5
(c) √5
(d)1/2(√5-1
Answer
D
Question:
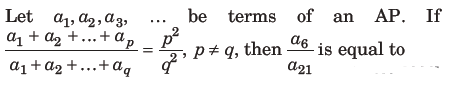
(a)7/2
(b)2/7
(c)11/41
(d)41/11
Answer
C
Question:

Answer
C
Question:
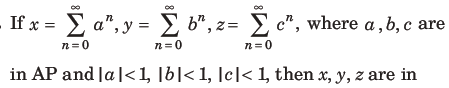
(a) HP
(b) AGP
(c) AP
(d) GP
Answer
A

