Please refer to MCQ Questions Chapter 5 Complex Numbers and Quadratic Equations Class 11 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 11 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 11 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 5 Complex Numbers and Quadratic Equations in Class 11 Mathematics provided below to get more marks in exams.
Chapter 5 Complex Numbers and Quadratic Equations MCQ Questions
Please refer to the following Chapter 5 Complex Numbers and Quadratic Equations MCQ Questions Class 11 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 5 Complex Numbers and Quadratic Equations Class 11 Mathematics
Question. If in polar form z1 = (1, α), z2= (1, β), z3 = (1, γ) and z1 + z2 + z3 = 0, then z̄1 + z2 + z3 is equal to
(a) 1
(b) 0
(c) –1
(d) None of these
Answer
B
Question. The value of x4 +9x3+35x2 -x + 4 for x = – 5 + 2√-4 is
(a) 0
(b) –160
(c) 160
(d) –164
Answer
B
Question. If α = cos (2π/7) + isin(2π/7) then the qua dratic equa tion whose roots are α = a +a2 + a4 and β = a3 + a5 + a6 is
(a) x2 – x + 2 = 0
(b) x2 + x – 2 = 0
(c) x2 – x – 2 = 0
(d) x2 + x + 2 = 0
Answer
D
Question. Given that the equa tion z2 +( p+iq) z + r is = 0, where p, q, rand s are real and non-zero roots, then
(a) pqr = r2 + p2s
(b) prs = q2 + r2p
(c) qrs = p2 + s2q
(d) pqs = s2 + q2r
Answer
D
Question. If |z – iRe ( z)|=|z – Im ( z)| (where i = √-1), then z lies on
(a) Re (z) = 2
(b) Im (z) = 2
(c) Re (z) + Im (z) = 2
(d) None of the above
Answer
D
Question. If z1 z2 and be complex numbers such that z1 ≠ z2 and|z1| = |z2| If z1 has positive real part and z2 has negative imaginary part, then [( z1 + z2 )/( z1 – z2 )]may be
(a) purely imaginary
(b) real and positive
(c) real and negative
(d) None of the above
Answer
A
Question. If |z1| |z2| = , arg (z1 /z2 ) = p, then z1 + z2 is equal to
(a) 0
(b) purely imaginary
(c) purely real
(d) None of these
Answer
A
Question. If |z|<√2 – 1, then |z2 + 2zcosα | is
(a) less than 1
(b) 2 + 1
(c) 2 – 1
(d) None of these
Answer
A
Question. If ω =z /z-i/3 and |w|= 1, then z lies on
(a) a parabola
(b) a straight line
(c) a circle
(d) an ellipse
Answer
B
Question. The imag i nary part of
( z – 1)(cos – i sin ) + ( z – 1)- ´ (cos + i sin ) a a 1 a a is zero, if
(a) |z – 1 | = 2
(b) arg (z – 1) = 2a
(c) arg (z – 1) = a
(d) |z | = 1
Answer
C
Question. If cos a + cos b + cos g = sin a + sin b + sin g = 0, then cos 3a + cos 3 b + cos 3 g is equal to
(a) 0
(b) cos (a + b + g)
(c) 3 cos (a + b + g)
(d) 3 sin(a + b + g)
Answer
C
Question. Let z1 and z2 be two roots of the equa tion z2 + az + b = 0, be ing com plex. Fur ther, as sume that the or i gin z1 and z2 form an equi lat eral tri an gle.
Then,
(a) a2 = b
(b) a2 = 2b
(c) a2 = 3b
(d) a2 = 4b
Answer
C
Question. If A(z1), B(z2) and C(z3) are the vertices of the DABC such that ( z1 – z2 )/( z3 – z2 ) = (1√2) – (i1√2) , then ΔABC is
(a) equilateral
(b) right angled
(c) isosceles
(d) obtuse angled
Answer
C
Question. If z1 , z2 , z3 and are the vertices of an equilateral ΔABC such that |z1 – i| |z2 -i| |z3 – i|, then
|z1 + z2 + z3 | is equal to
(a) 3√3
(b) √3
(c) 3
(d) 1/3√3
Answer
C
Question. If z1 = a + ib and z2 = c+id 2 are com plex num bers such that |z1| |z2|= 1 and Re( z1z2 ) = 0 then the pair of com plex num bers ω1 = a + ic and ω2 = b + id satisfies
(a) |w1| = 1
(b) |w2 | = 1
(c) Re|w1w2 | = 0
(d) None of these
Answer
(a,b,c)
Question. If |z1| |z2| = 1 and amp z1 + amp z2 = 0, then
(a) z1z2 = 1
(b) z1 + z2 = 0
(c) z1 = z2
(d) None of these
Answer
(a,c)
Question. If |z1| 1 = 15 and |z2– 3 – 4i|= 5 then
(a) | z1 – z2 |min = 5
(b) | z1 – z2 |min = 10
(c) | z1 – z2 |max = 20
(d) | z1 – z2 |max = 25
Answer
(a,d)
Question. Complex number z1 z̄2 is
(a) purely real
(b) purely imaginary
(c) zero
(d) None of the above
Answer
B
Question. Complex number z1/z2 / is
(a) purely real
(b) purely imaginary
(c) zero
(d) None of these
Answer
B
Question. One of the possible argument of complex number i( z1 / z2 )
(a) π/2
(b) – π/2
(c) 0
(d) None of these
Answer
C
Question. If z is a complex number of unit modulus and argument θ, then arg (1+z/1+z) is equal to
(a) -q
(b) π/2 -θ
(c) q
(d) π – q
Answer
C
Question. If z ≠ 1 and z2/z-1 is real, then the point represented by the complex number z lies
(a) either on the real axis or on a circle passing through the origin
(b) on a circle with centre at the origin
(c) either on the real axis or on a circle not passing through the origin
(d) on the imaginary axis
Answer
A
Question. If w(≠ 1) is a cube root of unity and (1 )+ w 7 = A + Bw .
Then, (A, B) is equal to
(a) (1, 1)
(b) (1, 0)
(c) (-1, 1)
(d) (0, 1)
Answer
A
Question. The equa tion zz̄ + (2 – 3 i) z + (2 + 3 i)z̄ + 4 = 0 rep re sents a cir cle of ra dius
(a) 2
(b) 3
(c) 4
(d) 6
Answer
B
Question. When z+i/z+2 is purely imag i nary, the lo cus de scribed by the point z in the ar gand di a gram is a
(a) circle of radius √5/2
(b) circle of radius 5/4
(c) straight line
(d) parabola
Answer
A
Question. The number of complex numbers z such that |z – 1|=|z + 1|=|z – i| is equal to
(a) 0
(b) 1
(c) 2
(d) ∞
Answer
B
Question. If |z-4/z| =2 then the maximum value of| z| is equal to [AIEEE 2009]
(a) √3 + 1
(b) √5 + 1
(c) 2
(d) 2 +√2
Answer
B
Question. If |z + 4|£ 3, then the max i mum value of |z + 1| is
(a) 4
(b) 10
(c) 6
(d) 0
Answer
C
Question. If the cube roots of unity are 1 2 , wand w , then the roots of the equa tion (x – 1) + 8 = 0, 3 are
(a) -1 1 + 2ω 1 + 2ω2
(b) -1 1 – 2ω – 2 , 1-2ω2
(c) -1, -1, -1
(d) -1 -1 + 2ω -1 – 2ω2
Answer
B
Question. If (1+i/1-i)x = 1 then
(a) x = 4n, where n is any positive integer
(b) x = 2n, where n is any positive integer
(c) x = 4n + 1, where n is any positive integer
(d) x = 2n + 1, where n is any positive integer
Answer
A
Question. If ω is an imag i nary cube root of unity, then (1 + ω – ω2) 7 is equal to
(a) 128 ω
(b) -128 ω
(c) 128 ω2
(d) -128 ω2
Answer
D
Question. If z = r(cos θ + i sin θ), then the value of z/z̄ + z̄/z is
(a) cos 2θ
(b) 2 cos 2θ
(c) 2 cos θ
(d) 2 sin θ
Answer
B
Question. sin x + i cos 2x and cos x – i sin 2x are conjugate to each other for
(a) x = nπ
(b) x = (n + 1/2) π/2
(c) x = 0
(d) No value of x
Answer
D
Question. arg z̄ + arg z; z ≠ 0 is equal to :
(a) π/4
(b) π
(c) 0
(d) π/2
Answer
C
Question. If z = x + iy, z1/3 = a – ib and x/a – y/b = k(a2 – b2), then value of k equals
(a) 2
(b) 4
(c) 6
(d) 1
Answer
B
Question. If z = 3–i/2+i +3+i/2–i , then value of arg (zi) is
(a) 0
(b) π/6
(c) π/3
(d) π/2
Answer
D
Question. If (1–i /1+i)100 = a+ib then
(a) a = 2, b = – 1
(b) a = 1, b = 0
(c) a = 0, b = 1
(d) a = – 1, b = 2
Answer
B
Question. Simplify the complex numbers given in column-I and match with column-II.

Codes:
A B C
(a) 1 2 3
(b) 2 1 3
(c) 3 1 2
(d) 2 3 1
Answer
D
Question. If a root of the equations x2 + px + q = 0 and x2 + αx + β = 0 is common, then its value will be (where p ≠ α and q ≠ β)
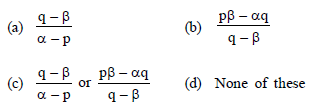
Answer
C
Question. If one root of the equation x2 + px +12 = 0 is 4, while the equation x2 + px + q = 0 has equal roots , then the value of ‘q’ is
(a) 4
(b) 12
(c) 3
(d) 49/4
Answer
D
Question. The number of real roots of (x + 1/x)3 + (x + 1/x) = 0 is
(a) 0
(b) 2
(c) 4
(d) 6
Answer
A
Question. If 4x + i(3x – y) = 3 + i(–6), where x and y are real numbers, then the values of x and y are
(a) x= 3/5 and y= 33/4
(b) x= 3/4 and y= 22/3
(c) x= 3/4 and y= 33/4
(d) x= 3/4 and y= 33/5
Answer
C
Question. If the roots of 4x2 + 5k = (5k + 1)x differ by unity, then the negative value of k is
(a) –3
(b) –5
(c) – 1/5
(d) – 3/5
Answer
C
Question. Value of (cosθ+ isinθ)4/(cosθ– isinθ)3is
(a) cos 5θ + i sin 5θ
(b) cos 7θ + i sin 7θ
(c) cos 4θ + i sin 4θ
(d) cosθ + i sin θ
Answer
B
Question. If | z2 – 1| = |z |2 + 1, then z lies on
(a) imaginary axis
(b) real axis
(c) origin
(d) None of these
Answer
A
Question. 1 + i2 + i4 + i6 + … + i2n is
(a) positive
(b) negative
(c) 0
(d) cannot be determined
Answer
D
Question. If z = 2 + i, then (z – 1) (z̄ – 5) + (z̄ – 1) (z – 5) is equal to
(a) 2
(b) 7
(c) –1
(d) –4
Answer
D
Question. Sum of all real roots of the equation | x – 2 | 2 + | x – 2 | – 2 = 0 is
(a) 2
(b) 4
(c) 5
(d) 6
Answer
B
Question. The value of (z + 3) (z + 3) is equivalent to
(a) |z + 3|2
(b) |z – 3|
(c) z2 + 3
(d) None of these
Answer
A
Question. If z = i9 + i19, then z is equal to a + ai. The value of ‘a’ is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. Roots of x2 + 2 = 0 are ± n i . The value of n is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. A number z = a + ib, where a and b are real numbers, is called
(a) complex number
(b) real number
(c) natural number
(d) integer
Answer
A
Question. The modulus of √2i – √–2i is:
(a) 2
(b) √2
(c) 0
(d) 2√2
Answer
A
Question. If z = 2 – 3i, then the value of z2 – 4z + 13 is
(a) 1
(b) –1
(c) 0
(d) None of these
Answer
C
Question. If a > 0, b > 0, c > 0, then both the roots of the equation ax2 + bx + c = 0.
(a) Are real and negative
(b) Have negative real parts
(c) Are rational numbers
(d) None of these
Answer
B
Question. The multiplicative inverse of 3 + 4i/4 – 5i is
(a) 8/25 – 31/25 i
(b) – 8/25 – 31/25 i
(c) – 8/25 + 31/25 i
(d) None of these
Answer
B
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, Reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, Reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, Reason is incorrect
(d) Assertion is incorrect, Reason is correct.
Question. Assertion : Let f(x) be a quadratic expression such that f(0) + f(1) = 0. If –2 is one of the root of f(x) = 0, then other root is 3/5.
Reason : If α and β are the zeroes of f(x) = ax2 + bx + c, then sum of zeroes =– b/a , product of zeroes = c/a
Answer
A
Question. Assertion : Consider z1 and z2 are two complex numbers such that |z1| = |z2| + |z1 – z2|, then Im (z1/z2) = 0.
Reason : arg(z) = 0 ⇒ z is purely real.
Answer
A
Question. Assertion : If |z1 + z2|2 = |z1|2 + |z2|2, then z1/z2 is purely imaginary.
Reason : If z is purely imaginary, then z + z̄ = 0.
Answer
B
Question. Assertion : If P and Q are the points in the plane XOY representing the complex numbers z1 and z2 respectively, then distance |PQ| = |z2 – z1|.
Reason : Locus of the point P(z) satisfying |z – (2 + 3i)| = 4 is a straight line.
Answer
C
Question. Assertion : The greatest integral value of λ for which (2λ – 1)x2 – 4x + (2λ – 1) = 0 has real roots, is 2.
Reason : For real roots of ax2 + bx + c = 0, D ≥ 0.
Answer
D
Question. Assertion : The equation ix2 – 3ix + 2i = 0 has non-real roots.
Reason : If a, b, c are real and b2 – 4ac ≥ 0, then the roots of the equation ax2 + bx + c = 0 are real and if b2 – 4ac < 0, then roots of ax2 + bx + c = 0 are non-real.
Answer
D

We hope you liked the above provided MCQ Questions Chapter 5 Complex Numbers and Quadratic Equations Class 11 Mathematics with solutions. If you have any questions please ask us in the comments box below.


