Assignments For Class 10 Mathematics Circles

Assignments for Class 10 Mathematics Circles have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Circles from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Circles. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Circles book and get good marks in class 10 exams.

CBSE Class 10 Mathematics Circles Assignment Set A

CBSE Class 10 Mathematics Circles Assignment Set B

CBSE Class 10 Mathematics Circles Assignment Set C

CBSE Class 10 Mathematics Circles Assignment Set D

CBSE Class 10 Mathematics Circles Assignment Set E

CBSE Class 10 Mathematics Circles Assignment Set F

CBSE Class 10 Mathematics Circles Assignment Set G

CBSE Class 10 Mathematics Circles Assignment Set H

CBSE Class 10 Mathematics Circles Assignments Set A

CBSE Class 10 Mathematics Circles Assignments Set B

CBSE Class 10 Mathematics Circles Assignments Set C

CBSE Class 10 Mathematics Circles Assignments Set D

CBSE Class 10 Mathematics Circles Assignments Set E

CBSE Class 10 Mathematics Circles Assignments Set F

CBSE Class 10 Mathematics Circles Assignments Set G

Circles

The perimeter of the circle is referred to as the circumference of the circle.

• A secant divides a circle in two parts and a tangent touches a circle.
• There is one and only one tangent at a point of the circle.
  There can be maximum two number of tangents which can be drawn to the circle from any given external point.
  The length of two tangents from an external point to a circle is equal. 

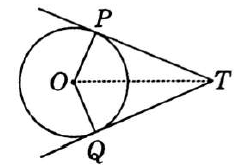
The tangent to a circle is perpendicular to the radius through the point of contact. 

PRACTICE EXERCISE

Question. Circles are drawn from the three vertices of a ΔABC (as shown); taken as centre to touch each other externally. If the sides of the triangle are 4 cm, 6 cm and 8 cm, find the radii of the circles.   

Solution. 3 cm, 5 cm and 1 cm

Question. The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of a bigger circle. BD is a tangent to the smaller circle, touching it at D. Find the length AD. 

Solution. 19 cm

Question. Find the length of the tangent drawn from a point whose distance from the centre is 25 cm when the radius of the circle is 24 cm.   
Solution. 7 cm

Question. In the given figure, the four sides AB, BC, CD and DA of a quadrilateral ABCD touches a circle at the points P, Q, R and S respectively. If AB = 6 cm, BC = 7 cm and CD = 4 cm, find AD.   

Solution. 3 cm

Question. A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
Solution. 5 cm

Question. A point P is 29 cm from the centre of the circle. Find the length of the tangent drawn from P to the circle if the radius of the circle is 20 cm.
Solution. 21 cm

Question. P and Q are centres of circles of radii 9 cm and 2 cm respectively. PQ = 17 cm. R is the centre of a circle of radius x cm which touches the above circles externally. Given that ΔPRQ = 90°, write an equation in x and solve it.
Solution. x² + 11x – 10² = 0; x = 6

Question. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. (see figure). Find the length of TP.   

Solution. TP = 20/3 cm

Question. A circle is inscribed in a ΔABC having sides 8 cm, 10 cm and 12 cm as shown. Find the length of AD, BE and CF.   

Solution. AD = 3 cm, BE = 7 cm and CF= 5 cm

Question. In the given fig. P, Q and R are the points of contact. If AB = 4 cm, BP = 2 cm then the perimeter of ΔABC is     

Solution. 12 cm

Question. The distance between two tangent parallel to each other to a circle is 12cm. The radius of circle is
Solution. 6 cm

Question. In the given fig. O is the centre of the circle and PQ is tangent then ∠POQ + QPO is equal to 

Solution. 90°

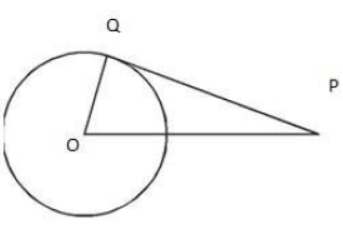
Question. If PQ is a tangent to a circle of radius 5cm and PQ = 12 cm, Q is point of contact, then OP is   
Solution. √119 cm

Question. How many tangents can a circle have?
Solution. Infinite

Question. In the given fig. QS is a tangent to the circle, OS = 8 cm, OQ = 6 cm then the length of QS is 

Solution. √28 cm

Question. In the given fig PQ is tangent to outer circle and PR is tangent to inner circle. If PQ = 4 cm, OQ = 3 cm and OR = 2 cm then the length of PR is     

Solution. √21 cm

Question. How many tangents can be drawn from a given exterior point to a circle?
Solution. Only 2 Tangents

Question. The chord of a circle of radius 10cm subtends a right angle at its centre. Find the length of the chord.
Solution. 10√2

Question. In the given fig. PQ and PR are tangents to the circle, QOP= 70°, then QPR is equal to 

Solution. 40°

Question. If AB, AC, PQ are tangent in the given figure, and AB = 5 cm, find the perimeter of ΔAPQ.   

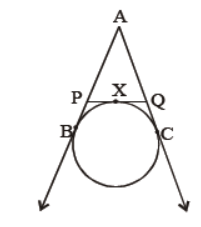
Solution. 10 cm

Question. ABCD is a quadrilateral such that ∠A = 90°. A circle with centre O, touches the sides AB, BC, CD and DA at E, F, G, H respectively. If CD = 35 cm, AD = 20 cm and CF = 25 cm. Find the radius of the circle.
Solution. 10 cm

Question. ABC is a right angle triangle, right angled at A, AB = 6 cm and AC = 8 cm. A circle with centre O is inscribed inside the triangle. Calculate the value of ‘r’, the radius of the inscribed circle. 
Solution. r = 2 cm

Question. ABCD is a quadrilateral such that ∠A = 90°. A circle with center O, touches the sides AB, BC, CD and DA at E, F, G, H respectively. If CD = 30 cm, AD = 15 cm and CF = 20 cm, find the radius of the circle.
Solution. 5 cm

Question. PQ and RS are two parallel tangents to a circle with centre O and another tangent XY, with point of contact C intersects PQ at A and RS at B. Prove that ΔAOB = 90°. 
Solution. Join O to A, O to B and O to C.   
Since tangent is perpendicular to the radius through the point of contact.

Question. PQR is a right-angled triangle right angled at Q with PQ = 16 cm, QR = 12 cm. A circle with centre at O and radius r is inscribed in ΔPQR. Find the value of r.
Solution. Let the circle touch the sides QR, RP and PQ of ΔPQR at the points A, B and C respectively. Join O to A and O to C.   

Then, OC = OA = r cm. 
In ΔPQR, using pythagoras theorem,
PR² = PQ² + QR²
= 162 + 122 = 256 + 144 = 400
∴ PR = 20 cm.
Since OC is the radius and PQ is the tangent at C, we have ΔOCQ = 90°. Similarly, ΔOAQ = 90°.
Also, ΔAQC = 90° [∴ given]
Hence, the remaining angle AOC of quadrilateral AQCO is also 90°.
Again, QA = QC [∴ lengths of the tangents from the external point to a circle are equal]
∴ The quadrilateral AQCO is a square.
∴ QC = QA = r cm
Hence, PC = (16 – r) cm and RA = (12 – r) cm.
Now, PB = PC (∴ same as above)
Similarly, RB = RA = (12 – r) cm
⇒ PB + RB = (16 – r + 12 – r) cm = (28 – 2r) cm
⇒ PR = (28 – 2r) cm
⇒ 20 cm = (28 – 2r) cm
⇒ 2r = 28 – 20 = 8
⇒ r = 4
Hence, the required length of the radius of the circle is 4 cm. Ans.

Question. The radius of the incircle of a triangle is 4 cm and the segments into which one side is divided by the point of contact are 6 cm and 8 cm. Determine the other two sides of the triangle. 
Solution. Since lengths of tangent from an external point to the circle are equal.   
∴ BP = BR = 8 cm
CP = CQ = 6 cm
and, AR = AQ = x cm (say)
Also, IP = IQ = IR = 4 cm
Now, 2s = a + b + c
⇒ 2s = 8 + 6 + 6 + x + x + 8
⇒ 2s = 28 + 2x

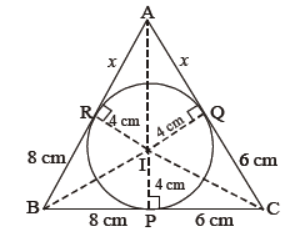
⇒ s = 14 + x
⇒ s – a = 14 + x – 14 = x, s – b = 14 + x – 6 – x = 8 and
s – c = 14 + x – 8 – x = 6.
Clearly, ar (ΔABC) = ar (ΔIBC) + ar (ΔICA) + ar (ΔIAB)

Squaring both sides, we get
3x (14 + x) = (14 + x)²
⇒ 3x = 14 + x [∴ 14 + x ≠ 0]
⇒ 2x = 14 ⇒ x = 7
⇒ AB = (8 + 7) cm = 15 cm and AC = (6 + 7) cm = 13 cm. Ans.

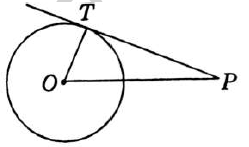
Question. A point P is 26 cm away from the centre O of a circle and the length PQ of the tangent segment drawn from P to the circle is 10 cm. Find the radius of the circle.
Solution. Let PQ be a tangent to the circle from point P and OQ be the radius at the point of contact.   

Question. A circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ = 1/2 (Perimeter of ΔABC).
Solution. Since tangents from an exterior point to a circle are equal in length. 
∴ BP = BQ …(i)
CP = CR …(ii)
and, AQ = AR …(iii)
from eqn. (iii), we have AQ = AR
⇒ AB + BQ = AC + CR
⇒ AB + BP = AC + CP …(iv)
[∴ using (i) and (ii)]

Now, Perimeter of ΔABC = AB + BC + AC
= AB + (BP + PC) + AC
= (AB + BP) + (AC + PC)
= 2 (AB + BP) [using (iv)]
= 2 AQ [using (i)]
AQ = 1/2 (Perimeter of ΔABC).

Assignments for Class 10 Mathematics Circles as per CBSE NCERT pattern

All students studying in Grade 10 Mathematics Circles should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Circles exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Circles which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.

Some advantages of Free Assignments for Class 10 Mathematics Circles

1. Solving Assignments for Mathematics Circles Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
2. By solving one assignments given in your class by Mathematics Circles teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
3. You will be able to understand the type of questions which are expected in your Mathematics Circles class test
4. You will be able to revise all topics given in the ebook for Class 10 Mathematics Circles as all questions have been provided in the question banks
5. NCERT Class 10 Mathematics Circles Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
6. Parents will be able to take print out of the assignments and give to their child easily.

All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Circles teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Circles Assignments PDF.