Assignments for Class 10 Mathematics Construction have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Construction from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Construction. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Construction book and get good marks in class 10 exams.
Construction
To divide a line segment in a given ratio.(lets say m:n).
Let AB line has to divide in 3:2 ratio. Here m=3 and n=2.
- Draw a ray AX making acute angle with AB.
- Locate m + n point on AX such that for all points.
- Join BAm + n .
- Draw a line A3C from A3 to AB which is parallel to BX.
- AC and CB are the desired ratio (here 3:2) in which line has to be divided.
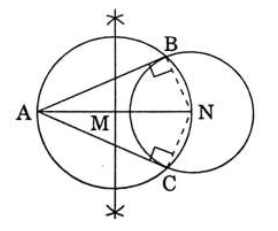
To construct the pair of tangents from an external point to a circle.
If we have to draw a tangent from point A to a given circle of center O, then.
- Draw a line AN.
- Bisect this line AN. Midpoint on line is M.
- With AN as diameter, draw a circle with center M.
- Join A with the points B and C where this circle cuts the given circle.
- AB and AC are the required two tangents.
To construct a triangle similar to a given triangle as per a given scale factor.
Scale factor less than one. (Triangle will be smaller than the given triangle).
Scale factor greater than one (Triangle will be greater than the given triangle).
- Draw a ray BX making an acute angle with BC on the side opposite to the vertex A.
- When scale factor is less than one : locate denominator it is greater number of fraction. For example in scale we 3/4, have to locate 4).
- When scale factor is greater then one : locate numerator it is greater number of fraction. For example in scale 5/4, have to locate 5.
- Point B1,B2,B3,B4 Bon BX so that BB1 =B1B2 =B2B3 =B3B4=B4B5 .
- When scale factor is less than one : Join B4C and draw a line through B3 (the 3rd point, 3 being smaller number in fraction ¾) Parallel B4C to intersect BC at C’.
- Draw a line through C’ parallel to the line CA to intersect BA at A’ then,Δ A’B C’ is the required triangle.
- When scale factor is greater than one : Join B4C (the 4th point, 4 being smaller number in fraction 5/4).
- Draw a line through B5 (the 5th point, 5th being greater number in fraction 5/4) parallel to the line B4C to intersect BC externally at C” ., Δ A”B C” Then, is the required triangle.

Question. Construct a triangle similar to a given triangle with sides 7 cm, 9 cm and 10 cm and whose sides are 5/7 th of the corresponding sides of the given triangle.
Solution. Steps of Constructions :
1. With the given measurements construct the triangle ABC in which AB = 7 cm, BC = 9 cm and AC = 10 cm
2. Draw a ray AP, making any suitable angle with AB and on opposite side of vertex C.

3. Starting from A, cut off seven equal line-segments AX1, X1X2, X2X3, X3X4, X4X5, X5X6 and X6X7 on AP.
4. Join BX7 and draw a line X5B’ parallel to X7B which meets AB at B’.
5. Through B’, draw B’C’ || BC which meets AC at point C’.
The ΔAB’C’, so obtained, is similar to the given ΔABC and each side of ΔAB’C’ is 5/7 times the corresponding side of ΔABC.
Question. Draw a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.
Solution. Step of Constructions :
1. Draw a circle with centre O and radius = 3 cm

2. Draw any radius OA.
3. Draw another radius OB such that ∠AOB = 180° – 60° = 120°.
4. At point A, draw AM ⊥ OA i.e. draw tangent AM.
5. At B, draw tangent BN to the given circle.
6. The two tangents meet at point P in such a way that ∠APB = 60°.
∴ PA and PB are the required tangents.
Question. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm.
Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Solution. Step of Constructions :
1. Draw BC = 4 cm
2. At B, draw a ray BP making angle 90° with BC i.e. ∠PBC = 90°
3. From BP, cut BA = 3 cm
4. Join A and C to get the given ΔABC.
5. Through vertex B, draw ray BX making any suitable angle with BC.
6. On BX cut 5 equal line segments BB1 = B1B2 = B2B3 = B3B4 = B4B5.

7. Join B3 to C.
8. Through B5, draw a line parallel to B3C to meet BC produced at point C’.
9. Through C’, draw a line parallel to side CA to meet BA produced to A’. A’BC’ is the required triangle.
Question. Draw a line segment of length 7 cm and divide it in the ratio 2 : 3.
Solution. Step of constructions :
1. Draw AB = 7 cm
2. Draw ray AX making a suitable acute angle with AB.
3. Cut 2 + 3 = 5 equal segments AA1, A1A2, A2A3, A3A4 and A4A5 on AX.
4. Join A5 with B.5. Through A2, draw A2P parallel to A5B by making corresponding angles AA2P and AA5B equal.
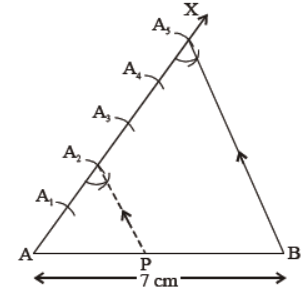
6. The line through A2 and parallel to A5B will meet the given line segment at point P.
Then P is the required point which divides AB in the ratio 2 : 3 i.e. AP : PB = 2 : 3
Proof :
Since in a triangle the line drawn parallel to one side of the triangle divides other two sides
proportionally, ∴ In ΔAA5B, A2 P || A5B
⇒ AP/PB = AA2/A2A5 i.e. AP/PB = 2/3
Question. Draw a line segment of length 7.8 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution. Steps:
(i) Draw a line segment AB = 7.8 cm.
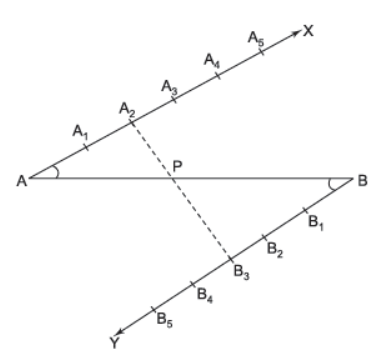
(ii) Draw ray AX making any suitable angle with AB.
(iii) Draw ray BY parallel to ray AX by making alternate angles BAX and ABY equal.
(iv) Since 5 + 8 = 13, from AX cut 13 equal segments i.e., AA1, A1A2, A2A3, …, A12A13.
(v) Also, from BY cut 13 equal segments [of the same size as taken in step (iv)] i.e., BB1, B1B2, B2B3, …, B12B13.
(vi) Join A5 with B8.
Line joining A5 and B8 cuts line segment AB at point P.
∴ P is the required point such that AP : PB = 5 : 8.
On measuring we find: AP = 3 cm and BP = 4.8 cm.
Question. In the figure given on the next page, if B1, B2, B3,…… and A1, A2, A3,….. have been marked at equal distances. In what ratio C divides AB?

Solution. 8 : 5 (1)
Question. To divide a line segment BC internally in the ratio 3 : 5, we draw a ray BX such that ∠CBX is an acute angle. What will be the minimum number of points to be located at equal distances, on ray BX?
Solution. 8
Question. Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that AP : PB = 3 : 5.
Solution. Steps of construction:
(i) Draw a line segment AB = 7 cm.
(ii) Draw AX || BY such that ∠A and ∠B are acute angles.
(iii) Divide AX and BY in 3 and 5 parts equally by
compass and mark A1, A2, A3, B1, B2, B3, B4 and B5 respectively.
(iv) Join A3B5 which intersects AB at P and divides AP :
PB = 3 : 5.
Hence, P is the required point on AB which divides it in 3 : 5.
Question. Draw a line segment of length 6 cm. Using compasses and ruler, find a point P on it which divides it in the ratio 3 : 4.
Solution. Steps of construction:
(i) Draw a line segment AB = 6 cm.
(ii) Draw any ray AX making an acute angle XAB with AB.
(iii) Along AX mark 7 (3 + 4) points A1, A2, A3, A4,
……, A7 at equal distances such that AA1 = A1A2
= ….. = A6A7.
(iv) Join A7B.
(v) From A3, draw A3P parallel to A7B (by making an angle equal to ∠AA7B at A3), to meet AB at point P.
Then AP : PB = 3 : 4.
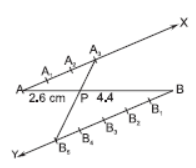
Question. Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution. Steps of construction:
(i) Draw a line segment AB = 7.6 cm.
(ii) Draw a ray AX making an acute angle with AB.
(iii) Mark 13 (8 + 5) equal points on AX, and mark them
as X1, X2, X3, …….., X13.
(iv) Join ‘point X13’ and B.
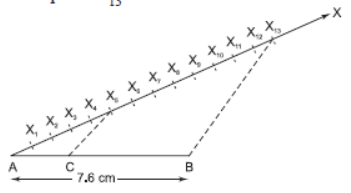
(v) From ‘point X5’, draw X5C || X13B, which meets AB at C.
Thus, C divides AB in the ratio 5 : 8
On measuring the two parts, we get:
AC = 2.9 cm and BC = 4.7 cm.
Question. ABC be a right triangle in which AB = 6 cm, BC = 4 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution. Steps:
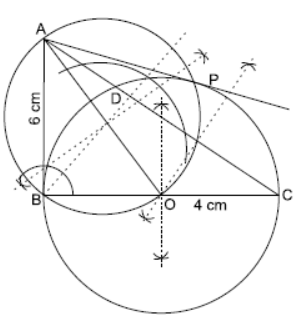
(i) Draw perpendicular bisectors of BC and CD which meet at point O.
O is the centre of the circle through B, C and D.
(ii) Join A and O.
(iii) Draw a circle with AO as diameter which meets the given circle at points P and B.
(iv) Join AP and AB.
AP and AB are the required tangents.
Question. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure its length.
Solution. Steps:
(i) With point O as centre, draw a circle of radius = 6 cm.
(ii) Mark a point A such that OA = 10 cm.
(iii) Join O and A. Then, draw the perpendicular bisector of OA which cuts OA at point B.
(iv) With B as centre and AB = BO as radius, draw a circle which cuts the circle drawn in step (i) at points P and Q.
(v) Join PA and QA.
PA and QA are the required tangents.
On measuring, we find PA = QA = 8 cm.
Question. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Solution. Steps:
(i) Mark a point as O.
(ii) With O as centre, draw two circles with radii 4 cm and 6 cm respectively.
(iii) On the bigger circle, mark a point A.
(iv) Join O and A.
(v) Draw perpendicular bisector of OA to get its mid-point P.
(vi) With P as centre and PA = PO as radius, draw a semicircle which meets smaller circle at point B.
(vii) Join A and B, and produce it to meet outer circle at point C. ABC is the required tangent.
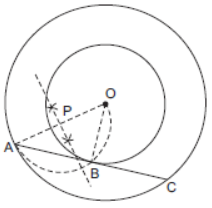
The length of AB = 4.5 cm (approx.)
Verification: Join OB.
Since, angle between radius and tangent is 90°.
⇒ ∠ABO = 90°.
In right ΔABO, AB2 + OB2 = OA2
⇒ AB2 = 62 – 42 = 36 – 16 = 20
and AB = √20 cm = 4.5 cm (approx.)
Question. Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle.
Solution. Steps of construction:
(i) Draw a right angle triangle ABC, right angled at B,
AB = 6 cm and BC = 8 cm.
(ii) Draw BD ⊥ AC.
(iii) Draw a circumcircle of DBDC.
(iv) From point A draw a pair of tangents AB and AP.
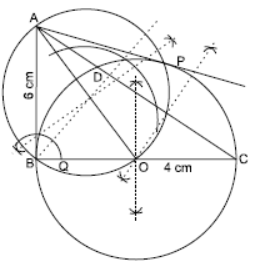
Then AB and AP are the required tangents.
Question. Draw two concentric circles C1 and C2 of radii 3 cm and 5 cm. Taking a point on outer circle C2, construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Solution. 4 cm
Question. Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
Solution. Steps of construction:
(i) Take point O. Draw two concentric circles of radii 3 cm and 5 cm respectively.
(ii) Locate point P on the circumference of larger circle.
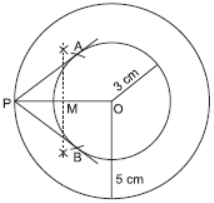
(iii) Join OP and bisect it. Let M be mid-point of OP.
(iv) Taking M as centre and MP as radius, draw an arc intersecting smaller circle at A and B.
(v) Join PA and PB. Thus, PA and PB are required tangents.
Question. Is it possible to construct a pair of tangents from point P to circle of radius 5 cm situated at a distance of 4.9 cm from the centre?
Solution. No
Question. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution. Steps of construction:
(i) A circle, with centre O and radius 5 cm is drawn.
(ii) As tangents are inclined at 60°.
∴ ∠TOS = 120°.
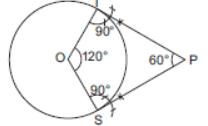
(iii) Two radius OT and OS, inclined at an angle of 120° are drawn.
(iv) Tangents are drawn to the circle at T and S meeting at P.
Then PT and PS are the required tangents.
Question. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameters each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution. Steps of construction:
(i) Join P and O.
(ii) Bisect PO such that M be its mid-point.
(iii) Taking M as centre and MO as radius, draw a circle.
Let it intersects the given circle at A and B.
(iv) Join PA and PB.
Thus, PA and PB are the two required tangents from P.
(v) Now, join O and Q.
(vi) Bisect OQ such that N is its mid-point.
(vii) Taking N as centre and NO as radius, draw a circle.
Let it intersects the given circle at C and D.
(viii) Join QC and QD.

Thus, QC and QD are the required tangents to the given circle.
Question. Is it possible to construct a pair of tangents from point P lying on circle of radius 4 cm and centre O?
Solution. No
Question. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution. Steps of construction:
(i) AB = 8 cm is taken.
(ii) With centre A, a circle of radius 4 cm is drawn and with centre B, a circle of radius 3 cm is drawn.
(iii) With AB as diameter, a circle is drawn meeting circle with centre A at S and T respectively and circle with centre B at P and Q respectively.
(iv) Then AP and AQ are tangents from A to circle with centre B and BS and BT are tangents from B to circle with centre A.
Question. Draw a circle of radius 3 cm. From a point 6 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution. 5.20 m (approx)
Assignments for Class 10 Mathematics Construction as per CBSE NCERT pattern
All students studying in Grade 10 Mathematics Construction should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Construction exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Construction which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.
Some advantages of Free Assignments for Class 10 Mathematics Construction
- Solving Assignments for Mathematics Construction Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
- By solving one assignment given in your class by Mathematics Construction teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
- You will be able to understand the type of questions which are expected in your Mathematics Construction class test
- You will be able to revise all topics given in the ebook for Class 10 Mathematics Construction as all questions have been provided in the question banks
- NCERT Class 10 Mathematics Construction Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
- Parents will be able to take print out of the assignments and give to their child easily.
All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Construction teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Construction Assignments PDF.

You can download free assignments for class 10 Mathematics Construction from https://www.assignmentsbag.com
You can get free PDF downloadable assignments for Grade 10 Mathematics Construction from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided assignments for all subjects in Grade 10, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge
Yes all test papers for Mathematics Construction Class 10 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.
https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.


