Assignments For Class 10 Mathematics Arithmetic Progression

Assignments for Class 10 Mathematics Arithmetic Progression have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Arithmetic Progression from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Arithmetic Progression. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Arithmetic Progression book and get good marks in class 10 exams.

Question. In an Arithmetic progression, the 4th term is 11 and the 12th term is 35, then the first term of the series is 
(A) 5 
(B) 4
(C) 3
(D) 2

Question. If the sum of 16 terms of an AP is 1624 and the first term is 500 times the common difference, then find the common difference.       
(A) 5
(B) 1/2
(C) 1/5
(D) 2

Question. Divide 32 into four parts which are in A.P. such that the ratio of product of extremes to the product of means is 7:15   
(A) 1,5,9,13
(B) 3,7,11,15
(C) 2,6,10,14
(D) 4,8,12,16

Question. If the sum of series 2,5,8,11……………… is 60100, find n?   
(A) 200
(B) 210
(C) 220
(D) 240

Question. The first and last term of an A.P. are a and l respectively. If S is the sum of all the terms of the A.P, and the common difference is given by l2 -a2 /k -(l-a) then k=       
(A) S
(B) 2S
(C) 3S
(D) none of these

Question. The first term of the A.P whose third term is 16 and the difference of 5th and 7th term is 12 is   
(A) 7
(B) 6
(C) 5
(D) 4

Question. If a,b,c,d,e are in A.P. find the value of a -4b+6c -4d +e ?   
(A) 0
(B) 1
(C) 2
(D) 3

Question. If the sides of right angled triangle are in A.P., then the sines of acute angles are?   
(A) 3/5, 4/5
(B) 1/√3 ,√(2/3)
(C) 1/2 ,√3/2
(D) 1/√2, √3/2

Question. Concentric circles of radii 1,2,3,……..100 cm are drawn. The interior of the smallest circle is coloured red and the angular regions are colored alternatively green & red, so that no two adjacent regions are of same coloured find total area of green regions in sq. cm.?   
(A) 1000π
(B) 5050π
(C) 4950π
(D) 5151π

Question. In a certain A.P., 5 times the 5th term is equal to 8 times the 8th term find the 13th term?   
(A) 5
(B) 2
(C) 0
(D) 1

Question. Two arithmetic progressions have equal common differences. The first term of one of these is 3 and that of the other is 8, then the difference between their 100th terms is 
(A) 4
(B) 5
(C) 6
(D) 3

Question. If a, b and c are in arithmetic progression, then b + c, c + a and a + b are in   
(A) arithmetic progression
(B) geometric progression
(C) harmonic progression
(D) none of these

Question. Given two A.P.’s 2,5,8,11………………T60 and 3,5,7,9……………..T50. Find the number of terms which are identical?   
(A) 17
(B) 18
(C) 19
(D) 20

Question. If pth, qth, rth terms of an A.P. are a,b,c, respectively. Find the value of a(q-r) + b (r-p) +c(p-q)
(A) 2
(B) 1
(C) 0
(D) 5

Question. Let Sn denote the sum of n terms of an A.P. whose first term is a. If the common difference d is given by d =S_n -kS_n-2 , then k=     
(A) 1
(B) 2
(C) 3
(D) none of these

Question. If the sum of three numbers in A.P. is 24 and their product is 440. Find the numbers?   
(A) 5,8,11
(B) 5,9,11
(C) 2,4,9
(D) 2,6,9

Question. If 3 positive real nos, a,b,c, are in A.P. such that abc=4, find minimum value of b?   
(A) 2^1/3 
(B) 2^1/2
(C) 2^2/3
(D) 2^3/2

Question. In an AP, the sum of first n term is (3n2/2 + 5n/2 ).Find its 25th term. 
(A) 66
(B) 86
(C) 76
(D) 96

Question. If the 12th term of an A.P. is -13 and the sum of the first four terms is 24 what is the sum of the first 10 terms. 
(A) 150
(B) -1
(C) 180
(D) zero

Question. An AP starts which a positive fraction and every alternate term is an integer. If the sum of the first 11 terms is 33, then find the fourth term.   
(A) 2
(B) 3
(C) 5
(D) 6 

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set A

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set B

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set C

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set D

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set E

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set F

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set G

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set H

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set I

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set J

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set K

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set L

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set M

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set N

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set O

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set P

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set Q

CBSE Class 10 Mathematics Arithmetic Progression Assignment Set R

CBSE Class 10 Mathematics Arithmetic Progression Assignments Set A

CBSE Class 10 Mathematics Arithmetic Progression Assignments Set B

CBSE Class 10 Mathematics Arithmetic Progression Assignments Set C

CBSE Class 10 Mathematics Arithmetic Progression Assignments Set D

Short Answer type Questions :

Question. If the sum of the first q terms of an AP is 2q + 3q², what is its common difference? 
Solution. Given that,
S_q = 2q + 3q²
S₁ = 2 + 3 = 5 = T1 = First term [put q = 1]
S₂ = 4 + 3(4) = 16 [put q = 2]
S₃ = 6 + 3(9) = 33 [put q = 3](½)
∴ 2nd term,
T₂ = S₂ – S₁ = 16 – 5 = 11
∴ 3rd term,
T₃ = S₃ – S₂ = 33 – 16 = 17
Common difference
= T₃ – T₂ = 17 – 11 = 6

Question. If n^th term of an AP is (2n + 1), what is the sum of its first three terms? 
Solution. a₁ = 3, a₃ = 7, S₃ = 3/2 (3 + 7) = 15 [½+½]

Question. Find the sum of first 100 natural numbers.
Solution. Natural numbers are 1, 2, 3, 4, …
The sum of first 100 natural numbers is given by
S_n = n(n + 1)/2 = 100 x (100 + 1)/2
= 100 x 101 /2
= 50 × 101 = 5050

Question. In an AP, the first term is –4, the last term is 29 and the sum of all its terms is 150. Find its common difference.
Solution. 150 = n/2 (−4 + 29) ∴ Sn = n/2 (a + 1)
⇒ 300 = 25n fi n = 12 (1)
∴ Then, l = a12 = 29 = –4 + 11d
⇒ 11d = 33 ⇒ d = 3

Question. Find the sum of all three digit natural numbers, which are multiples of 11. 
Solution. 3-digit natural numbers which are multiples of 11 are 110,
121, 132, …, 990
nth term, 990 = 110 + (n – 1)11
⇒ n = 81 (1)
∴ Sum of ‘n’ terms,
S_n = n/2 [a +l]
= 81/2 [110 + 990] = 44550
∴ Sum of all three-digit natural numbers, which are multiples of 11 is 44550.

Question. How many terms of the AP: 18, 16, 14, … be taken so that their sum is zero? 
Solution. Let the number of terms taken for sum to be zero be n.
Then, sum of n terms
(Sn) = 0
⇒ Sn = n/2 [2a +(n – 1)
⇒ 0 = n/2 [2 ×18 + ( −1)(−2)]
⇒ n = 19
Hence, sum of 19 terms is 0.

Question. The first and the last term of an AP are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum? 
Solution. 39; 6981

Question. The ratio of the 11th term to the 18th term of an AP is 2 : 3. Find the ratio of the 5th term to the 21st term, and also the ratio of the sum of the first five terms to the sum of the first 21 terms. 
Solution. 1 : 3, 5 : 49

Question. Find the sum of first n terms of an AP whose nth term is 5n – 1. Hence find the sum of first 20 terms. 
Solution. Given: an = 5n – 1  
a₁ = 4
∴ a₂ = 5(2) – 1 = 9
d = a₂ – a₁ = 9 – 4 = 5 
Now, sum of first ‘n’ terms,

Question. The sum of the first five terms of an AP is 55 and sum of the first ten terms of this AP is 235, find the sum of its first 20 terms.
Solution. 970

Question. In an AP, if S₅ + S₇ = 167 and S₁₀ = 235, then find the AP, where Sn denotes the sum of its first n terms. 
Solution. S₅ + S₇ = 167 

Question. The sum of first n terms of an AP is given by S_n = 2n² + 3n. Find the sixteenth term of the AP.
Solution. Sn = 2n² + 3n
S₁ = 5 = a₁
S₂ = a1 + a₂ = 14 ⇒ a₂ = 9 
d = a₂ – a₁ = 4
a₁₆ = a₁ + 15d = 5 + 15(4) = 65

Question. How many multiples of 4 lie between 10 and 250? Also find their sum.
Solution. 60, 7800

Question. How many terms of the AP: 24, 21, 18, … must be taken so that their sum is 78?
Solution. AP is 24, 21, 18, …
Here, a = 24 and d = 21 – 24 = 18 – 21 = –3
Let the sum of n terms of the AP be 78.
S_n = n/2 [2a + (n – 1)d]
⇒ 78 = n/2 [2 × 24 + (n – 1)(–3)]
⇒ 78 × 2 = n[48 – 3n + 1]
⇒ 156 = n(49 – 3n)
⇒ 156 = 49n – 3n2
⇒ 3n² – 49n + 156 = 0 
We know that         37

Question. The sum of first six terms of an AP is 42. The ratio of its 10th term to its 30th term is 1 : 3. Calculate the first and the thirteenth terms of the AP. 
Solution. 2 and 26

Question. Find the sum of all multiples of 7 lying between 500 and 900. 
Solution. 39, 900

Question. In an AP, if the 6th and 13th terms are 35 and 70 respectively, find the sum of its first 20 terms.   
Solution. Given that, a₆ = 35 fi a + 5d = 35 …(i)
and also a₁₃ = 70 fi a + 12d = 70 …(ii)(1)
On solving the above equations, we get
a = 10; d = 5 
Now, sum of first 20 terms,

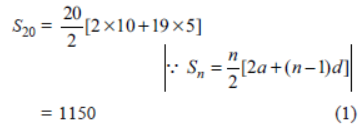
Question. Find the sum of first 10 terms of the AP: 2, 7, 12, … 
Solution. 245

Question. If the sum of first m terms of an AP is 2 m² + 3 m, then what is its second term? 
Solution. 9

Question. The sum of the 2nd and the 7th terms of an AP is 30. If its 15th term is 1 less than twice its 8th term, find the AP. 
Solution. Given, a₂ + a₇ = 30
⇒ a + d + a + 6d = 30
⇒ 2a + 7d = 30 …(i)(1)
[∴ an = a + (n – 1)d]
Also, given a₁₅ = 2a8 – 1
⇒ a + 14d = 2(a + 7d) – 1 fi a = 1 (1)
Putting the value of a in (i), we get
2 + 7d = 30 fi d = 4
∴ a = 1, d = 4
Hence, AP is 1, 5, 9, 13, 17, …

Question. Find the middle term of the sequence formed by all three-digit numbers which leave a remainder 3, when divided by 4. Also, find the sum of all numbers on both sides of the middle terms separately. 
Solution. List of 3-digit number leaving remainder 3 when divided
by 4, are 103, 107, 111, …, 999.
Now, an = 999 fi a + (n – 1)d = 999
103 + (n – 1)4 = 999 fi n = 225 
Since, number of terms is odd, so there will be only one middle term     

Question. If the ratio of the sum of first n terms of two AP’s is (7n + 1) : (4n + 27), find the ratio of their mth terms.   
Solution. Let Sn and Sn’ be the sum of n terms of two APs. Let a, a¢ and d, d¢ be first terms and common differences of two APs. Then  20

Question. Find the sum of first 8 multiples of 3.
Solution. S₈ = 3 + 6 + 9 + 12 +….+ 24
= 3(1 + 2 + 3 + …+ 8)
= 3 × 8 x 9/2 = 108

Question. If the sum of first 14 terms of an AP is 1050 and its first term is 10, find the 20th term.
Solution. Let common difference be d.   

Question. Find the number of terms of the AP: 54, 51, 48, … so that their sum is 513. 
Solution. 18 or 19

Question. The digits of a positive number of three digits are in AP and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number.  
Solution. Let the required numbers in AP are a – d, a, a + d
respectively.
Now, a – d + a + a + d = 15 [∴ Sum of digits = 15]
⇒ 3a = 15 fi a = 5 (1)
According to question, number is
100(a – d) + 10a + a + d, i.e. 111a – 99d
Number on reversing the digits is
100(a + d) + 10a + a – d, i.e. 111a + 99d
Now, as per given condition in question,
(111a – 99d) – (111a + 99d) = 594 (1)
⇒ d = –3
∴ Digits of number are [5 – (–3), 5, (5 + (–3))]
= 8, 5, 2.
∴ Required number is 111 × (5) – 99(–3)
= 555 + 297 = 852.

Question. Find the sum of n terms of the series (4 – 1/n) + (4 – 2/n) + (4 – 3/n) + ……….
Solution.    

Question. The first term of an AP is 5, the last term is 45 and sum is 400. Find the number of terms and the common difference.
Solution. a = 5
a_n = 45
S_n = 400
⇒ n/2 (5 + 45) = 400
50n = 800 (1)
n = 16
also an = 45
5 + 15d = 45
15d = 40
d = 8/3

Question. Solve the equation: 1 + 4 + 7 + 10 + … + x = 287.   
Solution. Given equation: 1 + 4 + 7 + 10 + … + x = 287
Here, a = 1, d = 4 – 1 = 7 – 4 = 3
S_n = 287

Question. If the ratio of the sum of the first n terms of two APs is (7n + 1) : (4n + 27), then find the ratio of their 9^th terms.
Solution. Let the first terms be a and a′ and d and d′ be their respective common differences. 

Question. The sum of the first three numbers in an arithmetic progression is 18. If the product of the first and the third terms is 5 times the common difference, find the three numbers.  
Solution. Let the three numbers in AP are a – d, a, a + d
Then a – b + a + a + d = 18
⇒ 3a = 18 ⇒ a = 6 (1)
Given: (a – d) (a + d) = 5d
⇒ a² – d² = 5d ⇒ a² = 5d + d²
⇒ 36 = 5d + d2 [Q a = 6](1)
⇒ d² + 5d – 36 = 0
⇒ d² + 9d – 4d – 36 = 0 
⇒ d(d + 9) – 4(d + 9) = 0
⇒ (d – 4) (d + 9) = 0
⇒ d – 4 = 0 or d + 9 = 0
⇒ d = 4 or d = –9 
⇒ d = 4 (1)
Thus, three numbers are a – d, a, a + d
= 6 – 4, 6, 6 + 4
= 2, 6, 10

Question. Find the sum of first 10 multiples of 6. 
Solution. First 10 multiples of 6 are 6, 12, 18, ….., 60.
This is an AP in which a = 6, n = 10 and d = 6.
∴ Sum of first 10 multiples of 6 = S10
⇒ S10 = n/2 [2a + (n – 1)d]
=10/2 [2×6 +(10 – 1) 6]
= 5 (12 + 54)
= 5 × 66 = 330

Question. The first and the last terms of an AP are 8 and 65 respectively. If sum of all its terms is 730, find its common difference.
Solution.    

Question. The sum of the first n terms of an AP is 4n² + 2n. Find the nth term of this AP. 
Solution. Given, S_n = 4n² + 2n
So, S_n – 1 = 4(n – 1)2 + 2(n – 1)
= 4(n² – 2n + 1) + 2n – 2
= 4n² – 8n + 4 + 2n – 2
= 4n² – 6n + 2 (1)
an = Sn – Sn – 1 = nth term
= (4n² + 2n) – (4n² – 6n + 2)
= 4n² + 2n – 4n² + 6n – 2
= 8n – 2

Question. What is the sum of five positive integers divisible by 6? 
Solution. 90

Question. If m times the mth term of an arithmetic progression is equal to n times its nth term and m ≠ n, show that the (m + n)th term of the AP is zero.
Solution. We know that an = a + (n – 1)d
From the given conditions,
m[a + (m – 1) d] = n[a + (n – 1)d]
⇒ m[a + (md – d)] = n[a + nd – d] 
⇒ am + m²d – md = an+ n²d – nd
⇒ am – an + m²d – n²d – md + nd = 0 
⇒ a(m – n) + d(m² – n²) – d(m – n) = 0
⇒ a(m – n) + (m + n) (m – n)d – (m – n)d = 0 
⇒ (m – n) [a + (m + n)d – d = 0
⇒ a + md + nd – d = 0 (1)
⇒ a + (m + n – 1)d = 0
Since, m ≠ n, it is clear that (m + n)th term of the AP is zero.

Question. The sums of n terms of two APs are in the ratio 5n + 4 : 9n + 6. Find the ratio of their 25th terms. 
Solution. 249 : 447

Question. Find a, b, and c such that the numbers a, 7, b, 23, c are in AP. 
Solution. a = –1, b = 15, c = 31

Question. For what value of k will k + 9, 2k – 1 and 2k + 7 are the consecutive terms of an AP?
Solution. Given that k + 9, 2k – 1 and 2k + 7 are in AP
Then,
(2k – 1) – (k + 9) = (2k + 7) – (2k – 1)
⇒ k – 10 = 8
⇒ k = 18

Question. Find the value of x so that –6, x, 8 are in AP.
Solution. 1

Question. For what value of k will the consecutive terms 2k + 1, 3k + 3 and 5k – 1 form an AP? 
Solution. Given that 2k + 1, 3k + 3 and 5k – 1 are in AP.
So, (3k + 3) – (2k + 1) = (5k – 1) – (3k + 3)
⇒ k + 2 = 2k – 4
⇒ 2k – k = 2 + 4
⇒ k = 6

Question. Find the eleventh term from the last term of the AP: 27, 23, 19, …, –65. 
Solution. a₁₁ = –25

Question. The nth term of an AP is (7 – 4n), then what is its common difference?
Solution. an = 7 – 4n
⇒ a1 = 7 – 4 × 1 = 3
⇒ a2 = 7 – 4 × 2 = 7 – 8 = –1
a3 = 7 – 4 × 3 = 7 – 12 = –5
Now, a₂ – a1 = –1 – 3 = –4
a3 – a₂ = –5 – (–1)
= –5 + 1 = –4
So, the common difference of AP is –4.

Question. Write first four terms of the AP, whose first term and the common difference are given as follows:
a = 10, d = 10
Solution. 10, 20, 30, 40

Question. Find the 10th term of the AP: 2, 7, 12, … 
Solution. 47

Question. In the given AP, find the missing terms: ……., 13, ……., 3.
Solution. 18, 8

Question. Find the 6th term from the end of the AP: 17, 14, 11, …, –40.
Solution. –25

Question. Which term of the AP: 21, 18, 15, … is zero? 
Solution. 8

Question. Find the 11^th term of the AP: –27, –22, –17, –12, … .
Solution. 23

Question. Write the next term of the AP: √8, √18, √32 , ……….. 
Solution. √50 or 5 √2

Question. Find the common difference of the AP whose first term is 12 and fifth term is 0.
Solution. A5 = a1 + 4d = 0
12 + 4d = 0
d = –3

Question. Find how many integers between 200 and 500 are divisible by 8.
Solution. AP formed is 208, 216, 224, …., 496
an = 496 (1)
⇒ 208 + (n – 1) × 8 = 496
⇒ n = 37

Question. Find the middle term of the AP: 6, 13, 20, …, 216. 
Solution. Given AP is 6, 13, 20, …, 216
nth term, an = 216
⇒ a + (n – 1)d = 216
⇒ 6 + 7(n – 1) = 216
⇒ 7n = 217
⇒ n = 31 (1)
Since, the number of terms in AP are 31, so, the middle most term is 16^th term. 

Question. The nth term of an AP is 6n + 2. Find its common difference. 
Solution. 6

Question. Which term of the progression 20 19 , 1/4 , 18,1/2 , 17,3/4 ,… is the first negative term?
Solution. Here d = -3/4
Let the nth term be first negative term.
∴ 20 + (n -1) (-3/4) < 0 ⇒ 3n > 83
⇒ n > 27, 2/3
Hence, 28^th term is first negative term.

Question. How many two-digit numbers are divisible by 7? 
Solution. Two-digit numbers which are divisible by 7 are 14, 21, 28, …, 98.
Let an = 98
⇒ a + (n – 1)d = 98 (1)
⇒ 14 + 7(n – 1) = 98
n = 13
Hence, there are 13 two-digit numbers which are divisible by 7.

Question. Which term of the AP: 3, 14, 25, 36, … will be 99 more than its 25th term? 
Solution. Let an be the term which is 99 more than 25th term of given
AP.
ATQ, an = a25 + 99
⇒ a + (n – 1)d = a + 24d + 99
⇒ 11(n – 1) = 24 × 11 + 99
⇒ n = 34
Hence, 34^th is the required term.

Question. In an AP, the first term is 12 and the common difference is 6. If the last term of the AP is 252, find its middle term.
Solution. Let an = 252 = last term
⇒ a + (n – 1)d = 252
⇒ 12 + (n – 1)6 = 252
⇒ n = 41 (1)
∴ Since number of terms is odd, so only one middle term.
Now, middle term = (41 + 1/2)
= 21st term
∴ 21st term, a₂₁ = a + 20d
= 12 + 20 × 6
= 132
= middle term value.

Question. Which term of the AP: 3, 15, 27, 39, … will be 120 more than its 21st term? 
Solution. AP: 3, 15, 27, 39, …
a = 3, d = 15 – 3 = 12
a₂₁ = a + 20d = 3 + 20 × 12
= 3 + 240 = 243
120 more than a₂₁ = 243 + 120 = 363 
Let 363 be nth term.
So, 363 = 3 + (n – 1) 12
⇒ 360 = 12(n – 1)
30 = n – 1 ⇒ n = 31
Thus, 31st term of the given AP is 120 more than its 21^st term.

Question. If the first three terms of an AP are b, c and 2b, then find the ratio of b and c. 
Solution. b, c and 2b are in AP
⇒ c = 3b/2
∴ b : c = 2 : 3

Question. The pth, qth and rth terms of an AP are a, b and c respectively. Show that a(q – r) + b(r – p) + c(p – q) = 0.
Solution. Let A and d be the first term and common difference of
the given AP, then
ap = A + (p – 1)d = a …(i)
aq = A + (q – 1)d = b …(ii)
ar = A + (r – 1)d = c …(iii)
Now, subtracting (i) and (ii), we get
(p – q)d = a – b 

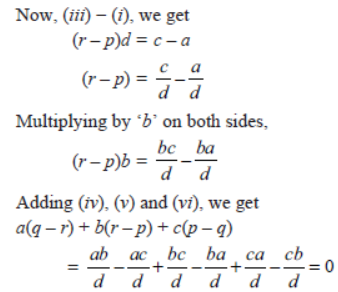
Question. Determine k so that k² + 4k + 8, 2k² + 3k + 6, 3k² + 4k + 4 are three consecutive terms of an AP. 
Solution. k = 0

Question. If the nth terms of two APs: 23, 25, 27, … and 5, 8, 11, 14, … are equal, then find the value of n.
Solution. AP₁ = 23, 25, 27, …
Here, a₁ = 23
d₁ = 25 – 23 = 27 – 25 = 2
∴ n^th term = a1 + (n – 1)d1
= 23 + (n – 1)2
AP₂ = 5, 8, 11, 14, … (1)
Here, a² = 5
d₂ = 8 – 5 = 11 – 8 = 3
∴ nth term = a₂ + (n – 1)d₂
= 5 + (n – 1)3 (1)
Now, 23 + (n – 1)2 = 5 + (n – 1)3
⇒ 23 + 2n – 2 = 5 + 3n – 3
⇒ 3n – 2n = 23 – 2 – 5 + 3
⇒ n = 26 – 7 = 19

Question. How many natural numbers are there between 200 and 500, which are divisible by 7?
Solution. Natural numbers between 200 and 500 which are divisible
by 7 are as 203, 210, 217, …, 497
Let above are n numbers and an = 497
a + (n – 1)d = 497 (1)
⇒ 203 + 7(n – 1) = 497
⇒ n = 43
∴ There are 43 natural numbers between 200 and 500
divisible by 7.

Question. The 19^th term of an AP is equal to three times its sixth term. If its 9^th term is 19, find the AP.
Solution. 3, 5, 7, 9, …

Question. Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5. 
Solution. Numbers between 101 and 999 which are divisible by both
2 and 5 (i.e., by 10) are 110, 120, 130, … 990.
Now, an = a + (n – 1)d (1)
⇒ 990 = 110 + (n – 1)10
⇒ n = 89
∴ Natural numbers which are divisible by 2 and 5 both are 89.

Question. How many two digits numbers are divisible by 3?
Solution. 2-digit numbers divisible by 3 are 12, 15, 18, …, 99 which is in AP.
So, an = 99, d = 15 – 12 = 3
Now, an = a + (n – 1) d (1)
⇒ 99 = 12 + (n – 1) 3
⇒ 87 = 3 (n – 1)
⇒ 29 = n – 1
⇒ n = 30
Thus, 30, 2-digit numbers are divisible by 3

Question. Find the 9^th term from the end (towards the first term) of the AP: 5, 9, 13, …, 185. 
Solution. Reversing the given AP, we get
185, 181, 174, …, 9, 5
Ninth term a9 = a + (9 – 1)d
= 185 + 8 × (– 4)
= 185 – 32
= 153

Question. If 1/x + 2 , 1/ x + 3 and 1/ x + 5 are in AP, find the value of x.
Solution. Given term are in AP   

Question. Is –150 a term of the AP: 17, 12, 7, 2, …? 
Solution. Let an = –150
a + (n – 1)d = –150
⇒ 17 + (n – 1)(–5) = –150 
⇒ (n – 1)(–5) = – 167
⇒ n = 167 + 5/5 = 172/5 = 34 , 2/5
Here, n is not a natural number.
∴ –150 is not a term of the given AP.

Question. The eighth term of an AP is half its second term and the eleventh term exceeds one-third of its fourth term by 1. Find the 15th term. 
Solution. 3

Question. Find the 10^th term from end of the AP: 4, 9, 14, …, 254.
Solution. 209

Question. The angles of a triangle are in AP. The greatest angle is twice the least. Find all the angles of the triangle.
Solution. 40°, 60°, 80°

Question. If 4 times the 4^th term of an AP is equal to 18 times the 18^th term, then find the 22nd term.
Solution. Let a₁, a₂, a₃, … a_n, … be the AP with its first term a and common difference d.
It is given that
4a₄ = 18a18 (1)
⇒ 4(a + 3d) = 18(a + 17d) (1)
⇒ 4a + 12d = 18a + 306d (1)
⇒ 14a + 294d = 0 ⇒ 14(a + 21d) = 0 (1)
⇒ a + 21d = 0 ⇒ a + (22 – 1)d = 0
⇒ a₂₂ = 0
Thus, 22nd term is 0.

Question. Find the number of two-digit numbers which are divisible by 6. 
Solution. Two-digit numbers which are divisible by 6 are 12, 18, 24,
…, 96
∴  Last term,
a_n = 96
⇒ 12 + (n – 1)6 = 96 (1)
⇒ (n – 1)6 = 96 – 12 = 84
⇒ n = 15
∴ There are 15 two-digit numbers divisible by 6.

Question. How many three digit numbers are divisible by 11? 
Solution. Three-digit numbers which are divisible by 11 are 110,
121, 132, …, 990
Let an = 990 (1)
⇒ a + (n – 1)d = 990
⇒ 110 + 11(n – 1) = 990
∴ n = 81
Hence, there are 81 three-digit numbers which are divisible by 11.

Question. If m times the mth term of an Arithmetic Progression is equal to n times its nth term and m ≠ n, show that the (m + n)th term of the AP is zero. 
Solution. We know that an = a + (n – 1)d
From the given conditions,
m[a + (m – 1) d] = n[a + (n – 1)d] 
⇒ m[a + (md – d)] = n[a + nd – d]
⇒ am + m²d – md = an + n²d – nd
⇒ am – an + m²d – n²d – md + nd = 0
⇒ a(m – n) + d(m² – n²) – d(m –n) = 0
⇒ a(m – n) + (m + n) (m – n)d – (m – n)d = 0 
⇒ (m – n) [a + (m + n) d – d] = 0
⇒ a + md + nd – d = 0 (1)
⇒ a + (m + n –1)d = 0
Since, m ≠ n, it is clear that (m + n)th term of the AP is zero.

Question. The 4^th term of an AP is zero. Prove that the 25^th term of the AP is three times its 11th term. 
Solution. a⁴ = a + (4 – 1)d
0 = a + 3d
⇒ a = –3d [∴ Given, a4 = 0]
Now a₂₅ = a + (25 – 1)d = a + 24d
= –3d + 24d = 21d = 3 × 7d
Hence, a₂₅ = 3 × a₁₁
[∴ Since a₁₁ = a + (11 – 1)d = –3d + 10d = 7d] 

Question. For what value of n, the nth term of two APs: 63, 65, 67, … and 3, 10, 17, … are equal. 
Solution. 13

Question. The 8^th term of an AP is 37 and its 12^th term is 57. Find the AP. 
Solution. 2, 7, 12, 17, 22, …

Question. The sum of the 4^th and 8^th terms of an AP is 24 and the sum of the 6th and 10^th terms is 44. Find the first three terms of the AP. 
Solution. –13, –8, –3

Question. Find the number of natural numbers between 102 and 998 which are divisible by 2 and 5 both.
Solution. 110, 120, 130, … , 990
a_n = 990
⇒ 110 + (n − 1) × 10 = 990
∴ n = 89

Question. Which term of the AP: 115, 110, 105, ….. is its first negative term?
Solution. 25^th term

Sum of nature of an Arithmetic Progression

Question. If the mean of the first n natural number is 15, then find n. 
Solution. The natural number are, 1, 2, 3 ….. n
Their, mean = S_n/ n and S_n = n/2 [2a + (n -1) d]
The mean of first n natural numbr is n n (n + 1)/2n
is n + 1/ 2
∴ n + 1/ 2 = 15, (given)
⇒ n = 29

Question. If in an A.P., a = 15, d = – 3 and an = 0, then find the value of n.
Solution. Given, for an A.P., a = 15, d = – 3 and an = 0
Now, a_n = a + (n – 1)d
⇒ 0 = 15 + (n – 1) × (– 3)
⇒ (n – 1) = 5
⇒ n = 6
Hence, the value of n is 6.

Question. Find the number of terms in the A.P. : 18, 15 ,1/ 2, 13, …, – 47.
Solution.

Question. Find the common difference of the Arithmetic Progression (A.P.)
1/a’ 3 – a / 3a , 3 – 2a /3a , … (a ≠ 0 )
Solution. Given: Arithmetic progression (AP) is
1/a’ 3 – a / 3a , 3 – 2a /3a , … (a ≠ 0 )

Question. Write first four terms of each of the following sequence, whose general terms are:
(i) a_n = 3n – 7 (ii) a_n = (– 1)ⁿ⁺¹ × 3ⁿ
Solution. (i) an = 3n – 7
∴ a₁ = 3 × 1 – 7 = 3 – 7 = – 4, a2 = 3 × 2 – 7 = 6 – 7 = – 1,
a₃ = 3 × 3 – 7 = 9 – 7 = 2 and a4 = 3 × 4 – 7 = 12 – 7 = 5
(ii) a_n = (– 1)ⁿ⁺¹ × 3ⁿ
⇒ a₁ = (– 1)¹⁺¹ × 31 = 3,
∴ a₂ = (– 1)²⁺¹ × 3² = (–1)³ × 3² = –9,
a₃ = (– 1)⁴ × 3³ = 27 and a₄ = (– 1)⁵ × 3⁴ = – 81

Question. What is 18^th term of the sequence defined by an = n(n – 3)/n + 4  ?
Solution. We have,

Question. Justify whether it is true to say that –1, – 3 /2 , –2, 5/ 2 , … form an AP as a₂ – a₁ = a₃ – a₂.
Solution. False
Explanation: The given series of numbers is –1, -3 / 2 , –2,5 / 2

⇒ a₂ – a₁ = a₃ – a₂
but a₃ – a₂ ≠ a₄ – a₃
Clearly, the difference of two successive terms is not the same, hence we can say that the given list of numbers does not form an AP.

Question. Two AP’s have the same common difference. The first term of one AP is 2 and that of the other is 7. The difference between their 10^th terms is the same as the difference between their 21^st terms, which is the same as the difference between any two corresponding terms. Why?
Solution. Let d be the common difference of two AP’s First term of first AP is 2.
First AP will be 2, 2 + d, 2 + 2d …
First term of second AP is 7 second AP will be
7, 7 + d, 7 + 2d …
We know that an = a + (n – 1)d
10^th term of first AP = 2 + 9d
10^th term of second AP = 7 + 9d
(i)erence of their 10th term = (7 + 9d) – (2 + 9d)
= 7 + 9d – 2 – 9d
= 5
Again, 21st term of first AP = 2 + 20d
21^st term of second AP = 7 + 20d
(i)erence of their 21st term
= (7 + 20d) – (2 + 20d)
= 7 + 20d – 2 – 20d = 5
Thus, we can say that if an and bn are nth terms of first and second AP respectively, then
b_n – a_n = [7 + (n – 1)d] – [2 + (n – 1)d]
= 7 + (n – 1)d – 2 – (n – 1)d = 5
⇒ b_n – a_n = 5
Hence, the difference between any two corres- ponding terms of such AP’s is the same as the difference between their first terms.

Question. How many 2-digit numbers are divisible by 3? 
Solution. Two digits numbers divisible by 3 are 12, 15, 18 …, 99
Here, first term, a = 12
common difference, d = 15 – 12 = 18 – 15 = 3
last term, an = 99
Now, nth term, an = a + (n – 1)d,
where, ‘n’ is the number of the terms
⇒ 99 = 12 + (n – 1) 3
⇒ 99 = 12 + 3n – 3
⇒ 3n = 90
⇒ n = 30
Hence, the number of terms are 30.

Question. In an AP, if the common difference (d) = – 4, and the seventh term (a7) is 4, then find the first term. 
Solution. Given: common difference (d) of an A.P. = – 4
Seventh term (a7) of A.P. = 4
Let, ‘a’ be the first term of the A.P.
Then, a7 = a + (n – 1)d
⇒ 4 = a + (7 – 1) (– 4)
⇒ 4 = a – 24
⇒ a = 28
Hence, the first term of the A.P, is 28.

Question. If the nth term of the A.P. –1, 4, 9, 14, …. is 129, find the value of n. 
Solution. Given, A.P. is –1, 4, 9, 14, ……
nth term, an = 129
Here, first term, a = –1
Common difference, d = 4 – (–1) = 5
∴ a + (n – 1)d = 129
⇒ – 1 + (n – 1)5 = 129
⇒ – 1 + 5n – 5 = 129
⇒ 5n – 6 = 129
⇒ 5n = 135
⇒ n = 27
Hence, the value of n is 27.

Question. Find the 9th term from the end (towards the first term) of the A.P. 5, 9, 13, …., 185.
Solution. Given A.P. is 5, 9, 13, …., 185, Since we have to find the 9^th term from the end,
We should reverse the A.P. Then, it will become easier to find the 9^th term from the starting:
185, 181, ……, 13, 9, 5
Now, first term, a = 185
Common difference,
d = 181 – 185 = – 4
Then, 9th term of A.P.,
a9 = a + (9 – 1) × d
[∵ an = a + (n – 1)d]
= 185 + 8 × (– 4)
= 185 – 32 = 153
Hence, the 9^th term from the end is 153.

Question. For the AP: -3, -7, -11, …, can we directly find a30 – a20 without actually finding a30 and a20? Give reasons for your answer.
Solution. Yes, we can find.
The given list of numbers of an AP –3, –7, –11 …
We know that an = a + (n – 1)d
⇒ a30 = a + (30 – 1)d = a + 29d
⇒ a₂₀ = a + (20 – 1)d = a + 19d
Now, a₃0 – a₂0 = (a + 29d) – (a + 19d)
= a + 29d – a – 19d = 10d …(i)
For the given series, common difference, d = –7 – (–3) = –7 + 3 = –4
Hence, a30 – a20 = 10d = 10(–4) = –40
[Using eqn. (i)]
a₃0 – a₂0 = –40

Question. If the first three terms of an A.P. are b, c and 2b, then find the ratio of b and c.
Solution. b, c and 2b are in A.P
⇒ c = 2b /3
∴ b : c = 2 : 3

Question. Find the sum of the first 100 natural numbers. 
Solution. The list of first 100 natural numbers. 1, 2, 3, ……, 100, which forms an AP with a = 1, d = 1 So,
S₁₀₀ = 100 /2 [2×1+ (100−1)(1)]
= 50 [101]
= 5050

Question. What is the common difference of an A.P. in which a₂₁ –a₇ = 84?
Solution.

Question. Find the 16th term of the AP: 2, 7, 12, 17, …..…….
Solution. Here, first term, a = 2 and common difference, d = 5.
Using formula, nth term, an = a + (n – 1).d
So, a16 = a + 15 d
= 2 + 15 × 5
= 2 + 75 = 77

Question. Find the mean of first eleven natural numbers.
Solution. Mean = 1 + 2 + 3 + _ + 11 / 11 = 11 ( 11 + 1) / 2 x 11 = 6 
[∴ Sum of first n numbers n(n + )/2]

Question. Show that (a – b)², (a² + b²) and (a + b)² are in AP.
Solution. (a – b)², (a² + b²) and (a + b)2 will be in AP, if 2(a² + b²) = (a – b)² + (a + b)²
L..H.S. = (a² – b²) + (a² + b²)
= a² + b² – 2ab + a² + b² + 2ab
= 2(a² + b²) = R.H.S.
Hence, (a – b)², (a² + b²) let (a + b)² are in A.P.

Question. For what value of k will k + 9, 2k – 1 and 2k + 7 are the consecutive terms of an A.P.?
Solution.

Question. If the 17^th term of an A.P. exceeds its 10^th term by 7, find the common difference.
Solution. Given : a17 = a10 + 7 …(i)
Let ‘a’ be the first term of A.P. and ‘d’ be its
common difference.
Then a₁₀ = a + (10 – 1)d = a + 9d
and a₁₇ = a + (17 – 1)d = a + 16d
put the values in (i), we get:
a + 16d = a + 9d + 7
⇒ 7d = 7
⇒ d = 1
Hence, the common difference of given A.P. is 1.

Question. Write the n^th term of the A.P.
1/m , 1+ m /m , 1 + 2m + m / m ,…….. 
Solution. Given, A.P. is 1/m , 1+ m /m , 1 + 2m + m / m ,……..

Question. How many multiples of 4 lie between 10 and 205 ?
Solution. Multiples of 4 between 10 and 205 is 12, 16, 20, 24, 28, ……, 204.
Let, the number of multiples be ‘n’.
Here, first term, a = 10
common difference, d = 4
last term, an = 204
Since, nth therm of an A.P. is an = a + (n – 1)d
⇒ 204 = 12 + (n – 1) × 4
⇒ 204 = 12 + 4n – 4
⇒ 4n = 204 – 8
⇒ n = 196 /4 = 49
Hence, the number of multiples of 4 are 49.

Question. Determine the A.P. whose third term is 16 and 7th term exceeds the 5th term by 12.
Solution. Let, the first term of an A.P. be “a’ and common difference be ‘d’.
Given, a₃ = 16
i.e., a + (3 – 1)d = 16
⇒ a + 2d = 16 …(i)
and a7 = a5 + 12 (given)
a + (7 – 1)d = a + (5 – 1)d + 12
⇒ a + 6d = a + 4d + 12
⇒ 2d = 12
⇒ d = 6
If we put the value of d in equation (i), we get
a + 2 × 6 = 16
⇒ a = 4
∴ The first term of the A.P is 4 and its common
difference is 6.
Hence, the required A.P. is 4, 10, 16, 20……..

Question. Which term of the AP 3, 15, 27, 39, …. will be 120 more than its 21st term ? 
Solution. Given: A.P. is 3, 15, 27, 39, …….
Here, the first term, a = 3
Common difference, d = 15 – 3 = 27 – 15 = 12.
Now, 21st term:
a21 = 3 + (21 – 1) × 12
= 3 + 20 × 12
= 3 + 240 = 243
According to the given condition :
an = a₂₁ + 120
where, an is the nth term
an = 243 + 120
⇒ a + (n – 1)d = 363
⇒ 3 + (n – 1) × 12 = 363
⇒ (n – 1) = 360 /12
⇒ n = 31
Hence, the 31st term is 120 more than the 21^st term.

Question. If seven times the 7^th term of an A.P. is equal to eleven times the 11^th term, then what will be its 18^th term ?
Solution. Let the first term of the A.P. be ‘a’ and its common difference be ‘d’.
Given, 7a₇ = 11a₁₁
Then, 7(a + 6d) = 11(a + 10d)
[Q an + a + (n – 1)d]
⇒ 7a + 42d = 11a + 110d
⇒ 7a – 11a = 110d – 42d
⇒ – 4a = 68d
⇒ a = – 17d
Now, 18^th term of A.P.
a₁₈ = a + (18 – 1)d
= a + 17d
putting a = – 17d
= –17d + 17d
a₁₈ = 0
Hence, the 18^th term of A.P. is 0.

Question. The 10^th term of an A.P. is –4 and its 22nd term is (– 16). Find its 38^th term.
Solution. Let, the first term of A.P. be ‘a’ and its common
difference be d’.
a10 = – 4 (given)
i.e. a + 9d = – 4 …(i)
a₂₂ = – 16 (given)
a + 21d = – 16 …(ii)
On solving (i) and (ii), we get   

If we put the value of d = – 1 in equation (i), we get
a = – 4 + 9 = 5
∴ first term, a = 5
and common difference, d = – 1
38^th term, a38 = a + (38 – 1)d
= 5 + 37(– 1)
= – 32
Hence, the 38th term of the A.P. is – 32.

Question. Find how many integers between 200 and 500 are divisible by 8. 
Solution. Integers between 200 and 500 divisible by 8
are 208, 216, 224 ,…, 496.
This series foums an A.P., where first term, a = 8
common difference, d = 8
and last term, l = 496
Let, the number of integers be ‘n’
Then, nth term = an (last term l) = a + (n – 1)d
496 = 208 + (n – 1) × 8
⇒ (n – 1) × 8 = 496 – 208
⇒ (n – 1) = 288 /8
⇒ n = 37
Hence, the number of terms are 37.

Question. Determine the AP whose third term is 5 and the seventh term is 9. 
Solution. Given, third term of A.P., a₃ = 5
Seventh term of A.P., a7 = 9
Let the first term of A.P. be ‘a’ and its common
difference be ‘d’.
Now, a3 = a + (3 – 1)d
or 5 = a + 2d …(i)
and a7 = a + (7 – 1)d
or 9 = a + 6d …(ii)
On solving (i) and (ii), we get 4d = 4
⇒ d = 1
If we put the value of ‘d’ in equation (i), we get:
5 = a + 2 × 1
⇒ a = 3
Hence, the A.P. is 3, 4, 5, 6.

Question. If the sum of the first 9 terms of an AP is equal to the sum of its first 11 terms, then find the sum of its first 20 terms. 
Solution. Let, the first term of an A.P. be ‘a’ and its common difference be ‘d’.
Given, S₉ = S₁₁
⇒ 9 / 2
[2a + (9 – 1)d] = 11/ 2 [2a + (11 – 1)d]
∵ S n = n/2[2a + (n −1) d ]
⇒ 9[2a + 8d] = 11[2a + 10d]
⇒ 18a + 72d = 22a + 110d
⇒ 4a = – 38d
⇒ 2a = – 19d …(i)
Now, sum of first 20 terms:
S₂₀ = n /2 [2a + (n – 1)d]
= 20/ 2 [2a + (20 – 1)d]
= 10[– 19d + 19d]
[from (i)]
= 10 × 0 = 0
Hence, the sum of first 20 terms is 0.

Question. The first term of an AP is -5 and the last term is 45. If the sum of the terms of the AP is 120, then find the number of terms and the common difference. 
Solution. Let a be the first term, d be the common difference and n be the number of terms.
It is given that:
first term, a = –5
Last term, L = 45
We know that, if the last term of an AP is
known, then the sum of n terms of an AP is
S_n = n /2 ( a+l )
120 = n /2 (−5+45)
120 × 2 = 40 × n
⇒ n = 6
L = a + (n – 1)d
⇒ 45 = –5 + (6 – 1)d
⇒ 50 = 5d ⇒ d = 10
Hence, number of terms = 6
and common difference = 10

Question. Find the number of natural numbers between 102 and 998 which are divisible by 2 and 5 both.
Solution. 110, 120, 130, … , 990
a_n = 990
⇒ 110 + (n − 1) × 10 = 990
∴ n = 89

Question. For what value of n, are the nth terms of two A.Ps 63, 65, 67,… and 3, 10, 17,… equal? 

Question. The common difference between the terms of two AP’s is same. If the difference between their 50th terms is 100, what is the difference between their 100th terms? 
Solution. Let a₁ and a₂ be the first terms of two AP’s
and d be their common difference.
(a1 + 49d) – (a₂ + 49d) = 100
a₁ – a₂ = 100 …(i)
Then, difference between their 100th terms is
(a1 + 99d) – (a₂ + 99d) = a1 – a2 [Using (i)]
= 100
The difference between their 100th terms is
100 i.e., same as difference in 50th terms.

Question. In an AP, if S₅ + S₇ = 167 and S₁₀ = 235, then find the AP, where S_n denotes the sum of its first n terms.
Solution. S₅+ S7 = 167
⇒  5/2 [2a + 4d]+ 7/2 [2a + 6d] = 167
24a + 62d = 334
or 12a + 31d = 167 …(i)
S₁₀ = 235
⇒ 5[2a + 9d = 235 or 2a + 9d = 47 …(ii)
Solving (i) and (ii) to get a = 1, d = 5.
Hence AP is 1, 6, 11, …..

Question. The 4^th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11^th term.   

Question. If S_n, the sum of first n terms of an AP is given by Sn = 3_n² – 4_n, find the nth term.
Ans. Here, the nth term Sn = 3_n² – 4_n
∴ S_n – 1 = 3 (n – 1)2 – 4(n – 1)
= 3n² – 10n + 7
Hence, the nth term,
an = Sn – Sn – 1
= (3n² – 4n) – (3n² – 10n + 7)
= 3n² – 4n – 3n² + 10n – 7
an = 6n – 7
Hence, the nth term is 6n – 7.

Question. Find the sum of first 8 multiples of 3. 
Solution. First 8 multiple of 3 are:
3, 6, 9, 12, 15, 18, 21, 24, which forms an A.P.
S_n = 3 + 6 + 9 + 12 + …… + 24
Here, first term, a = 3
common difference, d = 3
number of terms, n = 8
S_n = n /2
[2a + (n – 1)d] = 8/ 2
[2 × 3 + (8 – 1)3]
= 4[6 + 21] = 4 × 27 = 108
Thus, the sum of the first 8 multiples is 108.

Question. For an A.P., it is given that the first term (a) = 5, common difference (d) = 3, and the n^th term (a_n) = 50. Find n and the sum of first n terms (S_n) of the A.P. 
Solution. Here, a = 5, d = 3 and an = a + (n – 1) d = 50
⇒ 5 + 3 (n – 1) = 50
⇒ 3(n – 1) = 45
⇒ n – 1 = 15
or n = 16
∴ Number of terms, n = 16
Now. = S16 = 16 / 2 [2 x 5 + (16 -1) (3 )]
[∴ S_n = n/ z (2a + (n – 1)d)]
= 8[10 + 45]
= 440.

Question. If 6 times the 6^th term of an A.P. is equal to 9 times the 9^th term, show that its 15^th term is zero.
Solution. Let a be the first term and d be the common difference of the AP.
Given, a₆ = 9 × a9
Thus, 6(a + 5d) = 9(a + 8d)
⇒ 3a = – 42d
or a + 14d = 0 …(i)
Thus, a₁₅ = a + 14d = 0 (by (i))
Hence, 15^th term of the AP is zero.

Question. Find the sum of all 11 terms of an A.P., whose middle term is 30.
Solution. Let ‘a’ be the first term and d, the common difference of the given A.P.
Then, the middle term = a6 = a + 5d = 30.
Now, S₁₁ = 11/ 2 [2a + 10 d]
= 11/ 2 × 60
   [∵ a + 5d = 30]
= 330

Question. Two AP’s have the same common difference. The difference their between their 100^th terms is 100, what is the difference between 1000^th terms. 
Solution. Let a₁ and a₂ are two AP’s and their common difference be d.
According to question,
[a₁ + (100 – 1)d] – [a₂ + (100 – 1)d] = 100
[∵an = a + (n – 1)d]
⇒ [a1 + 99d] – [a₂ + 99d] = 100
⇒ a₁ – a₂ =100 …(i)
Now, to find the difference between their 1000^th terms
[a₁ + (1000 – 1)d] – [a2 + (1000 – 1)d]
= a₁ + 999d – a₂ – 999d
= a₁ – a₂ By equation (i), we get
[a1 + (1000 – 1)d] – [a₂ + (1000 – 1)d]
= a₁ – a₂ = 100
Therefore, difference between their 1000^th terms would be equal to 100.

Question. Justify whether it is true to say that the following are the nth terms of an AP:
(i) 2n – 3 (ii) 3n² + 5
(iii) 1 + n + n²
Solution. (i) Yes, (2n – 3) is the nth term of an A.P. It is given that
an = 2n – 3
Put n = 1, a₁ = 2(1) – 3 = 2 – 3 = –1
n = 2, a₂ = 2(2) – 3 = 4 – 3 = 1
n = 3, a₃ = 2(3) – 3 = 6 – 3 = 3
n = 4, a₄ = 2(4) – 3 = 8 – 3 = 5
List of numbers becomes –1, 1, 3, 5…
Here, a₂ – a1 = 1 – (–1) = 2
a₃ – a₂ = 3 – 1 = 2
a₄ – a₃ = 5 – 3 = 2
Clearly, a₂ – a₁ ≠ a₃ – a₂ = a₄ – a₃
Hence, 2n – 3 is the nth term of an AP.
(ii) No, (3n² + 5) is not the nth term of an AP.
It is given that an = 3n² + 5
Put n = 1, a₁ = 3(1)² + 5 = 3 + 5 = 8
n = 2, a₂ = 3(2)² + 5 = 12 + 5 = 17
n = 3, a₃ = 3(3)² + 5 = 27 + 5 = 32
List of number becomes 8, 17, 32 …
Here, a₂ – a₁ = 17 – 8 = 9,
a₃ – a₂ = 32 – 17 = 15
Clearly, a₂ – a₁ = a₃ – a₂
Hence, (3n² + 5) is not the nth term of an AP.
(iii) No, (1 + n + n²) is not the nth term of an AP.
It is given that an = 1 + n + n²
Put n = 1, a₁ = 1 + (1) + (1)²
= 1 + 1 + 1 = 3
n = 2, a₂ = 1 + (2) + (2)²
= 1 + 2 + 4 = 7
n = 3, a₃ = 1 + (3) + (3)²
= 1 + 3 + 9 = 13
List of number becomes 3, 7, 13 …
Here, a₂ – a₁ = 7 – 3 = 4
a₃ – a₂ = 13 – 7 = 6
Clearly, a₂ – a₁ ≠ a₃ – a₂
Hence, (1 + n + n²) is not the nth term of an AP.

Question. Find the sum of first 15 multiples of 8. 
Solution. Multiples of 8 are : 8, 16, 24 …,
Since, the difference between the numbers is constant, so it forms an A.P.We need to find the sum of first 15 multiples.
Sn = n/ 2 (2a + (n – 1)d)
Here, n = 15, a = 8 and d = 8
∴  S₁₅ = 15/ 2 [2 × 8 + (15 – 1) × 8]
= 15/ 2 (16 + 14 × 8)
= 15/ 2 [16 + 112]
= 15 /2 × 128 = 960
Hence, the sum of first 15 multiples of 8 is 960.

Question. Find a, b and c such that the following numbers in AP: a, 7, b, 23, c. 
Solution. It is given that a, 7, b, 23, c are in AP
they have a common difference
i.e., 7 – a = b – 7 = 23 – b = c – 23
Taking second and third terms, we get
b – 7 = 23 – b ⇒ 2b = 30 ⇒ b = 15
Taking first and second terms, we get
7 – a = b – 7
⇒ 7 – a = 15 – 7 [As b = 15]
⇒ 7 – a = 8 ⇒ a = –1
Taking third and fourth terms, we get
23 – b = c – 23
⇒ 23 – 15 = c – 23 [As b = 15]
⇒ 8 = c – 23 ⇒ c = 31
Hence, a = –1, b = 15 and c = 31.

Question. Determine the AP whose 5th term is 19 and the difference of the 5^th term from the 13^th term is 20. 
Solution. Let the first term of an AP be a and commom difference be d.
It is given that a5 = 19
and a₁₃ – a₈ = 20
We know that an = a + (n – 1) d
a₅ = a + (5 – 1) d = a + 4d = 19 …(i)
Also, a₁₃ – a₈ = 20
⇒ (a + 12d) – (a + 7d) = 20
⇒ a + 12d – a – 7d = 20
⇒ 5d = 20 ⇒ d = 4
Putting the value of d = 4 in equation (i), we get
a + 4d = 19
⇒ a + 4(4) = 19
⇒ a + 16 = 19
⇒ a = 3
So, the required AP will be
a, a + d, a + 2d, a + 3d …
i.e. , 3, 3 + 4, 3 + 2(4), 3 + 3(4) …
i.e., 3, 7, 11, 15 …

Question. Which term of the A.P. 20, 19 ,1/4 , 18 ,1/4 , 17 ,3/ 4 , …. is the first negative term.
Solution. Here, first term a = 20 and common difference
d =  3 / 4
Let an be the first negative term, i.e.,
a + (n – 1)d < 0
⇒ 20 – 3/ 4 (n−1) < 0
or 20 – 3/4 n + 3/4 < 0
or 3/4 n < 83/4
or n > 83/ 3
So, the nth term is 28.

Question. Find the middle term of the A.P. 7, 13, 19, …., 247.
Solution. Here, first term, a = 7, common difference d = 6
Let AP contains ‘n’ terms. Then, an = 247
⇒ a + (n – 1) d = 247
⇒ 7 + 6(n – 1) = 247
⇒ n – 1 = 40
or n = 41
So, the middle term is 21^st term
a₂₁ = a + (n – 1)d
= 7 + 20 × 6
= 7 + 120, i.e., 127

Question. Split 207 into three parts such that these are in AP and the product of the two smaller parts is 4623.
Solution. Let (a – d), a and (a + d) be three parts of 207 such that these are in AP.
It is given that sum of these numbers = 207
⇒ (a – d) + a + (a + d) = 207
⇒ 3a = 207 ⇒ a = 69
It is also given that product of two smaller parts = 4623
⇒ a(a – d) = 4623
⇒ 69(69 – d) = 4623
⇒ 69 – d = 4623/ 69
⇒ 69 – d = 67
⇒ d = 69 – 67 = 2
So, first part = a – d = 69 – 2 = 67,
second part = a = 69
and third part = a + d = 69 + 2 = 71
Hence, the three parts are 67, 69 and 71.

Question. The sum of the first 30 terms of an A.P. is 1920. If the fourth term is 18, find its 11^th term. 
Solution. Let a be the first term and d, the common difference of the AP
Here, number of terms, n = 30
Then, S₃₀ = 30/ 2 [2a + 29d] = 1920
or 2a + 29d = 128 …(i)
Also, a₄ = a + 3d = 18 …(ii)
On solving equations (i) and (ii), we get
d = 4 and a = 6
Thus, a₁₁ = a + 10d = 6 + 40 = 46.
Hence, 11^th term of the AP is 46

Question. How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3? 
Solution. Numbers that lie between 10 and 300 are 11, 12, … 299. Numbers between 10 and 300 which when divided by 4 leave a remainder 3 and are 11, 15, 19, …299
Here, first number, a = 11
and common difference, d = 4
number of terms, n = ?
We know that an = a + (n – 1)d
a + (n – 1)d = 299
⇒ 11 + (n – 1)(4) = 299
⇒ 11 + 4_n – 4 = 299
⇒ 4_n = 292 ⇒ n = 73

Question. Find the sum of the two middle most terms of the AP:
 4 / 3 , – 1 , – 2/3 ,……. 4 ,1/ 3
Solution.

Question. Show that the sum of all terms of an A.P. whose first term is a, the second term is b and the last term is c is equal to
(a + c) (b + c – 2a)/2(b – a)
Solution. Here, first term is a, and, common difference = b – a = d and last term is c.   

Question. Which term of the A.P. 19, 18,1/5 , 17 , 2/5 .. ……is the first negative term?   
Solution.

Question. How many numbers of two digits are exactly divisible by 8?
Solution. We observe that 16 is the first two digit number divisible by 8 and 96 is the last two digit number divisible by 8. Thus, we have to determine the number of terms in the sequence 16, 24, 32, …., 96.
Clearly, it is an A.P. with first term = 16 and common difference = 8, i.e. a = 16, d = 8.
Let there be n terms in this A.P. Then, an = 96
⇒ a + (n – 1) d = 96
⇒ 16 + (n – 1) (8) = 96
⇒ 8 (n – 1) = 80 ⇒ n – 1 = 10 ⇒ n = 11
Hence, there are 11 numbers of two digits which are divisible by 8.

Question. A ladder has rungs 25 cm apart (see figure). The rungs decrease uniformly in length from 45 cm at the bottom and 25 cm at the top. If the top and the bottom rungs are 2,1/2 m apart, what is the length of the wood required for the rungs?
Solution. Distance between rung at the top and the bottom = 2,1/2 m = 250m   

Distance between two consecutive rungs = 25 cm.

Question. The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house number x is equal to the sum of the numbers of the houses following it. Find this value of x.
Solution. Let the number of houses before house no. x = x – 1.

Since, house numbers are consecutive, so sum of house numbers preceding house x

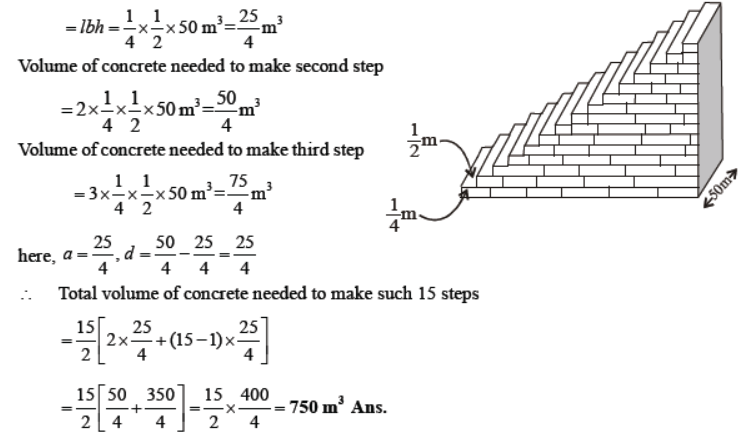
Question. A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of 1/4 m and a tread of 1/2 m (see figure). Calculate the total volume of concrete required to build the terrace. 
Solution. Volume of concrete needed to make first step

Question. Find the sum of the first 25 terms of an A.P. whose nth term is given by an = 7 – 3n.     
Solution. We have, a_n = 7-3_n
Putting n = 1, we get a₁ = 7 – 3(1) = 4
Putting n = 25, we get a ₂₅ = 7 – 3(25) = -68
so, for the given A.P., we have, first then = a = 4 and 25th term = – 68.

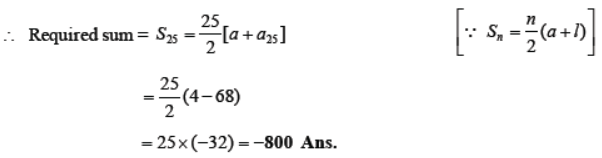
Question. How many terms of the series 54, 51, 48, ….. be taken so that their sum is 513?   
Solution. Clearly, the given sequence is an A.P. with first term a ( = 54) and common difference d (= – 3). Let the sum of n terms be 513. Then,

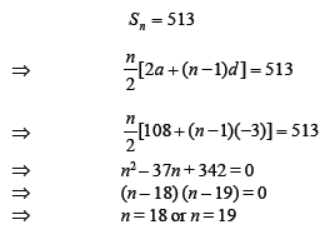
Here, the common difference is negative. So, 19th term is given by 19 a10 = 54 + (19 -1)x (-3) = 0.
Thus, the sum of 18 terms as well as that of 19 terms is 513.

Question. In an A.P., the sum of first n terms is 3n2/2 + 5n/2 . Find its 25^th term.     
Solution. Let s_n denote the sum of n terms of an A.P. whose nth term is a_n

Question. If the sum of the first 10 terms of an A.P. is 110 and the sum of first 20 terms is 420, find the sum of first 30 terms of this A.P.   
Solution. Let the first term be a and the common difference be d. Now,
Given s₁₀ = 110

Question. A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows : Rs. 200 for the first day, Rs. 250 for the second day, Rs. 300 for the third day, etc. the penalty for each succeeding day being Rs. 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days? 
Solution. Clearly, the amount of penalty for different days forms an A.P. with first term a (= 200) and common difference d (=50). According to question, we have to find the sum of 30 terms of this A.P. 

Question. A spiral is made up of successive semicircles, with centres alternatively at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 2.0 cm, as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? [ Take π = 22/7]   

Solution.

Question. 200 logs are stacked in the following manner : 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on (see diagram). In how many rows the 200 logs are placed and how many logs are in the top row? 

Solution. Here, a_n = 20, d = 1, Sn = 200
Now, a_n = 20
⇒ a + (n – 1) d = 20
⇒ a + (n – 1) (1) = 20
⇒ a + n = 21

Question. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see diagram). Find the total distance travelled for placing the ten potatoes from a line into the bucket. 

Solution. Clearly, the competitor is to cover double distance in order to get the potato from the place and to be placed in the bucket.
Distance between bucket and Ist potato = 5 m
Distance between bucket and 2nd potato = (5 + 3) m = 8 m
Distance between bucket and 3rd potato = (8 + 3) m = 11 m
here, a = 5, d = 8 – 5 = 3
∴ Total distance travelled for placing 10 potatoes in the bucket
= 2(5 + 8 + 11 + …….. upto 10 terms)

Question. A sequence an is defined by an = 5 – 2n. Prove that it is an AP.   
Solution. 

Question. Which term of the A.P. 5, 15, 25, …. will be 130 more than its 31st term?   
Solution. We have, a = 5, d = 10
⇒ a₃₁ = a + (31-1)d = a + 30d = 5 + 30×10 = 305.
Let nth term of the given A.P. be 130 more than its 31^st term.
Then, a_n = 130 + a₃₁
⇒ a + (n – 1) d = 130 + 305
⇒ 5 + 10 (n – 1) = 435 ⇒ 10 (n – 1) = 430 ⇒ n – 1 = 43 ⇒ n = 44.
Hence, 44^th term of the given A.P. is 130 more than its 31st term.

Question. Write down the first six terms of each of the following sequences, whose general terms are:
(a) a_n = 5n – 3 (b) a_n = (– 1)n ⋅ 2²ⁿ (c) a_n = 2n + 1/n + 2 (d) a_n = (–1)^{n – 1} ⋅ n²
Solution. (a) 2, 7, 12, 17, 22, 27
(b) –4, 16, –64, 256, –1024, 4096
(c) 1,5/4 , 7/5 , 3/2 , 11/7, 13/8
(d) 1, –4, 9, –16, 25, –36

Question. Find the 10th term of the sequence defined by an = (–1)2n – 1 ⋅ 5n.
Solution. –9765625

Question. Find the difference between the 12th term and 10^th term of the sequence whose general term is given by an = 5n – 1. 
Solution. 10

Question. For what value of x: 2x, x + 10 and 3x + 2 are in AP?
Solution. Since, given numbers are in AP.
So, (x + 10) – 2x = (3x + 2) – (x + 10)
⇒ –x + 10 = 2x – 8 or 3x = 18 or x = 6

Question. Find the 12^th term from the end of the AP: –2, – 4, – 6, …, – 100. 
Solution. Let a be the first term, d the common difference and l the last term of AP.
Here, a = –2, d = (–4 + 2) = –2, l = –100 and n = 12
∴ n^th term from end = l – (n – 1) d
⇒ 12^th term from end = –100 – (12 – 1) (–2) = –100 + 24 – 2 = –78

Question. The sum of the 5th and 7th terms of an AP is 52 and the 10th term is 46. Find the AP.
Solution. Let the first term and the common difference of an AP be ‘a’ and ‘d’.
∴ a₅ = a + 4d and a₇ = a + 6d
So, a₅ + a₇ = 2a + 10d = 52 ⇒ 2a + 10d = 52 …(i)
Also, a10 = a + 9d = 46 ⇒ a + 9d = 46 …(ii)
From (i) and (ii), d = 5 and a = 1
So, the AP is as follows 1, 6, 11, 16, 21, …

Question. Find the 25^th term of the AP: – 5 , -5/2 ,0 , 5/2 , …..
Solution. We have, a = –5, d = -5/2 – (-5) = 5/2
∴ an = a + (n – 1) d
∴ a₂₅ = (– 5) + (25 – 1) 5/2 = (− 5) + 24 (5/2) = -5 + 60 = 55

Question. Find the 31^st term of an AP whose 11^th term is 38 and the 16th term is 73.       
Solution. Let the first term be a and common difference be d.
Now, given a₁₁ = 38 ⇒ a + (11 – 1)d = 38
⇒ a + 10 d = 38 …(i)
Also, a₁₆ = 73 fi a + (16 – 1) d = 73
⇒ a + 15d = 73 …(ii)
Now, subtracting (ii) from (i), we get

Putting the value of d in equation (i), we get
a + 10 × 7 = 38 ⇒ a + 70 = 38
⇒ a = 38 – 70 ⇒ a = –32
We have a = –32 and d = 7
Therefore, a₃₁ = a + (31 – 1)d = a + 30 d
⇒ a₃₁ = (–32) + 30 × 7 = –32 + 210 ⇒ a31 = 178

Question. The first term of an AP is x and its common difference is y. Find its 12^th term.
Solution. a₁₂ = a + 11d = x + 11y.

Question. Which term of the AP: 3, 8, 13, 18, …, is 78? 
Solution. Let an be the required term of the AP: 3, 8, 13, 18,…
Here, a = 3, d = 8 – 3 = 5 and an = 78
Now, an = a + (n – 1)d
⇒ 78 = 3 + (n – 1) × 5 ⇒ 78 – 3 = (n – 1) × 5
⇒ 75 = (n – 1) × 5 ⇒ 75/5 = n – 1
⇒ 15 = n – 1 ⇒ n = 15 + 1 = 16
Hence, 16^th term of given AP is 78.

Question. An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
Solution. Let a be the first term and d be the common difference.
Since, given AP has 50 terms, so n = 50
∴ a₃ = 12 ⇒ a + (3 – 1) d = 12
⇒ a + 2d = 12 …(i)
Also, a₅₀ = 106 ⇒ a + (50 – 1) d = 106
⇒ a + 49d = 106 …(ii)
Subtracting (i) from (ii), we get
47d = 94 ⇒ d = 94/47 = 2
Putting the value of d in equation (i), we get
a + 2 × 2 = 12 ⇒ a = 12 – 4 = 8
Here, a = 8, d = 2
So, 29^th term of the AP is given by
a₂₉ = a + (29 – 1)d = 8 + 28 × 2 ⇒ a₂₉ = 8 + 56 ⇒ a29 = 64

Question. In an AP, if d = – 4, n = 7, an = 4, then find the value of a. 
Solution. We have an = 4 for n = 7
∴ an = a + (n – 1) d ⇒ 4 = a + 6(– 4) ⇒ a = 28

Question. Find the 20^th term from the last term of the AP: 3, 8, 13,…, 253. 
Solution. Given, last term = l = 253
And, common difference = d = 8 – 3 = 5 = 13 – 8
∴ 20^th term from end = l – (n – 1) × d = 253 – 19 × 5 = 253 – 95 = 158

Question. Is 0 a term of the AP: 31, 28, 25, …? Justify your answer. 
Solution. Given AP is 31, 28, 25, …
Here, a = 31, d = 28 – 31 = – 3 = 25 – 28
For 0 be a term of this AP, 0 = an for some ‘n’ ⇒ 0 = a + (n – 1)d
⇒ 0 = 31 + (n – 1) (– 3) ⇒ 31 – 3n + 3 = 0
⇒ – 3_n = – 34 ⇒ n = 34/3 = 11,1/3
which is not possible as n cannot be a fraction.
Therefore, 0 cannot be a term of this AP.

Question. How many terms of the AP: 9, 17, 25, … must be taken to give a sum of 636?       
Solution. Let sum of n terms be 636.
Then, Sn = 636, a = 9, d = 17 – 9 = 8

Question. The sum of the first n terms of an AP is 3n² + 6n. Find the nth term of this AP. 
Solution. We have, Sn = 3n² + 6n
S_n–1 = 3(n – 1)2 + 6(n – 1)
= 3(n² + 1 – 2n) + 6n – 6
= 3n² + 3 – 6n + 6n – 6 = 3n²– 3
The nth term will be an
S_n = S_n–1 + an
⇒ a_n = S_n – S_n – 1
= 3n² + 6n – 3n² + 3 = 6n + 3

Question. If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.     
Solution. We have, S₇ = 49

Question. If Sn denotes the sum of the first n terms of an AP, prove that S₃₀ = 3 (S₂₀ – S₁₀).
Solution. We have, Sn = n/2 [2a + (n – 1) d] 

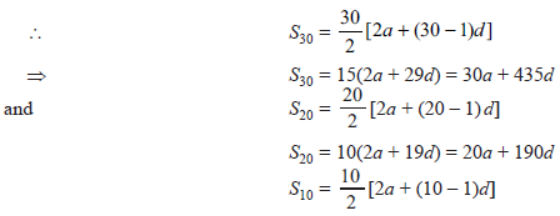
Question. The sum of the first 7 terms of an AP is 63 and the sum of its next 7 terms is 161. Find the 28^th term of this AP. 
Solution. We have, S_n = n/2 [2a + (n – 1)d]  

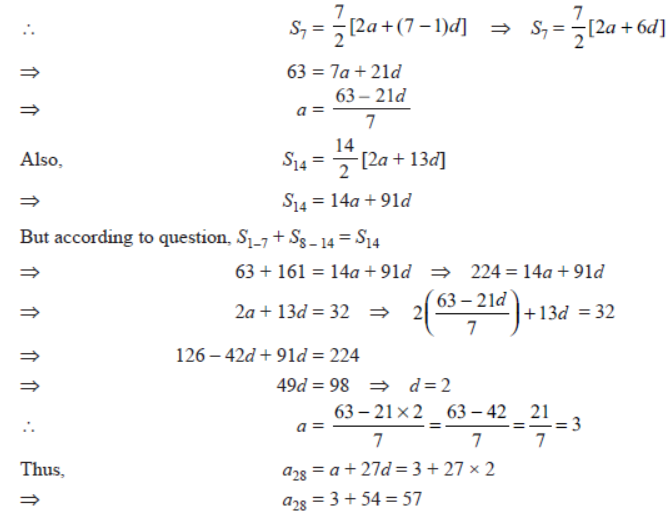
Question. Find the sum:   

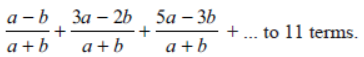
Solution. The first term,

Question In an AP, the sum of first ten terms is – 150 and the sum of next ten terms is – 550. Find the AP.         
Solution. Let a be the first term and d the common difference of the AP.
We have, S₁₀ = – 150

Question. Find the common difference of an AP whose first term is 5 and the sum of its first four terms is half the sum of the next four terms. 
Solution. Given the first term of the AP, a = 5. Let d be the common difference. 
Then, as per the question     

Question. Find the sum of the integers between 100 and 200 that are:       
(i) divisible by 9 (ii) not divisible by 9 
Solution. (i) Numbers divisible by 9 between 100 and 200 are 108, 117, 126, …, 198.
Here, a = 108, d = 9, an = 198
∴ an = a + (n – 1) d ⇒ 198 = 108 + (n – 1) 9

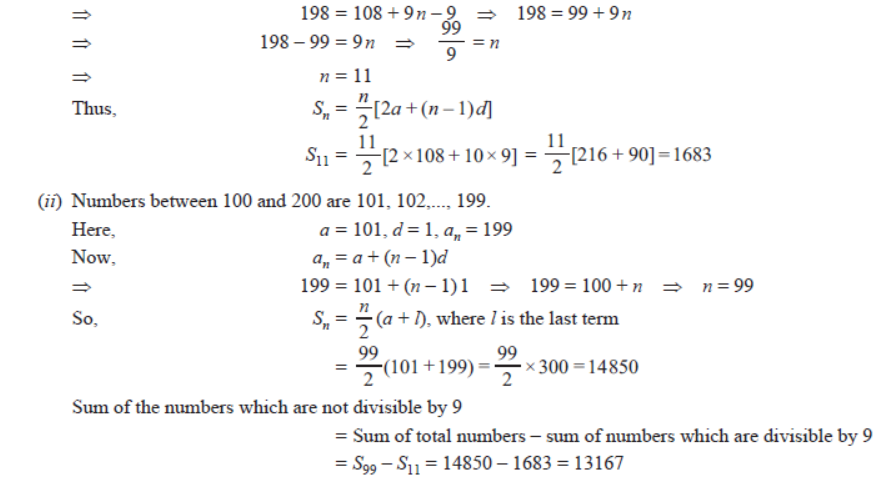
Question. If a_n = 3 – 4_n, show that a1, a², a³, … form an AP. Also find S₂₀. 
Solution. We have, an = 3 – 4n
∴ a₁ = – 1, a₂ = – 5, a₃ = – 9, …
Since a₂ – a₁ = – 4 = a₃ – a₂
So, –1, –5, –9, … form an AP.
S₂₀ = 20/2 [–2 + 19 × (–4)] = 10 [– 2 – 76] = 10 × (–78) = –780

Question. Find the sum of the given AP: – 5 + (– 8) + (– 11) + … + (– 230). 
Solution. We have, a = – 5 and d = –8 + 5 = – 3
So, an = a + (n – 1)d
⇒ – 230 = – 5 + (n – 1) (– 3) ⇒ – 230 = – 5 – 3n + 3
⇒ – 230 + 2 = – 3n ⇒ – 228 = – 3n ⇒ n = 228/3 = 76
∴ S_n = n/2 (a + an) ⇒ S76 = 76/2 [– 5 – 230]
= 38 [– 235] = – 8930

Question. The sum of n, 2n, 3n terms of an AP are S₁, S₂ and S₃ respectively. Prove that S₃ = 3(S₂ – S₁). 
Solution. Let a be the first term and d the common difference of the AP   

Question. If the sum of m terms of an AP is the same as the sum of its n terms, show that the sum of its (m + n) terms is zero. 
Solution. Let a and d be the first term and the common difference of the given AP respectively.
Then, S_m = S_n 

Question. Find the sum of the AP: 7 + 10 , 1/2 + 14 + … + 84
Solution. Let a be the first term, d the common difference and an the last term of given AP. 

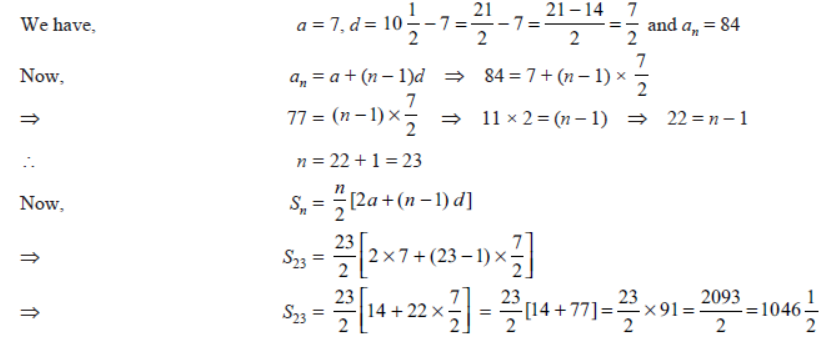
Question. The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference ‘d ’. 
Solution. We have, a = 5, Tn = 45, S_n = 400
∴ Tn = a + (n – 1)d
⇒ 45 = 5 + (n – 1)d ⇒ (n – 1)d = 40
S_n = n/2 (n + Tn)
⇒ 400 = n/2 (5 + 45) ⇒ n = 2 × 8 = 16
Substituting the value of n in (i), we get
(16 – 1)d = 40 ⇒ 15d = 40
d = 40/15 = 8/3

Question. The sum of the first n terms of an AP is given by S_n = 3n² – 4n. Determine the AP and the 12^th term.
Solution. We have, S_n = 3n² – 4n …(i)
Replacing n by n – 1, we get
Sn – 1 = 3 (n – 1)2 – 4 (n – 1) …(ii)
Since, an = S_n – S_n–1 = {3n² – 4n} – {3(n – 1)2 – 4(n – 1)}
= {3n² – 4n} – {3n² + 3 – 6n – 4n + 4}
= 3n² – 4n – 3n² – 3 + 6n + 4n – 4 = 6n – 7
So, nth term, an = 6n – 7 …(iii)
Substituting n = 1, 2, 3, … respectively in (iii), we get
a₁ = 6 × 1 – 7 = –1, a2 = 6 × 2 – 7 = 5
and a₃ = 6 × 3 – 7 = 11
Hence, AP is – 1, 5, 11, …
12^th term, a₁₂ = 6 × 12 – 7 = 72 – 7 = 65

Question. If the sum of the first p terms of an AP is ap² + bp, find its common difference. 
Solution. ap = Sp – Sp – 1 = (ap² + bp) – [a(p – 1)² + b(p – 1)]
= ap² + bp – (ap² + a – 2ap + bp – b)
= ap² + bp – ap² – a + 2ap – bp + b = 2ap + b – a
∴ a₁ = 2a + b – a = a + b
a₂ = 4a + b – a = 3a + b
⇒ d = a₂ – a₁ = (3a + b) – (a + b) = 2a

Question. If the mth term of an AP is 1/n and nth term is 1/m, then show that its (mn)^th term is 1.
Solution. Let a and d be the first term and the common difference of the AP respectively. 

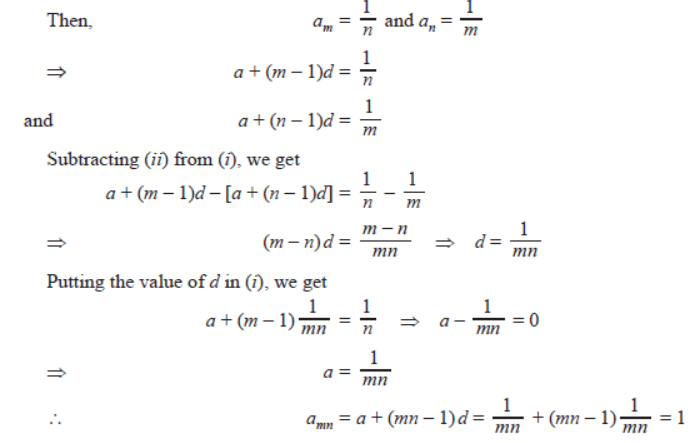
Assignments for Class 10 Mathematics Arithmetic Progression as per CBSE NCERT pattern

All students studying in Grade 10 Mathematics Arithmetic Progression should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Arithmetic Progression exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Arithmetic Progression which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.

Some advantages of Free Assignments for Class 10 Mathematics Arithmetic Progression

1. Solving Assignments for Mathematics Arithmetic Progression Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
2. By solving one assignments given in your class by Mathematics Arithmetic Progression teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
3. You will be able to understand the type of questions which are expected in your Mathematics Arithmetic Progression class test
4. You will be able to revise all topics given in the ebook for Class 10 Mathematics Arithmetic Progression as all questions have been provided in the question banks
5. NCERT Class 10 Mathematics Arithmetic Progression Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
6. Parents will be able to take print out of the assignments and give to their child easily.

All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Arithmetic Progression teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Arithmetic Progression Assignments PDF.