Assignments for Class 10 Mathematics Quadratic Equation have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Quadratic Equation from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Quadratic Equation. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Quadratic Equation book and get good marks in class 10 exams.
Short Answer type Questions :
Question. Solve the following quadratic equation for x: 4x2 + 4bx – (a2 – b2) = 0.
Solution. 4x2 + 4bx – (a2 – b2) = 0
Question. Solve the following quadratic equation for x: x2 – 2ax – (4b2 – a2) = 0.
Solution. x2 – 2ax – (4b2 – a2) = 0
Question. 2√3x2 – 5x + √3 = 0
Solution. √3 /2 , 1/√3
Question. 3x2 + 2√5x – 5 = 0
Solution. √5/3 , – √5
Question. 1/ x + 4 – 1/x – 7 = 11/30 , x ≠ – 4, 7
Solution. 2, 1
Question. Find the roots of quadratic equation: x2 − 3√5x +10 = 0
Solution.

Question. Write the discriminant of the quadratic equation (x + 5)2 = 2(5x –3).
Solution. (x + 5)2 = 2(5x – 3)
⇒ x2 + 25 + 10x = 10x – 6
⇒ x2 + 31 = 0
⇒ x2 + 0x + 31 = 0
∴ D = (0)2 – 4 × 1 × 31
= 0 – 124 = –124
Question. Solve the following quadratic equation for x: 9x2 – 6b2x – (a4 – b4) = 0.
Solution. 9x2 – 6b2x – (a4 – b4) = 0

Question. Find the roots of the equation ax2 + a = a2x + x.
Solution. a , 1/a
Question. Find the roots of quadratic equation: 5√5x2 + 30x + 8√5
Solution.
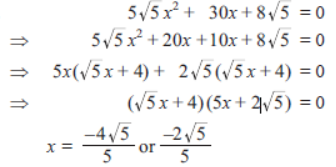
Question. Solve for x: x – 3/x – 4 + x – 5/ x – 6 = 10/6 ; x ≠ 4,6
Solution. 2 ± √10
Question. Solve for x: x – 2 /x – 3 + x – 4/x – 5 = 10/3 ; x ≠ 3 , 5
Solution. 7/2 , 6
Question. Solve for x: 4x2 – 4ax + (a2 – b2) = 0.
Solution.

Question. Two water taps together can fill a tank in 9 hours 36 minutes. The tap of large diameter takes 8 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution. Let x be the time taken by larger diameter tap.
∴ x + 8 be the time taken by smaller diameter tap.

x = 16 or x = – 4.8 (Rejected)
Hence, time taken by larger and smaller taps are 16 hrs
and 24 hrs respectively.
Question. Solve for x: 3(3x – 1/2x + 3) – 2 (2x + 3/3x – 1) = 5 ; x ≠ 1/3 , – 3/2
Solution. 0, –7
Question. The difference of squares of two numbers is 88. If the larger number is 5 less than twice the smaller number, then find the two numbers.
Solution. 9 and 13
Question. Solve the following quadratic equation for x: 4x2 – 4a2x + (a4 – b4) = 0.
Solution. 4x2 – 4a2x + (a4 – b4) = 0


Question. Find the discriminant of the quadratic equation: 4x2 – 2/3x – 1/16 = 0
Solution. 3328
Question. Sum of the areas of two squares is 544 m2. If the difference of their perimeters is 32 m, find the sides of the two squares.
Solution. Let the sides of two squares in metres be x and y respectively (where x > y).
Given:
Sum of areas of two squares = 544 m2
⇒ x2 + y2 = 544 …(i)
Also, difference of their perimeters
= 32 m
⇒ 4x – 4y = 32
⇒ x – y = 8
⇒ y = x – 8 …(ii) (1)
Substituting the value of y for equation (ii) in equation (i),
we get
x2 + (x – 8)2 = 544
⇒ x2 + x2 – 16x + 64 – 544 = 0
⇒ 2x2 – 16x – 480 = 0
⇒ x2 – 8x – 240 = 0

Question. A rectangular field is 20 m long and 14 m wide. There is a path of equal width all around it, having an area of 111 sq m. Find the width of the path.
Solution. 1.5 m
Question. At ‘t’ minutes past 2 pm, the time needed by the minute hand of a clock to show 3 pm was found to be 3 minutes less than t2/4 minutes. Find t.
Solution. 14 minutes
Question. Find a natural number whose square diminished by 84 is equal to thrice of 8 more than the given number.
Solution.

Question. Solve for x: √3x2 + 14x – 5√3 = 0
Solution.

Question. Find the roots of the equation x2 + 7x + 10 = 0.
Solution. x2 + 7x + 10 = 0
x2 + 5x + 2x + 10 = 0 (½)
(x + 5)(x + 2) = 0
x = –5, x = –2
Question. Solve for x: 4√3x2 + 5x – 2√3 = 0
Solution. Consider
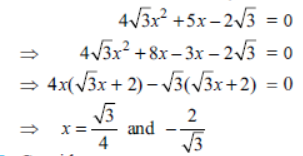
Question. Solve for x: x2 x – (√2 + 1) x + √2 = 0
Solution. Consider:

Question. Solve for x: 1/ x – 3 – 1/x + 5 = 1/6 , x ≠ 3, – 5.
Solution.

Question. Solve the quadratic equation 2x2 + ax – a2 = 0 for x using quadratic formula.
Solution. 2x2 + ax – a2 = 0
Here, a = 2, b = a and c = –a2.
Using the formula,

Question. Solve the following quadratic equation:
9x2 – 9 (a + b) x + [2a2 + 5ab + 2b2] = 0
Solution. We have 9x2 – 9 (a + b) x + [2a2 + 5ab + 2b2] = 0
Here, A = 9, B = –9 (a + b) and C = [2a2 + 5ab + 2b2]
So, discriminant,
D = B2 – 4 AC = { –9 (a + b)}2 – 4 × 9 (2a2 + 5 ab + 2b2)
= 92 (a + b)2 – 4 × 9 (2a2 + 5ab + 2b2)
= 9 {9 (a + b)2 – 4 (2a2 + 5 ab + 2b2 )}
= 9 {9a2 + 9b2 + 18ab – 8a2 – 20ab – 8b2}
= 9 (a2 + b2 – 2ab) = 9 (a – b)

Question. Find the solution of the quadratic equations by quadratic formula.

Solution.

Question. Using the quadratic formula, solve the equation
a2b2x2 – (4b4 – 3a4) x – 12a2b2 = 0
Solution. Comparing given equation with Ax2 + Bx + C = 0, we get
A = a2b2, B = –(4b4 – 3a4) and C = –12a2b2.
∴ B2 – 4AC = (4b4 – 3a4)2 – 4 × a2b2 × (–12a2b2)
= 16b8 + 9a8 – 24a4b4 + 48a4b4
= 16b8 + 9a8 + 24a4b4 = (4b4 + 3a4)2

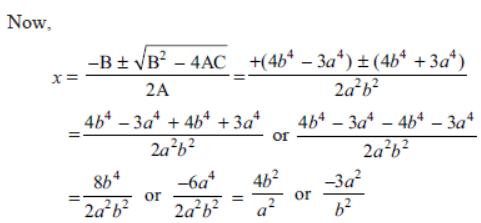
Question. Two water taps together can fill a tank in 6 hours. The tap of larger diameter takes 9 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution. 9 hrs.
Question. Two pipes running together can fill a tank in 11 ,1/9 minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately .
Solution. 20 minutes, 25 minutes.
Question. The difference of two natural numbers is 3 and the difference of their reciprocals is 3/28 . Find the numbers.
Solution. 4, 7
Question. √3x2 + 10x + 7√3 = 0
Solution. -√3 , -7/√3
Question. Solve for x: x + 1 /x – 1 + x – 2/x + 2 = 4 – 2x + 3/x – 2 ; x ≠ 1 , -2 , 2 .
Solution.

Question. (x – 3)(2x + 3) = 0
Solution. 3, -3/2
Question. A pole has to be erected at a point on the boundary of a circular park of diameter 17 m in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Find the distances from the two gates where the pole is to be erected.
Solution. Let P be the position of the pole.
∠APB = 90° (angle in a semicircle)

Question. 3x2 – 2ax – a2 = 0
Solution. a , -a/3
Question. At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha.
Solution. Nisha’s age = 5 years, Asha’s age = 27 years
Question. The difference of two natural numbers is 5 and the difference of their reciprocals is 5/14 . Find the numbers.
Solution. 7, 2
Question. Solve the equation for x: 3x – 4 / 7 + 7/3x – 4 = 5/2 , x ≠ 4/3 .
Solution.

Question. Find two consecutive positive integers sum of whose squares is 365.
Solution. Let two consecutive positive integers be x and x + 1
∴ x2 + (x + 1)2 = 365
⇒ x2 + x − 182 = 0
(x + 14)(x − 13) = 0
∴ x = 13
Hence, two consecutive positive integers are 13 and 14.
Question. A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr more than its original speed. If it takes 3 hours to complete total journey, what is the original average speed?
Solution. Let the original average speed of train be x km/hr.

Question. 3a2x2 + 8abx + 4b2 = 0
Solution. – 2b/a , – 2b/3a
Question. Some students planned a picnic. The total budget for food was ₹ 2,000. But 5 students failed to attend the picnic and thus the cost of food for each member increased by ₹ 20. How many students attended the picnic and how much did each student pay for the food?
Solution. Case I. Let number of students = x
and cost of food for each member = ₹ y
Then x × y = 2,000 …(i)(1)
Case II. New number of students = x – 5
New cost of food for each member = ₹ (y + 20)
Then (x – 5)(y + 20) = 2,000
fi xy + 20x – 5y – 100 = 2,000 …(ii)(1)
Solving (i) and (ii), we get
∴ x = –20, 25 (1)
x = –20 is rejected because number of students can’t be
negative.
So, x = 25
∴ y = 80
Number of students = 25
Cost of food for each student = ₹ 80.
Question. Solve the equation for x: 1/x + 1 + 2/x+2 = 5/x +4 , x ≠ -1 , -2 , -4 .
Solution. Given that:
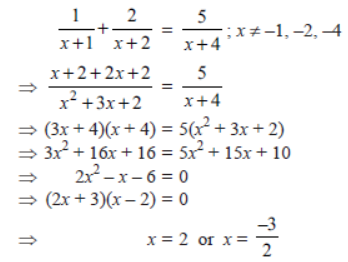
Question. A two-digit number is such that the product of its digits is 14. When 45 is added to the number, the digits interchange their places. Find the number.
Solution. 27
Question. A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution. 6 km/h.
Question. Solve for x: √2x + 9 + x = 13.
Solution.

Question. In a flight of 600 km, an aircraft was slowed down due to bad weather. The average speed of the trip was reduced by 200 km/hr and the time of flight increased by 30 minutes. Find the duration of flight.
Solution. 1 hr
Question. Solve for x: √6x + 7 − (2x − 7) = 0.
Solution.

Question. A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m. Find the length and breadth of the park.
Solution. Let ABCD is a rectangular park and CDE is a triangular park (isosceles triangle).

Question. Solve for x: √3x2 – 2√2x – 2√3 = 0
Solution.
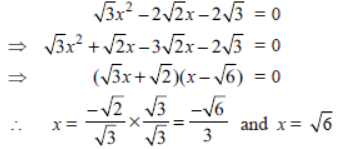
Question. Solve the following equation: 1//x – 1/x – 2 = 3 , x ≠ 0, 2 .
Solution.

Quadratic Equation : a polynomial of second degree is called quadratic equation.
ax2 +bx +c,a≠0
Methods for solving quadratic equation
- Factorization method
- Completing the square
- Quadratic formula
- Foots of quadratic equation ax2 +bx +c=0 are

Nature of roots :
- Two distinct real roots, if b2– 4ac >0,
- Two equal real roots, if b2-4ac=0 and each root is b/2a
- No real roots, ifif b2– 4ac < 0.if b2– 4ac is called discriminant of the quadratic equation and denoted by D.
- A quadratic polynomial whose zeroes are α,β is given by p(x) = x2 =(α + β)x + αβ =x2-( sum of the zeroes)x+product of the zeroes
Cubic polynomial whose zeroes are α,β,γ is given by p(x) = x3 -(α + β +γ)x2 +( αβ + βγ + αγ)x – α β γ = x3 -( sum of the zeroes)x2 +( sum of the products of the zeroes taken two at a time)-product of the zeroes
Question. Find the value/s of k for which the quadratic equation 3x2 + kx + 3 = 0 has real and equal roots.
Solution. Given, quadratic equation is: 3x2 + kx + 3 = 0
For real and equal roots b2 – 4ac = 0
Here, a = 3, b = k and c = 3
⇒ b2 – 4ac = (k)2 – 4 × 3 × 3 = 0
⇒ k2 = 36
⇒ k = ± 6
Hence, the value of k is –6.
Question. Solve for x :
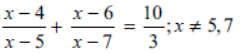
Solution.
Question. The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
Solution. Let the two consecutive odd numbers be x and x + 2.
∴ x2 + (x + 2)2 = 394 ⇒ x2 + x2 + 4 + 4x = 394
⇒ 2x2 + 4x + 4 = 394 ⇒ 2x2 + 4x – 390 = 0
⇒ x2 + 2x – 195 = 0 ⇒ x2 + 15x – 13x – 195 = 0
⇒ x (x + 15) – 13 (x + 15) = 0 ⇒ (x – 13) (x + 15) = 0
Either x – 13 = 0 or x + 15 = 0 ⇒ x = 13 or x = – 15 (neglected)
When first number x = 13, then second number x + 2 = 13 + 2 = 15.
Question. Two pipes running together can fill a cistern in 3,1/13 hours. If one pipe takes 3 hours more than the other to fill it, find the time in which each pipe would fill the cistern.
Solution. Let time taken by faster pipe to fill the cistern be x hrs.
Therefore, time taken by slower pipe to fill the cistern = (x + 3) hrs
Since the faster pipe takes x minutes to fill the cistern.
∴ Portion of the cistern filled by the faster pipe in one hour = 1/x
Portion of the cistern filled by the slower pipe in one hour = 1/x + 3
Portion of the cistern filled by the two pipes together in one hour = 1/40/30 = 13/40

Question. The sum of two numbers is 15 and the sum of their reciprocals is 3/10 . Find the numbers.
Solution. Let the numbers be x and 15 – x.
According to given condition,

Question. Solve the following quadratic equations by the factorisation method.
(a) 7x2 = 8 – 10x (b) x (x + 9) = 52
(c) 3 (x2 – 4) = 5x (d) x (x + 1) + (x + 2) (x + 3) = 42
Solution. (a) 7×2 = 8 – 10x ⇒ 7x2 + 10x – 8 = 0
⇒ 7x2 + 14x – 4x – 8 = 0 ⇒ 7x(x + 2) – 4 (x + 2) = 0
⇒ (7x – 4) (x + 2) = 0

Question. Solve for x:
Solution.

Question. If Zeba was younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than five times her actual age. What is her age now?
Solution. Let the present age of Zeba be x years.
Age before 5 years = (x – 5) years
According to given condition,
(x – 5)2 = 5x + 11
⇒ x2 + 25 – 10x = 5x + 11 ⇒ x2 – 10x – 5x + 25 – 11 = 0
⇒ x2 – 15x + 14 = 0 ⇒ x2 – 14x – x + 14 = 0
⇒ x (x – 14) – 1 (x – 14) = 0 ⇒ (x – 1) (x – 14) = 0
⇒ x – 1 = 0 or x – 14 = 0
⇒ x = 1 or x = 14
But present age cannot be 1 year.
∴ Present age of Zeba is 14 years.
Question. Solve the equation

Solution.

Question. Solve for x:
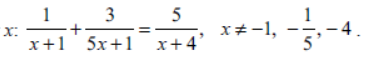
Solution. Here,

Question. The difference of two natural numbers is 5 and the difference of their reciprocals is 1/10 . Find the numbers.
Solution. Let the two natural numbers be x and y such that x > y.
According to the question,
Difference of numbers, x – y = 5 ⇒ x = 5 + y …(i)
Difference of their reciprocals,

Question. Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream.
Solution. Let the speed of stream be x km/hr.
∴ Speed of boat in upstream = (15 – x) km/hr.
Speed of boat in downstream = (15 + x) km/hr.

Question. A train travelling at a uniform speed for 360 km would have taken 48 minutes less to travel the same distance if its speed were 5 km/hour more. Find the original speed of the train.
Solution. Let original speed of the train be x km/hr.
Time taken at original speed = 360/x hours

Question. A plane left 30 minutes late than its scheduled time and in order to reach the destination 1500 km away in time, it had to increase its speed by 100 km/h from the usual speed. Find its usual speed.
Solution. Let the usual speed of the plane be x km/hr.
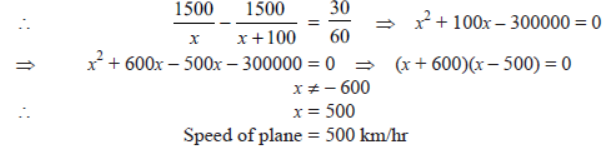
Question. In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2. Find the length and breadth of the pond.
Solution. Let ABCD be a rectangular lawn and EFGH be rectangular pond. Let x m be the width of grass area, same around the pond.
Now, length of lawn = 50 m, width of lawn = 40 m
∴ Length of pond = (50 – 2x) m, width of pond = (40 – 2x) m
Since area of grass surrounds the pond = 1184 m2
⇒ Area of lawn – Area of pond = 1184 m2
⇒ 50 × 40 – (50 – 2x) (40 – 2x) = 1184
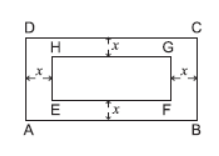
⇒ 2000 – (2000 – 80x – 100x + 4x2) = 1184
⇒ 4x2 – 180 x + 1184 = 0 or x2 – 45x + 296 = 0 fi x2 – 37x – 8x + 296 = 0
⇒ (x – 37) (x – 8) = 0 fi x = 37, 8
Since x = 37 is not possible, as otherwise the length of pond will be negative.
Hence, x = 8 is the required solution.
∴ Length of pond = 50 – 2 × 8 = 34 m
and breadth of pond = 40 – 2 × 8 = 24 m
Question. For what values of k does the quadratic equation 4x2 – 12x – k = 0 have no real roots ?
Solution. Given equation is: 4x2 – 12x – k = 0
For equation to have no real roots, D < 0
or b2 – 4ac < 0
Here, a = 4, b = – 12, c = – k
(– 12)2 – 4 × 4 × (– k) < 0
144 + 16k < 0
16k < –144
k < –9
Hence, the value of k should be less than – 9.
Question. Find the nature of the roots of the quadratic equation 2x2 – 4x + 3 = 0.
Solution. Given: quadratic equation :
2x2 – 4x + 3 = 0
Here, a = 2, b = – 4, c = 3
Discriminant, D = b2 – 4ac
= (– 4)2 – 4 × 2 × 3
= 16 – 24 = – 8 < 0
∴ D < 0
Hence, the given equation does not have real roots.
PRACTICE EXERCISE
Question. 25x2 – 10 x – 8 = 0
Solution. 4/5 , -2 /5
Question. x2 – 3x – 28 = 0
Solution. 7, –4
Question. 3x2 + 12ax – a2 = 0, where a is real.
Solution. – a , a/3
Question. 5x2 + 16x = – 12
Solution. – 2 , 6/5
Question. 6 √2x2 + 5x – 3 √2 = 0
Solution. √2/3 , – 3/2√2
Question. 6a2x2 – 7abx – 3b2 = 0
Solution. – b /3a , 3b/2a
Question. x2 – (√3 +1)x + √3 = 0
Solution. 1, √3
Question. 4x2 + 3x + 9 = 0
Solution. No real roots
Question. 4x2 + 4 √3 x + 3 = 0
Solution. – √3/2 , – √3/2
Question. – 8x2 +10x = 3
Solution. 3/4 , 1/2
Question. 15x2 – 28 = x
Solution. 7/5 , -4/3
Question. x2 – 2ax + a2 – b2 = 0
Solution. a – b, a + b
Question. 4x2 – 4a2x + (a4 – b4 ) = 0
Solution. a2 + b2 /2 , a2 – b2 /2
Question. If x = 5 and x = 5/4 are the roots of the equation ax2 – 15x + b = 0. Find the value of a and b.
Solution. a = 4, b = – 25
Question. Determine whether x = 1/2 and x = 3/2 are solutions of the equation 2x2 -5x +3 = 0 or not.
Solution. x =1/2 is not a solution, but x = 3/2 is a solution.
Question. 3x2 – 5x + 2 = 0
Solution. 1, 2/3
Question. a2b2x2 + b2x – a2x +1 = 0
Solution. -1/a2 , 1/b2
Question. 1/ a + b + x = 1/a + 1/b + 1/x , a + b ≠ 0
Solution. –a, –b
Question. x + 3 / x – 2 – 1 – x/x = 17/4
Solution. 4 , -2/9
Question. x – 1 /2x – 1 + 2x + 1 /x – 1 = 5/2 ; x ≠ – 1/2,1
Solution. –1
Question. x – 1 /x – 2 + x – 3 / x – 4 = 3 , 1/3 ; x ≠ 2,4
Solution. 5 , 5/2
Question. x2 – 8x = 0
Solution. 0, 8
Question. 2x2 + x – 4 = 0
Solution. – + √33 / 2 , -1- √33 / 4
Question. 9x2 – 15x + 6 = 0
Solution. 1,2/3
Question. x2 – 6 √2x + 10 = 0
Solution. √2,5 √2
Question. x2 – (√2 +1)x + √2 = 0
Solution. √2, 1
Question. a2x2 – 3abx + 2b2 = 0
Solution. 2b/a , b/a
Question. 3x2 – 5x +2 = 0
Solution. 1
Question. Which of the following are quadratic equations ?
(a) x2 + 7x – 12 = 0 (b) 9x2 – 12 x = 0 (c) x – 4/x = x2
(d) 7x2 = 0 (e) x2 + 1/x2 = 4 (f) x(x + 7) = x2 – 4x + 2
Solution. (a), (b), (d)
Question. In each of the following, determine whether the given values are the solutions of the given quadratic equations or not :
(a) x2 – 5x + 6 = 0 ; x = 2, x = 3 (b) 7×2 + 4x – 20 = 0; x = – 2 , x = – 10/7 (c) x + 1/x = 25/12 ; x = 2/3 , x = 3/4 (d) x2 – 2 √3 – 9 = 0 ; x = – 3, x = 3 √3
(e) √3 x2 + 11 x + 6√3 = 0 ; x = – 2/√3 , x = – 3√3
Solution. (a) x = 2 and x = 3 are solutions.
(b) x = – 2 is a solution, but x = – 10/7 is not a solution.
(c) x = 2/3 is not a solution, x = 3/4 is a solution.
(d) x = – √3 and x = 3 √3 are solutions.
(e) x = -2/√3 and x = =3 √3 are solutoins.
Question. –4x2 = 6 – 3x
Solution. –87
Question. x2 – 9x + 20 = 0
Solution. 4, 5
Question. x2 – 6x + 9 = 0
Solution. 3, 3
Question. x2 – 2xb + b2 = 0
Solution. b, b
Question. x2 – 4x + 4 = (3/2)2
Solution. 7/2 , 1/2
Question. 3x2 + 2 √5x – 5 = 0
Solution. -√5 , √5/3
Question. √5x2 + 9x -14 √5 = 0
Solution. √5 , -14/√5
Question. 2x2 – (q + 2 p)x + pq = 0
Solution. p , q/2
Question. 3y2 + (6 + 4a) y + 8a = 0
Solution. – 2, -4a/3
Question. a/x – b + b/x – a = 2 ; x ≠ a , b
Solution. a + b , a + b /2
Question. 4x2 – 2 (a2 + b2) x + a2b2 = 0
Solution. a2 /2 , b2/2
Question. (k + 4)x2 + (k + 1)x + 1 = 0
Solution. k = 0 or 3
Question. 5x2 – 6x + p = 0
Solution. p ≤ 9/5
Question. abx2 – (a + b)2 (x – 1) = 0
Solution. a + b /2 , a + b /a
Question. 9x2 – 9(a + b)x + (2a2 + 5ab + 2b2) = 0
Solution. 2a + b /3 , a + 2b/3
Question. abx2 + (b2 – ac)x – bc = 0
Solution. – b/a , c/b
Question. x2 + x(a + 2) + (a +1) = 0
Solution. –1, –(1 + a)
Question. 4/x – 3 = 5/2x + 3 ; x ≠ 0 , – 3/2
Solution. –2, 1
Question. p2 x2 + ( p2 – q2 )x – q2 = 0
Solution. – 1, q2/p2
Question. 1/ x + 1 + 2/x + 2 = 4/x + 4 ; x ≠ 1 , 2, 4
Solution. 2 ± 2 √3
Question. 6x2 + (12 – 8a)x -16a – 0
Solution. – 2 , 4a/3
Question. 2x – 3 /x – 2 + 2x – 7/x – 4 = 16/3 ; x ≠ 2,4
Solution. 5, 5/2
Question. x -a/x – b + x – b /x -a = a/b + b/a ; x ≠ a,b
Solution. 0, a + b
Question. In each of the following, find the value of p for which the given value is a solution of the given equation:
(a) (2 p +1)x2 + 2x – 3 = 0; x = 2 (b) x2 + 2ax – 2 p = 0; x = -a
(c) x2 – x(a + b) + p = 0; x = b (d) px2 – √2x – 4 = 0; x = √2
Solution. (a) p = -5/8 (b) p = – a2/2 (c) p = ab (d) p = 3
Question. 5x2 + 4x – 1 = 0
Solution. 36
Question. x2 + 2ax + 3b = 0
Solution. 4a2 – 12b
Question. √2x2 – 3x – 3 √2 = 0
Solution. 33
Question. 9x2 – 6x + 1 = 0
Solution. Real and equal
Question. x2 + x – 12 = 0
Solution. Real and unequal
Question. 4√3x2 + 5x + 2 √3 = 0
Solution. no real roots
Question. 4x2 – 4x + 1 = 0
Solution. Real and equal
Question. (x – 2a) (x – 2b) = 4ab
Solution. Real and unequal
Question. 9x2 – 5 px + 1 = 0
Solution. p ≥ 6/5 or p ≤ – 6/5
Question. x2 + 4x + p = 0
Solution. p ≤ 4
Question. 2x2 + px + 2 = 0
Solution. p ≤ – 4 or p ≥ 4
Question. 4x2 – 3px + 1 = 0
Solution. p ≤ – 4/3 or p ≥ 4/3
Question. For what value of k, (4 – k) x2+ (2k + 4)x + (8k + 1) = 0, is a perfect square.
Solution. k = 0, 3
Question. 2x2 – 10x + k = 0
Solution. k = 25/2
Question. kx2 – 2 √5 x + 4 = 0
Solution. k = 5/2
Question. (k + 4)x2 + (k + 1)x + 1 = 0
Solution. k = – 3 or 5
Question. k 2 x2 – 2(2k -1)x + 4 = 0
Solution. k = 1/4
Question. Is 0.2 a root of the equation x2 – 0.4 = 0?
Solution. No, because 0.2 does not satisfy the quadratic equation i.e.
x2 – 0.4 = (0.2)2 – 0.4
= 0.04 – 0.4
= -0.36 ≠ 0
Question. Find the Value of K if the equation x2- 2(k+1)x + k2 = 0 has equal roots.
Solution. ± 1
Question. Find the roots of x2– 3x -10 = 0
Solution. -2 and 5
Question. A two digit number is such that the product of its digit is 35.When18 is added to the number, the digits interchange the places. Find the number.
Solution. 57
Question. Solve 3x2-23x-110 = 0
Solution. -10/3, 11
Question. Solve the following equation for ‘x’, 9x2-9(a+b)x+2a2+5ab+2b2 = 0
Solution. a + b/3 , 2(a + b)/3
Question. The product of two consecutive odd numbers is 483.Find the numbers.
Solution. 21,23
Question. If the x = 2 and x = 3 are roots of the equation 3x2 + 2 kx − 2m = 0, find the value of k and m.
Solution. m = 9 and k=-15/2
Question. Solve the equation: x/x + 1 + x + 1/x = 34/15x ≠ 0; x ≠ -1 .
Solution. 3/2 or -5
Question. Solve the equation 2x2 – 5 x + 3= 0 by the method of completing the square.
Solution. 3/2 or 1
Question. Using quadratic formula, solve the equation: p2x2 + (p2– q2)x – q2 = 0
Solution. q2/p2 or -1
Question. 300 apples are distributed equally among a certain number of student’s .Had there been 10 more Students, each would have received one apple less. Find the number of students.
Solution. 50
Question. Find the roots of Quadratic equation 16x2–24x –1= 0 by using the quadratic formula.
Solution. 3 ± √10/4
Question. Find the Discriminant of the Quadratic equation 2x2-4x+3=0and hence find the nature of its roots.
Solution. -8, and roots are not real.
Question. In a class test ,the sum of Shefali‘s marks in math’s and English is 30.Had she got2 marks more in math’s and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
Solution. (Marks in math’s=12, marks in English=18) or (marks in math’s=13, marks in English=17)
Question. Represent the situation in the form of Quadratic equation:
The Product of Rahman’s age (in years) 5 years ago with his age 9 years later is 15.
Solution. x2+4x-60 =0
Question. A person on tour hasRs.360 for his daily expenses. If he exceeds his tour Programme by four days, he must cut down his daily expenses, by Rs 3 per day. Find the number of days of his tour Programme.
Solution. 20 days.
Question. Find the value of ‘p’ so that the equation 3x2 – 5x – 2p = 0has equal roots. Also find the roots.
Solution. 25/24
Question. The sum of two numbers is 15. If the sum of their reciprocals is 3/10 . Find the two numbers.
Solution. (10,5)or(5,10)
Question. Find the quadratic equation whose roots are 2 + √3and2 − √3.
Solution. x2-4x +1=0
Question. For what value of k, x = a is a solution of equation x2 -(a+b)x+k=0?
Solution. K=ab
Question. Find the values of K for which the .equation 9x2 + 2kx +1 = 0 have real roots.
Solution. -3≤ k ≤ 3
Question. Divide 29 intotwopartssothatthesumofsquaresofthepartsis 425.
Solution. (13,16) or (16,13)
Question. If D > 0,then write the roots of a quadratic equation ax2+bx+c = 0
Solution. -b ± √b2 – 4ac/2a
Question. Find the Discriminant of x2+ 5x+ 5 = 0.
Solution. 5
Question. Find the sum of roots of a quadratic equation x2 + 4x- 32 = 0
Solution. -4
Question. Find the product of the roots of the quadratic equation 2x2 + 7x – 4 = 0
Solution. – 2
Question. If the equation (1 +m2)x2 – 2mcx – c2 – a2 = 0 has equal roots. Show that c2 = a2(1 + m2).
Solution. Rs 58 per litre
Question. If the price of petrol is increased by Rs.2 per litre,a person had to buy1 litre less petrol for Rs.1740. Find the Original price of the petrol at that time.
a) Why do you think the price of petrol is increasing day by day?
b) What should we do to save petrol?
Solution. Yes,l=20mandb=20m.
Question. Solve for x: 9a2 – 6ax – (a2 – b2) = 0
Solution. (a+b)/3 and (a- b)/3
Short Answer Type Questions
Question. If x = − 1/2 is a solution of the quadratic equation 3x2 + 2kx – 3 = 0, find the value of k.

Question. Find the value of k for which x = 3 is a solution of the equation kx2 x + √3 − 4 = 0.
Solution.

Question.. A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. We would like to find out the number of toys produced on that day.
Solution. x2 – 55x + 750 = 0
Question.. If one root of the quadratic equation 3x2 + px + 4 = 0 is 2/3 , then find the value of p and the other root of the equation.
8. 3x2 + px + 4 = 0
3(2/3)2 + P(2/3) + 4 = 0
4/3 + 2P/3 + 4 = 0 (½)
p = –8 (½)
3x2 – 8x + 4 = 0
3x2 – 6x – 2x + 4 = 0 (½)
x = 2/3 or x = 2 (½)
Hence, x = 2 (½)
Question.. If x = 2/3 and x = –3 are roots of the quadratic equations ax2 + 7x + b = 0, find the values of a and b.
Solution.
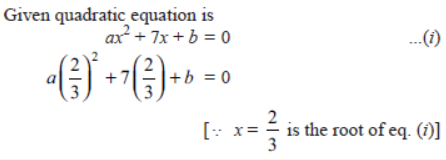
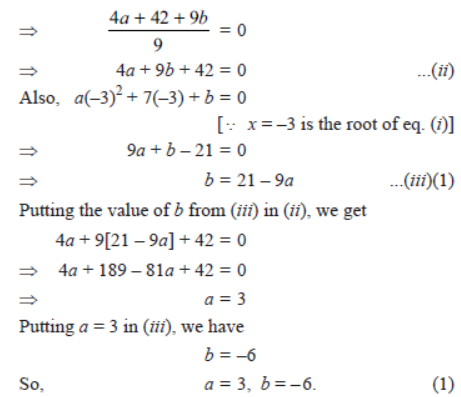
Question.. John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they have now is 124. We would like to find out how many marbles they had to start with.
Solution. x2 – 45x + 324 = 0
Question. Solve the given quadratic equation for x: 9x2 – 9(a + b)x + (2a2 + 5ab + 2b2) = 0
Solution. 9x2 – 9(a + b)x + (2a2 + 5ab + 2b2) = 0
On comparing the given equation with
ax2 + bx + c = 0, we get :
a = 9, b = – 9(a + b), c = 2a2 + 5ab + 2b2
Discriminant,
D = b2 – 4ac
= [– 9(a + b)]2 – 4 × 9(2a2 + 5ab + 2b2)
= 81(a + b)2 – 36(2a2 + 5ab + 2b2)
= 81(a2 + b2 + 2ab) – 72a2 – 180ab – 72b2
= 81a2 + 81b2 + 162ab – 72a2 – 180ab – 72b2
= 9a2 + 9b2 – 18ab
= 9(a2 + b2 – 2ab)
= 9(a – b)2 = [3(a – b)]2
Then, roots : x = – b ± √D /2a

Question. For what values of k, the roots of the equation x2 + 4x + k = 0 are real?
Solution. Since, the roots of the equation x2 + 4x + k = 0 are real,
i.e. D ≥ 0
b2 – 4ac ≥ 0
Here, a = 1, b = 4, c = k
⇒ (4)2 – 4 × 1 × k ≥ 0
⇒ 16 – 4k ≥ 0
⇒ k ≤ 4
Hence, the value of ‘k’ is less than or equal to 4.
Question. If x = 2 and m = 3, the equation is 3x2 – 2kx + 2m = 0, find k.
Solution. 3x2 – 2kx + 2m = 0
x = 2 and m = 3 [Given]
So, 3(2)2 – 2k(2) + 2(3) = 0
⇒ 12 – 4k + 6 = 0
⇒ – 4k + 18 = 0
⇒ k = 9/ 2.
Question. If one root of the quadratic equation 6x2 – x – k = 0 is 2/ 3 , then find the value of ‘k’.
Solution. Given: quadratic equation: 6x2 – x – k= 0.
Its one of its root: 2/ 3
If x = 2/3 is root of the given equation, then it
will satisfy the given equation:
Then, 6 (2/3)2 – 2/3 – k = 0
⇒ 6 x 4/ 9 – 2/ 2 – k = 0
⇒ 8/3 – 2/3 – k = 0
⇒ k = 2
Hence, the value of k is 2.
Question. For what values of ‘a’, does the quadratic equation x2 – ax + 1 = 0 not have real roots?
Solution. Given quadratic equation is x2 – ax + 1 = 0
On comparing the given equation with
Ax2 + Bx + C = 0, we get:
A = 1, B = – a, C = 1
For real roots, D > 0
B2 – 4AC > 0
i.e. (– a)2 – 4 × 1 × 1 = 0
a2 > 4
or a > √4
or – 2 > a > 2
Hence, the value of ‘a’ lies between – 2 and 2.
Question. Find the values of ‘k’ for which x = 2 is a solution of the equation kx2 + 2x – 3 = 0.
Solution. Given equation is, kx2 + 2x – 3 = 0
if x = 2, then
⇒ k (2)2 + 2 (2) – 3 = 0
⇒ 4k = – 1
⇒ k = 1/4
Hence, the value of k is =1/4
Question. If x = 3 is one root of the quadratic equation x2 – 2kx – 6 = 0, then find the value of k.
Solution.

Question. A line segment AB of length 2m is divided at a point C into two parts such that AC2 = AB × CB. Find the length of CB.
Solution. Let the length of AC be x
The, BC = 2 – x
AC2 = AB × CB (given)
∴ x2 = 2 × (2 – x)
[∵ AB = 2m (given)]
⇒ x2 = 4 – 2x
⇒ x2 + 2x – 4 = 0
Now, if we compare the above equation
with ax2 + bx + c = 0.
Then, a = 1, b = 2, c = –4
Root of the equation are,
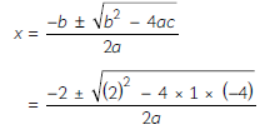

Question. Find the value of k for which the roots of the quadratic equation 2x2 + kx + 8 = 0 will have equal value.
Solution. Given: quadratic equation is 2x2 + kx + 8 = 0
For roots of the equation to be equal.
D = 0
i.e., b2 – 4ac = 0
Here, a = 2, b = k and c = 8
⇒ k2 – 4 × 2 × 8 = 0
⇒ k2 = 64
⇒ k = ± 8
Hence, the value of k is 8 or – 8.
Question. Show that if the roots of the following quadratic equation are equal, then ad = bc x2(a2 + b2) + 2(ac + bd)x + (c2 + d2) = 0
Solution. Given, quadratic equation is :
x2(a2 + b2) + 2(ac + bd)x + (c2 + d2) = 0
whose roots are equal.
To Prove : ad = bc
Proof : In the given equation,
A = a2 + b2
B = 2(ac + bd)
C = c2 + d2
Since, roots of the given equation are equal.
∴ Discriminant B2 – 4AC = 0
[2(ac + bd)]2 – 4 × (a2 + b2) (c2 + d2) = 0
⇒ 4(ac + bd)2 – 4(a2c2 + b2c2 + a2d2 + b2d2) =0
⇒ 4(a2c2 + b2d2 + 2abcd) – 4a2c2 – 4b2c2
– 4a2d2 – 4b2d2 = 0
⇒8abcd – 4a2d2 – 4b2c2 = 0
⇒ a2.b2 + b2c2 – 2abcd = 0
⇒ (ad – bc)2 = 0
On taking square-root on both sides
⇒ ad – bc = 0
⇒ ad = bc
Hence, proved.
Question. For what positive values of k, does the quadratic equation 3x2 – kx + 3 = 0 not have real roots ?
Solution. Given: quadratic equation 3x2 – kx + 3 = 0, has no real roots.
On comparing the given equation with ax2 + bx
+ c = 0, we have:
a = 3, b = – k, c = 3
Then, discriminant,
D = b2 – 4ac
= (– k)2 – 4 × 3 × 3
= k2 – 36
But for no real roots, D < O
Then k2 – 36 < 0
⇒ k2 < 36
⇒ k < ± 6
⇒ k > – 6 or k < 6
Hence, the value of k < 6 (positive value) for no real roots.
Question. Solve for x : 8x2 – 2x – 3 = 0
Solution. 8x2 – 2x – 3 = 0
⇒ 8x2 – 6x + 4x – 3 = 0
⇒ 2x(4x – 3) + 1(4x – 3) = 0
⇒ (4x – 3) (2x + 1) = 0
⇒ 4x – 3 = 0 or 2x + 1 = 0
i.e., x = 3 4 or -1/ 2
Question. Solve the following quadratic equation :
6a2x2 – 7abx – 3b2 = 0
Solution. Given: quadratic equation is :
6a2x2 – 7abx – 3b2 = 0
On comparing the given equation with
AX2 + BX + C = 0, we get:
A = 6a2, B = –7ab, C = –3b2
Then, discrimnants.
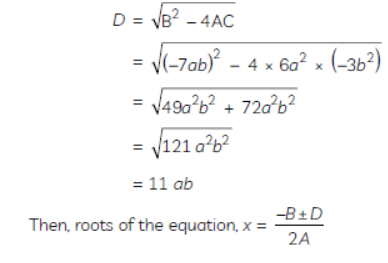

Question. Solve for x : 1/ x + 4 – 1/ x – 7 = 11/ 30 , x# – 4 , 7 .
Solution. Solve for x : 1/ x + 4 – 1/ x – 7 = 11/ 30
Now 1/ x + 4 – 1/ x – 7 = 11/ 30
⇒ x – 7 – x – 4 / (x +4) (x -7) = 11 / 30
⇒ (x + 4) (x – 7) + 30 = 0
⇒ x2 – 3x + 2 = 0
⇒ (x – 2) (x – 1) = 0
i.e. x – 1 = 0 or x – 2 = 0
⇒ x = 1 or 2
Question. Solve for x : √3x2 + 10x – 8√3 = 0
Solution. Given: 3x2 + 10x − 8 3 = 0
On comparing the above equation with ax2 + bx + c = 0,
we get : a = √3 , b = 10 and c = – 8√3
Then, discriminant, D = b2 – 4ac
= (10)2 – 4 × √3 × ( – 8√3 )
= 100 + 96
= 196
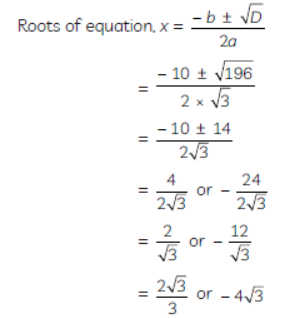
Hence, the roots of the given equation are 2 √3/3 and – 4 √3.
Question. A quadratic equation with integral coefficient has integral roots. Justify your answer.
Solution. No, the given statement is not always true.
Consider the quadratic equation
8x2 – 2x – 1 = 0
By splitting the middle term,
8x2 – 4x + 2x – 1 = 0
4x(2x – 1) + 1(2x – 1) = 0
(4x + 1)(2x – 1) = 0
If 4x + 1 = 0 ⇒ x = –1/4
2x – 1 = 0 ⇒ x = 1/2
So, the given equation has integral coefficients but no integral roots.
Hence, the given statement is false.
Question. Solve for x : 6x2 + 11x + 3 = 0
Solution. 6x2 + 11x + 3 = 0
⇒ 6x2 + 9x + 2x + 3 = 0
⇒ 3x (2x + 3) + 1 (2x + 3) = 0
⇒ (2x + 3) (3x + 1) = 0
⇒ 2x + 3 = 0 or 3x + 1 = 0
i.e., x = -3 / 2 or x = -1/ 3
Question. Does there exist a quadratic equation whose coefficients are rational but both of its roots are irrational ?
Solution. Yes, there exists a quadratic equation whose coefficients are rational but both of its roots are irrational .
Consider the quadratic equation
x2 – 6x + 7 = 0
Here, D = b2 – 4ac
= (–6)2 – 4(1)(7)
⇒ D = 36 – 28 = 8
Since, discriminant is not a perfect square, therefore it will have irrational roots.
The roots will be
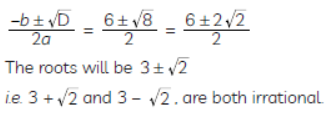
Question. Find the roots of the quadratic equation √2x2 + 7x + 5 √2 = 0 .
Solution. Given, quadratic equation is
√2x2 + 7x + 5 √2 = 0
On comparing the above equation with
ax2 + bx + x = 0
we get a = √2 , b = 7, c = 5 √2
Then, discriminant,
D = b2 – 4ac
= (7)2 – 4 × √2 × 5 √2
= 49 – 40 = 9
Now, x = −b ± √D/ 2a
= −7 ± √9 / 2 √2 = −7 ± 3 / 2 √2
∴ x = -4/ 2 √3 and -10/ 2√3
= -2 √3 and – 5 √3
Hence, the roots of the given equation is -2/ √3 and -5/ √3
Question. If b = 0 and c < 0, is it true that the roots of x2 + bx + c = 0 are numerically equal and opposite in sign ?
Solution. It is given that b = 0 and c < 0.
The given quadratic equation is:
x2 + bx + c = 0
On putting b = 0 in this equation, we get
x2 + 0.x + c = 0
x2 + c = 0
⇒ x2 = –c
Here, c < 0 ⇒ –c > 0
⇒ x = ± –c
Hence, the roots of x2 + bx + c = 0 are numerically equal and opposite in sign.
Question. Find the value of k for which the equation x2 + k(2x + k – 1) + 2 = 0 has real and equal roots.
Solution. Given, quadratic equation is:
x2 + 2xk + (k2 – k + 2) = 0
On comparing the quadratic equation, with ax2
+ bx + c = 0, we get:
a = 1, b = 2k, c = k2 – k + 2
Since, the roots of the above equation are real and equal.
∴ Discriminant, D = 0
i.e., b2 – 4ac = 0
(2k)2 – 4 × 1 × (k2 – k + 2) = 0
⇒ 4k2 – 4k2 + 4k – 8 = 0
⇒ 4k – 8 = 0
⇒ k = 2
Hence, the value of k is 2.
Question. If x = 2/ 3 and x = – 3 are roots of the quadratic equation ax2 + 7x + b = 0, find the values of a and b.
Solution. Since x = 2/ 3 and x = – 3 are the roots of the
quadratic equation
ax2 + 7x + b = 0
Now, sum of roots:
2 /3 + (- 3 ) = – 7/ a
⇒ – 7 /3 = – 7/ a ⇒ a = 3.
Product of roots:
⇒ 2/3 × (- 3 ) = b/ a
⇒ – 2 = b /3 [… a = 3]
⇒ b = – 6
Hence, the values of a and b are 3 and –6 respectively.
Question. If a and b are the roots of the equation x2 + ax – b = 0, then find a and b.
Solution. x2 + ax – b = 0
Sum of the roots = a + b
= Coefficient of x /Coefficient of x2 = -a
Product of roots = ab
= constant term / Coefficient of x2 = b
So, a + b = –a
⇒ b = –2a
and, ab = –b
⇒ a = –1
Putting the value of a, we get
b = –2 × (–1) = 2
Hence, a = –1 and b = 2.
Question. Solve for x :
x + 3 / x + 2 = 3x – 7/2x -3 , X 2 , 3/2
Solution. ⇒ (x + 3) (2x – 3) = (x + 2) (3x – 7)
⇒ 2x2 + 6x – 3x – 9 = 3x2 + 6x – 7x – 14
⇒ 2x2 – 3x2 + 3x + x – 9 + 14 = 0
⇒ – x2 + 4x + 5 = 0
⇒ x2 – 4x – 5 = 0
⇒ x2 – 5x + x – 5 = 0
(on splitting the middle term)
⇒ x (x – 5) + 1(x – 5) = 0
⇒ (x + 1) (x – 5) = 0
⇒ x = – 1, 5
Hence, the values of x are – 1 and 5.
Question. Solve for x: 2x + 9 + x = 13
Solution.

Question. Solve the following quadratic equation for x:
4x2 + 4bx – (a2 – b2) = 0
Solution. 4x2 + 4bx + b2 – a2 = 0
⇒ (2x + b)2 – (a)2 = 0
⇒ (2x + b + a)(2x + b – a) = 0
⇒ x = –a + b /2 + , x = a – b / 2
Question. Find the value of p, for which one root of the quadratic equation px2 – 14x + 8 = 0 is 6 times the other.
Solution.

Question. Determine the condition for one root of the quadratic equation ax2 + bx + c = 0 to be thrice the other.
Solution. Let the roots of the equation ax2 + bx + c be α and 3α.
Then, sum of the roots = α + 3α
= 4α = − b /a
α= − b/ 4a
Product of the roots = α × 3α
= 3α2 = c/a
3 (−ba/4a) = c/a
3b2/ 16a2 = c/a
Question. The sum of the areas of two squares is 157 m2. If the sum of their perimeters is 68 m, find the sides of the two squares.
Solution. Let ‘x’ and ‘y’ be the length of the sides of the two squares.the, area of first square = (side)2 = x2
area of second square = (side)2 = y2
According to the question,
x2 + y2 = 157
Now, the perimeter of the first square = 4 × side = 4x
Perimeter of the second square = 4 × side = 4y
According to the question:
4x + 4y = 68
or x + y = 17
y = 17 – x …(ii)
Put the value of ‘y’ from equation (ii), in equation (i).
⇒ x2 + (17 – x)2 = 157
⇒ x2 + 289 + x2 – 34x – 157 = 0
⇒ 2x2 – 34x + 132 = 0
⇒ x2 – 17x + 66 = 0
⇒ (x – 6) (x – 11) = 0
∴ x = 6 or 11
When, x = 6, then y = 11
when, x = 11, then y = 6
Hence, the sides of the squares are 6 m and 11m.
Question. Write all the values of p for which the quadratic equation x2 + px + 16 = 0 has equal roots. Find the roots of the equation so obtained.
Solution. Given equation: x2 + px + 16 = 0
Here, a = 1, b = p, c = 16
Discriminant, D = b2 – 4ac
= p2 – 4 × 1 × 16
= p2 – 64
If roots are equal, then:
D = 0
i.e. p2 – 64 = 0
⇒ p2 = 64
⇒ p = ± 8
∴ Equation is x2 ± 8x + 16 = 0
⇒ (x ± 4)2 = 0 [∵ (a + b)2 = a2 ± 2ab + b2]
⇒ x ± 4 = 0
⇒ x = – 4, 4
Hence, roots are x = – 4 and x = 4 and the values of p are – 8 and 8.
Question. The product of two successive integral multiples of 5 is 1050. Determine the multiples.
Solution. Let two successive integral multiples of 5 be x and (x + 5)
According to question,
x(x + 5) = 1050
x2 + 5x – 1050 = 0
(x – 30) (x + 35) = 0
x = 30 or –35
When x = 30,
Multiples are 30 and 30 + 5 = 35
When x = –35,
Multiples are –35 and –35 + 5 = –30
Question. If the equation (1 + m2)x2 + 2 mcx + c2 – a2 = 0 has equal roots then show that c2 = a2(1 + m2).
Solution. Given: A quadratic equation is :
(1 + m2)x2 + 2 mcx + c2 – a2 = 0
To prove: (1 + m2) x2 + 2mcx + c2 – a2 = 0, with
equal roots c2 = a2 (1 + m2)
we get
A = 1 + m2, B = 2 mc, C = c2 – a2
The roots of the given equation is equal, then
Discriminant, D = 0
∴ B2 – 4AC = 0
(2 mc)2 – 4 × (1 + m2) (c2 – a2) = 0
⇒ 4m2c2 – 4(c2 + c2m2 – a2 – a2m2) = 0
⇒ 4m2c2 – 4c2 – 4c2m2 + 4a2 + 4m2a2 = 0
⇒ m2a2 + a2 – c2 = 0
⇒ c2 = m2a2 + a2
⇒ c2 = a2 (1 + m2) Hence, proved
Question. If the roots of the equation (a2 + b2)x2 – 2(ac + bd)x + (c2 + d2) = 0 are equal, prove that b/ a = d /c
Solution.

Question. Find the dimensions of a rectangular park whose perimeter is 60 m and area 200 m2.
Solution. Let ‘l‘ be the length and ‘b’ be the breadth of the rectangular park.
Perimeter of the park, p = 2(l + b)
Area of the park, A = l × b
According to the given conditions:
2(l + b) = 60
⇒ l + b = 30
⇒ l = 30 – b ….(i)
and lb = 200
(30 – b)b = 200 from (i)]
⇒ 30b – b2 = 200
b2 – 30b – 200 = 0
on splitting the middle term, we get:
⇒ b2 – 20b – 10b + 200 = 0
⇒ (b – 20) (b – 10) = 0
⇒ b = 20 or 10
when b = 20m, l = 10 m
when b = 10m, l = 20 m
Hence, the length and breadth of the rectangle are 10 m and 20 m or 20 m and 10 m respectively.
Question. A train travels 360 km at a uniform speed. In the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution. Let, the actual speed of the train be ‘x’ km/hr.
Time taken by the train at actual speed,
t1 = 360 /x hr
Increased speed of the train = (x + 5) km / hr
Time taken by the train at the increased speed t2 = 360/ x + 5. hr
According to the given condition:
t1 – t2 = 1
⇒ 360/x – 360/ x + 5 = 1
⇒ 360 (x + 5- 5 x)/ (x + 5) x = 1
⇒ 360 × 5 = x2 + 5x
⇒ x2 + 5x – 1800 = 0
⇒ x2 + 5x – 1800 = 0
⇒ x2 + 45x – 40x – 1800 = 0
⇒ x(x + 45) – 40(x + 45) = 0
⇒ (x – 40) (x + 45) = 0
⇒ x = 40 [∵ x = – 45, is
not possible as speed cannot be negative]
Hence, the actual speed of the train is 40 km/hr.
Question. Solve for x : 1/ a + b + x = 1/a + 1/b + 1/x ;
a ≠ b ≠ 0, x ≠ 0, x ≠ – (a + b)
Solution. 1/ a + b + x = 1/a + 1/b + 1/x

⇒ – ab = ax + bx + x2
⇒ x2 + ax + bx + ab = 0
⇒ x(x + a) + b(x + a) = 0
⇒ (x + b) (x + a) = 0
⇒ x = – a, – b
Hence, the values of x are – a and – b.
Question. Find a natural number whose square diminished by 84 is equal to thrice of 8 more than the given number.
Solution. Let n be the required natural number.
According to the question:
Square of natural number diminished by
84 gives n2 – 84.
Thrice of 8 more than given number = 3(8 + n).
According to the question,
n2 – 84 = 3(8 + n)
⇒ n2 – 84 = 24 + 3n
⇒ n2 – 3n – 108 = 0
Splitting the middle term, we have
⇒ n2 – 12n + 9n – 108 = 0
⇒ n(n –12) + 9(n – 12) = 0
⇒ (n – 12)(n + 9) = 0
n = 12 or n = –9
But n ≠- 9 as n is a natural number.
Hence, the required natural number is 12.
Question. If the roots of the quadratic equation (a – b)x2 + (b – c)x + (c – a) = 0 are equal, prove that b + c = 2a. Solution.


Question. A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
Solution. Let n be the required natural number.
According to the question, number when
increased by 12 is n + 12.
160 times number’s reciprocal = 160 (1/n ) = 160/n
⇒ n(n + 12) = 160
⇒ n2 + 12n – 160 = 0
Splitting the middle term, we have
n2 + 20n – 8n – 160 = 0
n(n + 20) – 8(n + 20) = 0
(n + 20)(n – 8) = 0
n = –20 or 8
But n ≠ -20 as n is a natural number.
Hence, the required number is 8.
Question. At t minutes past 2 pm, the time needed by the minutes hand of a clock to show 3 pm was found to be 3 minutes less than t2/4 minutes. Find t.
Solution. It is given that at t minutes past 2 pm, the time needed by the minute hand to show 3 pm was found to be 3 minutes less than t2/4 min.
⇒ t + (t2/ 4 – 3) = 60
[ ∴ time between 2 pm and 3 pm
= 1 hour = 60 min.]
⇒ 4t + t2 – 12 = 240
⇒ t2 + 4t – 12 – 240 = 0
⇒ t2 + 4t – 252 = 0
Splitting the middle term, we have
t2 + 18t – 14t – 252 = 0
⇒ t(t + 18) –14(t + 18) = 0
⇒ (t + 18)(t – 14) = 0
t = –18 or t = 14.
But t ≠ -18 as time cannot be negative
⇒ t = 14
Hence, the required value of t is 14 minutes.
Question. A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
Solution. Let ‘x’ km / hr be the speed of the plane.
Increased speed = (x + 250) km / hr 67
⇒ x2 + 250 x = 250 × 3000
⇒ x2 + 250 x – 750000 = 0
⇒ x2 + 1000 x – 750 x – 750000 = 0
⇒ x (x + 1000) – 750 (x + 1000) = 0
⇒ (x – 750) (x + 1000) = 0
⇒ x = 750 or – 1000
⇒ x = 750 [∵ speed cannot be negative]
Hence, the usual speed of the plane is 750 km/hr.
Question. If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than five times her actual age. What is her age now?
Solution. Let actual age of Zeba be x years.
Her age when she was 5 years younger
= (x – 5) years.
According to the condition given in question:
Square of her age = 11 more than 5 times her actual age
(x – 5)2 = 11 + 5(x)
⇒ x2 + 25 – 10x = 11 + 5x
[ a (a – b)2 = a2 + b2 – 2ab]
⇒ x2 – 10x – 5x + 25 – 11 = 0
⇒ x – 15x + 14 = 0
Splitting the middle term, we have
⇒ x2 – 14x – x + 14 = 0
⇒ x(x – 14) –1(x – 14) = 0
⇒ (x – 14)(x – 1) = 0
⇒ x = 14 or x = 1
But x ≠ +1 as in that case (x – 5) will not be possible
⇒ x = 14
Hence, Zeba’s age now is 14 years.
Question. At present, Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha.
Solution. Let Nisha’s present age be x years.
Then, Asha’s present age = (2 + x2) [By the given conditon]
Now, when Nisha grows to her mother’s
present age i.e. after {(x2 + 2) – x} years.
Then, Asha’s age will become {(x2 + 2) – x} years.
Now by the given condition,
Asha’s age = 1 year less than 10 times present age of Nisha.
(2 + x2) + {(x2 + 2) – x} = 10x – 1
⇒ 2 + x2 + x2 + 2 – x = 10x – 1
⇒ 2x2 – 11x + 5 = 0
Splitting the middle term, we have
⇒ 2x2 – 10x – x + 5 = 0
⇒ 2x(x – 5) – 1(x – 5) = 0
⇒ (x – 5)(2x – 1) = 0
⇒ (x – 5)(2x – 1) = 0
⇒ x = 5 or x = 1/2
But x ≠ 1/2 as then Nisha’s age = 1/2 . This means that her mother Asha’s age = (x2 + 2) = (1/4 + 2) = 2, 1/4 years which is not possible.
Hence, the present age of Nisha = 5 years and the present age of Asha = x2 + 2 = 52 + 2 = 25 + 2 = 27 years
Question. In a class test, the sum of Arun’s marks in Hindi and English is 30. Had he got 2 marks more in Hindi and 3 marks less in English, the product of the marks would have been 210. Find his marks in the two subjects.
Solution. Let, the Arun’s marks in Hindi be x.
Then, marks in English = 30 – x
According to the given condition,
⇒ (x + 2) (30 – x – 3) = 210
⇒ (x + 2) (27 – x) = 210
⇒ 27x + 54 – x2 – 2x = 210
⇒ x2 – 25x + 156 = 0
x2 − 13x −12x + 156 = 0
x (x − 13) − 12(x − 13) = 0
⇒ (x – 13) (x – 12) = 0
⇒ x = 13 or 12
When : x = 13
Marks in Hindi = 13
Marks in English = 30 – 13 = 17
When : x = 12
Marks in Hindi = 12
Marks in English = 30 – 12 = 18
Hence, the marks obtained in the two subjects are (13, 17) or (12, 18).
Question. Solve for x : x + 3 /x – 2 -1 – x = 17/ 4 ; 0, 2
Solution. x + 3 /x – 2 – (1 – x) = 17/ 4 75
⇒ (x2 + 3x – 3x + 2 + x2) × 4 = 17(x2 – 2x)
⇒ 4(2x2 + 2) = 17x2 – 34x
⇒ 8x2 + 8 = 17×2 – 34x
⇒ 17x2 – 8x2 – 34x – 8 = 0
⇒ 9x2 – 34x – 8 = 0
⇒ 9x2 – 36x + 2x – 8 = 0
⇒ 9x(x – 4) + 2(x – 4) = 0
⇒ (9x + 2) (x – 4) = 0
⇒ x = – 2/9 , 4
Hence, the values of x are – 2 /9 , 4
Question. A motor boat whose speed is 18 km/hr in still water takes 1 hr more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution. Let, the speed of the stream be x km/hr.
Speed of the boat in still water = 18 km/hr
∴ The speed of the boat in upstream
= (18 – x) km/hr
The speed of the boat in downstream
= (18 + x) km/hr.
Total distance to be covered = 24 km
∴ Time taken in upstream, t1 = 24 /(18 − x) hr
Time taken in downstream, t2 = 24 (18 + x) hr
According to the question,
24 /18 – x – 24/18 + x = 1
⇒ 24 (18 + x – 18 + x) / (18 – x) (18 + x ) = 1
⇒ 24 × 2x = 324 – x2
⇒ x2 + 48x – 324 = 0
⇒ x2 + 54x – 6x – 324 = 0
⇒ x(x + 54) – 6 (x + 54) = 0
⇒ (x + 54) (x – 6) = 0
x ≠ – 54 (∵ speed can’t be negative)
∴ x = 6
Hence, the speed of the stream is 6 km/hr.
Question. A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr more than its original speed. If it takes 3 hours to complete total journey, what is the original average speed ?
Solution. Let the original speed of the train be ‘x’ km/hr.
Increased speed = (x + 6) km/hr
Now, time taken to cover 60 km at original
speed, t1 = 63/ x. hr
Time taken to cover 72 km at increased speed:
t2 = 72 /x + 6. hr
63/x + 72/ x + 6 = 3
⇒ 63 x + 378 + 72x / x (x + 6) = 3
⇒ 135 x + 378 = 3 (x2 + 6x)
⇒ 3x2 + 18x – 135x – 378 = 0
⇒ 3x2 – 117x – 378 = 0
⇒ x2 – 42x + 3x – 126 = 0
⇒ x(x − 42) + 3(x − 42) = 0
⇒ (x – 42) (x + 3) = 0
x = – 3
(∵ speed can’t be negative)
∴ x = 42
Hence, the original average speed of train is 42 km/hr.
Question. The altitude of a right-angled triangle is 7 cm less than its base. If the hypotenuse is 13 cm, then find the other two sides.
Solution. Let, the base of the right angled triangle be ‘x’ m.
Then, the altitude of a right-angled triangle is (x – 7) cm.
And, the hypotenuse of right angled triangle = 13 cm
Then, by the pythagoras theorem
H2 = P2 + B2
⇒ 132 = (x – 7)2 + x2
⇒ 169 = x2 + 49 – 14x + x2
⇒ 2x2 – 14x – 120 = 0
⇒ x2 – 7x – 60 = 0
⇒ x2 – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5(x – 12) = 0
⇒ (x + 5) (x – 12) = 0
⇒ x = 12
(∵ x = – 5 is not possible)
The base of the right angled triangle = 12 cm
and altitude = 12 – 7 = 5 cm.
Hence, the other two sides of triangle are 5 cm and 12 cm.
Question. Find two consecutive odd natural numbers, the sum of whose squares is 394.
Solution. Let, the first number be x
and the second number be (x + 2).
According to the given condition,
x2 + (x + 2)2 = 394
⇒ x2 + x2 + 4 + 4x = 394
⇒ 2x2 + 4x – 390 = 0
⇒ x2 + 2x – 195 = 0
⇒ x2 + 15x – 13x –195 = 0
⇒ x(x + 15) – 13 (x + 15) = 0
⇒ (x – 13) (x + 15) = 0
⇒ x = 13, – 15
x ≠ –15
[∵ natural numbers are negative]
Hence, the two consecutive odd natural numbers are 13 and 15.
Question. A and B working together can do a work in 6 days. If a takes 5 days less than B to finish the work, in how many days can B can do the work alone?
Solution. Let B take ‘x’ days to complete the work.
Then, A takes (x – 5) days to complete the work done.
According to the given condition:
1/ x + 1/ x – 5= 1 / 6
⇒ x – 5 + x /x (x- 5) = 1/ 6
⇒ 6(2x – 5) = x2 – 5x
⇒ x2 – 5x – 12x + 30 = 0
⇒ x2 – 17x + 30 = 0
⇒ x2 – 15x – 2x + 30 = 0
(on splitting the middle term)
⇒ x(x – 15) – 2(x – 15) = 0
⇒ (x − 15)(x − 2) = 0
⇒ x = 2 or 15
But x = 2 is not possible as x < 5.
∴ x = 15
Hence, B takes 15 days to complete the work alone.
Question. Find x in terms of a, b and c :
a/ x – a + b/ x – b = 2 c / x – c , x ‘ a ,b , c
Solution.

Question. Solve for x : 81
2x / x – 3 + 1 /2x + 3 + 3x + 9 / (x -3) (2x + 3) = 0 ,
x ≠ 3, – 3/2
Solution.


Question. Solve for x:
x – 1/ 2x + 1 + 2x +1 / x -1 = 2, where x ≠-1/2 , 1.
Solution.

Question. Using quadratic formula, solve the following equation for x : 4
abx2 + (b2 – ac)x – bc = 0
Solution. We have, abx2 + (b2 – ac) x – bc = 0
Comparing this equation with Ax2 + Bx + C = 0, we get
A = ab, B – b2 – ac, C = -bc
∴ D = B2 – 4AC
= (b2 – ac)2 – 4(ab)(-bc)
= b4 + a2c2 – 2ab2c + 4ab2c
= b4 + 2ab2c + a2c2
= (b2 )2 + 2(b2 )(ac) + (ac)2
= (b2 + ac)2 > 0
So, the roots of the given equation are real and are given by :
Question. Find the roots of the quadratic equation 2x2 – 7x – 3 = 0 by the method of completing the square.
Solution. We have, 2x2 – 7x – 3 = 0

Question. The sum of the ages of a woman and her daughter is 40 years. The product of their ages five years ago was 125 years. Find their present ages.
Solution. Let the present age of the woman be x years. Then, the present age of her daughter is (40 – x) years.
Five years ago, Age of woman = (x – 5) years
and, Age of daughter = (40 – x – 5) years = (35 – x) years.
According to the given question, (x – 5) (35 – x) = 125
⇒ 35 x – x2 – 175 + 5x – 125 = 0
⇒ x2 – 40 x + 300 = 0
⇒ (x – 30) (x – 10) = 0
⇒ x – 30 = 0 or x – 10 = 0
⇒ x = 30 or x = 10
when, x = 30, then 40 – x = 40 – 30 = 10
Thus, when the woman’s present age is 30 years, her daughter’s present age is 10 years.
When, x = 10, then 40 – x = 40 – 10 = 30, which is absurd, because the woman’s age cannot be less than her daughter’s age.
Hence, present age of woman = 30 years and, present age of daughter = 10 years.
Question. Find the value(s) of k for which the following equation has equal roots.
(k – 12)x2 +2(k – 12)x+2= 0
Solution. We have, (k -12)x2 + 2(k -12)x + 2 = 0
Here, a = k – 12, b = 2 (k – 12), c = 2
∴ D = b2 – 4ac = 4(k – 12)2 – 4 (k – 12) × 2
= 4 (k -12) [(k -12) – 2]
= 4(k -12)(k -14)
The given equation will have equal roots if D = 0.
⇒ 4 (k -12) (k -14) = 0
⇒ k – 12 = 0 or k – 14 = 0
⇒ k = 12 or k = 14 Ans.
Question. By increasing the list price of a book by Rs. 10 a person can buy 10 less books for Rs. 1,200. Find the original list price of the book.
Solution. Let the original list price of book = Rs. x.
and, the increased list price of a book = Rs. (x + 10)

Question. Determine if x = 3 is a root of the given equation or not :

Solution. At x = 3

Question. A plane left 30 minutes later than the schedule time and in order to reach its destination 1500 km away in time it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.
Solution. Let the usual speed of the plane be x km/hr. Then
Time taken to cover 1500 km with the usual speed = 1500 / x hrs.
Time taken to cover 1500 km with the speed of (x + 250) km/hr = 1500 / x + 2500 hrs.
According to given question, 1500/x – 1500/ x + 250 = 30/60
⇒ 1500x + 1500 x 250 – 1500x / x(x + 250) = 1/2
⇒ 1500 x 250 / x2 + 250x = 1/2
⇒ x2 + 250x – 750000 = 0
⇒ x2 + 1000x – 750 x – 750000 = 0
⇒ x (x + 1000) – 750 (x + 1000) = 0
⇒ (x – 750) (x + 1000) = 0
⇒ x = 750 or x = – 1000
⇒ x = 750 [∴ speed cannot be negative]
Hence, the usual speed of the plane is 750 km/hr.
Question. A two digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.
Solution. Let the tens digit be x.
Then, the units digit = 18/x

Question. The hypotenuse of a right triangle is 3 √5 cm. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be 15 cm. Find the length of each side.
Solution. Let the smaller side of the right triangle be x cm and the larger side be y cm. Then,

Question. Find the roots of the quadratic equation 8x2 – 22x – 21 = 0 by factorization.
Solution. We have, 8x2 – 22x – 21 = 0
⇒ 8x2 – 28x + 6x – 21 = 0
⇒ 4x (2x – 7) + 3 (2x – 7) = 0
⇒ (4x + 3) (2x – 7) = 0
⇒ 4x + 3 = 0 or 2x – 7 = 0

Assignments for Class 10 Mathematics Quadratic Equation as per CBSE NCERT pattern
All students studying in Grade 10 Mathematics Quadratic Equation should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Quadratic Equation exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Quadratic Equation which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.
Some advantages of Free Assignments for Class 10 Mathematics Quadratic Equation
- Solving Assignments for Mathematics Quadratic Equation Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
- By solving one assignments given in your class by Mathematics Quadratic Equation teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
- You will be able to understand the type of questions which are expected in your Mathematics Quadratic Equation class test
- You will be able to revise all topics given in the ebook for Class 10 Mathematics Quadratic Equation as all questions have been provided in the question banks
- NCERT Class 10 Mathematics Quadratic Equation Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
- Parents will be able to take print out of the assignments and give to their child easily.
All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Quadratic Equation teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Quadratic Equation Assignments PDF.

You can download free assignments for class 10 Mathematics Quadratic Equation from https://www.assignmentsbag.com
You can get free PDF downloadable assignments for Grade 10 Mathematics Quadratic Equation from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided assignments for all subjects in Grade 10, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge
Yes all test papers for Mathematics Quadratic Equation Class 10 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.
https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.

