Assignments For Class 10 Mathematics Real Numbers

Assignments for Class 10 Mathematics Real Numbers have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Real Numbers from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Real Numbers. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Real Numbers book and get good marks in class 10 exams.

Class 10 Mathematics Real Numbers Assignments

Question. Let a, b and c be real numbers, such that a -7b+8c = 4and 8a + 4b -c = 7, then the value of     
a² – b² + c²…..
(A) -1
(B) 4
(C) -2
(D) 1

Question. The H.C.F & L.C.M of two numbers are 13 and 455 respectively. If one of the numbers lies b/w 75 and 125, find the numbers.     
(A) 91
(B) 95
(C) 97
(D) None of these

Question. If the L.C.M of the polynomials (y – 3)^a (2y + 1)^b (y + 13)⁷ and (y – 3)⁴(2y + 1)⁹ (y + 13)^c is (y –3)⁶ (2y + 1)¹⁰ (y+ 13)⁷, then the least value of a + b + c is.   
(A) 16
(B) 18
(C) 20
(D) None of these

Question. If a < b < c < d < e are consecutive positive integers, such that b + c+ d is a perfect square and a +b + c + d + e is a perfect cube. What is the smallest possible value of c?       
(A) 675
(B) 576
(C) 475
(D) 384

Question. If we divide a two digit number by the sum of its digits we get 4 as quotient and 3 as remainder.
Now if we divide that two digit number by the product of its digits, we get 3 as quotient and 5 as remainder. The two digit number is:         
(A) Even
(B) Odd prime
(C) Odd composite
(D) Odd

Question. Four positive integers sum to 125. If the first of these numbers is increased by 4, the second is decreased by 4, the third is multiplied by 4 and the fourth is divided by 4, we find four equal numbers, then four original integers are:     
(A) 16, 24, 5, 80
(B) 8, 22, 38, 57
(C) 7, 19, 46, 53
(D) 12, 28, 40, 45

Question. Find the smallest number that leaves a remainder of 4 on division by 5, 5 on division by 6, 6 on division by 7, 7 on division by 8 and 8 on division by 9?   
(A) 9125
(B) 20779
(C) 9711
(D) 2519

Question. There are two numbers such that a>b, H.C.f (a, b) = h and Lcm (a, b) = l, what is the L.C.M of a – b and b. 
(A) (a – b)b /h
(B) a – b
(C) b /h
(D) None of these

Question. What is the least number which when divided by 42, 72 and 84 leaves the remainder 25, 55 and 67 respectively?     
(A) 521
(B) 512
(C) 504
(D) 487

Question. y, z are integers, then the value of x + y + z is:   
(A) 6
(B) 8
(C) 7
(D) -2

Question. A positive integer n has 60 divisors and 7 n has 80 divisors. What is the greatest integer k such that 7k divides n?
(A) 0
(B) 1
(C) 2
(D) 3

Question. The least multiple of 7 which leaves a remainder of 4 when divided by 6, 9, 12 and 18 is.   
(A) 362
(B) 365
(C) 364
(D) None of these

Question. The greatest number which can divide 1356, 1868, 2764 leaving same remainder 12 in each case is?   
(A) 63
(B) 64
(C) 65
(D) None of these

Question. What is the largest integer that is a divisor of (n +1) (n+3) (n+5) (n+7) (n+9) for all positive even integers n?
(A) 3
(B) 5
(C) 11
(D) 15

Question. The sum of seven consecutive natural numbers is 1617. How many of these are prime?
(A) 4
(B) 5
(C) 2
(D) 7

CBSE Class 10 Mathematics Real Numbers Assignment Set A

CBSE Class 10 Mathematics Real Numbers Assignment Set B

CBSE Class 10 Mathematics Real Numbers Assignment Set C

CBSE Class 10 Mathematics Real Numbers Assignment Set D

CBSE Class 10 Mathematics Real Numbers Assignment Set E

CBSE Class 10 Mathematics Real Numbers Assignment Set F

CBSE Class 10 Mathematics Real Numbers Assignment Set G

CBSE Class 10 Mathematics Real Numbers Assignment Set H

CBSE Class 10 Mathematics Real Numbers Assignment Set I

CBSE Class 10 Mathematics Real Numbers Assignment Set J

CBSE Class 10 Mathematics Real Numbers Assignments Set A

CBSE Class 10 Mathematics Real Numbers Assignments Set B

CBSE Class 10 Mathematics Real Numbers Assignments Set C

CBSE Class 10 Mathematics Real Numbers Assignments Set D

CBSE Class 10 Mathematics Real Numbers Assignments Set E

CBSE Class 10 Mathematics Real Numbers Assignments Set F

CBSE Class 10 Mathematics Real Numbers Assignments Set G

CBSE Class 10 Mathematics Real Numbers Assignments Set H

CBSE Class 10 Mathematics Real Numbers Assignments Set I

Integers : Set of Whole Numbers (0,1,2,…) with their assistive inverse.{-3,-2,-1,0,1,2,3…}

Irrational Numbers : Number that cannot be written as ratio 0.25,0.3,4.2 etc. Rational numbers can be expressed as terminating or non- terminating decimal numbers.

Related Theorem and Identities
For any two positive integers a and b, HCF (a,b) × LCM (a,b) = a×b

Fundamental Theorem of Arithmetic – “Composite number =Product of prime numbers”

Euclid’s Division Lemma state that “Given positive integers a and b, there exist unique integers q and r satisfying a= bq+r,0 ≤ r< b”

Euclid’s Division Algorithm : To obtain the HCF of two positive integers, say c and d with c >d, we follow the steps below:

Step 1. Apply Euclid’s division lemma to find q and r where c = dq+r,0 ≤ r< d”

Step 2. If r=0 is the HCF of . If  r≠0 then apply Euclid’s division lemma to d and r.

Step 3. Continue this process till the remainder is zero. the divisor at this stage will be the required HCF.

Solved Problems on Class 10 Real Numbers

Question. A rational number in its decimal expansion is 1.7112. What can you say about the prime factors of q, when this number is expressed in the form p/q?
sol.  q has the factors of the form 2n ´5m for whole numbers n and m

Question.  Using prime factorisation method, find the LCM of 21, 28, 36, 45.
sol. 1260

Question.  The length, breadth and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm respectively.
Determine the longest rod which can measure the three dimensions of the room exactly.
sol. 75cm

Question. What can you say about the prime factorisation of the denominators of the rational number 0.134?
sol. Since 0.134 has non-terminating repeating decimal expansion, its denominator has factors other than 2 or 5.

Question. On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 45 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
sol. 2520 cm

Question. The numbers 525 and 3000 are both divisible only by 3, 5, 15, 25 and 75. What is HCF (525, 3000)? Justify your answer.
sol.  HCF = 75, as HCF is the highest common factor.

Question. Find the greatest number that will divide 445, 572 and 699 leaving remainders 4, 5 and 6 respectively.
sol. 63

Question. Write the denominator of the rational number 257/5000 in the form 2 5 m × n, where m, n are non-negative integers. Hence, write its decimal expansion, without actual division.
sol. 2³×5⁴, 0.0514

Question. A positive integer is of the form 3q +1, q being a natural number. Can you write its square in any form other than 3m+1 i.e., 3m or 3m+2 for some integer m? Justify your answer.
sol.  No. (3q +1)² = 9q² +6q +1 = 3 (3q² +2q) + 1 = 3m+1.

Question. If the HCF (210, 55) is expressible in the form 210 × 5 – 55y, find y .
sol. y=19

Question. Write whether every positive integer can be of the form 4q +2, where q is an integer. Justify your answer.
Sol.  No, because an integer can be written in the form 4q, 4q +1 , 4q +2, 4q +3.

Question. Can the numbers 6n, n being a natural number end with the digit 5? Give reasons.
sol.  No, because 6n = (2´3)n = 2n ´3n, so the only primes in the factorisation of 6n are 2 and 3, and not 5.

Question. Use Euclid’s division algorithm to find the HCF of 4052 and 12576.
sol. 4

Question. The product of the LCM and HCF of two natural numbers is 24. The difference of two numbers is 2. Find the numbers. 
Solution. Let the natural numbers be p and q. According to question,
p × q = 24 …(i)
and p – q = 2
p = 2 + q …(ii)
From (i) and (ii)
(q + 2) × q = 24
q² + 2q –24 = 0
q² + 6q – 4q – 24 = 0
(q + 6) (q – 4) = 0
q = – 6, 4
q = 4
[Since –6 is not a natural number] So, the numbers are 4, 6.

Question. Show that the square of any positive odd integer is of the form 8m + 1, for some integer m.
Solution. Let a be any positive integer.
So, it is of the form 2q + 1, for some integer q i.e. a = 2q + 1
⇒ a² = (2q + 1)² = 4q² + 4q + 1
= 4q (q + 1) + 1
Now, q (q + 1) is either 0 or even. So, it is 2m,
where m is a whole number
⇒ a² = (2q + 1)²
= 4 × 2m + 1 i.e. 8m + 1

Question. Prove that √p + √q is irrational, where p and q are primes.
Solution. Let us suppose that √p + √q is rational.
Let √p + √q = a, where a is a rational number,
⇒ √p = a – q
On squaring both sides, we get
⇒ p = a² + q − 2a √q
[Using (a − b)² = a² + b² − 2ab]
⇒ √q = a² + q – /2a 
Therefore, the above statement is a contradiction as the right hand side is a rational number, while the left hand side √q is irrational, since p and q are prime numbers.
So, our assumption is wrong. Hence, √p + √q is irrational.

Question. Two alarm clocks ring their alarms at regular intervals of 72 seconds and 50 seconds if they first beep together at 12 noon, at what time will they beep again for the first time?
Solution. Here, we need to find the LCM of 72 and 50.
72 = 2 × 2 × 2 × 3 × 3
50 = 2 × 5 × 5
LCM of 72 and 50 = 2³ × 3² × 5² = 1800 So, 1800 sec = 30 min
Hence, alarm clocks will beep again for the first time at 12.30 pm.

Question. Find the HCF of 612 and 1314 using prime factorisation. 
Solution. Prime factors of 612 and 1314.
612 = 2 × 2 × 3 × 3 × 17
1314 = 2 × 3 × 3 × 73
HCF (612, 1314) = 2 × 3 × 3 = 18
Hence, the HCF of 612 and 1314 is 18.

Question. On a morning walk, three people step off together and their steps measure 40 cm, 42 cm and 45 cm respectively. What is the minimum distance each should walk, so that each can covers the same distance in complete steps?
Solution. We know that the LCM is the product of the greatest power of each prime factor of the numbers.
We have to find the LCM of 40, 42 and 45 to get the required minimum distance.
For this, we find prime factorisation,
40 = 2 × 2 × 2 × 5
42 = 2 × 3 × 7
45 = 3 × 3 × 5
LCM (40, 42, 45) = 2 × 3 × 5 × 2 × 2 × 3 × 7 = 2520
Hence, each person should walk a minimum distance of 2520 cm, so that each of them can cover the same distance in complete steps.

Question. Write the smallest number which is divisible by both 306 and 657. 
Solution. Given numbers are 306 and 657.
The smallest number divisible by 306 and 657 = LCM(306, 657)
prime factors of 306 = 2 × 3 × 3 × 17
prime factors of 657 = 3 × 3 × 73
The LCM of (306, 657) = 2 × 3 × 3 × 17 × 73 = 22338
Hence, the smallest number divisible by 306 and 657 is 22,338.

Question. Check whether 12ⁿ can end with the digit 0 for any natural number n. 
Solution. Let, if possible, 12ⁿ have a value which ends with the digit 0. ⇒ 10 is a factor of 12ⁿ
⇒ 5 is a prime factor of 12ⁿ
i.e., 12ⁿ = 5 × q, where q is some natural number
⇒ (2² × 3)ⁿ = 5 × q
or 22ⁿ × 3ⁿ = 5 × q
The assumption, 5 is a prime factor of 22ⁿ × 3ⁿ, is not possible because 22ⁿ× 3ⁿ can have only 2 and 3 as prime factors.
Hence, our assumption is wrong and 12ⁿ cannot end with the digit 0.

Question. Using prime factorisation method, find the HCF and LCM of 210 and 175. 
Solution. The prime factorisations of 210 and 175 are:
210 = 2 × 3 × 5 × 7
175 = 5 × 5 × 7
So, HCF (210, 175) = 5 × 7 = 35; and
LCM (210, 175) = 2 × 3 × 5 × 7 × 5 = 1050

Question. Prove that the number 4ⁿ, n being a natural number, can never end with the digit 0.
Solution. If 4n ends with 0, then it must have 5 as a factor But, (4)ⁿ = (2²)ⁿ = 2²ⁿ, i.e., the only prime factor of 4ⁿ is 2.
Also, we know from the Fundamental Theorem of Arithmetic that the prime factorisation of each number is unique.
∴ 4ⁿ can never end with 0.

Question. Find the two numbers which on multiplication with √360 gives a rational number. Are these numbers rational or irrational? 
Solution. √360 = √2×2×2×3×3×5
=6 √10
If we multiply 6 10 with 10 and 1.
We get,
6 √10 × √10×1 = 60
Hence, numbers are 10 and 1.
Where, 1 is a rational number and 10 is an irrational number.

Question. Prove that √5 is an irrational number. 
Solution. Let us assume, to the contrary, that √5 is a rational number and its simplest form is a / b , where a and b are integers having no common factor other than 1 and b ≠ 0.
Now,  √5 = a/ b
⇒ 5 = a² / b²
⇒ 5b² = a² …(i)
⇒ a2 is divisible by 5 [∵ 5b2 is divisible by 5]
⇒ a is divisible by 5 [∵ 5 is a prime number
and divides a² ⇒ 5 divides a]
Let a = 5c, for some integer ‘c’
On substituting a = 5c in (i), we get 5b2 = (5c)²
⇒ 5b² = 25c²
⇒ b² = 5c²
⇒ b² is divisible by 5 [∵5c² is divisible by 5]
⇒ b is divisible by 5
Since a and b are both divisible by 5, 5 is common factor of a and b.
But this contradicts the fact that a and b have no common factor other than 1.
This contradiction has arisen because of our incorrect assumption that √5 is a rational number.
Hence, √5 is irrational.

Question. Using prime factorisation, find HCF and LCM of 18, 45 and 60. Check if HCF × LCM = product of the numbers.
Solution. Here, 18 = 2 × 3²
45 = 3² × 5 and 60 = 22 × 3 × 5
So, HCF (18, 45, 60) = 3; and
LCM (18, 45, 60) = 2² × 3² × 5 = 180
Clearly, HCF × LCM = 3 × 180 = 540
whereas, product of numbers
= 18 × 45 × 60 = 48600
Hence, HCF × LCM ≠ Product of numbers.

Question. Prove that √2 is an irrational number. 
Solution. Let us assume √2 be a rational number and its simplest form be a b , a and b as coprimes.
So, √2 = a/ b
⇒ a2 = 2b²
Thus, a² is a multiple of 2.
⇒ a is a multiple of 2. …
Let a = 2 m for some integer m.
Then, b² = 2 m²
Thus, b2 is a multiple of 2.
⇒ b is a multiple of 2. …
From (i) and (ii,) 2 is a common factor of a and b.
This contradicts the fact that a and b are coprimes.
Hence, √2 is an irrational number.

Question. Write the denominator of rational number 257/ 5000 in the form 2^m × 5ⁿ, where m, n are non-negative integers. Then, write its decimal expansion without actual division.
Solution. Denominator of the rational number 257/ 5000 is 5000.
Now, 5000 = 2 × 2 × 2 × 5 × 5 × 5 × 5
= (2)³ × (5)⁴
which is of the type 2m × 5n,
where m = 3 and n = 4 are non–negative integers.
Simplifying the given fraction:
⇒ 257/ 5000 = 257/ 5⁴ ×2³
= 257 ×  54 × 23 ×2/2
= 514/ 54 ×24 = 514 /104
= 0.0514
So, 0.0514 is the required decimal expansion of the rational number 257/ 5000

Question. Three bells toll at intervals of 12 minutes, 15 minutes and 18 minutes respectively, if they start tolling together, after what time will they next toll together?
Solution. The required time is the LCM of 12, 15 and 18.
12 = 2 × 2 × 3
15 = 3 × 5
18 = 2 × 3 × 3
LCM = 2² × 3² × 5 = 180
So, next time the bells will ring together after 180 minutes or 3 hours.

Question. Find if 987/ 10500 will have terminating or non– terminating (repeating) decimal expansion.
Give reasons for your answer.
Solution. Yes, it will have a terminating decimal expansion.
Simplified denominator has factor in the form of 2^m × 5ⁿ.
Now, 987/ 10500 = 3×7×47/ 2×2×3×5×5×5×7
= 47/ 5³ 2² × 2/2 = 94/5³2³
94/ 1000
= 0.094
And we know, if p/q is a rational number, such that the prime factorization of q is of the form 2^m × 5ⁿ where n and m are non–negative integers, than x has a decimal expansion which
terminates.
Hence, it terminates.

Question. A merchant has 120 litres and 180 litres of two kinds of oil. He wants to sell oil by filling the two kinds of oil in tins of equal volumes. What is the greatest volume of such a tin?
Solution. In order to find volume of such a tin, we need to find the largest number which exactly divides 120 and 180 which is nothing but the HCF (120, 180).
120 = 2 × 2 × 2 × 3 × 5
180 = 2 × 2 × 3 × 3 × 5
H.C.F. (120, 180) = 2 × 2 × 3 × 5 = 60
Hence, the greatest volume of each tin is 60 litres

Question. A rational number in its decimal expansion is 327.7081. What can you say about the prime factors of q, when this number is expressed in the form p ? Give reasons. 
Solution. As 327.7081 is a terminating decimal number, the denominator of the rational number must be of the form 2^m × 5ⁿ.
Thus, 327.7081 = 10000 /3277081
= 3277081/ 10⁴
= 3277081/ 2⁴× 5⁴ = p/q
So, the prime factors of q are 2 and 5. Here, q is of the form 2m × 5n, where m and n are natural numbers. The prime factors of p and q will be either 2 or 5 or both.

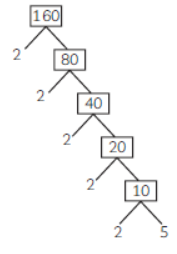
Question. In the adjoining factor tree, find the numbers m and n. 

Solution. Here, m = 160 and n = 40

Question. Without actually performing the long division, write the decimal expansion of 11725/ 2³ × 5 ⁴ .
Solution. 11725/ 2³ × 5 ⁴ = 11725 ÷ 5/ 2³ × 5³ = 2345/ (10 )³ = 2.345

Question. Write any two irrational numbers whose product is a rational number.
Solution. Consider two irrationals as, 5 − 2 √2 and 5 + 2 √2
Here,
(5 − 2 √2)(5 + 2 √2) = 5² − (2 √2)²
= 25 – 8 = 17 (a rational number)

Question. Prove that 3 + 2 √5 is irrational number.
Solution. Let 3 + 2 √5 be a rational number.
So we can write this number as
3 + 2 √5 = a/ b
Here a and b are two co-prime integers and b ≠ 0.
Subtracting 3 from both sides, we get
2 √5 = a/ b – 3
2 √5 = (a − 3b) b 
On dividing both sides by 2, we get
√5 = (a – 3b)/2b
Here a and b are integers, so (a – 3b)/2b is a rational number which implies 5 should be a rational number, but √5 is an irrational number so it is a contradiction.
Hence, 3 + 2 √5 is an irrational number.

Question. Show that 5+2 √7 is an irrational number, where √7 is given to be an irrational number. 
Solution. Let us assume, on the contrary, that 5+2 √7 is a rational number.
i.e., 5+2 √7 = a/ b ,
where ‘a’ and ‘b’ are co-prime numbers.
⇒ 2 √7 = a/ b −5
⇒ √7 = a – 5b/2b 
Since a – 5b/ 2b is a rational number, √7 is also a rational number, which is contradiction to the given results.
Hence, 5+2 √7 is irrational.

Question. Prove that 2 + 5 √3 is an irrational number, given that 3 is an irrational number. 
Solution. Let us assume that 2 + 5 √3 is a rational number.
Therefore: 2 + 5 √3 = a/ b
(where, ‘a’ and ‘b’ are co-primes)
⇒ 5 √3 = a – 2b/b
⇒ 5 √3 = a b / b 
⇒ √3 = a – 2b / 5b
Therefore, a- 2b/ 5b is in the form of a b which is a rational number.
But, this contradicts the fact that √3 is an irrational number.
Therefore, our assumption is wrong and 2 + 5 √3 is an irrational number.

Question. Prove that one of every three consecutive positive integers is divisible by 3. 
Solution. Let n, n + 1 and n + 2 be three consecutive positive integers Also, we know that a positive integer n is of the form 3q, 3q + 1 or 3q + 2
Case I: When n = 3q Here n is clearly divisible by 3.
But ( n + 1) and (n + 2) are not divisible by 3.
[When (n + 1) is divided by 3, remainder is 1 and when (n + 2) is divided by 3, the remainder is 2]
Case II: When n = 3q + 1
Here n + 2 = 3q + 3 = 3(q + 1)
Clearly, it is divisible by 3. But n and (n + 1) are not divisible by 3.
Case III: when n = 3q + 2
Here, n + 1 = 3q + 3 = 3(q + 1)
clearly, (n + 1) is divisible by 3
But n and (n + 2) are not divisible by 3
Hence, one of every three consecutive positive integers is divisible by 3.

Question. Prove that n is not a rational number, if n is not perfect square.
Solution. Let √n be a rational number.
Let  √n =  where p and q are co-prime integers, q ≠ 0.
On squaring both sides, we get
⇒ n = p²/q²
          p² = nq²
⇒ n divides p²
[Let p be a prime number. If p divided a2 then p divides a, where a is a positive integer]
⇒ n divides p …(ii)
Let p = nm, where m is any integer.
⇒ p² = n² m²
(i) ⇒ n² m² = nq²
⇒ q² = nm²
⇒ n divides q²
⇒ n divides q …(iii)
[Let p be a prime number. If p divided a² then p divides a, where a is a positive integer] From (ii) and (iii), n is a common factor of both p and q which contradicts the assumption that p and q are co-prime integer.
So, our supposition is wrong, √n is an irrational number.

Question. Show that the square of any positive integer cannot be of the form (5q + 2) or (5q + 3) for any integer q. 
Solution. Let ‘a’ be any positive integer. Then, it is of the form 5p, or 5p + 1 or 5p + 2 or 5p + 3 or 5p + 4
Case 1 When a = 5p
⇒ a² = 25p² = 5(5p²) = 5q, where q = 5p²
Case 2 When a = 5p + 1
⇒ a2 = 25p² + 10p + 1= 5(5p² + 2p) + 1 = 5q +
1, where q = 5p² + 2p.
Case 3 When a = 5p + 2
⇒ a² = 25p² + 20p + 4= 5(5p² + 4p) + 4 = 5q + 4, where q = 5p² + 4p.
Case 4 When a = 5p + 3
⇒ a² = 25p² + 30p + 9= 5(5p² + 6p + 1) + 4
= 5q + 4, where q = 5p² + 6p.
Case 5 When a = 5p + 4
⇒ a² = 25p² + 40p + 16= 5(5p² + 8p + 3) + 1
= 5q + 1, where q = 5p² + 8p +
Thus, square of any positive integer cannot be of the form 5q + 2 or 5q + 3, for any integer n.

Question. The decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write it in the form p/ q · What can you say about the prime factors of q?
(A) 0.140140014000140000 …
(B) 0.16
Solution. (A) We have, 0.140140014000140000… a nonterminating and non-repeating decimal expansion. So it is irrational. It cannot be
written in the form of p/ q ·
(B) We have, ¯0.16 a non-terminating but
repeating decimal expansion. So it is
rational.
Let x = 0.16
Then, x = 0.1616… …(i)
100x = 16.1616 …(ii)
On subtracting (i) from (ii), we get
100x – x = 16.1616 – 0.1616
⇒ 99x = 16 ⇒ x = 16/ 99
The denominator (q) has factors other than 2 or 5.

Practice Exercise

Question. Is (5 + √3)² + (5 – √3)² is a rational number? Justify.
Solution. yes

Question. Two tankers contains 850 litres and 680 litres of petrol respectively. Find the maximum capacity of a container which can measure the petrol of either tanker in exact number of times.
Solution. 170 litres

Question. Write the rational number 5/6 in decimal form.
Solution. 0.⁻83

Question. Use Euclid’s division algorithm to find HCF of 867 and 255.
Solution. 51

Question. Find the HCF and LCM of 144, 180 and 192 by prime factorisation method.
Solution. LCM = 2880, HCF =12

Question. Find the LCM and HCF of 26 and 91.
Solution. LCM = 182, HCF = 13

Question. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion :
(i) 7/13   (ii) 131/420  (iii) 23/500  (iv) 131/23 x 52 x 7  (v) 134/2500
Solution. (i) non-terminating repeating
(ii) non-terminating repeating
(iii) Terminating
(iv) non-terminating repeating
(v) Terminating

Question. Write 504 as a product of its prime factors.
Solution. 2³ × 3² × 7

Question. The length, breadth and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm respectively. Determine the length of largest rod which can measure the three dimensions of the room exactly.
Solution. 75 cm

Question. Check whether 8n can end with the digit zero for any natural number n.
Solution. No

Question. A merchant has 105 litres of oil of one kind, 140 litres of another kind and 175 litres of third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?
Solution. 35

Question. Find the LCM and HCF of the following pairs of integers and verify that LCM× HCF = Product of the integers.
(i) 63 and 168 (ii) 144 and 160 (iii) 510 and 92 (iv) 252, 488
Solution. (i) LCM = 504, HCF = 21 (ii) LCM = 1440, HCF = 16 (iii) LCM = 23460, HCF = 2
(iv) LCM = 30744, HCF = 4

Question. Using Euclid’s division algorithm, find the HCF of :
(i) 210 and 55 (ii) 117 and 65 (iii) 240 and 1024
(iv) 391 and 425 (v) 1288 and 575 (vi) 155 and 1385
Solution. (i) 5 (ii) 13 (iii) 16 (iv) 17 (v) 23 (vi) 5

Question. Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where m, n are non-negative integers :
(i) 5/8 (ii) 17/125 (iii) 13/80 (iv) 123/625 (v) 7014/400 (vi) 17/2000
Solution. (i) 0.625 (ii) 0.136 (iii) 0.1625
(iv) 0.1968 (v) 17.535 (vi) 0.0085

Question. Find the largest number which exactly divides 280 and 1245 leaving remainders 4 and 3, respectively.
Solution. 138    

Question. Find the LCM and HCF of the following integers by applying the prime factorisation method :
(i) 12, 15 and 21 (ii) 15, 24 and 36 (iii) 225, 336 and 360 (iv) 240, 1024, 1536
Solution. (i) LCM = 420, HCF = 3 (ii) LCM = 360, HCF = 3 (iii) LCM = 25200, HCF = 3
(iv) LCM = 15360, HCF = 16

Question. The HCF and LCM of two numbers are 12 and 240 respectively. If one of these numbers is 48, find the other number.
Solution. 60

Question. In a seminar, the number of participants in Hindi, English and Mathematics are 60, 84 and 108, respectively. Find the minimum number of participants are to be seated and all of them being in the same subject.
Solution. 21

Question. Express each of the following positive integers as the product of its prime factors :
(i) 60 (ii) 1386 (iii) 6435
(iv) 2184 (v) 8085 (vi) 14850
Solution. (i) 22 × 3 × 5 (ii) 2 × 32 × 7 × 11 (iii) 32 × 5 × 11 × 13 (iv) 23 × 3 × 7 × 13
(v) 3 × 5 × 72 × 11 (vi) 2 × 33 × 52 × 11

Question. The product of two numbers is 20736 and their HCF is 54. Find their LCM.
Solution. 384

Question. The LCM of two numbers is 192 and their product is 3072. Find their HCF.
Solution. 16

Question. Find the HCF of 300, 540, 890 by using Euclid’s division algorithm.
Solution. 10

Question. Without actually performing the long division, state whether the following rational numbers will have terminating decimal expansion or a non-terminating repeating decimal expansion :
(i) 13/121 (ii) 57/128 (iii) 19/45 (iv 108/250 (v) 113/175 (vi) 517/2000
Solution. (i) non-terminating repeating (ii) terminating
(iii) non-terminating repeating (iv) terminating
(v) non-terminating repeating (vi) terminating

Assignments for Class 10 Mathematics Real Numbers as per CBSE NCERT pattern

All students studying in Grade 10 Mathematics Real Numbers should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Real Numbers exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Real Numbers which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.

Some advantages of Free Assignments for Class 10 Mathematics Real Numbers

1. Solving Assignments for Mathematics Real Numbers Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
2. By solving one assignments given in your class by Mathematics Real Numbers teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
3. You will be able to understand the type of questions which are expected in your Mathematics Real Numbers class test
4. You will be able to revise all topics given in the ebook for Class 10 Mathematics Real Numbers as all questions have been provided in the question banks
5. NCERT Class 10 Mathematics Real Numbers Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
6. Parents will be able to take print out of the assignments and give to their child easily.

All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Real Numbers teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Real Numbers Assignments PDF.