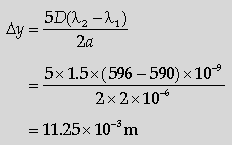Please refer to Wave Optics Class 12 Physics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Physics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Physics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.
Class 12 Physics Important Questions Wave Optics
Very Short Answer Type Questions
Question. What is the phase difference between two points on the same wavefront?
Answer. Phase difference between two points on the same wavefront is zero.
Question. What is the type of wavefront generated from
(a) Line source
(b) Point source?
Answer. (a) Cylindrical wavefront is generated from a line source.
(b) Spherical wavefront is generated from a near point source. Plane wavefront is generated from a far away point source.
Question. Can Huygen’s theory explain the photoelectric effect?
Answer. No, Huygen’s theory cannot explain the photoelectric effect.
Question. When a wave undergoes reflection at an interface from rarer to denser medium, what is the adhoc change in its phase?
Answer. The adhoc change in its phase is π.
Question. A plane wavefront is incident on a convex lens.
What will be the shape of the wave front emerging from the lens ?
Answer. Emerging wavefront will be spherical.
Question. A point source is kept at the focus of a concave mirror. The spherical wavefront emitted by the source get reflected by the mirror. What is the shape of the reflected wavefronts ?
Answer. Reflected wavefronts are plane wavefronts.
Question. In a Young’s double-slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter.
What will be the change in interference fringes ?
Answer. For sustained interference, the source must be coherent and should emit the light of same frequency.
In this problem, one hole is covered with red and other with blue, which has different frequency, so no interference takes place.
Question. Two coherent monochromatic light beams of intensities I and 4I superimpose.
What will be the maximum and minimum intensities ?
Answer.
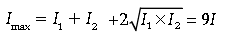
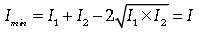
Question. The ratio of intensities of two waves is 1: 25, what is the ratio of their amplitudes?
Answer. 1: 5
Question. Why does the intensity of the secondary maximum become less as compared to the central maximum?
Answer. Since, the intensity of nth order maximum is inversely proportional to n, the secondary maximum is less bright as compared to the central maximum.
Short Answer Type Questions-I
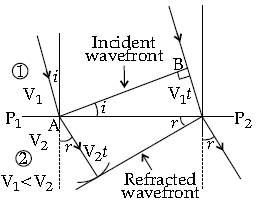
Question. Define the term ‘wavefront of light’. A plane wave front AB propagating from denser medium
(1) into a rarer medium (2) is incident on the surface P1P2 separating the two media as shown in fig.
Using Huygen’s principle, draw the secondary wavelets and obtain the refracted wavefront in the diagram.
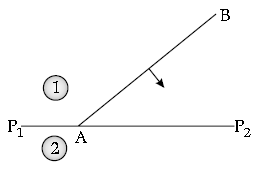
Answer. Wavefront: Wavefront is an imaginary surface over which an optical wave has a constant phase.
Refraction of light from denser medium to rarer medium:
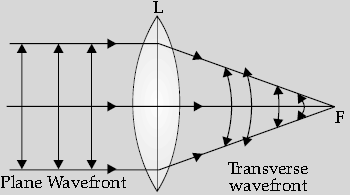
Question. Based on Huygens construction, draw the shape of a plane wavefront as it gets refracted on passing through a convex lens.
Answer.
Question. Define secondary wavelets and how can we construct new wavefront with them ?
Answer. According to the Huygens’ principle, every particle of the medium, situated on the wavefront, acts as a new source of light wave from which new similar waves originate. These waves are called secondary wavelets.
The envelop of the secondary wavelets in the forward direction at any instant gives the new wavefront at that instant.
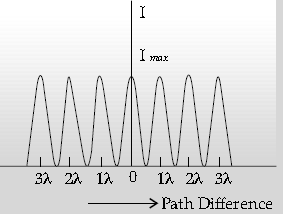
Question. Draw the graph showing intensity distribution of fringes with phase angle due to diffraction through single slit.
Answer. Plot of Intensity distribution of diffraction with proper labelling.
Question. What should be the width of each slit to obtain n maxima of double slit pattern within the central maxima of single slit pattern?
Answer. Let the width of each slit be a The separation between m maxima in a double slit experiment = ym

Question. In a single slit diffraction experiment, width of the slit is increased. How will the (a) size and (b) intensity of central bright band be affected? Justify your answer.
Ans. The width of the central bright band = 2D×λ/d
where d = width of the slit.
(i) As the width of the slit is doubled, the size of the central diffraction band will be half.
(ii) Intensity of central bright band is proportional to d2.
So, the intensity will get quadrupled.
Question. Draw the intensity pattern for single slit diffraction and double slit interference. Hence, state two differences between interference and diffraction patterns.
Answer.
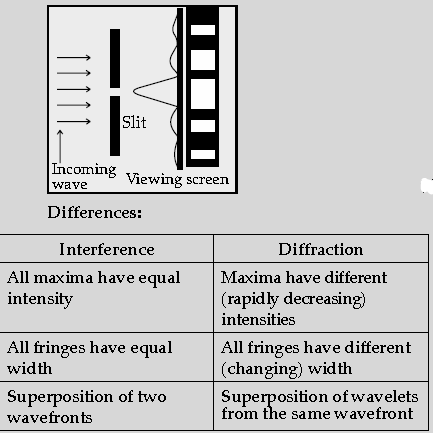
Question. A narrow slit is illuminated by a parallel beam of monochromatic light of wavelength l equals to 6000 Å and the angular width of the central maxima in the resulting diffraction pattern is measured. When the slit is next illuminated by light of wavelength λ’, the angular width decreases by 30%. Calculate the value of the wavelength λ’.
Answer. Angular width, 2q = 2λ/d
Given, λ = 6000 Å
In case of new wavelength (assumed λ’ here), angular width decreases by 30%
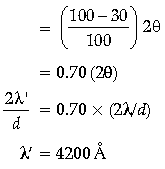
Question. A parallel beam of light of 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minima is at a distance of 2.5 mm from the centre of the screen. Calculate the width of the slit.
Answer. The distance of the 1st minima from the centre of the screen is,
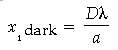
where, D = Distance of slit from screen,
λ = Wavelength of the light,
a = Width of the slit. ½
According to question,
D = 1 m
λ = 500 nm
height of first minima = 2.5 mm

Short Answer Type Questions-II
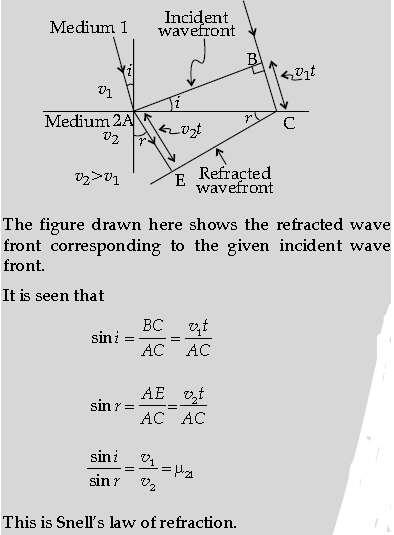
Question. Define the term, “refractive index” of a medium.
Verify Snell’s law of refraction when a plane wavefront is propagating from a denser to a rarer medium.
Ans. Definition of the refractive index Verification of laws of refraction
The refractive index of medium 2, with respect to medium 1 is equal to the ratio of the sine of angle of incidence (in medium 1) to the sine of angle of refraction (in medium 2).
Alternatively,
Refractive index of medium 2 w.r.t. medium
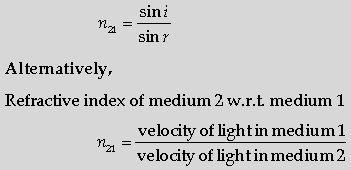
Question. (a) Compare Maxwell’s electromagnetic theory with Huygens wave theory of light.
(b) Define incident angle of a light wave.
Ans. (a) Both theories treat light as a wave in nature. However, as per the electromagnetic theory, light does not need any medium to propagate while for Huygens’ wave theory, a medium is must. That is why, he assumed a hypothetical medium ‘ether’ through which light wave travels in vacuum.
(b) Angle between incident wavefront with the interface is called the incident angle of light wave.
Question. (a) If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
(b) What kind of fringes do you expect to observe if white light is used instead of monochromatic light?
Ans. (a) Finding the (modified) ratio of the maximum and minimum intensities 2
(b) Fringes obtained with white light 1
(a) After the introduction of the glass sheet
(say, on the second slit),

(b) The central fringe remains white.
No clear fringe pattern is seen after a few (coloured) fringes on either side of the central fringe.
[Note: For part (a) of this question, The student may
(i) Just draw the diagram for the Young’s double slit experiment.
OR
(ii) Just state that the introduction of the glass sheet would introduce an additional phase difference and the position of the central fringe would shift.
For all such answers, the student may be awarded the full (2) marks for this part of this question.
Long Answer Type Questions
Question. (a) State the essential conditions for diffraction of light.
(b) Explain diffraction of light due to a narrow single slit and the formation of pattern of fringes on the screen.
(c) Find the relation for width of central maxima in terms of wavelength ‘l’, width of slit ‘a’, and separation between slit and screen ‘D’.
(d) If the width of the slit is made double the original width, how does it affect the size and intensity of the central band ?
Answer. (a) Size of slit/aperture must be smaller than that of the order of wavelength of light
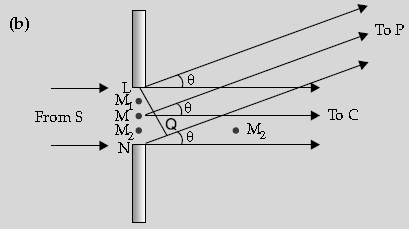
Single slit diffraction is explained by treating different parts of the wavefront at the slit as sources of secondary wavelets. At the central point C on the screen, θ is zero. All path differences are zero and hence all the parts of the slit contribute in phase and give maximum intensity at C.
At any other point P, the path difference between two edges of the slit is
NP – LP = NQ.
= asin θ » aθ sin θ is small
Any point P, in direction θ, is a location of minima
if aθ = nλ
This can be explained by dividing the slit into even number of parts. The path difference between waves from successive parts is 180° out of phase and hence cancel each leading to a minima.
Any point P, in direction Q, is a location of maxima

This can be explained by dividing the slit into odd number of parts. The contributions from successive parts cancel in pairs because of 180° phase difference. The unpaired part produces intensity at P, leading to a maxima.
(c) If θ is the direction of first minima, then

Question. (a) Why cannot the phenomenon of interference be observed by illuminating two pin holes with two sodium lamps ?
(b) Two monochromatic waves having displacements y1 = a cos ωt and y2 = a cos (ωt + j) from two coherent sources interfere to produce an interference pattern. Derive the expression for the resultant intensity and obtain the conditions for constructive and destructive interference.
(c) Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2 × 10–6 m. If the distance between the slit and the screen is 1.5 m calculate the separation between the positions of the second maxima of diffraction pattern obtained in the two cases.
Answer. • Reason
• Deriving the expression for resultant intensity and condition for constructive and destructive interference
• Calculating the separation
(a) Because two independent sources cannot be coherent OR they are not coherent.
(b) y1 = acos ωt
y2 = acos (ωt +φ)
So resultant displacement is give by
y = y1 + y2
y = acos ωt + acos (ωt + φ)
y = 2acos (φ/2) cos(ωt + φ/2)
The amplitude of the resultant displacement is 2acos(φ/2) and therefore intensity at that point will be I = 4I0 cos2 (φ/2)
For constructive interference:
f = 0,± 2p,± 4p ,…….
For destructive interference:
f = 0,± p, ± 3p,± 5p ,…….
(c) Position of second maxima,