Please refer to Polynomials Class 9 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 9 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 9 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 9.
Class 9 Mathematics Important Questions Polynomials
Very Short Answer Type Questions:
Question. Find p (0) if p (y) = y2 – y + 1.
Ans. Given, p (y) = y2– y + 1
∴ p (0) = 02 – 0 + 1 = 1
Question. Name the polynomial containing two non−zero terms.
Ans. Binomial.
Question. What is the degree of the polynomial (x3+ 5)(4 – x5) ?
Ans. Degree of x3+ 5 = 3
Degree of 4 – x5 = 5
Degree of (x3– 5)(4 – x5 ) = 3 + 5 = 8.
Question. Factorize : 6 – x – x2
Ans. 6 – x – x2= 6 – 3x + 2x – x2
= 3(2 – x) + x(2 – x)
= (2 – x)(3 + x)
Question. If –4 is a zero of the polynomial p(x)= x2 + 11x + k, then calculate the value of k.
Ans. Given, p(x) = x2 + 11x + k
Since, – 4 is a zero of polynomial
p(–4) = 0
or, (– 4)2 + 11 × (– 4) + k = 0
or, 16 – 44 + k = 0
∴ k = 28
Question. Write the number of zeroes in a cubic polynomial.
Ans. No. of zeroes of cubic polynomial = 3.
Question. Name the given polynomial on the basis of degree. – 3x + 2.
Ans. Linear polynomial.
Question. If p(x) = x2 – 3x + 2, then what is the value of p(0) + p(2) ?
Ans. Putting, x = 0
p(0) = 0 – 3 × 0 + 2 = 2
Putting, x = 2
p(2) = 22 – 3 × 2 + 2
= 4 – 6 + 2 = 0
Thus, p(0) + p(2) = 2 + 0 = 2
Question. What is the degree of polynomial 3 ?
Ans. Degree of polynomial is 0.
Short Answer Type Questions:
Question. If f(x) = x4 – 4x3 + 3x2 – 2x + 1, then find whether f(0) × f(– 1) = f(2).
Ans. Given, f(x) = x4 – 4x3 + 3x2 – 2x + 1
∴ f(0) = 1
and f(– 1) = (– 1)4 – 4(– 1)3 + 3(– 1)2 – 2(– 1) + 1
= 1 + 4 + 3 + 2 + 1 = 11
and f(2) = (2)4 – 4(2)3 + 3(2)2 – 2(2) + 1 1
= 16 – 32 + 12 – 4 + 1
= 29 – 36 = – 7
∴ f(0) × f(– 1) = 11 ≠ f(2)
Question. Factorize : 64a3 – 27b3 – 144a22b + 108ab2
Ans. 64a3 – 27b3 – 144a2b + 108ab2
= (4a)3 – (3b)3 – 3 × (4a)2 × (3b) + 3 × (4a) × (3b)2
= (4a)3 – (3b)3 – 3 × 4a × 3b(4a – 3b)
= (4a – 3b)3
Question. If f(x) = x3 – 3x2 + 3x – 4, find f(2) + f(– 2) + f(0).
Ans. Given, f(x) = x3 – 3x2 + 3x – 4
∴ f(2) = (2)3 – 3(2)2+ 3(2) – 4
= 8 – 12 + 6 – 4
f(2) = – 2
and f(– 2) = (– 2)3 – 3(– 2)2 + 3(– 2) – 4
= – 8 – 12 – 6 – 4
f(– 2) = – 30
and f(0) = – 4
∴ f(2) + f(– 2) + f(0) = – 2 – 30 – 4 = – 36
Question. If f(x) = 5x2 – 4x + 5, find f(1) + f(– 1) + f(0).
Ans. Given, f(x) = 5x2 – 4x + 5
∴ f(1) = 5 – 4 + 5
= 6
and f(– 1) = 5(– 1)2 – 4(– 1) + 5
= 5 + 4 + 5 = 14
and f(0) = 5
∴ f(1) + f(– 1) + f(0) = 6 + 14 + 5 = 25
Question. Evaluate : ( √2 + √3) ( √5 − √2) + 2 + − 2
Ans. ( √2 + √3)2 ( √5 − √2)2 = (√2)2 + (√3)2 + 2 × √2 × √3 + (√5)2 + (√2)2 − 2 × √5 × √2
= 2 + 3 + 2√6 + 5 + 2 – 2√10
= 12 + 2√6 − 2√10
= 2(6 + √6 − √10 )
Question. Find the value of the polynomial p(x) = x3– 3x2 – 2x + 6 at x = √2
Ans. Given, p(x) = x3– 3x2 – 2x + 6
Then, p(√2) = (√2)3 − 3(√2 )2 − 2(√2) + 6
= 2√2 − 6 − 2√2 + 6
= 0
Question. If x2 + 1/x2 = 7. Find the value of x3+ 1/x3, taking only the positive value of x + 1/x
Ans. (x + 1/x)2 = x2+ 1/x2 + 2.x.1/x
= x2+ 1/x2 + 2
= 7 + 2 [∴ x2+ 1/x2 = 7 ]
= 9
x + 1/x = ± 3
x + 1/x = 3 [on taking +ve value]
Now, x3+ 1/x3= (x + 1/x)(x2 + 1/x2 − x.1/x)
= (x + 1/x)(x2 + 1/x2 − 1)
= (3)(7 − 1)
= 3 x 6 = 18
Question. Factorize : 2y3 + y2– 2y –1
Ans. 2y3 + y2– 2y – 1 = y2(2y + 1) – 1(2y + 1)
= (2y + 1)(y2 – 1)
= (2y + 1)(y – 1)(y + 1)
Question. If z2 + 1/z2 = 14. Find the value z3 + 1/z3 taking only positive value of z + 1/z
Ans. (z + 1/z)2 = z2 + 1/z2 + 2
= 14 + 2 = 16
z + 1/z = ±4
or, z3 + 1/z3= (z + 1/z)3 − 3(z + 1/z)
=(4)3 – 3(4)
= 64 – 12
or, z3+ 1/z3 = 52
Long Answer Type Questions:
Question. Using factor theorem, find the value of ‘a‘. If 2x4 – ax3 + 4x2 – x + 2 is divisible by 2x + 1.
Ans. Let p(x) = 2x4 – ax3 + 4x2 – x + 2
If (2x + 1) is a factor of p(x), then 2x + 1 = 0.
or, x = −1/2 is a zero of the polynomial p(x)
So, p(− 1/2) = 0
or 2 × (−1/2)4 −a(−1/2)3 + 4(−1/2)2 − (−1/2) + 2 = 0
or, 2 × (1/16) −a(−1/8) +4(−1/4) − (−1/2) + 2 = 0
or, 1/8 + a/8 +1 + 1/2 + 2 = 0
or, 29/8 + a/8 = 0
∴ a = – 29
Question. ab + bc + ca = 0, find the value of 1/a2− bc + 1/b2 − ca + 1/c2 − ac.
Ans. ab + bc + ca = 0 …(i)
⇒ – bc = ab + ca …(ii)
– ca = ab + bc …(iii)
and – ab = bc + ca …(iv)
Now, 1/a2− bc + 1/b2 − ca + 1/c2 − ac
= 1/ a2+ ab + ca + 2/b2 + ab + bc + 1/c2 + bc + ca [Using (i), (iii) & (iv)]
= 1/a(a + b + c) + 2/b(a + b + c) + 1/c(a + b + c)
= 1/a + b + c(1/a +1/ b +1/ c)
= bc + ca + ab/abc(a + b + c)
= 0
Question. Using factor theorem, show that (m – n), (n – p) and (p – m) are factors of m(n2 – p2) + n(p2 – m2) + p(m2 – n2)
Ans. Let f = m(n2 – p2 ) + n(p2 – m2) + p(m2 – n2 )
∴ f(m = n) = n(n2 – p2 ) + n(p2 – n2 ) + p(n2 – n2 )
= n(n2 – p2 ) – n(n2 – p2 ) + 0
= 0
So, m – n is a factor of f.
Similarly, f(n = p) = 0 & f(p = m)= 0
∴ (m – n), (n – p) and (p – m) are factors of f.
Question. Factorize : 9x3 – 3x2 – 5x – 1
Ans. Let p(x) = 9x3 – 3x2 – 5x – 1
Factors of 1 = ± 1
p(1) = 9 – 3 – 5 – 1 = 0
i.e., x – 1 is a factor of p(x).
∴ 9x3 – 3x2 – 5x – 1 = 9x2(x – 1) + 6x(x – 1) + 1(x – 1)
= (x – 1)(9x2 + 6x + 1)
= (x – 1)(3x + 1)2)2
∴ p(x) = (x – 1)(3x + 1)(3x + 1)
Question. Factorize : 1/64x3 − 8y3 + 3/16x2y − 3/2xy2
Ans.
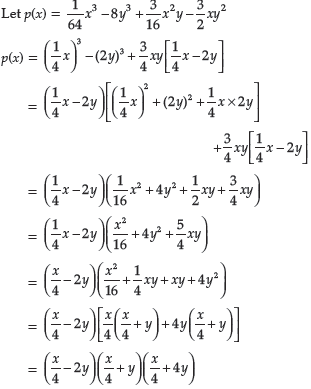
Question. If f(x) = x2– 5x + 7, evaluate f(2) – f(–1) + f(1/3)
Ans. Given, f(x) = x2– 5x + 7
Then, f(2) = 22 – 5 × 2 + 7 = 1
and f(–1) = (– 1)2 – 5 (–1) + 7 = 13
and f(1/3) = (1/3)2 − 5(1/3) + 7 = −49/9
Thus, f(2) – f(–1) + f(1/3) = 1− 13 + 49/9 = −59/9
Question. Find the value of the polynomial x2– 3x + 6 at
(i) x = √2 , (ii) x = 3.
Ans. Given, p(x) = x2– 3x + 6
(i) When x = √2
Then, p(√2 ) = ( √2)2 − 3 × √2 + 6
= 2 – 3√2 + 6
= 8 – 3√2
(ii) When x = 3
Then, p(3) = 32 – 3 × 3 + 6
= 9 – 9 + 6
= 6


