Please refer to Dual Nature of Radiation and Matter Class 12 Physics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Physics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Physics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.
Class 12 Physics Important Questions Dual Nature of Radiation and Matter
Very Short Answer Type Questions
Question. In a photoelectric experiment, the potential required to stop the ejection of electrons from cathode is 4 V. What is the value of maximum kinetic energy of emitted Photoelectrons?
Answer. 4 eV
Question. Photons of frequency v are incident on the surface of two metals A and B of threshold frequencies 3 v/4 and 2 v/3 , respectively. Find the ratio of maximum kinetic energy of electrons emitted from A to that from B.
Answer.

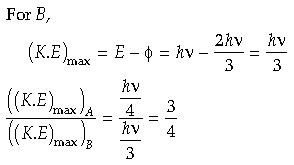
Question. If photons of frequency ν are incident on the surfaces of metals A and B of threshold frequencies v/2 and v/3 respectively. Find ratio of the maximum kinetic energy of electrons emitted from A and B.
Answer.
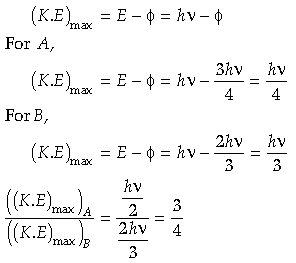
Question. A photocell connected in an electrical circuit is placed at a distance ‘d’ from a source of light. As a result, current I flows in the circuit. What will be the current in the circuit when the distance is reduced to d/3 ?
Answer. The current emitted in a photocell is inversely proportional to the distance of the source of light from the photosensitive device.
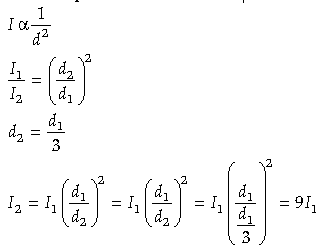
Question. State one factor which determines the intensity of light in the photon nature of light.
Answer. Number of photons emitted per second determines the intensity of light in the photon nature of light.
Question. Define the term “threshold frequency” in the context of photoelectric emission.
Answer. Threshold frequency equals the minimum frequency of incident radiation (light) that can cause photoemission from a given photosensitive surface. [Alternatively] The frequency below which the incident radiations cannot cause the photoemission from photosensitive surface.
Question. A photocell connected in an electrical circuit is placed at a distance ’d’ from a source of light. As a result, current I flows in the circuit. What will be the current in the circuit when the distance is increased to ‘2d’ ?
Answer. The current emitted in a photocell is inversely proportional to the square of the distance of the source of light from the photosensitive device

Question. Draw graphs showing variation of photoelectric current with applied voltage for two identical radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
Answer.

Question. How does the intensity affect the photoelectric current ?
Answer. As intensity increases the photoelectric effect. Since each incident photon ejects one photoelectron from a metal surface, therefore, the number of photoelectrons emitted depends on the number of photons falling on the metal surface, which in turn depends on the intensity of the incident light. Hence, as the intensity increases, the number of photoelectrons ejected increases and hence photoelectric current increases.
Question. Work function of lithium is 2.5 eV. What will be the maximum wavelength of light that can cause the photoelectric effect ion lithium?
Answer. By photoelectric effect,

Question. Light of wavelength 3500 Å is incident on two metals A and B. Which metal will yield more photoelectrons if their work functions are 5 eV and 2 eV respectively?
Answer. Metal B will yield more photo electrons. work function of Metal B is lower than that of A for the same wavelength of light. Hence metal B will give more electrons
Question. Define the term “Intensity” in photon picture of electromagnetic radiation.
Answer. Intensity of radiation is proportional to (equal to) the number of energy quanta (photons) per unit area per unit time.
Question. Name the phenomenon which shows the quantum nature of electromagnetic radiation.
Answer. Photoelectric effect (Raman / Compton effect)
Question. If the distance between the source of light and the cathode of a photocell is doubled, how does it affect the stopping potential applied to the photocell ?
Answer. It does not affect the stopping potential as stopping potential only depends upon the frequency of light.
Question. The graph below is produced when monochromatic light is shown onto a metal surface. The frequency of the light is slowly increased. The maximum kinetic energy of any emitted electrons is plotted on the y-axis.

(a) What is the point B called?
(b) What quantity is given by the gradient ΔEk/Δf of this graph?
Answer. (a) Threshold frequency
(b) Planck’s constant (h)
Question. A proton and an α-particle are accelerated by the same potential difference. Find the ratio of their de broglie’s wavelengths (λo,λu)
Answer.
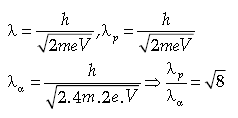
Question. Find the ratio of de-Broglie wavelengths associated with two electrons accelerated through 25 V and 36 V.
Answer. V1 = 25 V, V2 = 36 V
de-Broglie wavelength of an electron
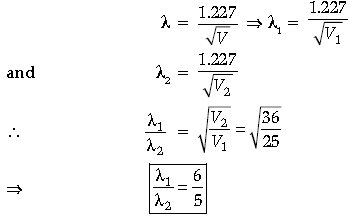
Question. Draw a graph to show the variation of particle momentum and associated de-Broglie wavelength?
Answer. Since

Question. If K.E. of free electron is doubled, what will be the change in wavelength?
Answer.
Question. The work function of caesium metal is 2.14 eV.
When light of frequency 6 × 1014 Hz is incident on the metal surface, photoemission of electrons occurs. What is the maximum kinetic energy of the emitted electrons?
Answer. The maximum kinetic energy is given by the photoelectric effect as:
K = (hν – Φ0)
Where, h = Planck’s constant = 6.626 × 10−34 Js

Hence, the maximum kinetic energy of the emitted electrons is 0.345 eV.
Question. Threshold wavelength for a metal having work function W0 is X. What is the threshold wavelength for the metal having work function 2W0 ?
Answer. Since

Question. Which phenomenon best supports the theory that matter has a wave nature?
Answer. Diffraction.
Question. Draw a plot showing the variation of de-Broglie wavelength of electron as a function of its K.E
Answer.

Question. Two particles have equal momenta. What is the ratio of their de-Broglie wavelengths?
Answer. P1 = P2
ratio λ1/λ2 = 1: 1
Short Answer Type Questions-I
Question. In case of photoelectric effect experiment, explain the following facts, giving reasons.
(a) The wave theory of light could not explain the existence of the threshold frequency.
(b) The photo electric current increases with increase in the intensity of incident light.
Answer. (a) Since energy of the wave is dependent on the square of its amplitude, the classical wave theory predicts that if sufficiently intense light is incident, the electrons would absorb that energy to escape. There should not be any threshold frequency for the emission of electrons from metal’s surface due to incident light.
(b) According to classical wave theory, if intensity of light increases, the kinetic energy of an ejected electron will increase. This is because the greater the intensity of light, the larger the energy of the light wave striking the metal surface, so electrons are ejected with greater kinetic energy. However,
it cannot explain the increase of number of ejected electrons i.e. the increase of photoelectric current, with the increase in intensity of incident light.
Question. Light of same wavelength is incident on three photo-sensitive surfaces A, B and C. The following observations are recorded.
(a) From surface A, photoelectrons are not emitted.
(b) From surface B, photoelectrons are just emitted.
(c) From surface C, photoelectrons with some kinetic energy are emitted.
Compare the threshold frequencies of the three surfaces and justify your answer.
Answer. (a) From surface A, electron is not emitted. So, the value of threshold frequency is less than the frequency of the incident radiation.
(b) From surface B, photoelectrons are just emitted.
So, the value of threshold frequency is equal to the frequency of the incident radiation.
(c) From surface C, photoelectrons are just emitted with some kinetic energy. So, the value of threshold frequency is more than the frequency of the incident radiation. Threshold frequency is defined as the minimum frequency of light which causes electron emission from a metal surface. No electron emission means that the frequency of the light is less than the threshold frequency and electron emission means that the frequency of the light is more than the threshold frequency.
Question. Figure shows the stopping potential (V0) for the photoelectron versus 1/λ graph, for two metals A and B, λ being the wavelength of incident light.
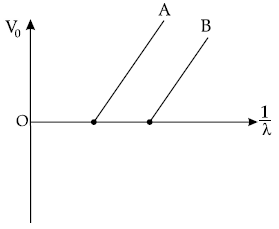
(a) How is the value of Planck’s constant determined from the graph ?
(b) If the distance between the light source and the surface of metal A is increased, how will the stopping potential from electrons emitted from it be effected ? Justify your answer.
Answer. (a) Planck’s constant can be determined from the gradient of the graph.
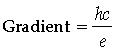
h = Planck’s constant
c = Velocity of light in vacuum
e = Charge of electron
Gradient to be measured from graph. The values of c and e are known. Hence, h can be determined.
(b) If distance between source of light and surface of metal A is increased, the intensity of incident light decreases. But stopping potential does not depend on the intensity of the incident light. So, the stopping potential will not be affected.
Question. A photon emitted during the de-excitation of electron from a state n to the first excited state in a hydrogen atom, irradiates a metallic cathode of work function 2 eV, in a photo cell, with a stopping potential of 0.55 V. Obtain the value of the quantum number of the state n.
Answer. • For writing Einstein’s photoelectric equation

Question. If the frequency of light incident on the cathode of a photocell is increased, how will following be affected ? Justify your answer.
(i) Energy of the photo electrons
(ii) Photo current A
Answer. If the frequency of light incident on the cathode of a photocell is increased, then 1
(i) energy of the photo electron increases as the energy of photon is directly proportional to the frequency.
(ii) rate of electron emission remains same. Hence, the current remains same.
Question. If light of wavelength 412.5 nm is incident on each of the metals given below, which ones will show photoelectric emission and why?

Answer. Calculating the energy of the incident photon Identifying the metals Reason.
The energy of a photon of incident radiation is given by
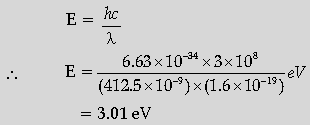
Hence, only Na and K will show photoelectric emission
Question. Using the graph shown in the figure for stopping potential V0 and the incident frequency of photons, calculate Planck’s constant.

Answer. Kinetic energy of an electron is calculated by,
K.E. = hv – ∅0
where work function
∅0 = hv0
where, n0 is cutoff frequency.
From the graph v0 = 5 × 1014 Hz
For frequency 8 ×1014 Hz; K.E. = eV0
So, at this frequency,

Question. Find the frequency of light which ejects electrons from a metal surface, fully stopped by a retarding potential of 3.3 V. If photo electric emission begins in this metal at a frequency of 8 × 1014 Hz, calculate the work function (in eV) for this metal.
Answer. Finding the work function
Finding the frequency of incident light
We have

Question. Why is wave theory of electromagnetic radiation not able to explain photoelectric effect? How does photon picture resolve this problem?
Answer. Reason for inability of E.M. theory Resolution through photon picture The explanation based on e.m. theory does not agree with the experimental observations (instantaneous nature, max K.E. of emitted photoelectron is independent of intensity, existence of threshold frequency) on the photoelectric effect.
[Note: Do not deduct any mark if the student does not mention the relevant experimental observation or mentions any one or any two of these observations].
The photon picture resolves this problem by saying that light, in interaction with matter behaves as if it is made of quanta or packets of energy, each of energy hν. This picture enables us to get a correct explanation of all the observed experimental features of photoelectric effect.
[ Note: Award the first mark if the student just writes “As per E.M. theory, the free electrons at the surface of the metal absorb the radiant energy continuously, this leads us to conclusions which do not match with the experimental observations”].
Also award the second mark if the student just writes “The photon picture give us the Einstein photoelectric equation
Kmax (= eV0) = hν – φ0
which provides a correct explanation of the observed features of the photoelectric effect.
Question. Monochromatic light of frequency 6.0 × 1014 Hz is produced by a laser. The power emitted is 2.0 × 10–3 W. Calculate the (i) energy of a photon in the light beam and (ii) number of photons emitted on an average by the source.
Answer. Calculating
(i) Energy of a photon
(ii) Number of photons emitted
Energy of photon = hn
= 6.63 × 10–34 × 6.0 × 1014 J
= 3.978 × 10–19 J
≅ 2.49 eV ½
Number of photons emitted per second

Question. The work function (W) of a metal X, equals 3 × 10–19 J. Calculate the number (N) of photons, of light of wavelength 26.52 nm, whose total energy equals W.
Answer.
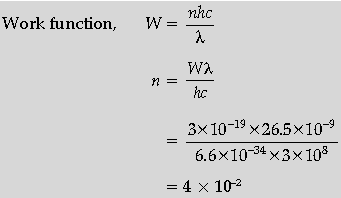
Question. Plot a graph showing variation of de Broglie wavelength (l) associated with a charged particle of mass m, versus 1/√V , where V is the potential difference through which the particle is accelerated. How does this graph give us the information regarding the magnitude of the charge of the particles ?
Answer. Plot of the graph showing the variation of

Question. Obtain the expression for the ratio of the de Broglie wavelengths associated with the electron orbiting in the second and third excited states of hydrogen atom.
Answer. 2πr = nλ
For second excited state (n = 3)
r = 0.529(n)2 Å
= 0.529(3)2
⇒ 2π(0.529)(3)2 = 3λ2
For third excited state, n = 4
r = 0.529 (4)2
⇒ 2p(0.529)(4)2 = 4λ3
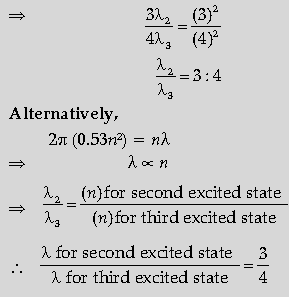
Question. An electron microscope uses electrons accelerated by a voltage of 50 kV. Determine the de-Broglie wavelength associated with the electrons. Taking other factors, such as numerical aperture etc. to be same, how does the resolving power of an electron microscope compare with that of an optical microscope which uses yellow light ?
Answer. de-Broglie wavelength of an electron

From the formula, it is clear that resolving power increases as wavelength decreases keeping other factors as constant.
Wavelength of yellow light = 680 nm = 6.8 × 10–7 m As we have seen from numerical calculation that electron wavelength is much lower than yellow light, hence resolving power of electronic microscope is much better than optical microscope.
Question. Calculate the de-Broglie wavelength of the electron orbiting in the n = 2 state of hydrogen atom.
Answer. Formulae of kinetic energy and de-Broglie a wavelength
Calculation and Result
Kinetic Energy for the second state-
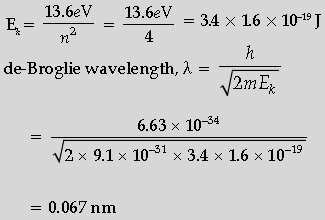
Question. Plot a graph showing variation of de-Broglie wavelength λ versus 1/√V, where V is accelerating potential for two particles A and B carrying same charge but of masses m1, m2 (m1 > m2). Which one of the two represents a particle of smaller mass and why?
Answer.

Hence, particle with lower mass (m2) will have greater slope.
Question. A proton and a deuteron are accelerated through the same accelerating potential. Which one of the two has:
(i) greater value of de-Broglie wavelength associated with it, and
(ii) less momentum ?
Give reasons to justify your answer.
Answer. (i) de-Broglie wavelength is given by
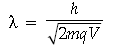
As mass of proton < mass of deuteron and qp = qd and V is same.
∴ λp > λd for same accelerating potential.

∴ Momentum of proton will be less than that of deuteron.
Short Answer Type Questions-II
Question. State Einstein’s photoelectric equation explaining the symbols used.

Light of frequency n is incident on a photosensitive surface. A graph of the square of the maximum speed of the electrons (n2max) vs. n is obtained as shown in the figure. Using Einstein’s photoelectric equation, obtain expressions for
(i) Planck’s constant. (ii) work function of the given photosensitive material in terms of parameters l, n and mass of the electron m.
Answer. Statement of equation with explanation of symbols
Expression for
(i) Planck’s constant
(ii) Work function
Einstein’s photoelectric equation is

hv = W0 + eVs
W = Work function of photosensitive material
Vs = Stopping Potential)
From Einstein’s photoelectric equation, we have
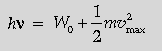
Question. State the main implications of observations obtained from various photoelectric experiments. Can these implications be explained by wave nature of light? Justify your answer.
Answer. Main implications:
Kinetic energy of emitted electrons depends upon frequency, but not on intensity of radiation.
There exist a frequency of radiation below which no photoemission takes place, how high intensity of radiation may be.
Explanation: wave nature of radiation fails to explain photoelectric effect.
Question. Using photon picture of light, show how Einstein’s photoelectric equation can be established. Write two features of photoelectric effect which cannot be explained by wave theory.
Answer. Photon picture plus Einstein’s photoelectric equation.
Two features
In the photon picture, energy of the light is assumed to be in the form of photons, each carrying an energy ℎν.
Einstein assumed that photoelectric emission occurs because of a single collision of a photon with a free electron.
The energy of the photon is used to:
(i) free the electrons from the metal.
[ For this, a minimum energy, called the work function (=W) is needed].
And
(ii) provide kinetic energy to the emitted electrons.
Hence

This is Einstein’s photoelectric equation Two features (which cannot be explained by wave theory):
(i) ‘Instantaneous’ emission of photoelectrons
(ii) Existence of a threshold frequency
(iii) ‘Maximum kinetic energy’ of the emitted photoelectrons, is independent of the intensity of incident light
Question. Write three characteristic features in photoelectric effect which cannot be explained on the basis of wave theory of light, but can be explained only using Einstein’s equation.
Answer. Three characteristic features The three characteristic features which can’t be explained by wave theory are:
(i) Kinetic energy of emitted electrons are found to be independent of intensity of incident light.
(ii) Below a certain frequency (threshold), there is no photo-emission.
(iii) Spontaneous emission of photo-electrons.
Question. In the study of a photoelectric effect the graph between the stopping potential V and frequency ν of the incident radiation on two different metals P and Q is shown below:

(i) Which one of the two metals has higher threshold frequency?
(ii) Determine the work function of the metal which has greater value.
(iii) Find the maximum kinetic energy of electron emitted by light of frequency 8 × 1014 Hz for this
Answer. (i) Q has higher threshold frequency
(ii) Work function, ∅0= hν0


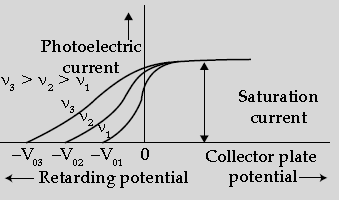
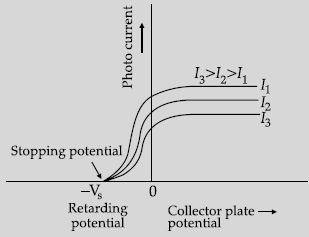
Question. The following graph shows the variation of photocurrent for a photosensitive metal:

(i) Identify the variable X on the horizontal axis.
(ii) What does the point A on the horizontal axis represent?
(iii) Draw this graph for three different values of frequencies of incident radiation ν1, ν2 and ν3(ν1 > ν2 > ν3) for same intensity.
(iv) Draw this graph for three different values of intensities of incident radiation I1, I2 and I3 (I1 > I2 > I3) having same frequency.
Answer. (i) X is collector plate potential.
(ii) A is stopping potential.
(iii) Graph for different frequencies:
(iv) Graph for three different Intensities:
Question. (i) How does one explain the emission of electrons from a photosensitive surface with the help of Einstein’s photoelectric equation?
(ii) The work function of the following metals is given: Na = 2.75 eV, K = 2.3 eV, Mo = 4.17 eV and Ni = 5.15 eV. Which of these metals will not cause photoelectric emission for radiation of wavelength 3300 Å from a laser source placed m away from these metals? What happens if the laser source is brought nearer and placed 50 cm away?
Answer. (i) Einstein’s Photoelectric equation is
hν = ∅o + Kmax
When a photon of energy ‘hν’ is incident on the metal, some part of this energy is utilized as work function to eject the electron and remaining energy appears as the kinetic energy of the emitted electron.

The work function of Mo and Ni is more than the energy of the incident photons; so photoelectric emission will not take place from these metals. Kinetic energy of photo electrons will not change, only photoelectric current will change.
Question. (i) State two features of Einstein’s photoelectric equation.
(ii) Radiation of frequency 1015 Hz is incident on two photosensitive surfaces P and Q. There is no photoemission from surface P. Photoemission occurs from surface Q but photoelectrons have zero kinetic energy. Explain these observations and find the value of work function for surface Q.
Answer. (i) Maximum kinetic (Kmax), of emitted electrons,
depends linearly on frequency of incident radiations
Kmax = hν – hν0
Existence of threshold frequency for the metal
surface ∅0 = hν0
(ii) Since no photoelectric emission takes place from P. It means frequency of incident radiation (1015 Hz) is less than its threshold frequency (ν0). Photo emission takes place from Q but kinetic
energy of photoelectrons is zero. This implies that frequency of incident radiation is just equal to the
threshold frequency of Q. For Q,
work function,
∅0 = hν0

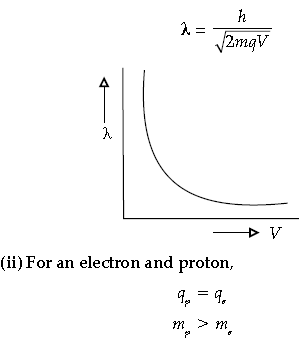
Question. (i) Draw the graph showing the variation of de-Broglie wavelength λ of a particle of charge q and mass m with the accelerating potential.
(ii) An electron and proton have the same de Broglie wavelengths. Explain, which of the two has more kinetic energy.
Answer. (i) Wavelength of a particle is given by

Question. Plot a graph showing the variation of photoelectric current with intensity of light. The work function for the following metals is given: Na: 2.75 eV and Mo: 4.175 eV. Which of these will not give photoelectron emission from a radiation of wavelength 3300 Å from a laser beam ? What happens if the source of laser beam is brought closer ?
Answer.

Question. Define the term “cut off frequency” in photoelectric emission. The threshold frequency of a metal is f. When the light of frequency 2f is incident on the metal plate, the maximum velocity of photo-electrons is v1. When the frequency of the incident radiation is increased to 5f, the maximum velocity of photo-electrons is v2. Find the ratio v1: v2.
Answer. Cut off frequency: It is that minimum frequency of incident radiation below which no photo emission takes place from a photo electric material.
(Alternatively, minimum frequency of incident radiation at which photons are just emitted with zero kinetic energy.)
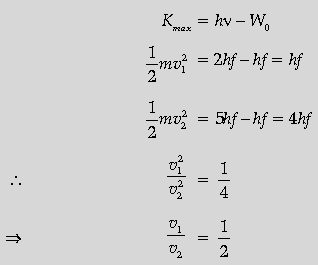
Long Answer Type Questions
Question. (i) Write three observed features of photoelectric effect which cannot be explained by wave theory of light. Explain how Einstein’s photoelectric equation is used to describe these features satisfactorily.
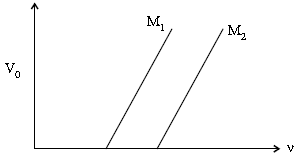
(ii) Figure shows a plot of stopping potential (V0) with frequency (n) of incident radiation for two photosensitive materials M1 and M2. Explain
(a) Why the slope of both the lines is same ?
(b) For which material emitted electrons have greater kinetic energy for the same frequency of incident radiation ?
Answer. (i) Three features of photoelectric effect, which cannot be explained by the wave theory of light, are:
(a) Maximum kinetic energy of emitted electrons is independent of the intensity of incident light.
(b) There exists a ‘threshold frequency’ for each photosensitive material.
(c) ‘Photoelectric effect’ is instantaneous in nature.
Einstein’s photoelectric equation,
K.E.max= hv – ∅0
[Alternatively: eV0 = hv – ∅0 ] can be used to explain
these features as follows.
(a) Einstein’s equation shows that Kmax∝ v.
However, Kmax does not depend on the intensity of light.
(b) Einstein’s equation shows that for v < ∅0/h, Kmax becomes negative, i.e, there cannot be any photoemission for v < v0
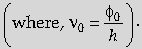
(c) The free electrons in the metal, that completely absorb the energy of the incident photons, get emitted instantaneously.
(ii) (a) Slope of the graph between V0 and n (from Einstein’s equation) equals (h/e). Hence, it does not depend on the nature of the material.
(b) Emitted electrons have greater energy for material M1. This is because ∅0 (= hv0) has a lower value for material M1.



