Chemical Kinetics  Class 12 Chemistry Important Questions

Please refer to Chemical Kinetics  Class 12 Chemistry Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Chemistry based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Chemistry for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.

Class 12 Chemistry Important Questions Chemical Kinetics 

Very Short Answer Questions

Question. If the rate constant of reaction is k = 3 × 10^–4s^–1, then identify the order of the reaction.
Answer. First order reaction.

Question. Define ‘order of a reaction’.
Answer. It is defined as “the sum of the powers or exponents to which the concentration terms are raised in the rate law expression.”
If rate = k[A]^m [B]ⁿ, then order = m + n.

Question. Identify the reaction order from the following rate constant :
k = 2.3 × 10^–5 L mol^–1s^–1 
Answer. Second order reaction :

Question. Distinguish between molecularity and order of a reaction.
Answer. Distinction between order and molecularity of a reaction :

Generally, in a complex reaction the order of reaction is equal to the molecularity of the slowest step.

Question. For the reaction, Cl_2(g) + 2NO_(g) → 2NOCl_(g) the rate law is expressed as Rate = k[Cl₂] [NO]₂
What is the overall order of this reaction?
Answer. Rate = k[Cl²] [NO]²
Hence order of the reaction = 1 + 2 = 3

Question. Express the rate of the following reaction in terms of disappearance of hydrogen in the reaction :
3H_2(g) + N_2(g) → 2NH_3(g)
Answer. 

Question. Define the half-life period of reaction (t½).
Answer. The time taken for half of the reaction to complete, i.e., the time in which the concentration of a reactant is reduced to half of its original value Is called half-life period of the reaction.

Question. If half-life period of a first order reaction is x and 3/4^th life period of the same reaction is y, how are x and y related to each other?
Answer. 

Question. For a reaction :

Rate = k
(i) Write the order and molecularity of this reaction
(ii) Write the unit of k.
Answer. (i) Rate = k
Experimentally, it is found that the rate of reaction is independent of the concentration of H₂ and Cl₂.
Hence, it is a zero order reaction. Molecularity = 2
(ii) Unit of k = mole litre^–1 sec^–1

Question. For a reaction A + B → P, the rate is given by Rate = k[A][B]²
(i) How is the rate of reaction affected if the concentration of B is doubled?
(ii) What is the overall order of reaction if A is present in large excess?
Answer. (i) From the rate law equation, order of reaction w.r.t. B is 2. Hence, if concentration of B is doubled, rate will become four times.
(ii) If A is present in large excess, rate of reaction will be independent of concentration of A and hence, order of reaction will be 2.

Question. Write units of rate constants for zero order and for the second order reactions if the concentration is expressed in mol L^–1 and time in second. 
Answer. Unit of rate constant (k), for zero order reaction.
Rate = k[A]⁰ ⇒ k = mol L^–1 s^–1
Unit of rate constant (k), for second order reaction
Rate = k[A]² ⇒ k = mol^–1 L s^–1

Question. Distinguish between ‘rate expression’ and ‘rate constant’ of a reaction.
Answer.  Rate expression is a way of expressing rate of reaction in terms of concentration of reactants, e.g.,
for a general reaction, aA + bB → cC + dD
Rate = k[A]^x [B]^y
Rate constant (k) is equal to the rate of reaction when molar concentration of reactant is unity. Its units depends upon the order of reaction.

Question. Rate constant k for a first order reaction has been found to be 2.54 × 10^–3 sec^–1. Calculate its 3/4th life. (log 4 = 0.6020)
Answer. The integrated rate equation for first order reaction is

Therefore, the 3/4^th life of the reaction is 546 seconds.

Question. The thermal decomposition of HCO₂H is a first order reaction with a rate constant of 2.4 × 10^–3 s–1 at a certain temperature. Calculate how long will it take for three-fourth of initial quantity of HCO₂H to decompose. (log 0.25 = – 0.6021)
Answer. For a first order reaction,

Question. In a first order reaction, the concentration of the reactant is reduced from 0.6 mol L^–1 to 0.2 mol L^–1 in 5 minutes. Calculate the rate constant of the reaction. 
Answer. a = 0.6 mol/L, (a – x) = 0.4 mol/L
t = 5 min

Question. How does a change in temperature affect the rate of a reaction? How can this effect on the rate constant of reaction be represented quantitatively?
Answer. The rate constant is nearly doubled with a rise in temperature by 10° for a chemical reaction. The temperature effect on the rate constant can be represented quantitatively by Arrherius equation :
k = Ae^–Ea/RT
where k → Rate constant
A → Arrhenius factor
R → Gas constant
T → Temperature
E_a → Energy of activation for the reaction

Question. The rate of most of the reactions becomes double when their temperature is raised from 298 K to 308 K. Calculate their activation energy.
[Given R = 8.314 J mol^–1 K^–1]
Answer. Here k₂ = 2k₁, T₁ = 298 K, T₂ = 308 K
E_a = ?

Short Answer Questions

Question. The decomposition of NH3 on platinum surface :

is a zero order reaction with k = 2.5 × 10^–4 mol L^–1 s^–1 What are the rates of production of N₂ and H₂?
Answer. The reaction is

Question. A first order reaction has a rate constant value of 0.00510 min^–1. If we begin with 0.10 M concentration of the reactant, how much of the reactant will remain after 3.0 hours?
Answer. Given : k = 5.10 × 10^–3 min^–1,
t = 3 × 60 min = 180 min
[R]₀ = 0.1 M
Substituting these values in the equation

Question. The half-life for a first order reaction is 5 × 10⁴ s. What percentage of the initial reactant will react in 20 hours? 
Answer. Here t_1/2 = 5 ×10⁴ s and t = 2 hours
= 2 × 60 × 60 = 7200 s

Question. A first order reaction is 20% complete in 5 minutes. Calculate the time taken for the reaction to be 60% complete.
Answer. For the first order reaction :

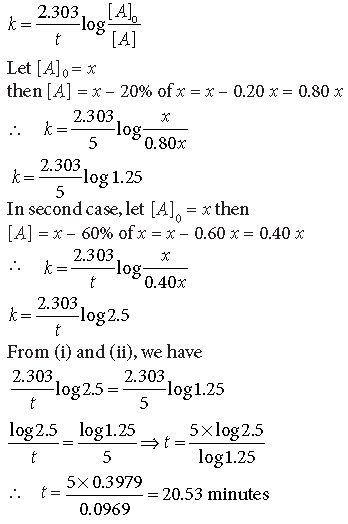
Question. The half-life for decay of radioactive 14C is 5730 years. An archaeological artifact containing wood has only 80% of the 14C activity as found in living trees. Calculate the age of the artifact
Answer. Radioactive decay follows first order kinetics.
Let [A]₀ = 100
∴ [A] = 100 × 80% = 80

Question. The rate constant for the first order decomposition of H₂O₂ is given by the following equation :

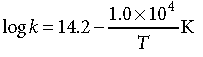
Calculate Ea for this reaction and rate constant k if its half-life period be 200 minutes.
(Given : R = 8.314 J K^–1 mol^–1)
Answer.

Question. The rate constant of a first order reaction increases from 2 × 10^–2 to 4 × 10^–2 when the temperature changes from 300 K to 310 K.
Calculate the energy of activation (E_a).
(log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
Answer. Given, T₁ = 300 K, T₂ = 310 K
k₁ = 2 × 10^–2, k₂ = 4 × 10^–2, Ea = ?
Using Arrhenius equation,

Question. The rate constants of reaction at 500 K and 700 K are 0.02 s^–1 and 0.07 s^–1 respectively.
Calculate the value of activation energy, E_a (R = 8.314 J K^–1 mol^–1).
Answer. k₁ = 0.02 s^–1, k₂ = 0.07 s^–1
T₁ = 500 K, T₂ = 700 K

Question. The rate of a reaction becomes four times when the temperature changes from 293 K to 313 K. Calculate the energy of activation (E_a) of the reaction assuming that it does not change with temperature.
[R = 8.314 J K^–1 mol^–1, log 4 = 0.6021]
Answer. Since the rate of a reaction quadruples when temperature changes from 293 K to 313 K.
∴ k₂ = 4k₁
T₁ = 293 K and T₂ = 313 K
According to Arrhenius equation

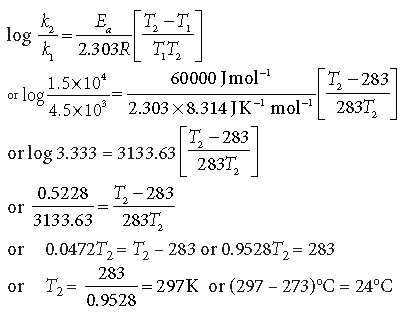
Question. The decomposition of A into products has a value of k as 4.5 × 10³ s^–1 at 10°C and energy of activation is 60 kJ mol^–1. At what temperature would k be 1.5 × 10⁴ s^–1?
Answer. k₁ = 4.5 × 10³ s^–1, T₁ = 10 + 273 K, k₂ = 1.5 × 10⁴ s^–1
T₂ = ? E_a = 60 kJ mol^–1
From Arrhenius equation,

Question. In general it is observed that the rate of a chemical reaction doubles with every 10 degree rise in temperature. If the generalisation holds good for a reaction in the temperature range 295 K to 305 K, what would be the value of activation energy for this reaction?
[R = 8.314 J/K^–1 mol^–1]
Answer. T₁ = 295 K, k₁ = k (say)
T₂ = 305 K, k₂ = 2k, E_a = ?
Using Arrhenius equation,

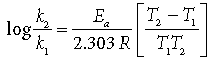
Question. The decomposition of phosphine,
4PH_3(g) → P4(g) + 6H_2(g)
has the rate law, Rate = k[PH₃].
The rate constant is 6.0 × 10^–4s^–1 at 300 K and activation energy is 3.05 × 10⁵ J mol^–1. Calculate
the value of rate constant at 310 K.
[Given : R = 8.314 J K^–1 mol^–1]
Answer. k₁ = 6.0 × 10^–4 s^–1, T₁ = 300 K, E^a = 3.05 × 10⁵ J mol^–1
k₂ = ?, T₂ = 310 K
Using Arrhenius equation,

Question. The first order rate constant for the decomposition of ethyl iodide by the reaction :
C₂H₅I_(g) → C2H_4(g) + HI^(g) at 600 K is 1.6 × 10^–5 s^–1. Its energy of activation is 209 kJ mol^–1.
Calculate the rate constant of reaction at 700 K.
Answer. Here T₁ = 600 K, T₂ = 700 K
E_a = 209 kJ/mol = 209000 J mol^–1
k₁ = 1.6 × 10^–5 s^–1
Using formula,

log k₂ – log (1.60 × 10^–5) = 2.598
log k₂ = 2.598 + log (1.6 × 10^–5)
log k₂ = – 4.796 + 2.598 = – 2.198
k₂ = Antilog (– 2.198)
or, k₂ = 6.34 × 10^–3 s^–1

Long Answer Questions

Question. With the help of a labelled diagram explain the role of activated complex in a reaction.
Answer. When the colliding molecules possess the kinetic energy equal to E_a, the atomic configuration of species formed at this stage is different from the reactant as well as the products. This stage is called the activated state and the specific configuration bearing state is called activated complex. For example, in the reaction between H_2(g) and I_2(g), activated complex has configuration in which H—H and I—I bonds are breaking and H—I bonds, are forming as shown below.

Question. A reaction is of second order with respect to its reactant. How will its reaction rate be affected if the concentration of the reactant is
(i) doubled
(ii) reduced to half ?
Answer. Let the concentration of the reactant [A] = a
Order of reaction = 2 so that
Rate of reaction = k [A]² …(1)
= ka²
(i) Given that concentration of the reactant is doubled So, that [A] = 2a,
Putting the value in equation (1) we get
New rate of reaction, R1
= k(2a)² = 4ka²
Hence, rate of reaction will increased to 4 times.
(ii) Given that concentration of the reactant is reduced to half
So that [A] = (1/2)a
Putting the value in equation (1), we get
New rate of reaction R² = k((1/2)a)²
= (1/4)ka²
Hence, rate of reaction will reduced to 1/4.

Question. Nitrogen pentoxide decomposes according to equation :
2N₂O_5(g) → 4NO_2(g) + O_2(g)
This first order reaction was allowed to proceed at 40° C and the data below were collected

(i) Calculate the rate constant. Include units with answer.
(ii) What will be the concentration of N₂O₅ after 100 minutes?
(iii) Calculate the initial rate of reaction.
Answer. i) When t = 20 min, [R] = 0.289 mol L^–1
[R]₀ = 0.400 mol L^–1
For a first order reaction,

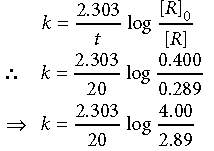
Question. The reaction,

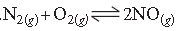
contributes to air pollution whenever a fuel is burnt in air at a high temperature. At 1500 K, equilibrium constant K for it is 1.0 × 10^–5. Suppose in a case [N₂] = 0.80 mol L^–1 and [O₂] = 0.20 mol L^–1 before any reaction occurs. Calculate the equilibrium concentrations of the reactants and the product after the mixture has been heated to 1500 K.
Answer. Given reaction is

or, 4x² = 1.0 × 10–5 × 0.16 or 4x² = 16 × 10^–7
or, x² = 4 × 10^–7 or x = 6.32 × 10^–4
∴ [N₂] = 0.80 – 0.000632 = 0.7994 mol L^–1
[O₂] = 0.20 – 0.000632 = 0.199 mol L^–1
[NO] = 2x = 2 × 0.000632 = 0.001264 mol L^–1