Continuity and Differentiability Class 12 Mathematics Important Questions

Please refer to Continuity and Differentiability Class 12 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.

Class 12 Mathematics Important Questions Continuity and Differentiability

Very Short Answer Type Questions

Question. If x = 2 cos θ – cos 2θ and y = 2sin θ – sin 2θ,then prove that

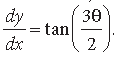
Answer. Here, x = 2 cos θ – cos²θ, y = 2 sin θ – sin²θ

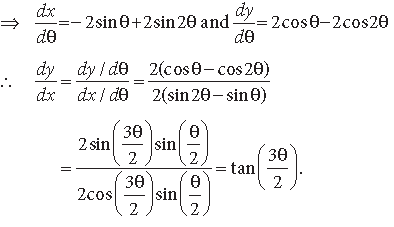
Question. Find the value of ‘a’ if the function f(x) defined by

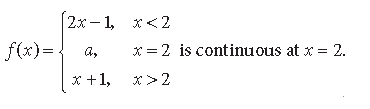
Answer. For f to be continuous at x = 2, we must have

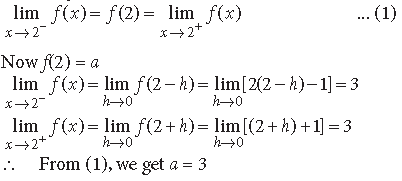
Question. Find all points of discontinuity of f, where f is defined as follows :

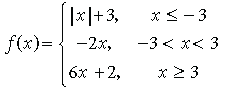
Answer. Continuity at x = – 3 :

Question. For what value of k is the function defined by

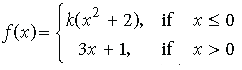
continuous at x = 0 ? Also, write whether the function is continuous at x = 1.
Answer.

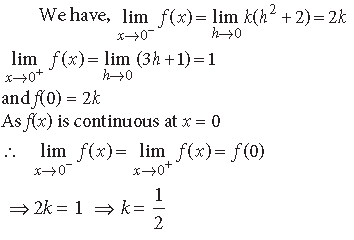
∴ f(x) is continuous at x = 0, if k = 1/2.
Also, f(x) is continuous at x = 1 as f(x) = 3x + 1 is a polynomial function

Question. Find the values of a and b such that the function defined as follows is continuous :

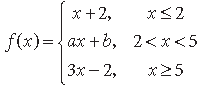
Answer. ∵ f(x) is continuous at x = 2 and x = 5

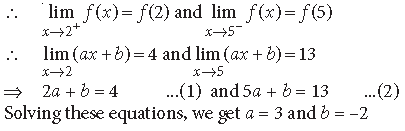
Question. Find dy/dx if x = a (θ + sinθ, y = a (1 – cosθ)
Answer. Given that x = a (θ + sinθ, y = a (1 – cosθ)

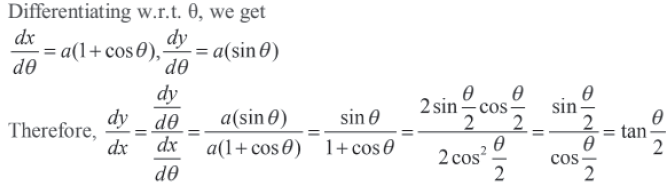
Question. Find the value of k so that the following function is continuous at x = π/2:

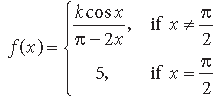
Answer. ∵ f(x) is continuous at x = π/2,

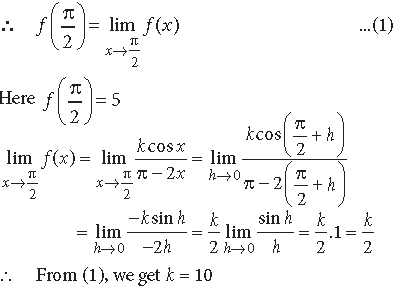
Question. If the function f(x) given by

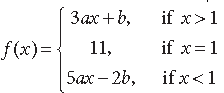
is continuous at x = 1, find the values of a and b.
Answer. ∵ f(x) is continuous at x = 1

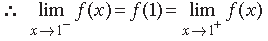
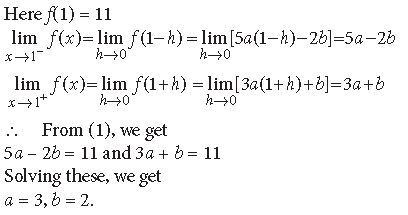
Short Answer Type Questions

Question. Find all points of discontinuity of the function ƒ, where ƒ is defined by

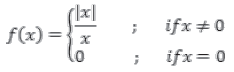
Answer.

Question. Prove that the function ƒ given by ƒ (x) = |x – 1|, for all x∈R Is not differentiable at .
Answer.

Question.

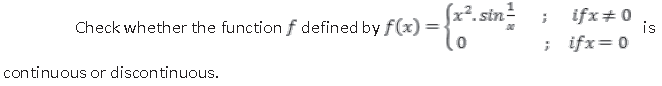
Answer.

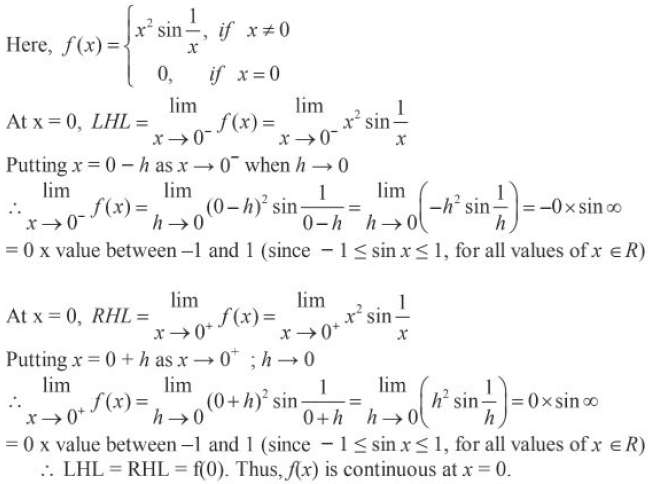
Question. Find the values of k so that the function ƒ, defined by

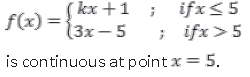
Answer.

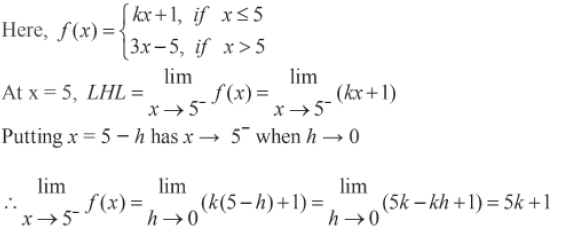
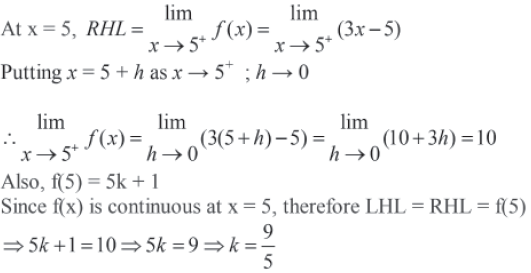
Question.

Answer.

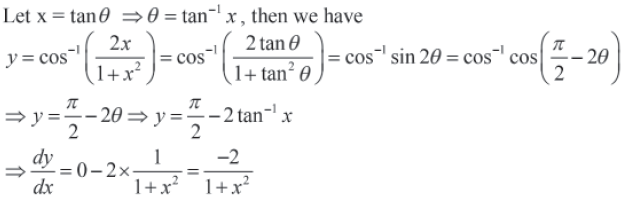
Question.

Answer.

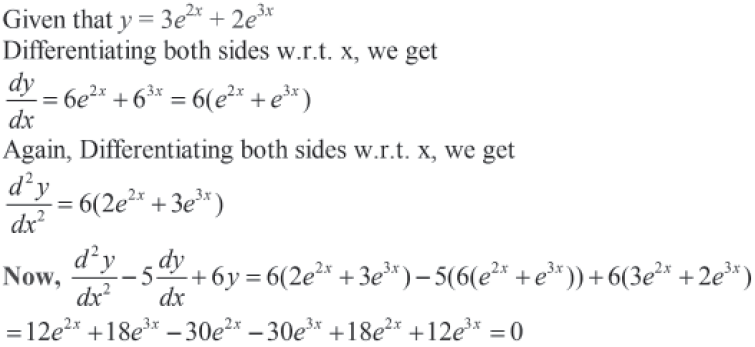
Question. Differentiate sin (tan^-1 e^-x) with respect to
Answer. Let y = sin (tan^-1 e^-x)
Differentiating both sides w.r.t.x, we get

Question. Differentiate the function f (x) = (sin x)^x + sin √x With respect to x.
Answer.

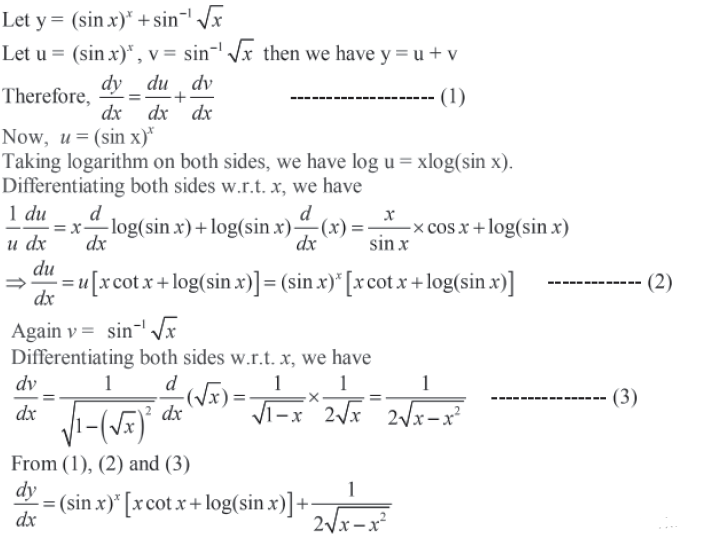
Question. If x = ae^t(sin t + cos t) and y = ae^t(sin t – cos t),

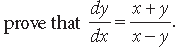
Answer. We have x = ae^t(sin t + cos t)

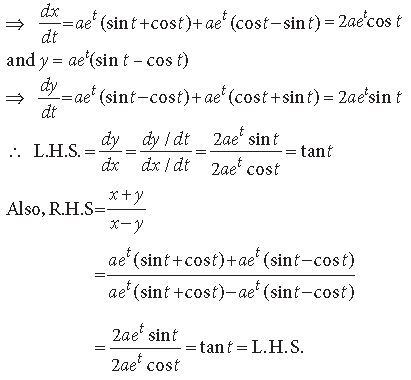
Question.

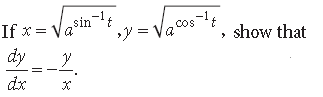
Answer.

Question. If x = a(θ – sin θ) and y = a (1 + cos θ), find dy/dx at θ = π/3
Answer.

Question.

Answer. We have, y = (cosx)^x + (sinx)^1/x

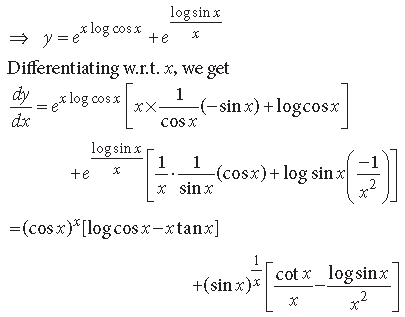
Question. If y = (sin x – cos x)^{sin x – cos x,}

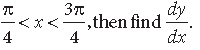
Answer. We have, y = (sin x – cos x)^{(sin x – cos x)}
Taking log on both sides, we get
log y = (sin x – cos x) log (sin x – cos x)
Differentiating w.r.t. x, we get

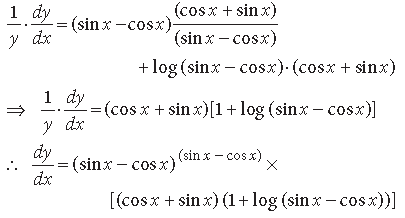
Question. Differentiate the following with respect to x.
(x)^{cos x} + (sin x)^{tan x}
Answer. Let y = (x)^{cos x} + (sin x)^{tan x}
⇒ y = e^{cos x log x} + e^{tan x log sin x}
Differentiating w.r.t. x, we get

Question. If y = (log x)^x + (x)^{cos x}, find dy/dx.
Answer. We have, y = (logx)^x + (x)^cosx
⇒ y = e^xlog(logx) + ec^{osx ·logx}
Differentiating w.r.t. x, we get

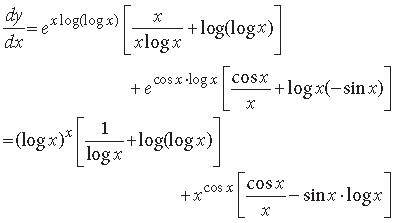
Question. If y = x^x – (sin x)^x, find dy/dx.
Answer. We have, y = x^x – (sinx)^x
⇒ y = e^xlogx – e^{xlog sinx}
Differentiating w.r.t. x, we get

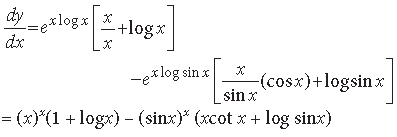
Question.

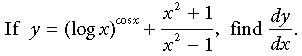
Answer.

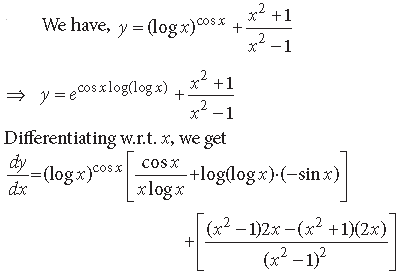
Question. Differentiate (sin x)^{tan x} + (cos x)^{sec x} w.r.t. x.
Answer. Let y = (sin x)^{tan x} + (cos x)^{sec x}
⇒ y = e^{tan x · log sin x} + e^{sec x · log cos x}
Differentiating w.r.t. x, we get

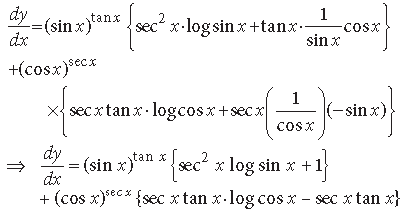
Question. If x = a sin 2t(1 + cos 2t) and
y = b cos 2t(1 – cos 2t), find the values of

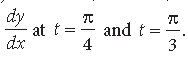
Answer. x = a sin2t (1 + cos2t), y = b cos2t (1 – cos2t)

Question. If x = a (cos t + log tan t/2) and y = a sin t, find dy/dx
Answer. Here, x = a (cos t + log tan t/2)

Question.

Answer. We have, y = x^x
⇒ y = e^{x log x}
Differentiating w.r.t. x, we get

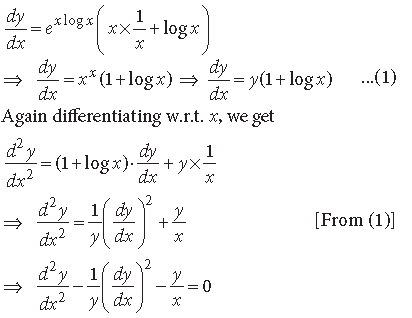
Question. If x = a cos θ + b sin θ, y = a sin θ – b cosθ, show that

Answer. Given, x = a cosθ + b sinθ, y = a sinθ – b cosθ
⇒ x² = a² cos²θ + b² sin²θ + 2ab cosθ sinθ
and y² = a² sin²θ + b² cos²θ – 2ab sinθ cosθ
Adding (1) and (2), we get
x² + y² = a² + b²
Differentiating w.r.t x, we get

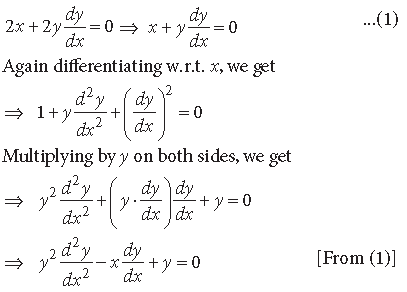
Question.

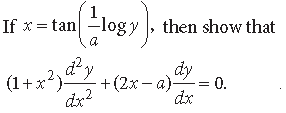
Answer.

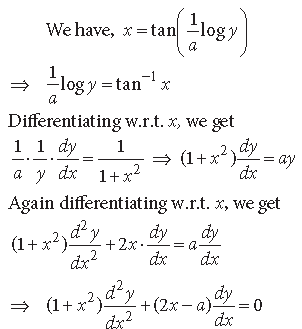
Question. If x = cosθ and y = sin³θ, then prove that

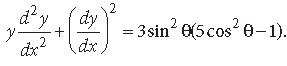
Answer. Given x = cosθ and y = sin³θ

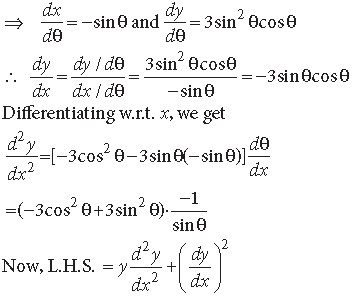
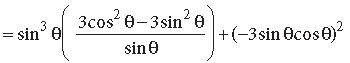
= sin²θ(3cos²θ –3sin²θ) + 9sin²θ cos²θ
= 3 sin²θ(cos²θ – sin²θ + 3cos²θ)
= 3 sin²θ(4cos²θ – sin²θ)
= 3 sin²θ(4cos²θ – 1 + cos²θ)
= 3 sin²θ(5cos²θ –1) = R.H.S.

Question. If y = sin^–1 x, show that

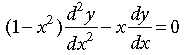
Answer. Given y = sin^–1 x
Differentiating w.r.t. x, we get

Question. If y = (tan^–1x)², show that

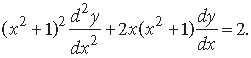
Answer. y = (tan^–1x)²
Differentiating w.r.t. x, we get

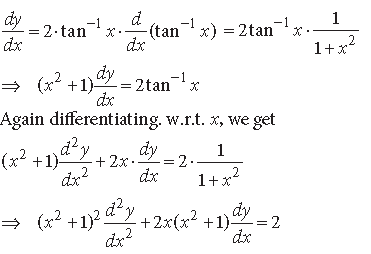
Question. If y = cosec^–1x, x > 1, then show that

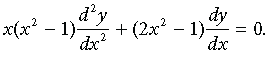
Answer. We have, y = cosec^–1 x

Question. If y = (cot^–1 x)², then show that

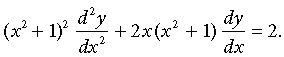
Answer. We have, y = (cot–1x)²

Question.

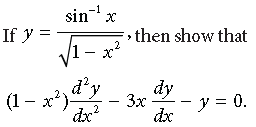
Answer.

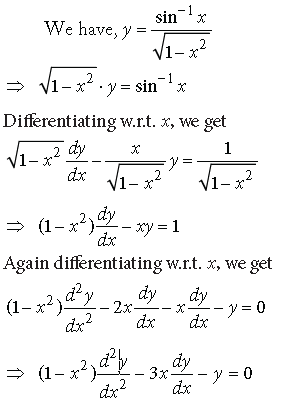
Question. If y = e^x (sin x + cos x), then prove that

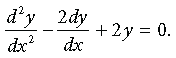
Answer. y = e^x (sin x + cos x)

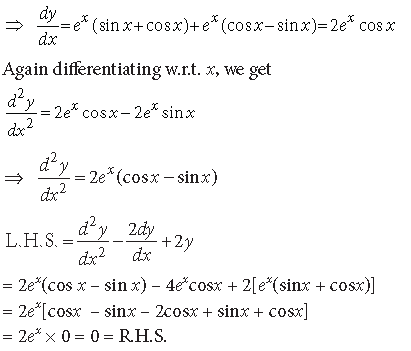
Question. If y = e^x sin x, then prove that

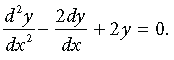
Answer. We have, y = e^x sin x

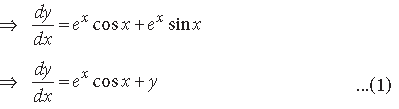
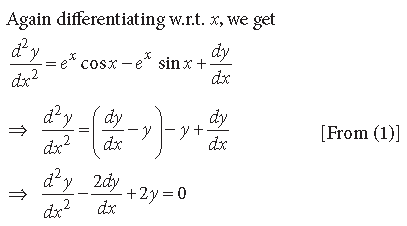
Question. If y = sin(log x), then prove that

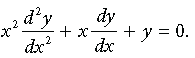
Answer. We have, y = sin (log x)
Differentiating w.r.t. x, we get

Question. If y = e^{m sin-1} x, – 1 ≤ x ≤ 1, then show that 

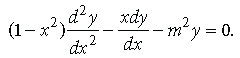
Answer. We have, y = e^{m sin−1 x}
Differentiating w.r.t. x, we get

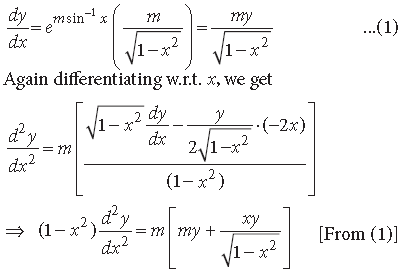
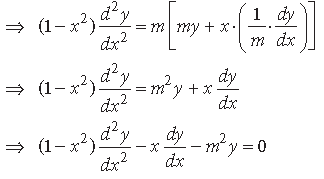
Question.

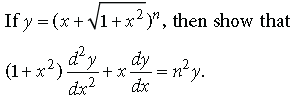
Answer.

Question.

Answer. Here x = a sec³θ

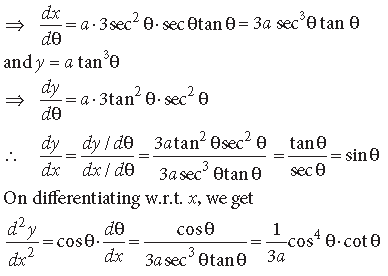
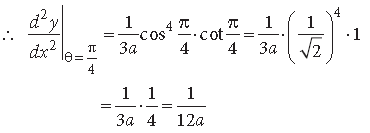
Question. If y = Ae^mx + Be^nx, show that

Answer. Given y = Ae^mx + Be^nx
Differentiating w.r.t. x, we get

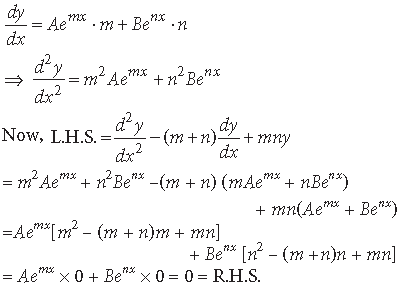
Question. If x = a(cos t + t sin t) and y = a(sin t – t cos t), then find the value of

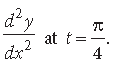
Answer. Here, x = a(cos t + t sin t)

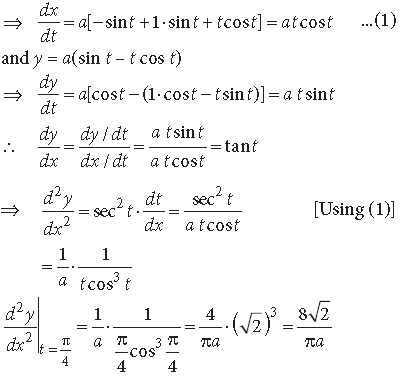
Question. Find dy/dx if y_x + x^y + x^x = a^b
Answer. y_x + x^y + x^x = a^b

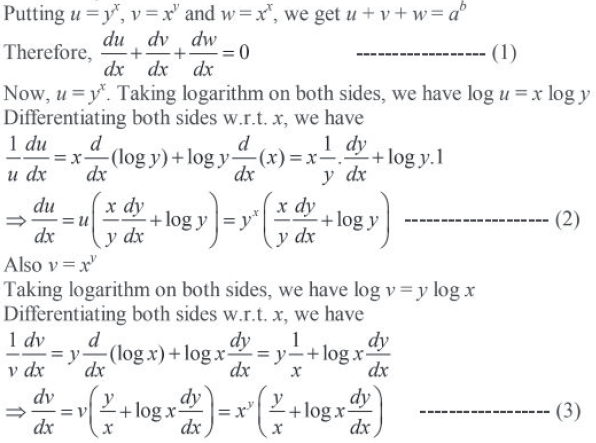
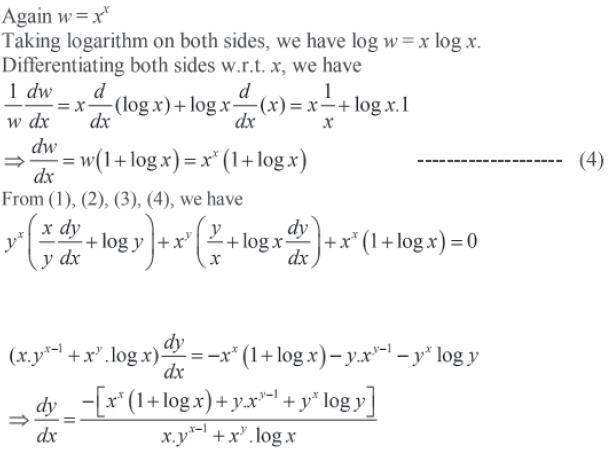
Question. if y = xx – 2^sinx, find dy/dx
Answer. y = xx – 2^sinx

Question. if y = (tan^-1 x)², then show that (x² + 1)²y₂ + 2x(x² + 1)y¹ = 2
Answer. Given that y = (tan^-1 x)²

Question. Differentiate sin² x with respect to e^cosx
Answer.

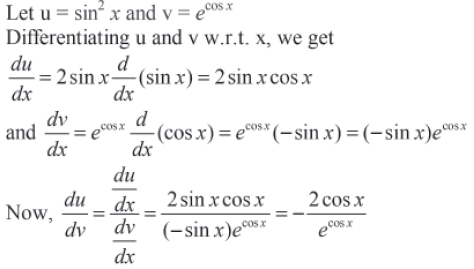
Question.

Answer.

Question.

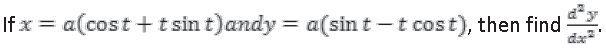
Answer.

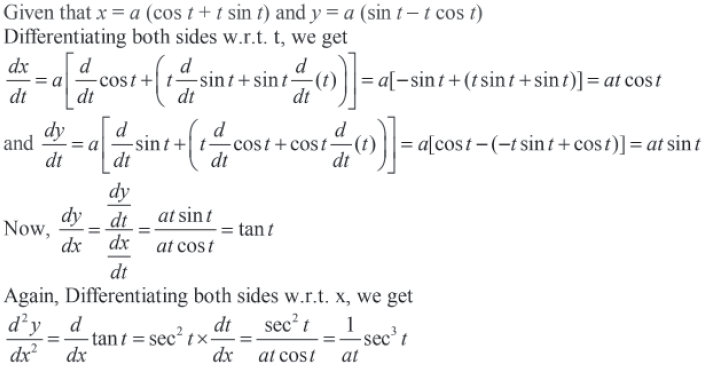
Question. if y = 3 cos (log x + 4 sin (log x), then show that x²y2 + xy₁ + y = 0
Answer.

Long Answer Type Questions

Question.

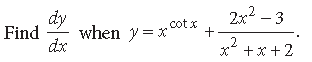
Answer.

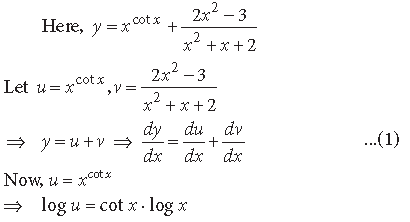
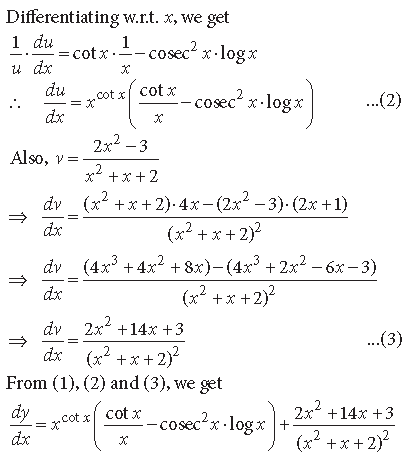
Question.

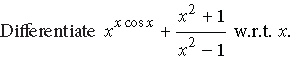
Answer.

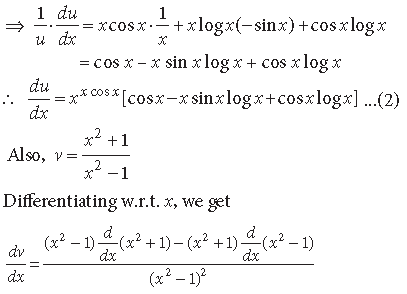
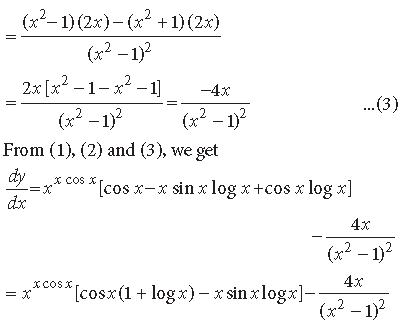
Question. Differentiate

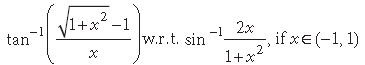
Answer.

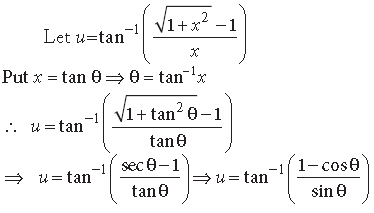
CASE STUDY:

The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x -1/2 x² where x is the number of days exposed to sunlight.

Question. The rate of growth of the plant with respect to sunlight is ______ .
a. 4x-1/2 x²
b. 4 – x
c. x – 4
d. x – 12 x²

Question. What is the number of days it will take for the plant to grow to the maximum height?
a. 4
b. 6
c. 7
d. 10

Question. What is the maximum height of the plant?
a. 12 cm
b. 10 cm
c. 8 cm
d. 6 cm

Question. What will be the height of the plant after 2 days?
a. 4cm
b. 6 cm
c. 8cm
d. 10cm

Question. If the height of the plant is 7/2 cm, the number of days it has been exposed to the sunlight is ______ .
a. 2
b. 3
c. 4
d. 1

CASE STUDY :

The shape of a toy is given as f(x) = 6(2x⁴ – x²). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2,3), above the toy.

Question. Which value from the following may be abscissa of critical point?
a. ±14
b. ±12
c. ± 1
d. None

Question. Find the slope of the normal based on the position of the stick.
a. 360
b. –360
c. 1/360
d. −1/360

Question. What will be the equation of the tangent at the critical point if it passes through (2,3)?
a. x + 360y = 1082
b. y = 360x – 717
c. x = 717y + 360
d. none

Question. Find the second order derivative of the function at x = 5.
a. 598
b. 1176
c. 3588
d. 3312

Question. At which of the following intervals will f(x) be increasing?
a. (-∞, -1/2) ꓴ (1/2, ∞)
b. (-1/2, 0) ꓴ (1/2, ∞)
c. (0, ½) ꓴ (1/2, ∞)
d. (-∞, -1/2) ꓴ (0, ½)