Please refer to Assignments Class 9 Mathematics Polynomials Chapter 2 with solved questions and answers. We have provided Class 9 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 2 Polynomials Class 9 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Polynomials Assignments Class 9 Mathematics
Solved Examples
Easy
Example 1: Which of the following expressions are polynomials? Justify your answers.
i) 2×1/2 + 3x + 4
ii) 8×3 + 7 + x
iii) 2×3 – √2y5
iv)√121x – 2/3 y2 + x3
v) 5(√x)2 + 9×2
vi) 14/x2 – 9×2
Solution:
i) 2×1/2 + 3x + 4
This expression is not a polynomial because the exponent of the first term is 1/2 , which is not a whole number.
ii) 8×3 + 7 + x
This expression is a polynomial as all the coefficients are real numbers and the exponents of the variable x are whole numbers.
ii) 2×3 – √2y5
This expression is a polynomial as all the coefficients are real numbers and the exponents of the variables x and y are whole numbers.
iv) √121x – 2/3 y2 + x3 = 11x – 2/3 y2+x3
This expression is a polynomial as all the coefficients are real numbers and the exponents of the variables x and y are whole numbers.
v) 5(√x)2 + 9×2
This expression is a polynomial because it can be written as 5x + 9×2, in which all the coefficients are real numbers and the exponents of the variable x are whole numbers.
vi) 14/x2 – 9×2
This expression is not a polynomial because it can be written as14x−2 − 9×2, in which the variable in the first term has a negative exponent.
Example 2: For each of the given polynomials, state whether it is a monomial, binomial or trinomial.
i) 4×3
ii) 13y5 − y
iii) 29t3 + 14t − 9
iv) x − x2
Solution:
i) 4×3 is a monomial as it has only one term.
ii) 13y5 − y is a binomial as it has two terms.
iii) 29t3 + 14t − 9 is a trinomial as it has three terms.
iv) x − x2 is a binomial as it has two terms.
Example 1: For each of the given polynomials, state whether it is a monomial, binomial or trinomial.
i) (4×3 + 3y) − (3×3 + x2) + (y − x3)
ii) (t2 + 1)2
iii) [(m − 1) (m + 1)] + 2m2 + 1
Solution:
i) (4×3 + 3y) − (3×3 + x2) + (y − x3)
= 4×3 + 3y − 3×3 − x2 + y − x3
= (4×3 − 3×3 − x3) − x2 + (3y + y)
= − x2 + 4y
The polynomial can be reduced to −x2 + 4y, which has two terms; so, it is a binomial.
ii) (t2 + 1)2
= (t2)2 + 2t2 + 12[∵ (a + b)2 = a2 + 2ab + b2]
= t4 + 2t2 + 1[∵ (am)n = am × n]
The polynomial can be reduced to t4 + 2 t2 + 1, which has three terms; so, it is a trinomial.
iii) [(m − 1) (m + 1)] + 2m2 + 1
= (m2 − 1) + 2m2 + 1 [∵ (a − b) (a + b) = a2 − b2]
= m2 + 2m2 − 1 + 1
= 3m2
The polynomial can be reduced to 3m2, which has only one term; so, it is a monomial.
Example 1: State whether or not the following expressions are polynomials. Justify your answers.

Solution:

In the reduced form of the given expression, all the coefficients are real numbers and the exponents of the variables x and y are whole numbers. Hence, the given expression is a polynomial.
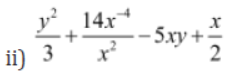
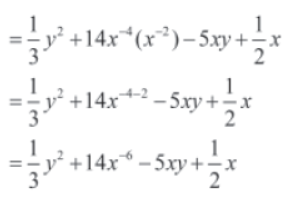
In the reduced form of the given expression, the exponent of the second term (i.e., −6) is not a whole number. Hence, the given expression is not a polynomial.
Example 1: Find the coefficient of x in the following polynomials.
i) π/2 x3 – 3×2
ii)(2×2 − x) + 7 + 3x
Solution:
i) π/2 x3 – 3×2
This expression can also be written as π/2 x3 – 3×2 + 0.x
Thus, in the given polynomial, the coefficient of x is 0.
ii)(2×2 − x) + 7 + 3x
= 2×2 − x + 7 + 3x
= 2×2 + 2x + 7
Thus, in the given polynomial, the coefficient of x is 2.
Example 1: For each of the following polynomials, write the constant term and the coefficient of the variable having the highest exponent.
i) -(x4)1/2 – 3(√x3)2 + (x + 2) − 4
ii)3 (y + 2)2 − 5y (y2 + 2/y) + y3
Solution:
i) -(x4)1/2 – 3(√x3)2 + (x + 2) − 4
= -x41/2 − 3×3 + (x + 2) − 4 [∵ (am)n = am × n and (√a)2 = a ]
= −x2 − 3×3 + x − 2
= − 3×3 − x2 + x − 2
In this reduced form of the given polynomial, we have:
Constant term = −2
Term with the highest exponent = −3×3
So, coefficient of the variable having the highest exponent = −3
ii)3 (y + 2)2 − 5y (y2 + 2/y)+y3
= 3 (y2+ 4y + 4) − 5y3 − 10 + y3
= 3y2+ 12y + 12 − 4y3 − 10
= −4y3 + 3y2+ 12y + 2
In this reduced form of the given polynomial, we have:
Constant term = 2
Term with the highest exponent = −4y3
So, coefficient of the variable having the highest exponent = −4
Example 1: Find the coefficients of x3, x2, x, y3, y2 and y in the following polynomials. Also, find the real constants.
i)17×4 − 3y − x (2×3 + x) + 3 (2y − 4×2 + 1) − 4
ii) y4(3/2y -2)-1/2(6×2 + y+1)+y-4×2
Solution:
i)17×4 − 3y − x (2×3 + x) + 3 (2y − 4×2 + 1) − 4
= 17×4 − 3y − 2×4 − x2 + 6y − 12×2 + 3 − 4
= 15×4 − 13×2 + 3y − 1
This reduced form of the given polynomial can be further written as:
15×4 + 0.×3 − 13×2 + 0.x + 0.y3 + 0.y2 + 3y − 1
Therefore, we have:
Coefficient of x3 = 0 Coefficient of x2 = −13 Coefficient of x = 0
Coefficient of y3 = 0 Coefficient of y2 = 0 Coefficient of y = 3
Real constant = −1
ii) y4(3/2y -2)-1/2(6×2 + y+1)+y-4×2
= 3/2y x y4 – 2y4 – 1/2 x 6×2 – 1/2 x y- 1/2 + y-4×2
= 3/2,y3 – 2y4 – 3×2 -1/2 y+y-4×2-1/2
= 3/2y3 – 2y4 – 7×2 + 1/2y-1/2
= -7×2 – 2y4 + 3/2y3 + 1/2y – 1/2
This reduced form of the given polynomial can be further written as:
0.×3 – 7×2 + 0.x – 2y4 + 3/2y3 + 0.y2 + 1/2y – 1/2
Therefore, we have:
Coefficient of x3 = 0 Coefficient of x2 = −7 Coefficient of x = 0
Coefficient of y3 = 3/2 Coefficient of y2 = 0 Coefficient of y = 1/2
Real constant = -1/2
Example 1: Express the given polynomials in the standard form.
(i) −2y3 + 5y5 − 2 + y
(ii) 11a − a6 − 2a3 + a2 − 1
Solution:
We know that if the terms of a polynomial are written in descending order or ascending order of the powers of the variables then the polynomial is said to be in the standard form.
♦ Given polynomials can be written in the standard form as follows:
(i) Given form: −2y3 + 5y5 − 2 + y
♦ Standard form: 5y5 − 2y3 + y − 2 or −2 + y − 2y3 + 5y5
(ii) Given form: 11a − a6 − 2a3 + a2 − 1
♦ Standard form: −a6 − 2a3 + a2 + 11a − 1 or −1 + 11a + a2 − 2a3 − a6
Example 2: Express the given polynomials in the index form and coefficient form.
♦ (i) 2m7 + 12m5− 7m2 − m
♦ (ii) −4p6 + 3p3− 2p + 7
Solution:
♦ We know that the polynomial obtained on adding the missing terms is said to be in the index form.
♦ Also, when the coefficients of all the terms of a polynomial are written in a bracket by separating with comma then the polynomial is said to be written in the coefficient form.
♦ Given polynomials can be written in the index form and coefficient form as follows:
(i) Given form: 2m7 + 12m5− 7m2 − m
♦ Index form: 2m7 + 0m6 + 12m5 + 0m4 + 0m3 − 7m2 − m
♦ Coefficient form: (2, 0, 12, 0, 0, −7, −1)
(ii) Given form: −4p6 + 3p3− 2p + 7
♦ Index form: −4p6 + 0p5+ 0p4 + 3p3 + 0p2 −2p + 7
♦ Coefficient form: (−4, 0, 0, 3, 0, −2, 7)
♦ Example 3: Express the given coefficient forms in the index forms by taking x as the variable.
♦ (i) (10, 0, −2, 1, 0, 0, 7)
♦ (ii) (−1, 2, 0, 3, 0, 6)
Solution:
Given polynomials can be written in the index form as follows:
(i) Given form: (10, 0, −2, 1, 0, 0, 7)
Index form: 10×6 + 0x5 − 2×4 + x3 + 0x2 + 0x + 7
(ii) Given form: (−1, 2, 0, 3, 0, 6)
Index form: −x5 + 2×4 + 0x3 + 3×2 + 0x + 6
Example 1: Find the degree of each term of the polynomial 3×6 + 3×4 − 6x + 3. Also find the degree of the polynomial.
Solution:
The degree of the term 3×6 is 6.
The degree of the term 3×4 is 4.
The degree of the term −6x is 1.
The degree of the term 3 is 0.
Here, the highest degree is 6. Hence, the degree of the polynomial is 6.
Example 1: Write the degree of each of the following polynomials.
i) x2/2x – 9×7 + 1/x-4 + 7
ii) x2/3 + 4x-1/x-2 – 5×2+x/2 – 9
Solution:

In the given polynomial, the highest degree is 7. Hence, the degree of the polynomial is 7.

In the given polynomial, the highest degree is 2. Hence, the degree of the polynomial is 2.
Example 1: Write the degree of each of the following polynomials.
(i) 24a2b – abc + 11abc2 + ab2c3 – 7a2b2
(ii) 5p5 + 10p2qr – 9p2qr2 – p2r2 + 2pq2 – 2p3q2r
Solution:
(i) Let us find the sum of the powers of all variables in each term of 24a2b – abc + 11abc2 + ab2c3 – 7a2b2.
Sum of the powers of all variables in the term 24a2b = 2 + 1 = 3
Sum of the powers of all variables in the term –abc = 1 + 1 + 1 = 3
Sum of the powers of all variables in the term 11abc2 = 1 + 1 + 2 = 4
Sum of the powers of all variables in the term ab2c3= 1 + 2 + 3 = 6
Sum of the powers of all variables in the term –7a2b2 = 2 + 2 = 4
Among all the sums, 6 is the highest and thus, the degree of the polynomial 24a2b – abc +
11abc2 + ab2c3 – 7a2b2 is 6.
(ii) Let us find the sum of the powers of all variables in each term of 5p5 + 10p2qr –
9p2qr2 – p2r2 + 2pq2 – 2p3q2r.
Sum of the powers of all variables in the term 5p5 = 5
Sum of the powers of all variables in the term 10p2qr = 2 + 1 + 1 = 4
Sum of the powers of all variables in the term –9p2qr2 = 2 + 1 + 2 = 5
Sum of the powers of all variables in the term –p2r2 = 2 + 2 = 4
Sum of the powers of all variables in the term 2pq2 = 1 + 2 = 3
Sum of the powers of all variables in the term –2p3q2r = 3 + 2 + 1 = 6
Among all the sums, 6 is the highest and thus, the degree of the polynomial 5p5 + 10p2qr – 9p2qr2 – p2r2 + 2pq2 – 2p3q2r is 6.
Example 1: Classify each of the given polynomials according to its degree.
i) 11×3 + 7x + 3
ii) 8×2 + 3x
iii) x + 5
iv) 9t3
Solution:
i) 11×3 + 7x + 3
The degree of this polynomial is 3. Hence, it is a cubic polynomial.
ii) 8×2 + 3x
The degree of this polynomial is 2. Hence, it is a quadratic polynomial.
iii) x + 5
The degree of this polynomial is 1. Hence, it is a linear polynomial.
iv) 9t3
The degree of this polynomial is 3. Hence, it is a cubic polynomial.
Example 2: Give an example of each of the following polynomials.
i) A monomial of degree 50
ii) A binomial of degree 17
iii) A trinomial of degree 99
Solution:
i) A monomial of degree 50 means a polynomial having one term and 50 as the highest exponent. An example of such a polynomial is 23y50.
ii) A binomial of degree 17 means a polynomial having two terms and 17 as the highest exponent. An example of such a polynomial is 41t17 + 53t.
iii) A trinomial of degree 99 means a polynomial having three terms and 99 as the highest exponent. An example of such a polynomial is p99 + 5p − 12.
Example 1: Classify each of the given polynomials according to its degree.
i) x2/3 + 4×3 -(5×2 + 4×3) + x/2 -9
ii) x + 3×2 + (x + 2) (x2 + 4 − 2x) + 54
Solution:
i) x2/3 + 4×3 -(5×2 + 4×3) + x/2 -9
= x2/3 + 4×3 -5×2 + 4×3 + x/2 -9
= x2/3 – 5×2 + x/2 – 9
= -14×2/3 + x/2 – 9
The degree of this polynomial is 2. Hence, it is a quadratic polynomial.
ii) x + 3×2 + (x + 2) (x2 + 4 − 2x) + 54
= x + 3×2 + (x3 + 23) + 54 [∵ a3 + b3 = (a + b) (a2 + b2 − ab)]
= x + 3×2 + x3 + 8 + 54
= x + 3×2 + x3 + 62
The degree of this polynomial is 3. Hence, it is a cubic polynomial.
Example 1: Find the value of the polynomial x2 + 5x + 9 at x = −2.
Solution:
Let p(x) = x2 + 5x + 9
On replacing x with −2, we get:
p(−2) = (−2)2 + 5(−2) + 9
= 4 − 10 + 9
= 3
Thus, at x = −2, the value of x2 + 5x +9 is 3.
Example 2: If p(x)= x2-x/4 , then find the value of p(3).
Solution:
It is given that p(x)= x2-x/4
On replacing x with 3, we get:
p(x) = (3)2 – 3/4
= 9 – 3/4
= 33/4
Thus, the value of x2 – x/4 at p(3) is 33/4 .
Example 1: If p(x) = x (x − 4) and q(y) = (y +5) (y + 9), then show that p(24) = q(15).
Solution:
We have p(x) = x (x − 4)
∴ p(24) = 24 (24 − 4)
= 480 … (1)
Also, q(y) = (y +5) (y + 9)
∴ q(15) = (15 + 5) (15 + 9)
= 20 × 24
= 480 … (2)
From equations 1 and 2, we get:
p(24) = q(15)
Example 2: If p(a) = (3a − 2) (3a + 2) and q(b) = b (b + 5)2, then find the value of q(25) − p(18).
Solution:
We have p(a) = (3a − 2) (3a + 2)
⇒ p(a) = (3a)2 − 22 [∵ (a − b) (a + b) = a2 − b2]
∴ p(18) = (3 × 18)2 − 22
= 542 − 22
= 2916 − 4
= 2912
Also, q(b) = b(b +5)2
∴ q(25) = 25 (25 +5)2
= 25 × 302
= 25 × 900
= 22500
Now, q(25) − p(18) = 22500 − 2912 = 19588
Example 1: If p(x) = x3 − 5ax2 + 3bx and p(2) = p(5), then prove that 35a − 3b = 39.
Solution:
We have p(x) = x3 − 5ax2 + 3bx
∴ p(2) = 23 − 5 × a × 22 + 3 × b × 2
= 8 − 20a + 6b … (1)
And p(5) = 53 − 5 × a × 52 + 3 × b × 5
= 125 − 125a + 15b … (2)
According to the given information:
p(2) = p(5)
So, on using equations 1 and 2, we get:
8 − 20a + 6b = 125 − 125a + 15b
⇒ 125a − 20a + 6b − 15b = 125 − 8
⇒ 105a − 9b = 117
⇒ 3 (35a − 3b) = 117
⇒ ∴ 35a − 3b = 39
Example 1: Check if 5/2 is a zero of the polynomial, p(x) = 2×2 + 3x − 20.
Solution:
We have the polynomial, p(x) = 2×2 + 3x − 20.
On replacing x with 5/2 , we get:
p(5/2) = 2(5/2)2 + 3(5/2) – 20
= 25/2 + 15/2 – 20
= 20-20
= 0
So, the value of p(x) is zero at x = 5/2 Hence, 5/2 is a zero of the polynomial.
Example 2: Check if −k is a zero of the polynomial, p(t) = 2t3 − 2t (1 − t) + 3k.
Solution:
We have the polynomial, p(t) = 2t3 − 2t (1 − t) + 3k.
On replacing t with −k, we get:
p(−k) = 2 (−k)3 − 2 (−k) [1 − (−k)] + 3k
= −2k3 + 2k (1 + k) + 3k
= −2k3 + 2k + 2k2 + 3k
= −2k3 + 2k2 + 2k + 3k
= −2k3 + 2k2 + 5k
Clearly, the value of p(t) is not zero at t = −k. Hence, −k is not a zero of the polynomial.
Example 1: Find the value of a for which 3 is the zero of the polynomial, g(z) = 5z2 − 7z + 6a.
Solution:
We have the polynomial, g(z) = 5z2 − 7z + 6a.
It is given that 3 is a zero of g(z). This means that g(3) = 0
⇒ 5 × 32 − 7 × 3 + 6a = 0
⇒ 45 − 21 + 6a = 0
⇒ 24 + 6a = 0
⇒ 6a = −24
⇒ a = −4
Thus, 3 is a zero of the polynomial 5z2 − 7z + 6a when a = −4.
Example 2: Find the zeroes of the following polynomials.
i) p(x) = 4x − 5
ii) p(x) = x2 − 2x
iii) p(x) = 3x + 4
Solution:
i) We have the polynomial, p(x) = 4x − 5.
To find the zero, let us put p(x) = 0.
⇒ 4x − 5 = 0
⇒ 4x = 5
⇒ x = 5/4
Therefore, 5/4 is the zero of the polynomial 4x − 5.
ii) We have the polynomial, p(x) = x2 − 2x
To find the zero, let us put p(x) = 0.
⇒ x2 − 2x = 0
⇒ x (x − 2) = 0
⇒ We can have x = 0 or x − 2 = 0.
⇒ x = 0 or x = 2
Therefore, 0 and 2 are the two zeroes of the polynomial x2 − 2x.
iii) We have the polynomial, p(x) = 3x + 4.
To find the zero, let us put p(x) = 0.
⇒ 3x + 4 = 0
⇒ 3x = −4
⇒ x = -4/3
Therefore, -4/3 is the zero of the polynomial 3x + 4.
Example 1: Find the zero of the polynomial, p(y) = a (y − a) − b (y − b), where a − b ≠ 0.
Solution:
We have the polynomial, p(y) = a (y − a) − b (y − b).
To find the zero, let us put p(y) = 0.
⇒ a (y − a) − b (y − b) = 0
⇒ ay − a2 − by + b2 = 0
⇒ ay − by = a2 − b2
⇒ y (a − b) = (a − b) (a + b)
⇒ y = a + b
Hence, a + b is the zero of the polynomial a (y − a) − b (y − b).
Example 2: A stone is thrown upward from the ground. After gaining a height of 12 m, the change in height of the stone is given by the relation 10t − 5t2, where t represents time in seconds. Calculate the time taken by the stone to return to the ground.
Solution:
The change in the height of the stone is given by the polynomial, p(t) = 10t − 5t2.
The height of the stone becomes zero when it reaches the ground.
Therefore, we have p(t) = 0.
⇒ 10t − 5t2 = 0
⇒ 5t (2 − t) = 0
⇒ We can have t = 0 or 2 − t = 0.
⇒ t = 0 or t = 2
Time, t = 0 when the stone reaches the maximum height of 12 m. So, the time taken by the stone to reach the ground is two seconds.
Example 1: Divide the polynomial by monomial and write the quotient and remainder.
(i) 9y3 – 6y2 + 3y ÷ 3y
(ii) 8×4 + 4×2 – 5x + 1 ÷ 2x
(iii) 4z6 – 18z4 + 24z2 ÷ 12z
Solution:
(i) 9y3 – 6y2 + 3y can be divided by 3y using long division method as follows:

Therefore,
Quotient = 3y2 – 2y + 1
Remainder = 0
(ii) 8×4 + 4×2 – 5x + 1 can be divided by 2x using long division method as follows:
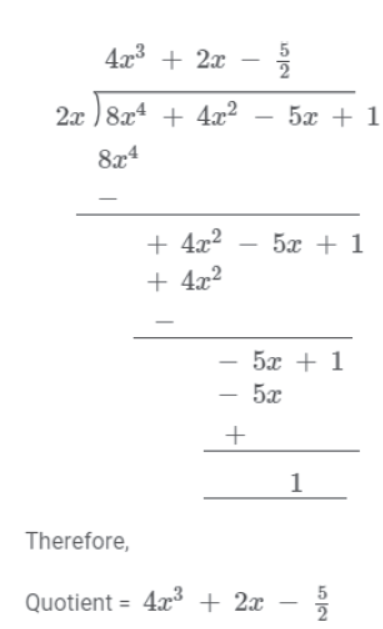
Remainder = 1
(iii) 4z6 – 18z4 + 24z2 can be divided by 12z using long division method as follows:

Therefore,
Quotient = 1/3z5 – 3/2z3 + 2z
Remainder = 0
Example 2: Divide 5×2 + 7x − 4 by x + 1.
Solution:
Let p(x) = 5×2 + 7x − 4 and q(x) = x + 1
The terms of p(x) and q(x) are arranged in decreasing order of their powers. Let us divide p(x) by q(x).
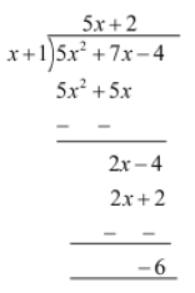
Example 3: What is the quotient when −2×2 + x3− 9x + 18 is divided by x − 2?
Solution:
Let p(x) = −2×2 + x3− 9x + 18
= x3 − 2×2 − 9x + 18 (arranging the terms in decreasing order of their powers)
Let q(x) = x − 2
The terms of p(x) and q(x) are arranged in decreasing order of their powers. Let us divide p(x) by q(x).
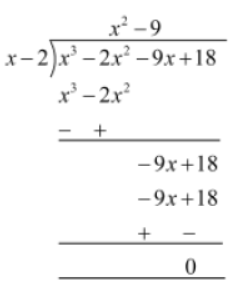
Hence, when −2×2 + x3− 9x + 18 is divided by x − 2, the quotient is x2 − 9.
Example 1: Find the quotient and remainder on dividing f(x) by g(x), where
f(x) = 6×3 + 13×2 + x − 2 and g(x) = 2x + 1.
Solution:
We have f(x) = 6×3 + 13×2 + x − 2 and g(x) = 2x + 1.
The terms of f(x) and g(x) are arranged in decreasing order of their powers. Let us divide f(x) by g(x).

Thus, when 6×3 + 13×2 + x − 2 is divided by 2x + 1, we get 3×2 + 5x − 2 as the quotient and zero as the remainder.
Example 2: What are the quotient and remainder when x4 + 2×3 − 33×2 + 18x + 28 is divided by x + 7?
Solution:
Let p(x) = x4 + 2×3 − 33×2 + 18x + 28 and q(x) = x +https://www.google.co.in/?gws_rd=ssl 7
The terms of p(x) and q(x) are arranged in decreasing order of their powers. Let us divide p(x) by q(x).

Thus, when x4 + 2×3 − 33×2 + 18x + 28 is divided by x + 7, we get x3 − 5×2 + 2x + 4 as the quotient and zero as the remainder.
Example 1: If the division of x3 + 2×2 + kx + 3 by x − 3 yields 21 as the remainder, then find the quotient and the value of k.
Solution:
Let p(x) = x3 + 2×2 + kx + 3 and q(x) = x − 3. It is given that the division of p(x) by q(x) gives
21 as the remainder.
According to the division algorithm:
Dividend = Divisor × Quotient + Remainder
⇒ x3 + 2×2 + kx + 3 = (x − 3) × Quotient + 21
⇒ x3 + 2×2 + kx + 3 − 21 = (x − 3) × Quotient

Now, 3k + 27 = 0
⇒ 3k = −27
⇒ k = −9
So, quotient = x2 + 5x + (k + 15)
= x2 + 5x + (−9 + 15)
= x2 + 5x + 6
Example 2: Divide 3×3 + 5×2 + 4x + 7 by 3x − 1. Find the quotient and the remainder, and verify using the division algorithm.
Solution:
Let p(x) = 3×3 + 5×2 + 4x + 7 and q(x) = 3x − 1
The terms of p(x) and q(x) are arranged in decreasing order of their powers. Let us divide p(x) by q(x).
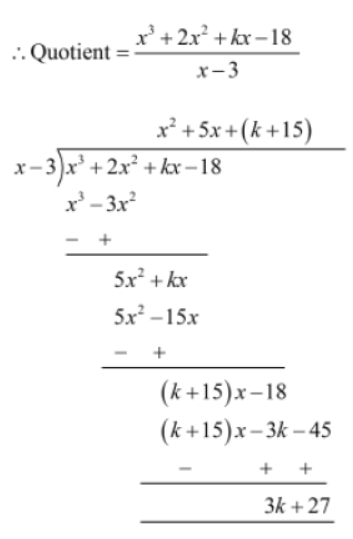
We have obtained the quotient as x2 + 2x + 2 and the remainder as 9.
Let us verify our result using the division algorithm, which states that:
Dividend = Divisor × Quotient + Remainder
Now,
Divisor × Quotient + Remainder = [(3x − 1) (x2 + 2x + 2)] + 9
= [3x (x2 + 2x + 2) − 1 (x2 + 2x + 2)] + 9
= 3×3 + 6×2 + 6x − x2 − 2x − 2 + 9
= 3×3 + 5×2 + 4x + 7
= Dividend
Thus, the division satisfies the division algorithm.
Example 1: Find the remainder when x3 − x2a + 5xa is divided by x − a.
Solution: Let p(x) = x3 − x2a + 5xa
According to the remainder theorem, if p(x) is divided by x − a, then the remainder will
be p(a).
On putting x − a = 0, we get x = a.
∴ Remainder = p(a)
= a3 − a2 × a + 5 × a × a
= a3 − a3 + 5a2
= 5a2
Thus, when x3 − x2a + 5xa is divided by x − a, we get 5a2 as the remainder.
Example 2: What is the remainder when 81×4 + 54×3− 9×2− 3x + 2 is divided by 3x + 2?
Solution:
Let p(x) = 81×4 + 54×3 − 9×2 −3x + 2
As per the remainder theorem, if p(x) is divided by ax + b, then the remainder will be p(-b/a)
On putting 3x + 2 = 0, we get x = -2/3
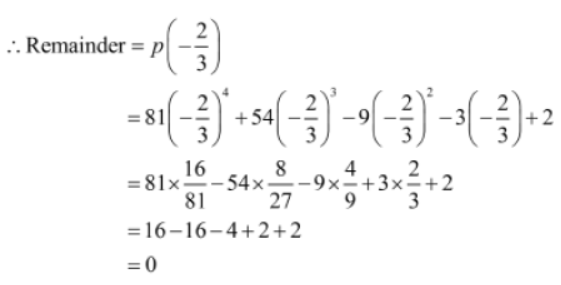
Thus, when 81×4 + 54×3 − 9×2 − 3x + 2 is divided by 3x + 2, we get zero as the remainder.
Example 1: Verify the remainder theorem for the division of 2×3 − 3×2 + 4 by x − 3.
Solution:
Let p(x) = 2×3 − 3×2 + 4
Let us divide p(x) by x − 3 using the long division method.

Thus, the division of 2×3 − 3×2 + 4 by x − 3 yields the remainder 31.
Let us now find the remainder using the remainder theorem. According to this theorem, if p(x) is divided by x − a, then the remainder will be p(a).
On putting x − 3 = 0, we get x = 3.
∴ Remainder = p(3)
= 2 × 33 − 3 × 32 + 4
= 54 − 27 + 4
= 31
Clearly, the remainder obtained by using the remainder theorem is the same as that obtained via the long division method. Hence, the remainder theorem is verified.
Example 2: For what value of m is p(x) = mx3 + 17×2− 31x− 2m completely divisible by 3x + 1.
Solution:
It is given that p(x) = mx 3 + 17x 2 − 31x − 2m
If p(x) is completely divisible by ax + b, then the remainder will be zero, i.e., p(-b/a) = 0
On putting 3x + 1 = 0, we get x = -1/3
Using the remainder theorem, we can find the value of m as follows:
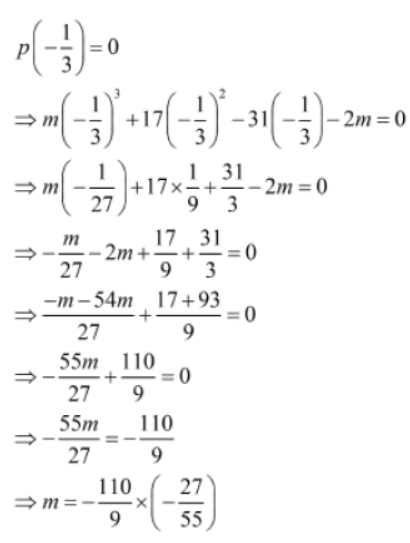
⇒ m = 6
Thus, when m = 6, mx3 + 17×2 − 31x − 2m is completely divisible by 3x + 1.
Example 1:
Find the value of k for which p(x) = 4kx3 − 13x − 3k + 2
i) is exactly divisible by 2x − 1.
ii) leaves 3 as the remainder when divided by 2x + 3.
Solution:
i)We have p(x) = 4kx3 − 13x − 3k + 2
As per the remainder theorem, if p(x) is divided by ax − b, then the remainder will be p(b/a) .
On putting 2x − 1 = 0, we get x = 1/2 .
Now, if 4kx3 − 13x − 3k + 2 is exactly divisible by 2x − 1, then the remainder will be zero, i.e.,p(1/2) = 0
Using the remainder theorem, we can find the value of k as follows:

Thus, when k = -9/5 , 4kx3 − 13x − 3k + 2 is exactly divisible by 2x − 1.
ii)As per the remainder theorem, if p(x) is divided by ax + b, then the remainder will be p(-b/a)
On putting 2x + 3 = 0, we get x = -3/2 .
It is given that the division of 4kx3 − 13x − 3k + 2 by 2x + 3 yields the remainder 3, i.e., p(-3/2) = 3
Using the remainder theorem, we can find the value of k as follows:

Thus, when k = 37/33 , the division of 4kx3 − 13x − 3k + 2 by 2x + 3 leaves 3 as the remainder.
Example 2: Find the values of a and b for which p(x) = x3 + ax2 + bx − 20 leaves 0 and −2 as the remainders when divided by x − 5 and x − 3 respectively.
Solution:
We have p(x) = x3 + ax2 + bx − 20
As per the remainder theorem, if p(x) is divided by x − a, then the remainder will be p(a).
On putting x − 5 = 0, we get x = 5.
On putting x − 3 = 0, we get x = 3.
Now, if the division of x3 + ax2 + bx − 20 by x − 5 leaves 0 as the remainder, then p(5) = 0.
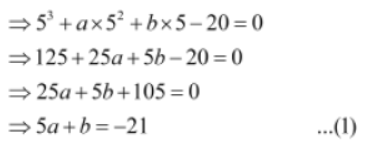
Also, if the division of x3 + ax2 + bx − 20 by x − 3 leaves −2 as the remainder, then p(3) = −2.

On solving equations 1 and 2, we get:
5a + (−3 − 3a) = −21 (∵ b = −3 − 3a)
⇒ 5a − 3a − 3 = −21
⇒ 2a = −21 + 3
⇒ 2a = −18
⇒ a = −9
Now, b = −3 − 3a
⇒ b = − 3 − 3 × (−9)
⇒ b = − 3 + 27
⇒ b = 24
Example 1: Check whether or not x − 1 is a factor of x3 − 2×2 − x + 2.
Solution:
Let p(x) = x3 − 2×2 − x + 2
According to the factor theorem,x − 1 will be a factor of p(x) if p(1) = 0.
p(1)= 13 − 2 × 12 − 1 + 2
= 1 − 2 − 1 + 2
= 0
Thus, x − 1 is a factor of x3 − 2×2 − x + 2.
Example 2: Using the factor theorem, show that 2x + 1 is a factor of 2×3 + 3×2− 11x− 6.
Solution:
Let p(x) = 2×3 + 3×2 − 11x − 6
According to the factor theorem, 2x + 1 will be a factor of p(x) if p(-1/2) = 0

Thus, 2x + 1 is a factor of 2×3 + 3×2 − 11x − 6.
Example 1: For what value of m is x − 3 a factor of 3×2 − 3x + m?
Solution:
Let p(x) = 3×2 − 3x + m
According to the factor theorem, x − 3 will be a factor of p(x) if p(3) = 0.
p(3) = 3 × 32 − 3 × 3 + m
So, 3 × 32 − 3 × 3 + m = 0
⇒ 3 × 9 − 9 + m = 0
⇒ 27 − 9 + m = 0
⇒ 18 + m = 0
⇒ m = −18
Thus, x − 3 is a factor of 3×2 − 3x + m when m = −18.
Example 2: Check whether or not 2×2 − 11x + 25 is exactly divisible by 2x − 3.
Solution:
Let p(x) = 2×2 − 11x + 25 and q(x) = 2x − 3
We know that p(x) will be exactly divisible by q(x) if q(x) is a factor of p(x).
On putting 2x − 3 = 0, we get x = 3/2 .
On using the factor theorem, we get:
p(3/2) = 2(3/2)2 – 11(3/2)+ 25
= 9/2 – 33/2 + 25
= 13
≠ 0
Thus, q(x) is not a factor of p(x).
Hence, 2×2 − 11x + 25 is not exactly divisible by 2x − 3.
Example 3: Using the factor theorem, determine whether or not g(x) is a factor of f(x), where f(x) = 7×2− 2√8 x− 6 and g(x) = x−√2 .
Solution:
It is given that f(x) = 7×2 − 2√8 x − 6 and g(x) = x − √2 .
According to the factor theorem, g(x) will be a factor of f(x) if f(√2) = 0
f(√2) = 7(√2)2 – 2√8 x √2 – 6
= 7 × 2 − 2 √16 – 6
= 14 − 8 − 6
= 0
Therefore, g(x) is a factor of f(x).
Example 1: Using the factor theorem, show that a−b, b−c and c−a are factors of a (b2 −c2) + b (c2−a2) + c (a2−b2) .
Solution:
We have the given expression as a (b2 − c2) + b (c2 − a2) + c (a2 − b2).
As per the factor theorem, x − k will be a factor of a polynomial p(x) if p(x) = 0 when x = k.
Let us consider p(a) = a (b2 − c2) + b (c2 − a2) + c (a2 − b2) to be a polynomial in variable ‘a’.
Take b and c as constants for the time being.
Now, as per the factor theorem, a − b will be a factor of p(a) if p(a) = 0 when a = b.
On putting a = b in p(a), we get:
b (b2 − c2) + b (c2 − b2) + c (b2 − b2)
= b3 − bc2 + bc2 − b3 + c × 0
= 0
Thus, a − b is a factor of a (b2 − c2) + b (c2 − a2) + c (a2 − b2).
Now, suppose p(b) = a (b2 − c2) + b (c2 − a2) + c (a2 − b2) is a polynomial in variable ‘b’ and a and c are constants. Then, b − c will be a factor of p(b) if p(b) = 0 when b = c.
On substituting b = c in p(b), we find that the result is zero.
Similarly, we can take p(c) = a (b2 − c2) + b (c2 − a2) + c (a2 − b2) to be a polynomial in variable ‘c’ and a and b as constants. Then, c − a will be a factor of p(c) if p(c) = 0 when c = a.
On substituting c = a in p(c), we find that the result is zero.
Hence, b − c and c − a are also factors of a (b2 − c2) + b (c2 − a2) + c (a2 − b2).
Example 1: Factorise x2 − 7x + 10 using the factor theorem.
Solution:
Let p(x) = x2 − 7x + 10
The constant term is 10 and its factors are ±1, ±2, ±5 and ±10.
Let us check the value of the polynomial for each of these factors of 10.
p(1) = 12 − 7 × 1 + 10 = 1 − 7 + 10 = 4 ≠ 0
Hence, x − 1 is not a factor of p(x).
p(2) = 22 − 7 × 2 + 10 = 4 − 14 + 10 = 0
Hence, x − 2 is a factor of p(x).
p(5) = 52 − 7 × 5 + 10 = 25 − 35 + 10 = 0
Hence, x − 5 is a factor of p(x).
We know that a quadratic polynomial can have a maximum of two factors. We have obtained the two factors of the given polynomial, which are x − 2 and x − 5.
Thus, we can write the given polynomial as:
p(x) = x2 − 7x + 10 = (x − 2) (x − 5)
Example 1: Factorise x4y2 − 5x2y2 + 6y2.
Solution:
x4y2 − 5x2y2 + 6y2 = y2 (x4 − 5×2 + 6)
Let x2 = a
⇒ (x2)2 = a2
⇒ x4 = a2
∴ x4y2 − 5x2y2 + 6y2 = y2 (a2 − 5a + 6)
= y2 × f(a), where f(a) = a2 − 5a + 6
Here, f(a) is a quadratic polynomial and the factors of the constant term ‘6’ are ±1, ±2, ±3 and ±6.
f(1) = 12 − 5 × 1 + 6 = 1 − 5 + 6 = 2 ≠ 0
Thus, a − 1 is not a factor of f(a).
f(2) = 22 − 5 × 2 + 6 = 4 − 10 + 6 = 0
Thus, a − 2 is a factor of f(a).
f(3) = 32 − 5 × 3 + 6 = 9 − 15 + 6 = 0
Thus, a − 3 is a factor of f(a).
We know that a quadratic polynomial can have a maximum of two factors. We have obtained the two factors of the given polynomial, which are a − 2 and a − 3.
Thus, we can write the given polynomial as:
f(a) = a2 − 5a + 6 = (a − 2) (a − 3)
Hence, x4y2 − 5x2y2 + 6y2 = y2 (a − 2) (a − 3)
= y2 (x2 − 2) (x2 − 3)
Example 2: Factorise 4x (y2 + x − 1 + 3/x) + y2 (y2 − 2) − 20.
Solution:
4x (y2 + x − 1 + 3/x) + y2 (y2 − 2) − 20
= 4xy2 + 4×2 − 4x + 12 + (y2)2 − 2y2 − 20
= (2x)2 + (y2)2 + 2 × 2x × y2 − 4x − 2y2 + 12 − 20
= (2x + y2)2 − 2 (2x + y2) − 8
= a2 − 2a − 8
= f(a), where a = 2x + y2
Here, f(a) is a quadratic polynomial and the factors of the constant term ‘8’ are ±1, ±2, ±4 and ±8.
f(1) = 12 − 2 × 1 − 8 = 1 − 2 − 8 = −9 ≠ 0
Thus, a − 1 is not a factor of f(a).
f(−1) = (−1)2 − 2 × (−1) − 8 = 1 + 2 − 8 = −5 ≠ 0
Thus, a + 1 is not a factor of f(a).
f(2) = 22 − 2 × 2 − 8 = 4 − 4 − 8 = −8 ≠ 0
Thus, a − 2 is not a factor of f(a).
f(−2) = (−2)2 − 2 × (−2) − 8 = 4 + 4 − 8 = 0
Thus, a + 2 is a factor of f(a).
f(4) = 42 − 2 × 4 − 8 = 16 − 8 − 8 = 0
Thus, a − 4 is a factor of f(a).
We know that a quadratic polynomial can have a maximum of two factors. We have obtained the two factors of the given polynomial, which are a + 2 and a − 4.
Thus, we can write the given polynomial as:
f(a) = a2 − 2a − 8 = (a + 2) (a − 4)
Hence, 4x (y2 + x − 1 + 3/x) + y2 (y2 − 2) − 20 = (2x + y2 + 2) (2x + y2 − 4)
Example 1: Factorise 12×2 −√2x − 12 by splitting the middle term.
Solution:
The given polynomial is 12×2 − √2 x − 12.
Here, ac = 12 × (−12) = −144. The middle term is -√2 .
Therefore, we have to split -√2 into two numbers such that their product is −144 and their sum is -√2 .
These numbers are -9√2 and 8√2 (∵ −9√2 + 8√2 = -√2 and -9√2 x 8√2 = – 144).
Thus, we have:
12×2 −√2x − 12 = 12×2 − 9√2x + 8√2 x − 12
= 3√2 x(2√2 x -3) + 4(2√2x – 3)
= (2√2 x-3) (3√2 x +4)
Example 2: Factorise 2×2 − 11x + 15 by splitting the middle term.
Solution:
The given polynomial is 2×2 − 11x + 15.
Here, ac = 2 × 15 = 30. The middle term is −11. Therefore, we have to split −11 into two numbers such that their product is 30 and their sum is −11. These numbers are −5 and −6
[∵ (−5) + (−6) = −11 and (−5) × (−6) = 30].
Thus, we have:
2×2 − 11x + 15 = 2×2 − 5x − 6x + 15
= x (2x − 5) − 3 (2x − 5)
= (2x − 5) (x − 3)
Example 1: Factorise (3y − 1)2 − 6y + 2.
Solution:
(3y − 1)2 − 6y + 2 = 9y2 + 1 − 6y − 6y + 2
= 9y2 − 12y + 3
= 3 (3y2 − 4y + 1)
Here, ac = 1 × 3 = 3. The middle term is −4. Therefore, we have to split −4 into two numbers such that their product is 3 and their sum is −4. These numbers are −1 and −3 [∵ (−3) + (−1) = −4 and (−3) × (−1) = 3].
Thus, we have:
3 (3y2 − 4y + 1) = 3 (3y2 − 3y − y + 1)
= 3 [3y (y − 1) − 1 (y − 1)]
= 3 (y − 1) (3y − 1)
Example 2: Find the dimensions of a rectangle whose area is given by the polynomial 20p2 + 69p + 54.
Solution:
We know that area of a rectangle = Length × Breadth
Area of the rectangle is given by the polynomial 20p2 + 69p + 54. So, its factors will be the required dimensions of the rectangle.
In the given polynomial, ac = 20 × 54 = 1080. The middle term is 69. Therefore, we have to split 69 into two numbers such that their product is 1080 and their sum is 69. These numbers are 45 and 24 (∵ 45 + 24 = 69 and 45 × 24 = 1080).
Thus, we have:
20p2 + 69p + 54 = 20p2 + 45p + 24p + 54
= 5p (4p + 9) + 6 (4p + 9)
= (4p + 9) (5p + 6)
Hence, the dimensions of the rectangle are 5p + 6 and 4p + 9.
Example 1: Factorise 2(3x+4/5x)2 + 19(3x+4/5x+9/19)
Solution:
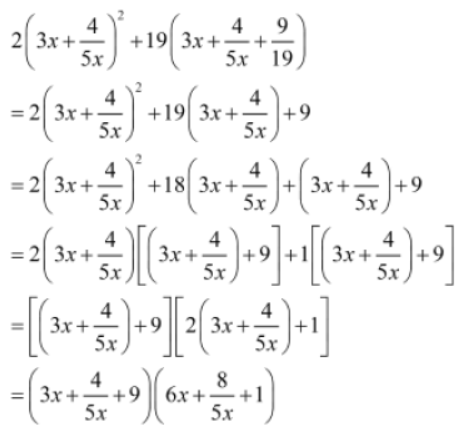
Example 1: Factorize x3 − 3×2 − x + 3.
Solution:
Let p(x) = x3 − 3×2 − x + 3
The constant term is 3.
The factors of 3 are ±1 and ±3.
Let us take x = 1 and find the value of p(x).
p(1) = 13 − 3 × 12 − 1 + 3
= 1 − 3 − 1 + 3
= 0
Thus, x − 1 is a factor of p(x), using factor theorem.
Now, we have to group the terms of p(x) such that we can take x − 1 as common.
Thus, we have:
p(x) = x3 − 3×2 − x + 3
= x3 − x2 − 2×2 + 2x − 3x + 3
= x2 (x − 1) − 2x (x − 1) − 3 (x − 1)
= (x − 1) (x2 − 2x − 3) … (1)
Next, we factorize x2 − 2x − 3 by splitting its middle term.
The middle term is −2. We have to find two numbers such that their product is −3 and their sum is 2. These two numbers are 3 and −1.
Thus, we have:
x2 − 2x − 3 = x2 − (3 − 1)x − 3
= x2 − 3x + x − 3
= x (x − 3) + 1 (x − 3)
= (x − 3) (x + 1)
On substituting in equation 1, we get:
p(x) = (x − 1) (x − 3) ( x + 1)
Example 2: If x + 3 is a factor of the polynomial f(x) = x3 − 7x + 6, then factorize f(x).
Solution:
We have x + 3 as a factor of the polynomial f(x) = x3 + 0x2 − 7x + 6.
Let us divide f(x) by x + 3.
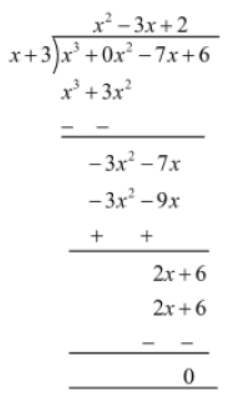
∴ f(x) = x3 − 7x + 6 = (x + 3) (x2 − 3x + 2)
= (x + 3) (x2 − x − 2x + 2)
= (x + 3) [x (x − 1) − 2 (x − 1)]
= (x + 3) (x − 1) (x − 2)
Example 1: Factorize 2×3− 7×2 + 7x − 2.
Solution:
Let p(x) = 2×3 − 7×2 + 7x − 2
Let us take x = 1 and find the value of p(x).
p(1) = 2 × 13 − 7 × 12 + 7 × 1 − 2
= 2 − 7 + 7 − 2
= 0
Thus, x − 1 is a factor of p(x).
Now, we have to group the terms of p(x) such that we can take x − 1 as common.
Thus, we have:
p(x) = 2×3 − 2×2 − 5×2 + 5x + 2x − 2
= 2×2 (x − 1) − 5x (x − 1) + 2 (x − 1)
=(x − 1) (2×2 − 5x + 2) … (1)
Next, we factorize 2×2 − 5x + 2 by splitting its middle term. The middle term is −5. We have to find two numbers such that their product is 4 and their sum is 5. These two numbers are 4 and 1.
Thus, we have:
2×2 − 5x + 2 = 2×2 − (4 + 1)x + 2
= 2×2 − 4x − x + 2
= 2x (x − 2) − 1 (x − 2)
= (2x − 1) (x − 2)
On substituting in equation 1, we get:
p(x) = (x − 1) (2x − 1) (x − 2)
Example 2: Factorize x3 − 23×2 + 142x − 120.
Solution:
Let p(x) = x3 − 23×2 + 142x − 120
Let us take x = 1 and find the value of p(x).
p(1)= 13 − 23 × 12 + 142 × 1 − 120
= 1 − 23 + 142 − 120
= 0
Thus, x − 1 is a factor of p(x).
Now, we have to group the terms of p(x) such that we can take x − 1 as common.
Thus, we have:
p(x)= x3 − 23×2 + 142x − 120
= x3 − x2 − 22×2 + 22x + 120x − 120
= x2 (x −1) − 22x (x − 1) + 120 (x − 1)
= (x − 1) (x 2 − 22x + 120) … (1)
Next, we factorize x2 − 22x + 120 by splitting its middle term. The middle term is −22. We have to find two numbers such that their product is 120 and their sum is 22. These two numbers are 12 and 10.
Thus, we have:
x2 − 22x + 120= x2 − 12x − 10x + 120
= x (x − 12) − 10 (x − 12)
= (x − 12) (x − 10)
On substituting in equation (1), we get:
x3 − 23×2 − 142x − 120 = (x − 1) (x − 12) (x − 10)
Example 1: Factorize the cubic polynomial p(x) = 6×3 + 5×2 − 12x + 4.
Solution:
We have p(x) = 6×3 + 5×2 − 12x + 4
Let us take x = −2 and then find the value of p(x).
p(−2)= 6 × (−2)3 + 5 × (−2)2 − 12 × (−2) + 4
= −48 + 20 + 24 + 4
= 0
Thus, x + 2 is a factor of p(x).
Now, let us divide p(x) by x + 2.
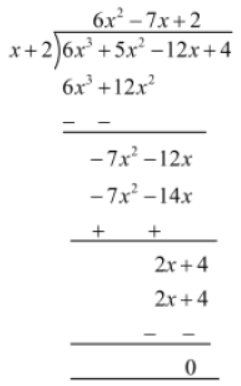
∴ 6×3 + 5×2 − 12x + 4= (x + 2) (6×2 − 7x + 2)
= (x + 2) (6×2 − 4x − 3x + 2)
= (x + 2) [2x (3x − 2) − 1 (3x − 2)]
= (x + 2) (3x − 2) (2x − 1)
Example 1: Expand the following expressions.
i)(ab − bc + ca) 2
ii) (1/2x – 2/3y – 3/4)2
Solution:
i) (ab − bc + ca) 2
On comparing the expression (ab − bc + ca) 2 with (x + y + z) 2, we get:
x = ab, y = −bc and z = ca
On using the identity (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx, we get:
(ab)2 + (−bc)2 + (ca)2 + 2 (ab) (−bc) + 2 (−bc) (ca) + 2 (ca) (ab)
= a2b2 + b2c2 + c2a2 − 2ab2c − 2abc2 + 2a2bc
∴ (ab − bc + ca) 2 = a2b2 + b2c2 + c2a2 − 2ab2c − 2abc2 + 2a2bc
ii) (1/2x – 2/3 y -3/4)2
On comparing the expressi (1/2x – 2/3 y -3/4)2 with (a + b + c) 2, we get:
a = 1/2 x, b =-2/3 y and c = -3/4
On using the identity (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca,we get:

Example 2: Expand the expression (xy + yz + zx)2.
Solution:
On comparing the expression (xy + yz + zx)2 with (a + b + c) 2, we get:
a = xy, b = yz and c = zx
On using the identity (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca,we get:
(xy)2 + (yz)2 + (zx)2 + 2 (xy) (yz) + 2 (yz) (zx) + 2 (zx) (xy)
= x2y2 + y2z2 + z2x2 + 2xy2z + 2xyz2 + 2x2yz
∴ (xy + yz + zx)2 = x2y2 + y2z2 + z2x2 + 2xy2z + 2xyz2 + 2x2yz
Example 1: Factorize the following expressions.
i)8×2 + 12y2 − 8√6 xy + 12 √6x − 36y + 27
ii)8×4 + 4√2 x3 + 25×2 + 6√2 x + 18
Solution:
i)8×2 + 12y2 − 8√6 xy + 12 √6x − 36y + 27
= 8×2 + 12y2 + 27 − 8√6 xy − 36y + 12√6 x
= (2√2x)2 + (−2√3y)2 + (3√3)2 + 2(2√2x)(−2√3y) + 2(−2√3y)(3√3) + 2(3√3)(2√2x)
On using the identity (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca,where a = 2√2x,
b = −2√3 y and c = 3√3 , we are left with (2√2x −2√3y + 3√3)2
∴ 8×2 + 12y2 − 8√6xy + 12√6x − 36y + 27 = (2√2x −2√3y + 3√3)2
ii)8×4 + 4√2×3 + 25×2 + 6√2x + 18
= 8×4 + 25×2 + 18 + 4√2×3 + 6√2x
= 8×4 + x2 + 18 + 4√2×3 + 6√2x + 24×2 (∵ 25×2 = x2 + 24×2)
= (2√2×2)2 + (x)2 + (3√2)2 + 2(2√2×2)(x) + 2(x)(3√2) + 2(3√2)(2√2×2)
On using the identity (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca,where a = 2√2×2,∴ 8×4 + 4√2×3 + 25×2 + 6√2x + 18 = (2√2×2 + x + 3√2)2
Example 2: Find the value of the expression 4×2 + 9y2 + 16z2 − 12xy − 24yz + 16zx for x = 3, y= 4 and z = 5 without substituting the values of the variables in the expression.
Solution:
4×2 + 9y2 + 16z2 − 12xy − 24yz + 16zx
= (2x)2 + (−3y)2 + (4z)2 + 2 (2x) (−3y) + 2 (−3y) (4z) + 2 (4z) (2x)
On using the identity (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca,where a = 2x,
b = −3y and c = 4z, we are left with (2x − 3y + 4z)2
It is given that x = 3, y = 4 and z = 5.
On substituting the values of x, y and z, we get:
(2 × 3 − 3 × 4 + 4 × 5)2
= (6 − 12 + 20)2
= 142
= 196
∴ 4×2 + 9y2 + 16z2 − 12xy − 24yz + 16zx = 196
Example 1: Find the value of ab + bc + ca, where a + b + c = 1 and a2 + b2 + c2 = 29.
Solution:
We know that (a + b + c) 2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
⇒ (a + b + c) 2 = (a2 + b2 + c2) + 2(ab + bc + ca)
⇒ (1)2 = 29 + 2(ab + bc + ca)
⇒ 1 − 29 = 2(ab + bc + ca)
⇒ − 28 = 2(ab + bc + ca)
⇒ ab + bc + ca = -28/2
⇒ ∴ ab + bc + ca = −14
Example 2: If (x + 2)2 + (y − 6)2 + (z − a)2 − 2x (6 + a) + 2y (2 − a) − 8z + 2 (xy + yz + xz) − 8 (3 − a)
= (x + y + z)2, then find the value of a.
Solution:
(x + 2)2 + (y − 6)2 + (z − a)2 − 2x (6 + a) + 2y (2 − a) − 8z + 2 (xy + yz + xz) − 8 (3 − a)
= (x + 2)2 + (y − 6)2 + (z − a)2 − 12x − 2ax + 4y − 2ay − 8z + 2xy + 2yz + 2xz − 24 + 8a
= (x + 2)2 + (y − 6)2 + (z − a)2 − 12x − 2ax + 4y − 2ay − 12z + 4z + 2xy + 2yz + 2xz − 24 + 12a − 4a
= (x + 2)2 + (y − 6)2 + (z − a)2 + 2xy − 12x + 4y − 24 + 2yz − 2ay − 12z + 12a + 2xz − 2ax + 4z − 4a
= (x + 2)2 + (y − 6)2 + (z − a)2 + 2(xy − 6x + 2y − 12) + 2(yz − ay − 6z + 6a) + 2(xz − ax + 2z − 2a)
= (x + 2)2 + (y − 6)2 + (z − a)2 + 2[x(y − 6) + 2(y − 6)] + 2[y(z − a) − 6(z − a)] + 2[x(z − a) + 2(z − a)]
= (x + 2)2 + (y − 6)2 + (z − a)2 + 2 (x + 2) (y − 6) + 2 (y − 6) (z − a) + 2 (x + 2) (z − a)
= [(x +2) + (y − 6) + (z − a)]2
= (x + y + z − 4 − a)2
It is given that
(x + 2)2 + (y − 6)2 + (z − a)2 − 2x (6 + a) + 2y (2 − a) − 8z + 2 (xy + yz + xz) − 8 (3 − a)
= (x + y + z)2
⇒ (x + y + z − 4 − a)2 = (x + y + z)2
⇒ −4 − a = 0
⇒ ∴ a = −4
Example 1: Factorise the following expressions.
i)a3 − 125b3 − 15a2b + 75ab2
ii)27p3 + 125q3
Solution:
i)a3 − 125b3 − 15a2b + 75ab2
= (a)3 − (5b)3 − 15ab (a − 5b)
= (a)3 − (5b)3 − 3 × a × 5b (a − 5b)
On using the identity (x − y)3 = x3 − y3 − 3xy (x − y), where x = a and y = 5b, we are left with
(a − 5b)3
∴ a3 − 125b3 − 15a2b + 75ab2 = (a − 5b)3
ii)27p3 + 125q3
= (3p)3 + (5q)3
On using the identity x3 + y3 = (x + y) (x2 − xy + y2), where x = 3p and y = 5q, we get:
(3p + 5q) [(3p)2 − (3p) (5q) + (5q)2]
= (3p + 5q) (9p2 − 15pq + 25q2)
∴ 27p3 + 125q3 = (3p + 5q) (9p2 − 15pq + 25q2)
Example 2: Evaluate the following expressions using identities.
i)10033
ii)983
Solution:
i)We can write 10033 as:
(1000 + 3)3
On using the identity (x + y)3 = x3 + y3 + 3xy (x + y), where x = 1000 and y = 3, we get:
(1000 + 3)3 = 10003 + 33 + 3 × 1000 × 3 × (1000 + 3)
= 1000000000 + 27 + 9000 × (1000 + 3)
= 1000000000 + 27 + 9000000 + 27000
= 1009027027
ii)We can write 983 as:
(100 − 2)3
On using the identity (x − y)3 = x3 − y3 − 3xy (x − y), where x = 100 and y = 2, we get:
(100 − 2)3 = 1003 − 23 − 3 × 100 × 2 × (100 − 2)
= 1000000 − 8 − 600 × (100 − 2)
= 1000000 − 8 − 60000 + 1200
= 941192
Example 1: Expand the following expressions.
i) (x/a+y/b)3
ii)(2x + 5y)3 − (2x − 5y)3
Solution:
i) (x/a+y/b)3
On using the identity (p + q)3 = p3 + q3 + 3pq (p + q), where p = x/a and q = y/b , we get:

ii) (2x + 5y)3 − (2x − 5y)3
We have two terms in the given expression—(2x + 5y)3 and (2x − 5y)3.
On using the identity (p + q)3 = p3 + q3 + 3pq (p + q), where p = 2x and q = 5y, we get:
(2x + 5y)3 = (2x)3 + (5y)3 + 3 × (2x) (5y) (2x + 5y)
= 8×3 + 125y3 + 30xy (2x + 5y)
= 8×3 + 125y3 + 60x2y + 150xy2
Similarly, on using the identity (p − q)3 = p3 − q3 − 3pq (p − q), we get
(2x − 5y)3 = (2x)3 − (5y)3 − 3 × (2x) (5y) (2x − 5y)
= 8×3 − 125y3 − 30xy (2x − 5y)
= 8×3 − 125y3 − 60x2y + 150xy2
So,
(2x + 5y)3 − (2x − 5y)3 = 8×3 + 125y3 + 60x2y + 150xy2 − [8×3 − 125y3 − 60x2y + 150xy2]
= 8×3 + 125y3 + 60x2y + 150xy2 − 8×3 + 125y3 + 60x2y − 150xy2
= 250y3 + 120x2y
Example 2:The side of a cube is a. If each side of the cube is increased by b/5 , then by how much does its volume increase?
Solution:
Let the side of the cube be a.
Original volume of the cube = a × a × a = a3
After the increase, each side becomes (a+b/5) .
New volume = (a+b/5) (a+b/5) (a+b/5) = (a+b/5)3
On using the identity (x + y)3 = x3 + y3 + 3xy (x + y), where x = a and y = b/5 , we get:
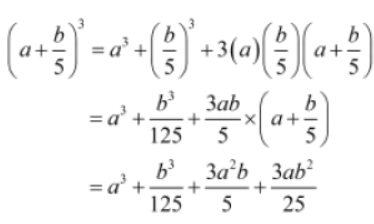
Now,
Increase in volume = New volume − Original volume
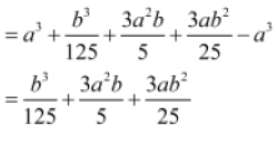
Thus, the volume of the cube increases by b3/125 + 3a2b/5 + 3ab2/25
Example 1: Find the values of the following expressions.
i) x3+1/x3 when x + 1/x = 5
ii) 8y3 – 27/y3 when 4y2 + 9/y2 = 37
iii)125×3 − 27y3 when 5x − 3y = 1 and xy = 6
Solution:
i) x3+1/x3 when x+1/x = 5
We have x+1/x = 5
On cubing both sides, we get:
(x+1/x)3 = 53
On using the identity (a + b)3 = a3 + b3 + 3ab (a + b), where a = x and b = 1/x , we get:
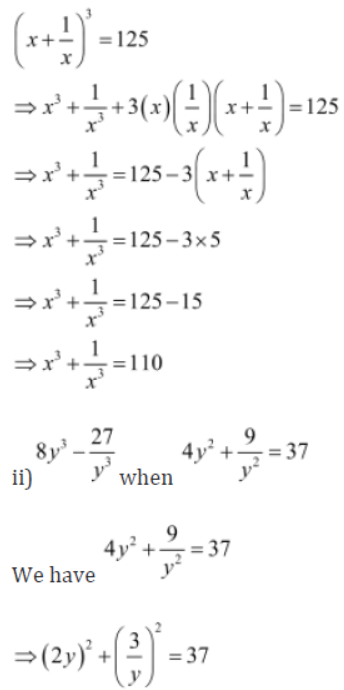
On using the identity a2 + b2 = (a − b)2 + 2ab, where a = 2y and b = 3/y , we get:
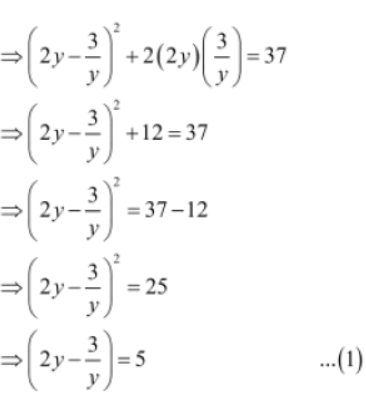
On cubing both sides, we get:
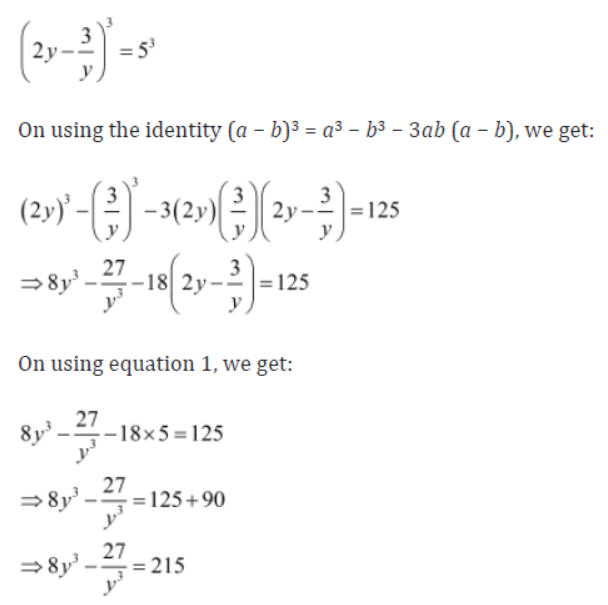
iii)125×3 − 27y3 when 5x − 3y = 1 and xy = 6
We have 5x − 3y = 1
On cubing both sides, we get:
(5x − 3y)3 = 13
On using the identity (a − b)3 = a3 − b3 − 3ab (a − b), where a = 5x and b = 3y, we get:
(5x)3 − (3y)3 − 3 (5x) (3y) (5x − 3y) = 1
⇒ 125×3 − 27y3 − 45xy (5x − 3y) = 1
On substituting the values of xy and (5x − 3y),we get:
125×3 − 27y3 − 45 × 6 × 1 = 1
⇒ 125×3 − 27y3 = 1 + 270
⇒ 125×3 − 27y3 = 271
Example 2: If x + y = 8 and x2 + y2 = 42, then find the value of x3 + y3.
Solution:
It is given that x + y = 8
⇒ (x + y)2 = 82
⇒ x2 + y2 + 2xy = 64
⇒ 42 + 2xy = 64 (∵x2 + y2 = 42)
⇒ 2xy = 64 − 42
⇒ 2xy = 22
⇒ xy = 22/2
⇒ ∴ xy = 11
Now, (x + y)3 = 83
⇒ x3 + y3 + 3xy (x + y) = 512
⇒ x3 + y3 + 3 × 11 × 8 = 512
⇒ x3 + y3 + 264 = 512
⇒ x3 + y3 = 512 − 264
⇒ ∴ x3 + y3 = 248
Example 3: Prove that
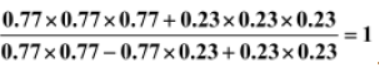
Solution:

Example 1: Factorize the following expressions.
i) 125×3 + 8y3 + 27z3 − 90xyz
ii) 343p3 − 64y3 + 8+ 168py
Solution:
i) 125×3 + 8y3 + 27z3 − 90xyz
= (5x)3 + (2y)3 + (3z)3 − 3 (5x) (2y) (3z)
On using the identity x3 + y3 + z3 − 3xyz = (x + y + z) (x2 + y2 + z2 − xy − yz − zx), we get:
(5x + 2y + 3z) [(5x)2 + (2y)2 + (3z)2 − (5x) (2y) − (2y) (3z) − (3z) (5x)]
= (5x + 2y + 3z) (25×2 + 4y2 + 9z2 − 10xy − 6yz − 15xz)
∴ 125×3 + 8y3 + 27z3 − 90xyz = (5x + 2y + 3z) (25×2 + 4y2 + 9z2 − 10xy − 6yz − 15xz)
ii) 343p3 − 64y3 + 8 + 168py
= (7p)3 + (−4y)3 + (2)3 − 3 (7p) (−4y) (2)
On using the identity x3 + y3 + z3 − 3xyz = (x + y + z) (x2 + y2 + z2 − xy − yz − zx), we get:
[7p + (−4y) + 2] [(7p) 2 + (−4y) 2 + (2) 2 − (7p) (−4y) − (−4y) (2) − (2) (7p)]
= (7p − 4y + 2) (49p2 + 16y2 + 4 + 28py + 8y − 14p)
∴ 343p3 − 64y3 + 8 + 168py = (7p − 4y + 2) (49p2 + 16y2 + 4 + 28py + 8y − 14p)
Example 1: If a + b + c = 10 and ab + bc + ca = 31, then find the value of a3 + b3 + c3 − 3abc.
Solution: We know that a3 + b3 + c3 − 3abc = (a + b + c) (a2 + b2 + c2 − ab − bc − ca)
Or, a3 + b3 + c3 − 3abc = (a + b + c) [a2 + b2 + c2 − (ab + bc + ca)] … (1)
It is given that a + b + c = 10 and ab + bc + ca = 31.
Let us find the value of a2 + b2 + c2.
We have the identity:
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
⇒ (10)2 = a2 + b2 + c2 + 2 × 31
⇒ 100 = a2 + b2 + c2 + 62
⇒ a2 + b2 + c2 = 100 − 62
⇒ a2 + b2 + c2 = 38
On substituting all the values in equation 1, we obtain:
a3 + b3 + c3 − 3abc = 10 × (38 − 31)
⇒ a3 + b3 + c3 − 3abc = 10 × 7
⇒ a3 + b3 + c3 − 3abc = 70
Example 2: Factorise the expression x3/8 – 27/x3 – 11/2
Solution:
We have
x3/8 – 27/x3 – 11/2
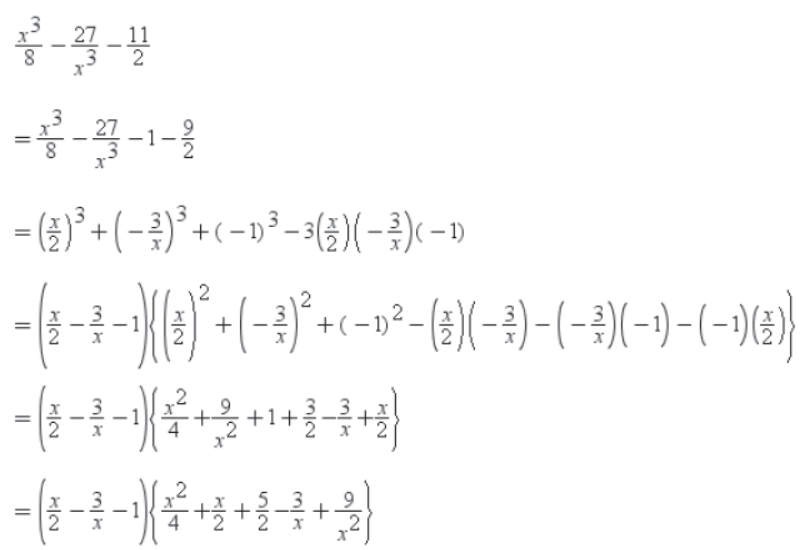
Example 1: Without actually calculating the cubes, find the value of each of the following expressions.
i) (0.2)3 − (0.5)3 + (0.3)3
ii) −123 + 253 − 133
Solution:
i) We can write (0.2)3 − (0.5)3 + (0.3)3 as (0.2)3 + (−0.5)3 + (0.3)3.
Let us consider x = 0.2, y = −0.5 and z = 0.3.
Now, x + y + z = 0.2 − 0.5 + 0.3 = 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz.
On substituting the values of x, y and z, we obtain:
(0.2)3 + (−0.5)3 + (0.3)3 = 3 × 0.2 × (−0.5) × 0.3
⇒ (0.2)3 − (0.5)3 + (0.3)3 = −0.09
ii) We can write −123 + 253 − 133 as (−12)3 + 253 + (−13)3.
Let us consider x = −12, y = 25 and z = −13.
Now, x + y + z = −12 + 25 − 13 = 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz.
On substituting the values of x, y and z, we obtain:
(−12)3 + 253 + (−13)3 = 3 × (−12) × 25 × (−13)
⇒ −123 + 253 − 133 = 11700
Example 1: Find the value of the expression 8×3 + 27y3 − 64z3without directly substituting the values
x = 3, y = 2 and z = 3.
Solution: We can write 8×3 + 27y3 − 64z3 as (2x)3 + (3y)3 + (−4z)3.
For the given values of x, y and z, we get:
(2x) + (3y) + (−4z) = 2 × 3 + 3 × 2 − 4 × 3
⇒ (2x) + (3y) + (−4z) = 6 + 6 − 12
⇒ (2x) + (3y) + (−4z) = 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz.
Thus, we have:
(2x)3 + (3y)3 + (−4z)3 = 3 (2x) (3y) (−4z)
⇒ 8×3 + 27y3 − 64z3 = −72xyz
On substituting the values of x, y and z, we obtain:
8×3 + 27y3 − 64z3 = −72 × 3 × 2 × 3
⇒ 8×3 + 27y3 − 64z3 = −1296
Example 1: Show that
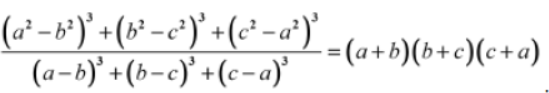
Solution: We will factorize the numerator and the denominator separately.
We have the numerator as (a2 − b2)3 + (b2 − c2)3 + (c2 − a2)3
Let us consider x = a2 − b2, y = b2 − c2 and z = c2 − a2.
Now, x + y + z = a2 − b2 + b2 − c2 + c2 − a2 = 0
We know that if x + y + z = 0, then x3 + y3 + z3 = 3xyz.
Thus, we obtain:
(a2 − b2)3 + (b2 − c2)3 + (c2 − a2)3 = 3 (a2 − b2) (b2 − c2) (c2 − a2)
On using the identity x2 − y2 = (x + y) (x − y), we get:
(a2 − b2)3 + (b2 − c2)3 + (c2 − a2)3 = 3 (a − b) (a + b) (b − c) (b + c) (c − a) (c + a)
We have the denominator as (a − b)3 + (b − c)3 + (c − a)3.
Let us consider x = a − b, y = b − c and z = c − a.
Now, x + y + z = a − b + b − c + c − a = 0
Again, if x + y + z = 0, then x3 + y3 + z3 = 3xyz.
Thus, we obtain:
(a − b)3 + (b − c)3 + (c − a)3 = 3 (a − b) (b − c) (c − a)
On putting back the numerator and the denominator, we get:
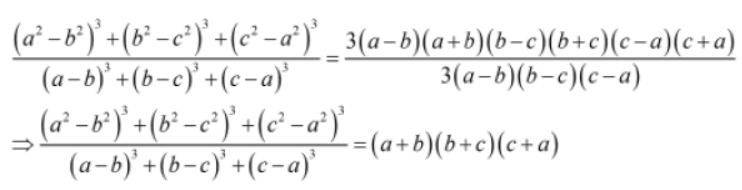
Example : If 2a = 3b = 4c = 24 then without actually calculating the cubes of a, b and c, find the value of 8a3 + 27b3 + 64c3.
Solution: We have,
2a = 3b = 4c = 24
⇒ a = 12, b = 8 and c = 6
Also, 2a + 3b + 4c = 72 ≠ 0
Therefore,
(2a)3 + (3b)3 + (4c)3 − 3(2a)(3b)(4c) = 0
⇒ 8a3 + 27b3 + 64c3 = 72abc
⇒ 8a3 + 27b3 + 64c3 = 72 × 12 × 8 × 6
⇒ 8a3 + 27b3 + 64c3 = 41472


