Please refer to Assignments Class 9 Mathematics Probability Chapter 15 with solved questions and answers. We have provided Class 9 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 15 Probability Class 9 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Probability Assignments Class 9 Mathematics
Solved Examples
Example 1: A fair die is thrown. What is the sample space of this experiment?
Solution: When a die is thrown, we can have six outcomes, namely, 1, 2, 3, 4, 5 and 6.
We know that sample space is the collection of all possible outcomes of an experiment.
∴ Sample space (S) = {1, 2, 3, 4, 5, 6}
Example 2: Which of the following are experiments?
i)Tossing a coin
ii)Rolling a six-sided die
iii)Getting a head on a tossed coin
Solution:
Tossing a coin and rolling a six-sided die are experiments, while getting a head on a tossed coin is the outcome of an experiment.
Example 1: What is the sample space when two coins are tossed together?
Solution:
When two coins are tossed together, we can get four possible outcomes. These are as follows:
i)A head (H) on one coin and a tail (T) on the other
ii)A head (H) on one coin and a head (H) on the other
iii)A tail (T) on one coin and a head (H) on the other
iv)A tail (T) on one coin and a tail (T) on the other
∴ Sample space (S) = {HT, HH, TH, TT}
Easy
Example 1: The given figure shows a wheel with six letters of the English alphabet written in six sectors of equal area.
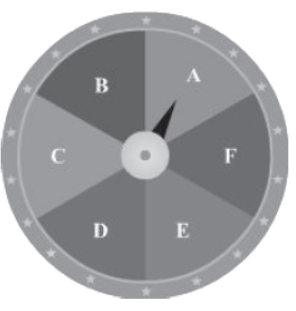
The follwing table shows the results of spinning the wheel ten times.

What is the probability of the most favorable outcome?
Solution:
It can be observed from the table that the most favorable outcome is ‘A’ as it is obtained the most number of times (3) in the experiment.
We know that the experimental probability of an event is given as:

Thus, the probability of the most favourable outcome is 3/10 .
Example 2: In a pack of 5000 bulbs, 250 bulbs are defective. Find the probability that a bulb chosen at random will be non-defective.
Solution:
It is given that:
Total number of bulbs = 5000
Number of defective bulbs = 250
∴ Number of non-defective bulbs = 5000 − 250 = 4750
So, probability of choosing a non-defective bulb = Number of non – defective bulbs/Total number bulbs
= 4750/5000
= 19/20
Medium
Example 1: A die is thrown 100 times. The faces marked with numbers 1, 2, 3, 4, 5 and 6 are observed 20, 15, 25, 10, 10 and 20 times respectively. Find the probability of getting each of these events.
Solution:
Total number of trials = 100
Let E1, E2, E3, E4, E5 and E6 be the respective events of getting the faces marked with
numbers 1, 2, 3, 4, 5 and 6.
Number of outcomes for the face marked ‘1’ = 20
Number of outcomes for the face marked ‘2’ = 15
Number of outcomes for the face marked ‘3’ = 25
Number of outcomes for the face marked ‘4’ = 10
Number of outcomes for the face marked ‘5’ = 10
Number of outcomes for the face marked ‘6’ = 20
We know that:
Probability of an event (E) = Number of outcomes of the event/Number of trials
So, we have:

Example 2: In a survey conducted by a leading newspaper, 1000 families with two children were selected at random and the following data was recorded.

If we choose one of these families at random, then what is the probability that the chosen family has
i)1 boy.
ii)2 boys.
iii)no boy.
Solution:
Let E1, E2 and E3 denote the respective events of a family having one boy, two boys and no boy.
We know that:
Probability of an event (E) = Number of outcomes of the event/Number of trials
Using this formula, we can calculate the probabilities of events E1, E2 and E3.

Hard
Example 1: The monthly salary ranges of 100 workers of a company are given in the following table.

If a worker is chosen at random, then find the probability of selecting a worker
who earns
i)above Rs 3000 per month.
ii)below Rs 2000 per month.
iii)between Rs 24000 and Rs 48000 per annum.
Solution:
i)Total number of workers = 100
Number of workers who earn above Rs 3000 per month = 35 + 15 = 50
Thus, the probability of selecting a worker who earns above Rs 3000 per month is given as:
Number of workers earning above 3000 per month/Total number of workers
= 50/100
= 1/2
ii) Number of workers who earn below Rs 2000 per month = 10 + 15 = 25
Thus, the probability of selecting a worker who earns below Rs 2000 per month is given as:
Number of workers earning below Rs 2000 per month/Total number of workers
= 25/100
= 1/4
iii) Annual salary of the workers = Salaries of 12 months
Now, the monthly salary of workers getting an annual salary of Rs 24000 is given as:
Annual salary/12
= Rs(24000/12)
= Rs 2000
Similarly, the monthly salary of workers getting an annual salary of Rs 48000 is given as:
Annual salary/12
= Rs(48000/12)
= Rs 4000
Number of workers earning between Rs 24000 and Rs 48000 per year
= Number of workers earning between Rs 2000 and Rs 4000 per month
= 25 + 35
= 60
Thus, the probability of selecting a worker who earns between Rs 24000 and Rs 48000 per annum is given as:
Number of workers earning between Rs 2000 and Rs 4000 per month/Total number of workers
= 60/100
= 3/5
Example 2: There are 150 telephone numbers on each page of a telephone directory. The frequency distribution of the unit-place digits in the telephone numbers on a particular page is shown.
Digit:0123456789
Frequency:15221215171216151412
A number is chosen at random. Find the probability that the digit at the unit’s place is
i)6.
ii)a non-zero multiple of 3.
iii)a non-zero even number.
Solution:
i)Total number of telephone numbers = 150
It is given that the digit ‘6’ occurs 16 times at the unit’s place.
∴ Probability that the digit at the unit’s place is 6 = 16/150 = 0.1067
ii)A non-zero multiple of 3 means 3, 6 or 9.
Number of telephone numbers in which the unit’s digit is 3, 6 or 9 = 15 + 16 + 12 = 43
∴ Probability that the digit at the unit’s place is a non-zero multiple of 3 = 43/150 = 0.286
iii)A non-zero even number means 2, 4, 6 or 8.
Number of telephone numbers in which the unit’s digit is 2, 4, 6 or 8 = 12 + 17 + 16 + 14 = 59
∴ Probability that the digit at the unit’s place is a non-zero even number = 59/150 = 0.393


