Ray Optics and Optical Instruments Class 12 Physics Important Questions

Please refer to Ray Optics and Optical Instruments Class 12 Physics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Physics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Physics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.

Class 12 Physics Important Questions Ray Optics and Optical Instruments

Very Short Answer Type Questions

Question. A biconvex lens of focal length f is cut into two identical plano-convex lenses. What will be the focal length of each part?
Answer. The focal length will be 2f.

Question. In viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back ?
Answer. Yes, the angular magnification changes. When the distance between the eye and a magnifying glass is increased, the angular magnification decreases a little. This is because the angle subtended at the eye is slightly less than the angle subtended at the lens. Image distance does not have any effect on angular magnification.

Question. Define the power of a lens. Write its S.I. unit.
Answer. The power of a lens is equal to the reciprocal of its focal length (in metre).
Also accept

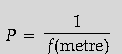
Do not deduct mark if student does not write the word metre.
(Alternatively,
Power of a lens is the ability of convergence/divergence of the rays incident on the lens.)
SI Unit: Dioptre (D)

Question. A double convex lens, lens made of a material of refractive index μ₁ , is placed inside two liquids of refractive indices μ₂ and μ₃ , as shown. μ₂>μ₁>μ₃. A wide, parallel beam of light is incident on the lens from the left. How the rays will be refracted?

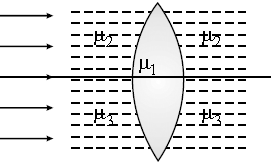
Answer. As μ₂>μ₁, the upper half of the lens will become diverging. As μ₁>μ₃, the lower half of the lens will become converging.

Question. An astronomical telescope consists of an objective and an eyepiece. Whose focal length is greater than the other?
Answer. In astronomical telescope, f₀ > f_e and the magnifying power is equal to f₀ / f_e. This becomes large when f_o > f_e.

Question. If the focal length of objective lens of a microscope and a telescope in increased how the power ?
Answer. Magnifying power of microscope

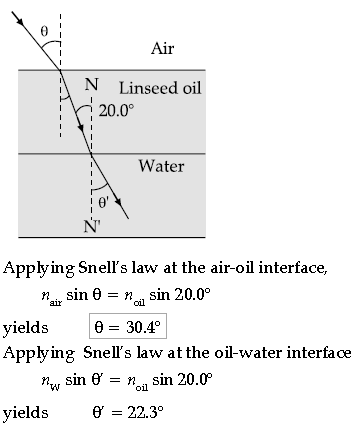
Question. The light beam shown in the figure makes an angle of 20.0° with the normal line NN’ in the linseed oil. Determine the angles θ and θ’. (The index of refraction of linseed oil is 1.48)

Answer

Question. How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced by red light ? Give reason.
Answer. (i) Decreases
(ii) n_Violet > n_Red
Detailed Answer:
We know, δ_m = (n₂₁ – 1)A. Hence, larger the refractive index, larger will be the deviation. As refractive index of glass for violet is more than the refractive index of glass for red, so the deviation will decrease if the incident violet light is replaced by red light.

Question. For a glass prism (μ = √3) the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
Answer. For the condition of minimum deviation, the angle of prism should be equal to the angle of minimum deviation

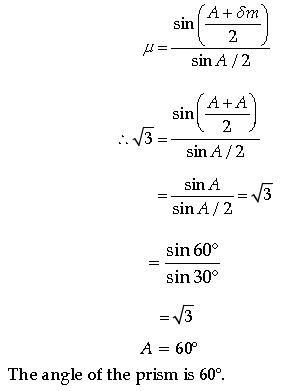
Question. (i) Define refractive index of a medium.
(ii) In the following ray diagram, calculate the speed of light in the liquid of unknown refractive index.

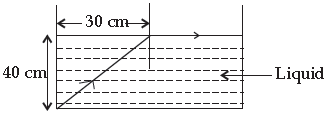
Answer. (i) Refractive index of a medium is the ratio of speed of light (c) in free space to the speed of light (v) in that medium.

Question. An astronomical telescope may be a refracting type or a reflecting type. Which of the two produces image of better quality ? Justify your answer.
Answer. Reflecting type astronomical telescope produces better quality image since due to reflection, there is no loss in intensity of light.

Question. A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece lens of focal length 1.0 cm is used, find the angular magnification of the telescope.
Answer. Given f₀ =15 m, f_e =1.0 cm = 1.0 × 10^-2 m
Angular magnification of telescope,

Question. A microscope is focussed on a mark on a piece of paper and then a slab of glass of thickness 3 cm and refractive index 1.5 is placed over the mark. How should the microscope be moved to get the mark in focus again? 
Answer. Apparent depth = Real depth / μ = 3/1.5 = 2 cm As image appears to be raised by 1 cm, therefore, microscope must be moved upwards by 1 cm.

Question. A beam of light consisting of red, green and blue colours is incident on a right angle prism ABC. The refractive index of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. What will happen?

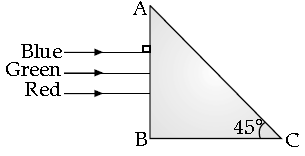
Answer. Red will be refracted. Other two colours will suffer total internal reflection.
[Explanation: As beam of light is incident normally on the face AB of the right angled prism, ABC. So no refraction occurs at face AB and it passes straight and strikes the face AC at an angle of incidence,
i = 45°. For total reflection to take place at face AC,
i > i_c or sini > sin i_c
where i_c is the critical angle.

So, only red colour will be transmitted through face AC, while green and blue colours will suffer total internal reflection.

So the prism will separate red colour from the green and blue colours as shown in the following figure

Question. Define visual angle. Does it vary with distance of the object from the eye ?
Answer. It is the angle subtended by an object or image at the eye. It decreases with increasing distance of the object or image from the eye.

Short Answer Type Questions – I

Question. Calculate the radius of curvature of a equiconcave lens of refractive index 1.5, when it is kept in a medium of refractive index 1.4, to have a power of –5 D ?
Answer. Calculation of focal length Lens maker’s formula Calculation of radius of curvature

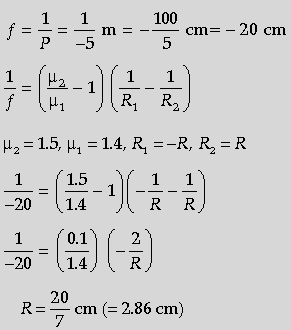
Question. An equilateral glass prism has a refractive index 1.6 in air. Calculate the angle of the minimum deviation of the prism, when kept in a medium of refractive index 4√2/5
Answer. Formula
Substitution and calculation

Question. Draw a labelled ray diagram to show image formation by a compound microscope and write the expression for its resolving power.
Answer. To draw the ray diagram of compound microscope Expression for resolving power
Ray diagram

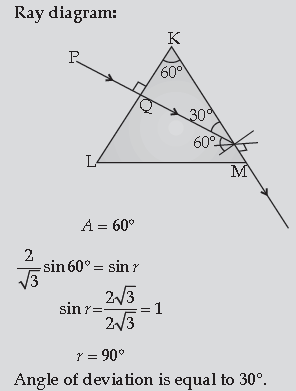
Question. A triangular prism of refracting angle 60° is made of a transparent material of refractive index 2/√3. A ray of light is incident normally on the face KL as shown in the figure. Trace the path of the ray as it passes through the prism and calculate the angle of emergence and angle of deviation.

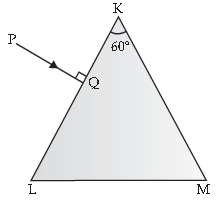
Answer. • Tracing path of ray passing through prism 
• Calculating angle of emergence and angle of deviation 

Question. Why should the objective of a telescope have large focal length and large aperture? Justify your answer.
Answer. Reasons for having large focal length and large aperture of objective of telescope and their justification.
Large focal length: to increase magnifying power

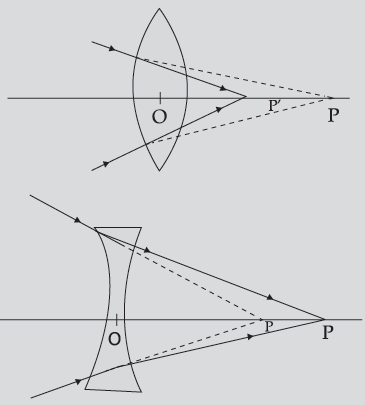
Question. A beam of light converges at a point P. Draw ray diagrams to show where the beam will converge if
(i) a convex lens, and (ii) a concave lens is kept in the path of the beam.
Answer. Ray diagrams to show path of beam of light in case of
(i) Convex lens
(ii) Concave lens

Question. A ray PQ incident normally on the refracting face BA is refracted in the prism BAC made of material of refractive index 1.5. Complete the path of ray through the prism. From which face will the ray emerge ? Justify your answer.

Answer. Path of emergent ray
Naming the face
Justification

Face-AC
Here i_c = sin-1(2/3)
= sin–1(0.6)
∠i on face AC is 30° which is less than ∠i_c. Hence the ray get retracted here.

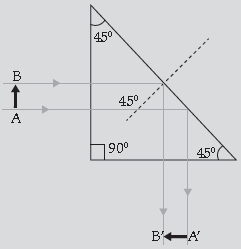
Question. Under what conditions does the phenomenon of total internal reflection take place? Draw a ray diagram showing how a ray of light deviates by 90° after passing through a right-angled isosceles prism. 
Answer. Conditions
Diagram
Conditions:
1. Light travels from denser to rarer medium.
2. Angle of incidence in denser medium must be greater than the critical angle.

Question. Draw the ray diagram of an astronomical telescope showing image formation in the normal adjustment position. Write the expression for its magnifying power.
Answer. To draw the ray diagram of astronomical telescope Expression for magnification

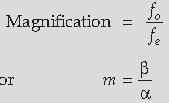
Question. Write two characteristics of image formed when an object is placed between the optical centre and focus of a thin convex lens. Draw the graph showing variation of image distance v with object distance u in this case.
Answer. Two characteristics- virtual and enlarged image and same side of object.

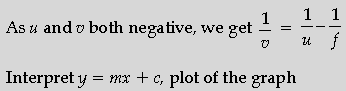
Question. Define the magnifying power of a compound microscope when the final image is formed at infinity. Why must both the objective and the eyepiece of a compound microscope have short focal lengths? Explain.
Answer. Definition of magnifying power
Reason for short focal lengths of objective and eyepiece 
Magnifying power is defined as the angle subtended at the eye by the image to the angle subtended (at the unaided eye) by the object.
(Alternatively: Also accept this definition in the form of formula.)

Short Answer Type Questions – II

Question. A ray of light incident on the face AB of an isosceles triangular prism makes an angle of incidence (i) and deviates by angle b as shown in the figure. Show that in the position of minimum deviation ∠α = ∠β. Also find out the condition when the refracted ray QR suffers total internal reflection.

Answer. Proving α =β
Finding i_c
For minimum deviation,
r₁ + r₂ = A; r₁ = r₂
(90° − β) + (90° − β) = A
180° −2β = A
2β = 180° − A
2β = 2α
β = α
r₁ + r₂ = A
r₁ + i_c = A
i_c = A − r₁
i_c = A − (90° − β)

Question. (i) A giant refracting telescope has an objective lens of focal length 15 m. If an eye piece of focal length 1.0 cm is used, what is the angular magnification of the telescope ?
(ii) If this telescope is used to view the Moon, what is the diameter of the image of the Moon formed by the objective lens ? The diameter of the Moon is 3.48 × 10⁶ m and the radius of lunar orbit is 3.8 × 10⁸ m
Answer. (i) m = − f_o/f_e; ignoring –ve sign as it only shown that image is inverted.
f_o = 1500 cm
f_e = 1 cm

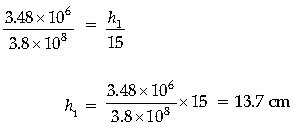
Question. (i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30°. Calculate the speed of light through the prism.

(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
Answer. (i) Calculation of speed of light
(ii) Calculation of angle of incidence at face AB

At face AC, let the angle of incidence be r₂. For grazing ray, e = 90°

Question. (a) Draw a ray diagram showing the formation of image by a reflecting telescope.
(b) Write two advantages of a reflecting telescope over a refracting telescope.
Answer. (a) Ray Diagram for reflecting telescope
(b) Two advantages of it over refracting type of telescope.
(a) Ray Diagram
Arrow marking
Labelling

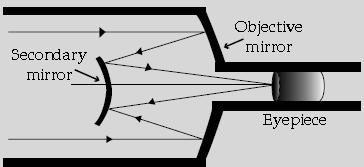
(b) Advantages
(i) Spherical aberration is absent.
(ii) Chromatic aberration is absent.
(iii) Mounting is easier.
(iv) Polishing is done on only one side.
(v) Light gathering power is more.

Question. An optical instrument uses an objective lens of power 100 D and an eyepiece of power 40 D. The final image is formed at infinity when the tube length of the instrument is kept at 20 cm.
(a) Identify the optical instrument.
(b) Calculate the angular magnification produced by the instrument. 
Answer. (a) The instrument is called compound microscope because the focal length of objective lens is smaller than the focal length of eyepiece.
(b) Power of objective = P_o = 100 D

Question. A symmetric biconvex lens of radius of curvature R and made of glass of refractive index 1.5, is placed on a layer of liquid placed on top of a plane mirror as shown in the figure. An optical needle with its tip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself. The distance of the needle from the lens is measured to be x. On removing the liquid layer and repeating the experiment, the distance is found to be y. Obtain the expression for the refractive index of the liquid in terms of x and y.

Answer. Lens maker’s formula
Formula for ‘combination of lenses’ 
Obtaining the expression for μ
(a) Let m1 denote the refractive index of the liquid. When the image of the needle coincides with the lens itself; its distance from the lens, equals the relevant focal length.
With liquid layer present, the given set up is equivalent to a combination of the given (convex) lens and a concavo plane/plano concave liquid lens’.

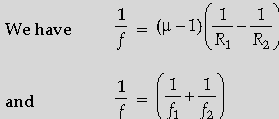
Long Answer Type Questions

Question. Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3 . How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?

Answer. ∠C = 60°
∠B = 90°
∠A = 30°
∴ Angle of incidence at the face AB = 30°

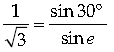
or, sin e = √3 sin30° = √3 × 1/2 = 0.87
∴ e = sin–1 0.87 = 60.46°
Now, the prism is immersed in a liquid of refractive index 1.3. 
The refractive index of the surrounding medium is now greater than that of air but less than that of the medium of prism. Now, the angle of emergence be less than 60.46°.

Question. (a) Two thin lenses are placed coaxially in contact.
Obtain the expression for the focal length of this combination in terms of the focal lengths of the two lenses.
(b) A converging lens of refractive index 1.5 has a power of 10 D. When it is completely immersed in a liquid, it behaves as a diverging lens of focal length 50 cm. Find the refractive index of the liquid.
Answer. (a) Consider two thin lenses L1 and L2 of focal length f1 and f2 are placed coaxially in contact with each other.
The lenses are so thin that their optical centres are assumed to coincide at point P.

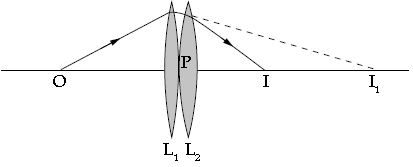
An object is placed at O on the common principal axis. The lens L1 produces an image at I₁ and this image acts as the object for the second lens L₂. The final image is produced at I as shown in the above figure.
PO = u, object distance for the first lens (L₁),
PI = v, final image distance and
PI₁ = v₁, image distance for the first lens (L₁) = object distance for second lens (L₂).

Question. (a) Under what conditions is the phenomenon of total internal reflection of light observed ? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
(b) Three lenses of focal lengths +10 cm, –10 cm and +30 cm are arranged coaxially as in the figure given below.

(c) Find the position of the final image formed by the combination.
Answer. (a) Two conditions of total internal reflection
(b) Obtaining the relation 1
(c) Calculating of the position of the final image 
(a) (i) Light travels from denser to rarer medium.
(ii) Angle of incidence is more than the critical angle 
(b) For the Grazing incidence,

Question. (a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index μ of the material of prism in terms of the angle of prism A and angle of minimum deviation δm.
(b) A ray of light PQ enters an isosceles right-angled prism ABC of refractive index 1.5 as shown in figure.

(i) Trace the path of the ray through the prism.
(ii) What will be the effect on the path of the ray if the refractive index of the prism is 1.4 ?
Answer. (a)

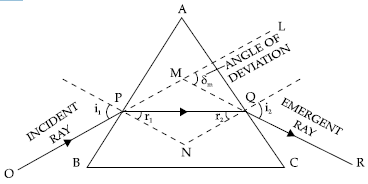
OP is the incidence ray on the prism and QR
emergent ray.
∠i₁ = Angle if incidence
∠i₂ = Angle of emergence
A = Angle of the prism
μ = Refractive index of the material of the prism
δ = Angle of deviation
For minimum deviation, ∠r₁ = ∠r₂ = ∠r
A = ∠r₁ +∠r₂
So, A = ∠r +∠r = ∠2r
∠r = A / 2
Also, ∠i₁ +∠i₂ = ∠i

So, the ray which is incident on AB surface will be reflected making an angle 45°.
The angle of incidence on AC surface is also 45°; so, the ray will be reflected making an angle 45°.
The ray is incident normally on the surface BC. So, there will be no deviation due to refraction.
(ii) If μ = 1.4, then the critical angle
sin-1 = 1/1 4 = 45.23
So, the ray will be refracted out from the AB face.

Question. (a) Plot a graph to show variation of the angle of deviation as a function of angle of incidence for light passing through a prism. Derive an expression for refractive index of the prism in terms of angle of minimum deviation and angle of prism.
(b) What is dispersion of light? What is its cause?
(c) A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in fig. What must be the minimum value of refractive index of glass? Give relevant calculations.

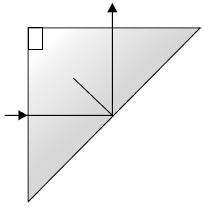
Answer. (a) Plot showing the variation of the angle of deviation as a function of angle of incidence Derivation of expression of refractive index 
(b) Definition of dispersion and its cause 
(c) Calculation of minimum value of refractive index

(b) The phenomenon of splitting of white light into its constituent colours.
Cause: Refractive index of the material is different for different colours. According to the equation, δ = (μ – 1)A, where A is the angle of prism, different colours will deviate through different amount.

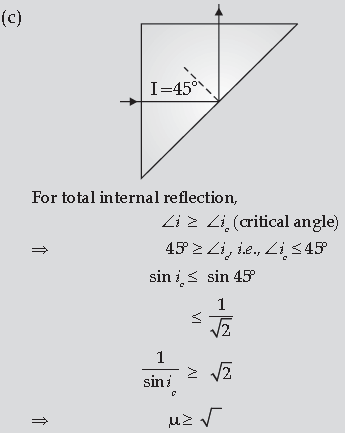
Hence, the minimum value of refractive index must be √2

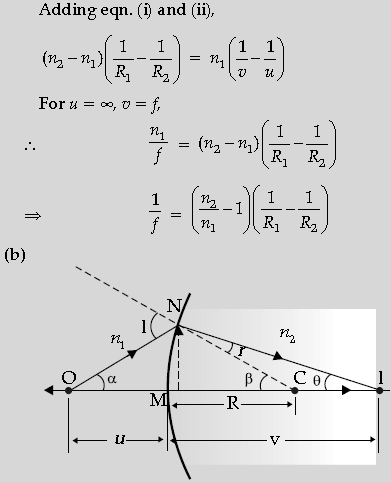
Question. (a) Derive the mathematical relation between refractive indices n₁ and n₂ of two radii and radius of curvature R for refraction at a convex spherical surface. Consider the object to be a point since lying on the principle axis in rarer medium of refractive index n₁ and a real image formed in the denser medium of refractive index n₂. Hence, derive lens maker’s formula.
(b) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20 cm. The distance of light source from the glass surface is 100 cm. At what position is the image formed?
Answer.

Question. (a) Draw the ray diagram showing refraction of light through a glass prism and hence obtain the relation between the refractive index m of the prism, angle of prism and angle of minimum deviation.
(b) Determine the value of the angle of incidence for a ray of light travelling from a medium of refractive index µ₁ = √2 into the medium of refractive index µ₂ = 1, so that it just grazes along the surface of separation.
Answer. (a)

From fig., ∠A + ∠QNR = 180° …(i)
From triangle ΔQNR, r₁ + r₂ + QNR = 180° …(ii)
From eqn. (i) & (ii)
∴ ∠A = r₁ + r₂ ½
The angle of deviation,
δ = (i – r₁) + (e – r₂)
= i + e – A
At minimum deviation, i = e and r₁ = r₂