Assignments For Class 10 Mathematics Linear Equations

Assignments for Class 10 Mathematics Linear Equations have been developed for Standard 10 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 10 Mathematics Linear Equations from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 10 Mathematics Linear Equations. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Linear Equations book and get good marks in class 10 exams.

Question. If the system of equation3x + y =1,(2k -1) x +(k -1) y = (2k +1) , has no solution, then the value of k is:   
(A) 2
(B) 3
(C) – 2
(D) 1

Question. If x – y = 3and x + y ≥ 9the least value of ‘ x ‘ is:   
(A) 6
(B) 3
(C) 2
(D) 1

Question. Two numbers are in the ratio 3: 4. If 5 is subtracted from each .then the ratio will be 2:3. What is the smallest number?   
(A) 15
(B) 18
(C) 20
(D) 24

Question. The present age difference between father and son is 14 years. The ratio of their age will be 4:3 after 11 years. How old is son now? 
(A) 25 years
(B) 31 years
(C) 28 years
(D) 30 years

Question. Five years ago the sum of ages of the father and the son was 40 years. In present it’s ratio is 4:1, then the present age of father is………..   
(A) 30 years
(B) 40 years
(C) 45 years
(D) 42 years

Question. The sum of two numbers is 100 and one number is two less than twice the other number. Then the numbers are   
(A) 34, 66
(B) 24, 76
(C) 44, 56
(D) 46, 54

Question. The value of K if the linear equations x + 2y = 3 and 5x + ky + 7 = 0 has unique solution is 
(A) K ≠ 1
(B) K ≠ 10
(C) K ≠ 5
(D) K ≠ 15

Question. 3-years ago, the sum of ages of a father and his son were 40 years. After 2-year, the sum of ages of the father and his son will be__________   
(A) 40
(B) 46
(C) 50
(D) 56

Question. A boat goes 16 km upstream and 24 km downstream in 6 hours. Also it covers 12 km up stream and 36 km downstream in the same time. Find the speed of the boat in still water?
(A) 8 km/h
(B) 4 km/h         
(C) 2 (1/2) km/h
(D) None of these

Question. Sum of the digits of two digit number is 9. The number obtained by interchanging the digit is 18 more than twice the original number. The original number is:   
(A) 72
(B) 27
(C) 36
(D) 63

CBSE Class 10 Mathematics Linear Equations Assignment Set A

CBSE Class 10 Mathematics Linear Equations Assignment Set B

CBSE Class 10 Mathematics Linear Equations Assignment Set D

CBSE Class 10 Mathematics Linear Equations Assignment Set E

CBSE Class 10 Mathematics Linear Equations Assignment Set G

CBSE Class 10 Mathematics Linear Equations Assignment Set H

CBSE Class 10 Mathematics Linear Equations Assignment Set I

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set A

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set B

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set C

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set D

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set E

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set F

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set G

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set H

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set I

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set J

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set K

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set L

CBSE Class 10 Mathematics Pair Of Linear Equations In 2 Variables Assignment Set M

Two linear equations in the same two variables are said to form a pair of linear equations in two variables.

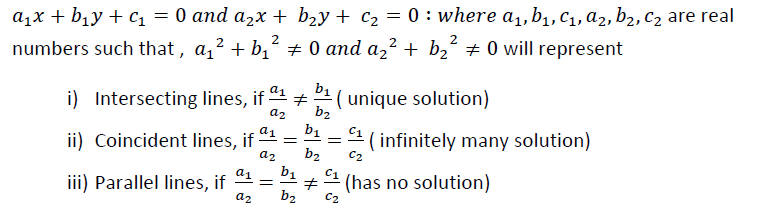
Solution of pair of linear equations

Graphical Method :

• If the lines intersect at a point-unique solution : pair of equations are consistent.
• If the lines coincide-pair of equations are dependent.
• If the lines are parallel-no solution pair of equations are inconsistent.

Algebraic Method:

• Substitution method
• Elimination method and Cross-multiplication method also.

Solved Problems on Class 10 Linear Equations

Question. Solve the following pairs of equations:

sol.

Question. When will the system kx – y = 2 and 6x – 2y = 3 has a unique solution only? 
Solution. A pair of linear pair has unique solution only
when, a₁/ a₂ ≠ b₁/ b₂
Then, k/6 ≠ -1/-2
So, k ≠ 3.

Question. Find the solution of x + y = 3 and 7x + 6y = 2.
Solution. x + y = 3 gives, y = 3 – x …(i)
So, 7x + 6y = 2 gives 7x + 6 (3 – x) = 2
⇒ 7x + 18 – 6x = 2
i.e. x = –16
From (i), y = 3 + 16 = 19
Thus, x = –16 and y = 19 is the required solution.

Question. Find the value(s) of k for which the pair of equations
{kx + 2y = 3/ 3x + 6y = 10} has a unique solution. 
Solution. Given: pair of equation is kx + 2y = 3
3x + 6y = 10
For a unique solution, a₁/ a₂ ≠ b₁/ b₂
Here, a₁ = k, b₁ = 2
a₂ = 3, b = 6
∴ k/ 3 ≠ 2/ 6
∴ k ≠ 1
Hence, the pair of equation has a unique solution for all real values of k except 1

Question. Write the relationship between the coefficients, if the following pair of equations are inconsistent.
ax + by + c = 0; a’x + b’y + c’ = 0.
Solution. The required relationship is:
a/ a’ = b/ b’ = c/ c’

Question. The larger of two supplementary angles exceeds the smaller by 18º. Find the angles.
Solution. Let, the smaller angle be ‘x’ and the larger angle be ‘y’. According to the given conditions:
y = x + 18°
or – x + y = 18° …(i)
and x + y = 18° …(ii)
(Sum of the supplementary angles is 180°) Now, on adding equation (i) and (ii), we get:

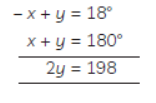
⇒ y = 90°
Put the value of y in equation (i), we get
– x + 99 = 18°
⇒ x = 99 – 18°
= 81°
Hence, the two supplementary angles are 81° and 99°.

Question. In a ΔABC, ∠A = x°, ∠B = 3x° and ∠C = y°. If 3y° – 5x° = 30° prove that the triangle is right angled.
Solution. We know that,
∠A + ∠B + ∠C = 180°
(Sum of interior angles of triangle ABC is 180°)

Question. Find c if the system of equations cx + 3y + (3 – c) = 0; 12x + cy – c = 0 has infinitely many solutions?
Solution. Given equation is:
cx + 3y + (3 – c) = 0
12x + cy – c = 0
Condition for equations to have infinitely many solutions is:

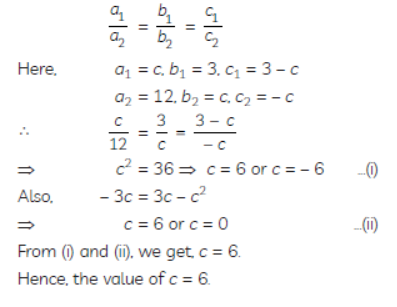
Question. In the figure, ABCD is a rectangle. Find the values of x and y.

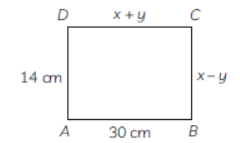
Solution. Given: ABCD is a rectangle

and AB = 30 cm
BC = x – y
CD = x + y
DA = 14 cm
But the opposite sides of rectangle are equal.
∴ AB = CD
x + y = 30 …(i)
and BC = AD
x – y = 14 …(ii)
On adding the equation (i) and (ii), we get:

If we put the value of x in equation (i), we get:
22 + y = 30
⇒ y = 8
Hence, the value of ‘x’ and ‘y’ are 22 and 8, respectively.

Question. For what value of k, does the system of linear equations
2x + 3y = 7
(k – 1) x + (k + 2) y = 3k
have an infinite number of solutions ?
Solution. The given system of linear equation is :

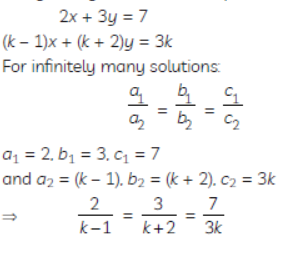
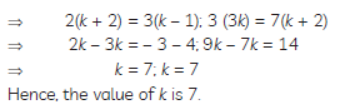
Question. The line represented by x = 7 is parallel to the x-axis. Justify whether the statement is true or not. 26
Solution. False the line represented by x = 7 is not parallel to the x-axis.
Explanation: the line represented by x = 7 is of the form x = a. The graph of the equation is a line parallel to the y-axis and perpendicular to the x-axis.

Question. If 2x + y = 23 and 4x – y = 19, find the values of 5y – 2x and x/ y – 2.
Solution. The given equations are
2x + y = 23 …(i)
4x – y = 19 …(ii)
On adding both equations, we get
⇒ 6x = 42
⇒ x = 7
Putting the value of x in eq. (i), we get
⇒ 2(7) + y = 23
⇒ y = 23 – 14
⇒ y = 9
We have 5y – 2x = 5(9) – 2(7)
= 45 – 14
= 31
and y/x – 2 = 9/7 –2
= – 5/7
Hence, the values of (5y – 2x) and y/x – 2 are 31 and –5/7 respectively.

Question. A fraction becomes 1/ 4 when 1 is subtracted from the numerator and it becomes 1/ 4 when 8 is added to its denominator. Find the fraction.
Solution. Let the fraction be a/ b
Then, according to the question,
a−1/b = 1 4and a/ b+8 = 1/4 
⇒ 3a – b = 3 and 4a – b = 8
On solving these equations, we get:
a = 5, b = 12.
So, the fraction is 5/ 12

Question. In the figure, ABCDE is a pentagon with BEllCD and BCllDE. BC is perpendicular to CD. AB = 5 cm, AE = 5 cm, BE = 7 cm, BC = x – y and CD = x + y. If the perimeter of ABCDE is 27 cm. Find the value of x and y, given x, y ≠ 0

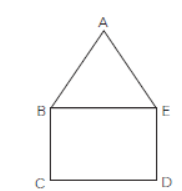
Solution. x + y = 7 and 2(x − y) + x + y + 5 + 5 = 27
⇒ x + y = 7 and 3x − y = 17
Solving, we get, x = 6 and y = 1.

Question. For which value(s) of λ do the pair of linear equations λx + y = λ₂ and x + λy = 1 have:
(A) no solution?
(B) infinitely many solutions?
(C) a unique solution?
Solution. The given pair of linear equations is
λx + y – λ₂ = 0
and x + λy – 1 = 0
Comparing with a1x + b1y + c1 = 0 and
a₂x + b₂y + c₂ = 0, we have
a₁ = λ, b₁ = 1, c₁ = -λ₂;
a₂ = 1, b₂ = λ, c₂ = -1:
a1/ a2 = λ/1 : = b₁/b₂ = 1/λ : c1/c2 = -λ²/ -1= λ²/1
(A) For no solution,

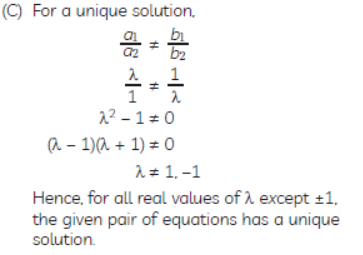
Question. For which values of a and b will the following pair of linear equations have infinitely many solutions?
x + 2y = 1
(a – b)x + (a + b)y = a + b – 2
Solution. The given pair of linear equations is
x + 2y = 1
and (a – b) x + (a + b) y = a + b – 2
x + 2y – 1 = 0
and (a – b)x + (a + b)y – (a + b – 2) = 0
Comparing with a1x + b1y + c1 = 0 and
a₂x + b₂y + c₂ = 0, we have
a₁ = 1, b₁ = 2, c₁ = -1
a2 = (a – b), b₂ = (a + b), c₂ = -(a + b – 2)

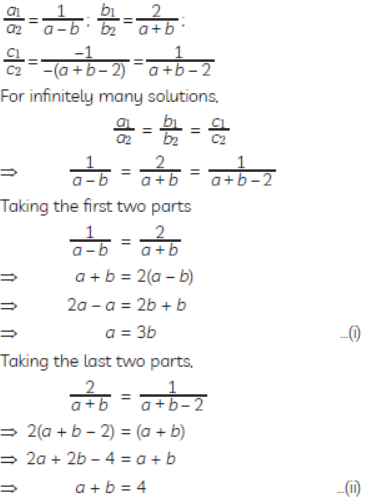
Putting the value of a from eq. (i) in eq. (ii), we get
⇒ 3b + b = 4
⇒ 4b = 4
⇒ b = 1
Putting the value of b in eq. (i), we get
a = 3(1) = 3
The values (a, b) = (3, 1) satisfies all the parts.
Hence, the required values of a and b are 3 and 1 respectively for which the given pair of linear equations has infinitely many solutions.

Question. Write a pair of linear equations which has the unique solution x = 1, y =3. How many such pairs can you write? 
Solution. We know that the condition for the pair of system to have a unique solution is
a₁/ a₂ ≠ b₁/ b₂
Let the equations be
a₁x + b₁y + c₁ = 0
a2x + b2y + c2 = 0
It is given that x = –1 and y = 3 is the unique
solution of these two equations, then it must
satisfy the above equations.
⇒ a₁(–1) + b₁(3) + c1 = 0
⇒ – a1 + 3b1 + c1 = 0 …(i)
and a₂(– 1) + b₂(3) + c₂ = 0
⇒ – a₂ + 3b₂ + c₂ = 0 …(ii)
The restricted values of a₁, a₂ and b₁, b₂ are only
a₁/a₂ = b₁/ b₂
So, all the real values of a₁, a₂, b1, b₂ except those which satisfy eq. (iii) and satisfy eq. (i), and eq. (ii) will have the solution x = –1 and y = 3.
Hence, infinitely many pairs of linear equations are possible

Question. Solve the pair of equations: 42

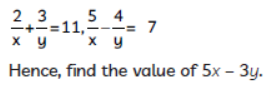
Solution. Given equations are

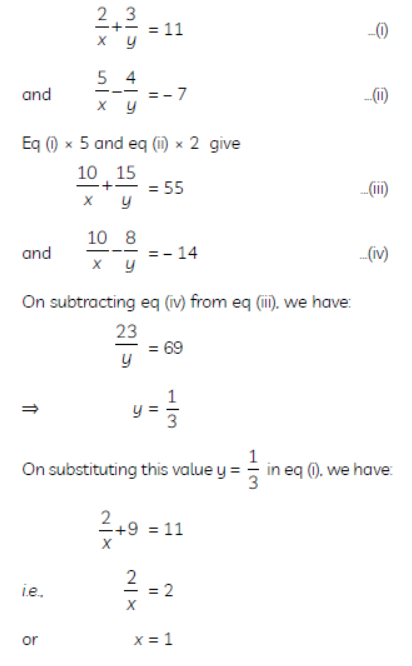
Question. Find the solution of the pair of equations x/10 + y/5 – 1 = 0 and 5/4 = 15. Hence, find λ, if y = λx + 5. 43
Solution. The given pair of equations is

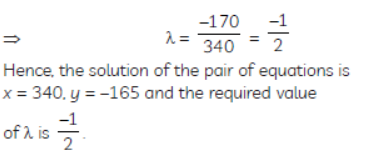
Question. By the graphical method, find whether the following pairs of equations are consistent or not. If consistent, solve them.
(A) 3x + y + 4 = 0 and 6x – 2y + 4 = 0
(B) x – 2y = 6 and 3x – 6y = 0
(C) x + y = 3 and 3x + 3y = 9
Solution. (A) 3x + y + 4 = 0 and 6x – 2y + 4 = 0
The given pair of equations is
3x + y + 4 = 0
and 6x –2y + 4 = 0
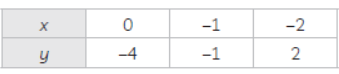
In 3x + y + 4 = 0
y = –4 – 3x
When x = 0, then y = –4
When x = –1, then y = –1
When x = –2, then y = 2

And 6x –2y + 4 = 0
y = 3x + 2
When x = 0, then y = 2
When x = – 1,then y = –1
When x = 1, then y = 5

Plotting the points B(0, –4) and A(–2, 2), we
get the straight line AB.
Plotting the points Q(0, 2) and P(1, 5) we
get the straight line PQ.
The lines AB and PQ intersect at C(–1, –1).

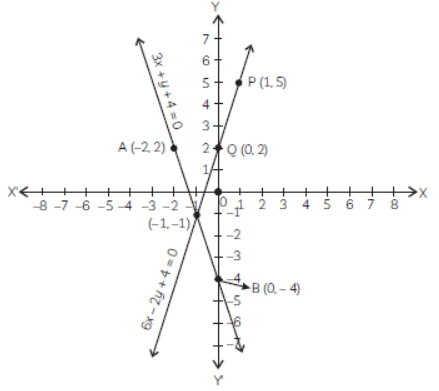
Thus, the pair of equations is consistent and
has solution x = –1, y = –1.
(B) x – 2y = 6 and 3x – 6y = 0
The given pair of equations is
x – 2y = 6 and 3x – 6y = 0
∴ x – 2y = 6

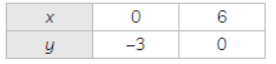
and 3x – 6y = 0

Plotting the points A(0, –3) & B(6, 0), we get line AB.
Again plotting the points P(0, 0) & Q(2, 1) we get line PQ.

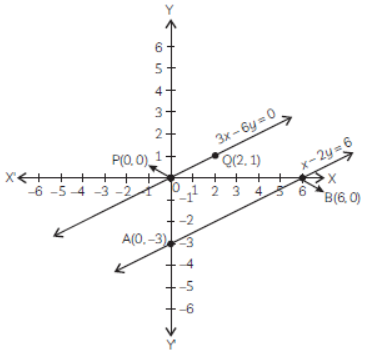
Since, the lines are parallel, the pair of
equations is inconsistent.
(C) x + y = 3 and 3x + 3y = 9
The given pair of equations is
x + y = 3 and 3x + 3y = 9
Now, x + y = 3
⇒ y = 3 – x
If x = 0, then y = 3
If x = 3, then y = 0
If x = 2, then y = 1

and 3x + 3y = 9
⇒ y = (9 – 3x ) /3
If x = 0 then y = 3
if x = 1, then y = 2
if x = 3, then y = 0.

Plotting the points A(0, 3) and B(3, 0), we get the line AB.
Again, plotting the points A(0, 3) and D(1, 2) and B(3, 0), we get the line ADB.

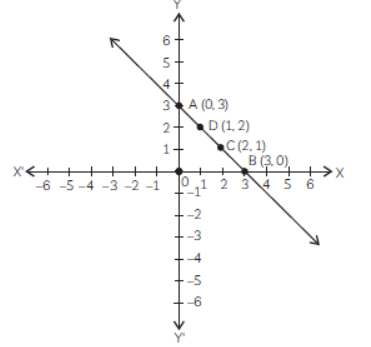
Since, the two lines are coincident, the pair of equations is consistent with infinitely many solutions.

Question. The present age of a father is three years more than three times the age of his son. Three years hence the father‘s age will be 10 years more than twice the age of the son. Determine their present ages. 
Solution. Let ‘x’ (in years) be the present age of the father and ‘y’ (in years) be the present age of the son. Then, according to the given question:
x = 3y + 3 or x – 3y = 3 …(i)
After 3 years,
Father’s age = x + 3, son’s age = y + 3
and x + 3 = 2 (y + 3) + 10
or x – 2y = 13 …(ii)
On solving the two equations, we get:
y = 10, and x = 33.
Thus, the father’s present age is 33 years and the son’s present age is 10 years

Question. Taxi charges in a city consist of fixed charges and the remaining charges depend upon the distance travelled. For a journey of 10 km, the charge paid is ₹ 75 and for a journey of 15 km, the charge paid is ₹ 110. Find the the fixed charge and charges per km. also, find the charges of covering a distance of 35 km.
Solution. Let the fixed charge be ₹ x and charges for per km be ₹ y.
As per the question,
x + 10y = 75 and x + 15y = 110
On solving the two equations, we get
x = 5, y = 7
thus, the fixed charge is ₹ 5 and the charge per km is ₹ 7.
Hence, charge for 35 km is ₹ [5 + 35(7)], i.e., ₹ 250.

Question. Write an equation for a line passing through the point representing solution of the pair of linear equations x + y = 2 and 2x – y = 1. How many such lines can we find? 
Solution. The given equations are
x + y = 2 …(i)
2x – y = 1 …(ii)
Adding eq. (i) and (ii), we have
3x = 3 ⇒ x = 1
Substituting x = 1 in eq. (i), we have y = 1
So, the solution is x = 1 and y = 1 and the
point that represents the solution is (1, 1).
We also know that an infinite number of lines can pass through a given point, say (1, 1). Hence, infinite lines can pass through the intersection point of the linear equations
x + y = 2 and 2x – y = 1 i.e., PE(1, 1).

Question. A man can row a boat downstream 20 km in 2 hours and upstream 4 km in 2 hours. Find his speed of rowing in still water. also find the speed of the stream.
Solution. Let the speed of the stream be ‘x’ km/h’ and the speed of rowing in still water be ‘y’ km/h.
Then, the speed of rowing in the downstream is ‘x + y’ km/h.
And the speed of rowing in the upstream is ‘y – x ‘ km/h
As per the question:
question:
4 /y − x = 2 and 4/ y − x = 2 
⇒ x + y = 10 and y – x = 2
On solving the two equations, we get:
x = 4 and y = 6
thus, the speed of rowing in still water is ‘km/h,
and the speed of the stream is 4 km/hr.

Question. The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°. Find x and y. 
Solution. It is given that x, y and 40° are the angles of a triangle.
We know that the sum of all the angles of a
triangle is 180°
⇒ x + y + 40 = 180
⇒ x + y = 140 …(i)
Also, it is given that the di􀇖erence of angles x and y is
x – y = 30 …(ii)
Adding eq. (i) and (ii), we get
(x + y ) + (x – y) = 140 + 30
⇒ 2x = 170
⇒ x = 85
Putting the value of x in eq. (i), we get
⇒ 85 + y = 140
⇒ y = 140 – 85
y = 55
Hence, the required values of x and y are 85° and 55° respectively.

Question. There are some students in two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from A to B. But, if 20 students are sent from B to A, the number of students in A becomes double the number of students in B. Find the number of students in the two halls.
Solution. Let the number of students in hall A and B be x and y respectively.
By the given condition, to make the number of students equal in each hall, 10 students are sent from A to B
⇒ x – 10 = y + 10
⇒ x – y = 20 …(i)
Also, it is given that if 20 students are sent from B to A, the number of students in A becomes double the number of students in A
⇒ (x + 20) = 2(y – 20)
x – 2y = –60 …(ii)
Subtracting eq. (ii) from eq. (i), we get
(x – y) – (x –2y) = 20 – (–60)
⇒ y = 20
Putting the value of y in eq. (i), we get
x – 80 = 20
⇒ x = 100
Hence, 100 students are in hall A and 80 students are in hall B.

Question. In a competitive examination, one mark is awarded for each correct answer, while 1/2 mark is deducted for every wrong answer. Rahul answered 120 questions and got 90 marks. How many questions did he answer correctly?
Solution. Let x be the number of correct answers,
then, marks awarded for correct answer = x ×1 = x
Total no. of Questions attempted = 120
Number of wrong answers = (120 – x)
Marks deducted for wrong answers
= (120 – x) × 1/2 = x 120 – x/2
Total marks awarded to Rahul = 80
⇒ x – (120 – x/ 2) = 90
⇒ x + x/2 – 6 = 90
+ – 60 = 90
⇒ 3x/2 = 150
⇒ x = 150×2/3
⇒ x = 100
Hence, Rahul answered 100 questions correctly.

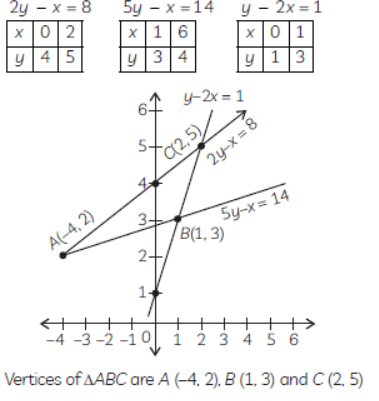
Question. Determine graphically the coordinates of the vertices of a triangle, the equations of whose sides are given by 2y – x = 8, 5y – x = 14 and y – 2x = 1.
Solution.

Question. A part of monthly hostel charges in a college hostel are fixed and the remaining depends on the number of days one has their meals in the mess. When a student A takes food for 25 days, he has to pay ₹ 4,500, whereas a student B who takes food for 30 days has to pay ₹  5,200. Find the fixed charges per month and the cost of food per day.   
Solution. Let, the fixed charge per student = ₹  x
Cost of food per day per student = ₹ y
According to the given condition,
x + 25y = 4500 …(i)
x + 30y = 5200 …(ii)
In subtracting equation (i) from equation (ii), we get

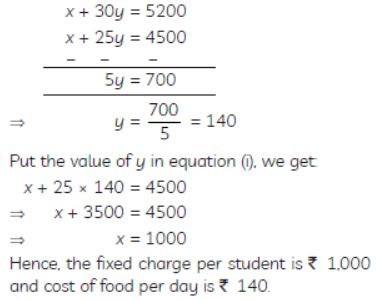
Question. Solve the following system of equations:
21/x + 47/y  = 110
47/x  + 21/x  = 162, x, y ≠ 0
Sulution. Let 1/x = a and 1/y = b
⇒ 21a + 47b = 110 and 47a + 21b = 162
Adding and subtracting the two equations, we get
a + b = 4 and a − b = 2
Solving the above two equations, we get
a = 3 and b = 1
∴ x = 1/3 and y = 1

Question. The sum of reciprocals of a child’s age (in years) 3 years ago and 5 years from now is 1/ 3 . Find his present age.   
Sulution. Let the present age of the child (in years) be x. Then,

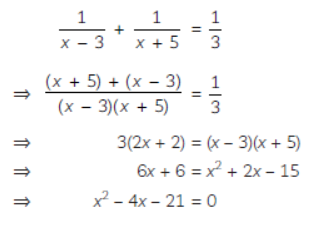
⇒ 3(2x + 2) = (x – 3)(x + 5)
⇒ 6x + 6 = x2 + 2x – 15
⇒ x2 – 4x – 21 = 0
⇒ (x – 7)(x + 3) = 0
⇒ x – 7 = 0 or x + 3 = 0
⇒ x = 7 or x = –3
(x = –3 is a not possible) Thus, her present age is 7 years.

Question. A computer animation below shows a cat moving in a straight line. Its height, h metres, above the ground, is given by 8s – 3h = – 9, where s is the time in seconds after it starts moving. In the same animation, a mouse starts to move at the same time as the cat and its movement is
given by -3s + h = 1.   

(A) Draw the graph of the two e􀆊uations on the same sheet of graph paper;
(B) Will the mouse be able to catch the cat?
(C) If yes, after how much time and at what height?
Sulution. (A) –3s + h = 1
3s – 3h = –9

(B) Yes, if find the several values of the variables s and h for cat as well as mouse, then the same values of s and h show their intersection point. It mean that the cat will definitely catch the mouse.
(C) As mentioned in above statement, the intersection point defines their time and height. Hence, after 6 seconds at a height of 1􀇬 m, the cat will catch the mouse.
After 6 seconds at a height of 19 m.

Question. Find the solution of the pair of equations :   
3/x + 8/y = -1 ; 1/x – 2/y = 2 , x , y ≠ 0
Ans. Given, pair of equation is—

⇒ 3/x = – 1 + 4
⇒ x = 1
Hence, the value of x and y are 1 and – 2 respectively.

Question. A father’s age is three times the sum of the ages of his children. After 5 years, his age will be two times the sum of their ages. Find the present age of the father. 
Sulution. Let the sum of the ages of two children be x years and father’s age be ‘y’ years. According to the given condition:
y = 3x
or y – 3x = 0 …(i)
After 5 years:
Father’s age = (y + 5) years
Sum of the ages of children = (x + 5 + 5) years.
Then, y + 5 = 2(x + 10)
or y – 2x – 15 = 0 …(ii)
on subtracting equation (i) from equation (ii), we get:   

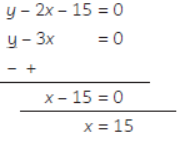
If we put the value of x in equation (i), we get
y – 3 × 15 = 0
⇒ y = 45
Hence, the present age of the father is 45 years.

Question. Ratio between the girls and boys in a class of 40 students is 2 : 3. Five new students joined the class. How many of them must be boys so that the ratio between girls and boys becomes 4 : 5?
Sulution. Let number of girls = 2x
and number of boys = 3x
Total students, 2x + 3x = 40
x = 8
So, number of girls = 2 × 8 = 16
and number of boys = 3 × 8 = 24
Let out of 5 students, y denotes number of boys.
then, number of girls = 5 – y
According to question,
16 + 5 – y/ 24 + y = 4/ 5
5 (21 – y) = 4(24 + y)
105 – 5y = 96 + 4y
9y = 105 – 96
9y = 9
y = 1
So, there must be one boy among five new students.

Question. Sumit is 3 times as old as his son. Five years later, he shall be two and a half times as old as his son. How old is Sumit at present ?   60
Sulution. Let the present age of Sumit’s son be ‘x’ years and the present age of Sumit be ‘y’ years. According to the given conditions:
y = 3x
or – 3x + y = 0 …(i)
Five years later:
Sumit’s son’s age = (x + 5) years
Sumit’s age = (y + 5) years
∴ (y + 5) = 2, 1/ 2 ( x + 5 )
⇒ 2(y + 5) = 5(x + 5)
⇒ 2y + 10 = 5x + 25
⇒ – 5x + 2y = 15 …(ii)
If we multiply equation (i) by 2 and subtract the equation (ii) from (i), we get   

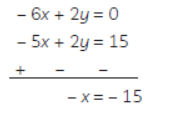
or x = 15
If we put the value of x in equation (i), we get    
– 3 × 15 + y = 0
⇒ y = 45
Hence, Sumit’s present age is 45 years and Sumit’s son’s present age is 15 years.

Question. A two digit number is 4 times the sum of the digits. It is also equal to 3 times the product of the digits. Find the number. 
Sulution. Let the digit at unit’s place be x and at ten’s place be ‘y’.
Then, the number is 10y + x
According to the question,
(10y + x) = 4(x + y)
⇒ 10y + x = 4x + 4y
⇒ 6y – 3x = 0
⇒ – x + 2y = 0
⇒ x = 2y …(i)
and 10y + x = 3xy
∴ 10y + 2y = 3 × 2y × xy 
⇒ 12y = 6y²
⇒ y = 2
∴ x = 4
Hence, the number is 24.

Question. Find the point of intersection of line -3x+7y=3 with x-axis
Solution. (-1,0)

Question. For what value of k the following pair has infinite number of solutions.
(k-3)x+3y=k
K (x + y) =12
Solution. k= 6

Question. Solve the pair of linear equation:
3x – y = 3
7x + 2y = 20
Solution. X = 2, y = 3

Question. Find the value of k so that the lines 2x–3y = 9 and kx – 9y = 18 will be parallel.
Solution. k=6

Question. Find the value of k for which x + 2y = 5,3x + ky+15 = 0 is inconsistent
Solution. k=6

Question. 8 men and 12 boys can finish a piece of work in 10 days while 6 men and 8 boys can finish it in14 Days. Find the time taken by 1 man alone and that by one boy alone to finish the work. 
Solution. One man can finish work in 140 days. One boy can finish work in 280days.

Question. Find the value of K for which the system of linear equations 2x + 5y = 3, (k+1)x + 2(k+2)y = 2 K will have infinite number of solutions.
Solution. K = 3

Question. Solve the pair of linear equation:
px + qy = p – q
q x – py = p + q
Solution. x=1, y = -1

Question. Solve the equation using the method of substitution:
3x – 5y = -1
x – y = – 1
Solution. x = -2 , y = -1

Question. Solve the equations: 1/2x – 1/y = -1 , 1/x + 1/2y = 8  , Where, x ≠ 0 , y ≠ 0
Solution. x = 1/6 , y = -1/6

Question. The sum of digits of a two digit number is 9.If 27 is subtracted from the number, the digits are reversed. Find the number.
Solution. 63

Question. Students of a class are made to stand in rows. If one student is extra in a row, there would be 2rows less. If one student is less in a row there would be 3 rows more. Find the number of the students in the class.
Solution. 60

Question. The owner of a taxi cab company decides to run all the cars he has on CNG fuel instead Of petrol/diesel. The car hire charges in city comprises of fixed charges together with the charge for the Distance covered. For a journey of 12km, the charge paid Rs.89 and for a journey of 20km, the charge paid is Rs.145.
i. What will a person have to pay for travelling a distance of 30km?
ii. Which concept has been used to find it?
iii. Which values of the owner have been depicted here?
Solution. (i) Rs.215,
(ii) A pair of linear equations in two variables has been used to find it.
(iii) Awareness of environment.

Question. Aman travels 370 km partly by train and remaining by car. If he covers 250 km by train and the rest by the car it takes him 4hours, but if he travels 130 km by train and th rest by car, he takes18minutes longer. Find the speed of the train and that of the car.
Solution. Speed of the train=100km/h, speed of the car=80km/h

Question. Given linear equation 2x+3y – 8 = 0, write an other linear equation such that the geometrical representation of the pairs of lines are
(i) intersecting lines, (ii) Parallel Lines.
Solution. (i)4x-3y-8=0(may be another equation also)
(ii) 4x+6y+16 =0 (may be another equation also)

Question. Solve for x and y.
(a-b)x +(a +b)y = a² – 2ab – b²
(a+b)(x+y) = a² + b² 
Solution. X= a+b, y= – 2ab/(a+b)

Question. The sum of two numbers is 8 and the sum of the irreciprocalis 8/15.Find the numbers.
Solution. 3,5

Question. Solve for x and y:
x + y = a + b
ax – by = a² − b²
Q1. X=a y=b

Question. Riya decides to use public transport to cover a distance of 300km.She travels this distance partly by train and remaining by bus. She takes 4 hours if she travels 60 km by bus and the remaining by train. If she travels100kmby bus and the remaining by train, she takes 10minutes more.
i. Finds peed of train and bus separately.
ii. Which concept has been used to solve the above problem?
iii. Which values of Riya have been depicted here?
Solution. (i) The speed of the train = 80 km/h, the speed of the bus = 60km/h
(ii) A pair of linear equations in two variables has been used.
(iii) Controlling the pollution of the environment.

Question. For what value of k will the equation x +5y – 7 = 0 and 4x + 20y + k = 0 represent coincident lines?
Solution. K=-28

Question. Solve graphically:
3x + y + 1 = 0
2x – 3y +8 = 0
Solution. X= -1, y=2

Question. Solve the equations by using the method of cross multiplication:
x – y = 7
5x + 12y =7
Solution. x = 11 , y = -4

Question. A and B each has a certain number of mangoes. A says to B, B If you give 30 of your mangoes, I will have twice as many as left with you.” B replies “If you give me 10, I will have thrice as many as left with you”. How many mangoes does each have?
Sulution. Let number of mangoes with A be x.
Number of mangoes with B be y.
According to the question,
x + 30 = 2 (y – 30)
x + 30 = 2y – 60
x – 2y = –90 …(i)
and y + 10 = 3(x – 10)
y + 10 = 3x – 30
3x – y = 40 …(ii)
Multiplying equation (ii) by 2 and subtracting
from equation (i), we get
–5x = –170
x = 34
Putting x = 34 in equation (i), we get
34 – 2y = –90
– 2y = –90 – 34
– 2y = –124
y = 62
So, number of mangoes with A are 34 and number of mangoes with B are 62.

Question. A man wished to give ` 12 to each person and found that he fell short of ₹ 6 when he wanted to give to all the persons present. He, therefore, distributed ₹ 9 to each person and found that ` 9 were left over. How much money did he have and how many persons were there? 
Sulution. Let, number of persons = x
Money share per person = y
Therefore, total money = ₹ xy
According to the question,
12 × x = xy + 6
12x – 6 = xy …(i)
and 9x = xy – 9
9x + 9 = xy …(ii)
Equating (i) and (ii), we get
12x – 6 = 9x + 9
3x = 15
Put the value of x in equation (i). Then
12 × 5 – 6 = x × y
⇒ xy = 54
So, he have ₹ 54 and there were 5 persons.

Question. It can take 12 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for four hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. How long would it take for each pipe to fill the pool separately ?   
Sulution. Let two pipes A and B of diameter d₁ and d₂
(d₁ > d₂) take x and y hours to fill the pool,

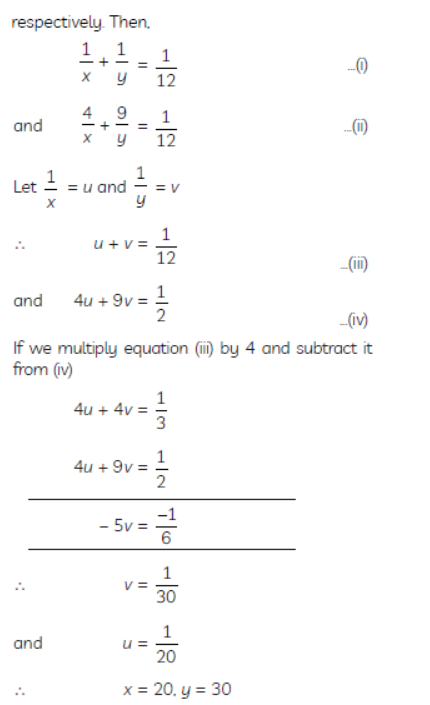
Thus, the pipe with diameter d1 takes 20 hours and the pipe with diamer d2 takes 30 hours to fill the pool alone.

Question. Draw the graphs of the equations x = 3, x = 5 and 2x – y – 4 = 0. also, find the areaof the quadrilateral formed by the lines and  the x-axis.   65
Sulution. The given equation of the lines are
x = 3 x = 5 and 2x – y – 4 = 0
For line,
2x – y – 4 = 0
⇒ y = 2x – 4
If x = 0, y = –4
If x = 2, y = 0
If x = 4, y = 4

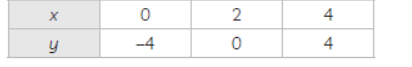
Plotting x = 3 and x = 5 and 2x – y– 4 = 0, we obtain three lines I, II and III respectively, forming a quadrilateral ABCD with the X-axis as shown below:

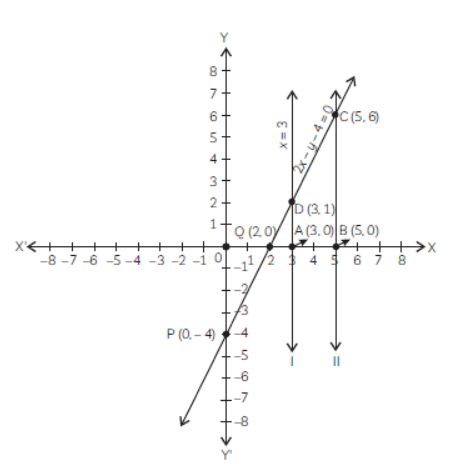
From the graph, we get,
AB = OB – OA = 5 – 3 = 2
AD = 2
BC = 6
We know that the quadrilateral ABCD is a trapezium.
Area of Quadrilateral ABCD 
= 1/2  × (distance between parallel lines)
× (sum of parallel sides)
= 1/2 × (AB) × (AD + BC)
= 1/2 × 2 × (2 + 6)
= 8 sq. units
Hence, the area of the required quadrilateral is 8 square units.

Question. Two water taps together can fill a tank in 17 8 hours. The tap with a larger diameter takes 2 hours less than the tap with the smaller one to fill the tank separately. Find the time in which each tap can fill the tank. 
Sulution. Let the smaller tap fills the tank in x hrs.
∴ The larger tap fills the tank in (x – 2) hrs.
Time taken by both the taps together:
= 15/ 8 hrs.
Now, work done by the smaller tap in an hour:
= 1/ x
Work done by the larger tap in an hour:
= 1/ x − 2

Hence, the smaller tap will fill the tank in 5 hours.
The larger tap will fill the tank in (5 – 2) = 3 hours.

Question. Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour if she travels 2 km by rickshaw and the remaining distance by bus. On the other hand, if she travels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
Sulution. Let the speed of the rickshaw and the bus be x km/hr and y km/hr, respectively.
We know that
speed =  distance/time
and time = distance / speed
Case I:
Time taken by Ankita to travel 2 km by rickshaw,
t₁ = 2/x hr
Remaining distance = 14 – 2 = 12 km
Time taken by Ankita to travel remaining distance, i.e., 12 km by bus,
t₂ = 12/Y hr
It is given that:
Total time taken by rickshaw and bus = 1/2 hr
⇒ t₁ + t2 = 1/2
⇒ 2/c + 12/y = 2 1 …(i)
Case II: 66

Question. A motorboat can travel 30 km upstream and 28 km downstream in 7 hrs. It can travel 21 km upstream and return in 5 hrs. Find the speed of the boat in still water and the speedof the stream.  
Sulution.Let, the speed of the boat in still water = x km/hr
the speed of the stream = y km/hr
∴ the speed of the motorboat upstream = (x – y) km/hr
And the speed of the motorboat downstream
= (x + y) km/hr
Case I:   

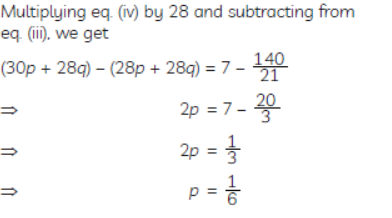
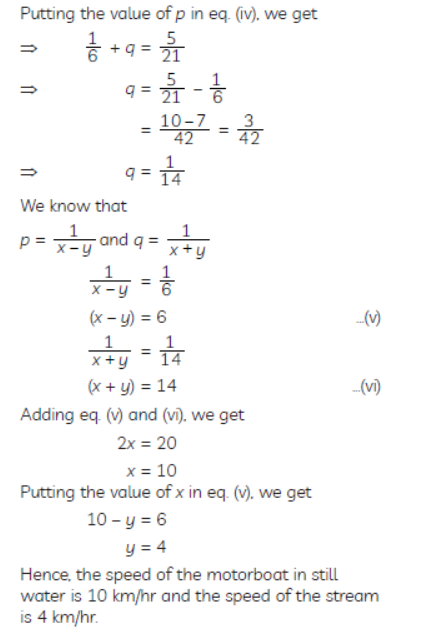
Question. A shopkeeper sells a saree at a profit of 8% and a sweater at a discount of 10%, thereby getting a sum ₹ 1008. If she had sold the saree at a profit of 10% and the sweater at a discount of 8%, she would have got ₹ 1028. Find the cost of the saree and the list price (price before discount) of the sweater. 
Sulution. Let the cost price of a saree = ₹ x
and the list price of sweater = ₹ y
Case I:
(S. P. of saree at 8% profit) + (S.P. of a sweater at 10% discount) = ₹1008
⇒ (100 + 8) % of x + (100 – 10) % of y = 1008
⇒ 108x +  90/ 100 = 1008
⇒ 108x + 90y = 100800
⇒ 6x + 5y = 5600
Multiplying above eq. by 46, we get
⇒ 276x + 230y = 257600 …(i)
Case II:
(S.P. of saree at 10% profit) + (S.P. of a sweater at 8% discount) = ₹1028
⇒ (100 + 10%) of x + (100–8%) of y = 1028
⇒ 110% of x + 92% of y = 1028
⇒ 110x + 92y = 102800
⇒ 55x + 46y = 51400
Multiplying above eq. by 5, we get
⇒ 275x + 230y = 257000 …(ii)
Subtracting eq. (ii) from eq. (i), we get
⇒ (276x + 230y) – (275x + 230y)
= 257600 – 257000
x = 600
Putting the value of x in the above equation,
we get
6x + 5y = 5600
⇒ 6(600) + 5y = 5600
⇒ 5y = 5600 – 3600
⇒ y = 5
2000
⇒ y = 400
Hence, the cost price of the saree and the list price (price before discount) of the sweater are ₹ 600 and ₹ 400, respectively.

Question. Determine, algebraically, the vertices of the triangle formed by the lines
3x – y = 3,
2x – 3y = 2 and
x – 2y = 8 
Sulution. The given equation of lines are:
3x – y = 3 …(i)
2x –3y = 2 …(ii)
x + 2y = 8 …(iii)
Let lines (i), (ii) and (iii) represent the side of a ΔABC i.e., AB, BC and CA respectively.
On solving lines (i) and (ii), we will get the intersection point B.
Multiplying eq. (i) by 3 and then subtracting eq.
(ii), we get
⇒ (9x – 3y) – (2x – 3y) = 9 – 2
⇒ 7x = 7
⇒ x = 1
Putting the value of x in eq. (i), we get
⇒ 3 × 1 – y = 3
⇒ y = 0
Hence, the coordinate of point or vertex B is (1, 0).
On solving lines (ii) and (iii), we will get the intersection point C.
Multiplying eq. (iii) by 2 and then subtracting
eq. (ii), we get
(2x + 4y) – (2x – 3y) = 16 – 2
⇒ 7y = 14
⇒ y = 2
Putting the value of y in eq. (iii), we get
⇒ x + 2(2) = 8
⇒ x = 4
Hence, the coordinate of point or vertex C is (4, 2).
On solving lines (iii) and (i), we will get the intersecting point A.
Multiplying eq. (i) by 2 and then adding eq. (iii), we get
(6x – 2y) + (x + 2y) = 6 + 8
⇒ 7x = 14
⇒ x = 2
Putting the value of x in eq. (i), we get
⇒ 3 × 2 – y = 3
⇒ y = 3
Hence, the coordinate of point or vertex A is (2, 3).
Hence, the vertices of the ΔABC formed by the given lines are A (2, 3), B(1, 0) and C (4, 2).

Question. Ruhi invested a certain amount of money in two schemes A and B, which offer interest atthe rate of 8% per annum and 9% per annum,  respectively. She received ₹ 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received2 more as annual interest. How much money did she invest in each scheme?    69
Ans. Let the money invested in scheme A = ₹ x
and the money invested in scheme B = ₹ y
Case I:
Ruhi invested ₹ x at 8% p.a. + Ruhi invested ₹ y at 9% p.a. and received ₹1860 as annual interest.
We know that simple interest,

Case II:
Ruhi invested ₹ y at 8% p.a. + Ruhi invested
₹ x at 9% p.a. and received ₹ (1860 + 20) as annual interest.
Interest earned when ₹ y invested at 8 % per annum on scheme A,   

Question. Rahul had some bananas and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of ₹ 1 per banana and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per banana and the second lot at the rate of ₹ 4 for 5 bananas, his total collection would have been ₹ 460. Find the total number of bananas he had.
Sulution. Let the number of bananas in lot A = x
and the number of bananas in lot B = y
Case I:
Sold the first lot at the rate of ₹ 2 for 3 bananas + Sold the second lot at the rate of ₹ 1 per banana = Amount received
S.P. of 3 bananas of lot A = ₹ 2
⇒ S.P. of 1 banana of lot A = ₹ 2/3
⇒ S.P. of x bananas of lot A = ₹ 2x /3
S.P. of 1 banana of lot B = ₹ 1
⇒ S.P. of y bananas of lot B = ₹ y
As per given condition
2x/3 + y = 400
2x + 3y = 1200
Case II:
Sold the first lot at the rate of ₹ 1 per banana
+ Sold the second lot at the rate of ₹ 4 for 5
bananas = Amount received
S.P. of 1 banana of lot A = ₹ 1
⇒ S.P. of x bananas of lot A = ₹ x     

Question. The angles of a cyclic quadrilateral ABCD are ∠A = (6x + 10)°, ∠B = (5x)°, ∠C = (x + y)° and ∠D = (3y – 10)°.
Find x and y and hence the values of the four angles. 
Sulution. It is given that,
∠A = (6x + 10°)
∠B = (5x)°
∠C = (x + y)° and
∠D = (3y – 10)°.
We know that by property of cyclic quadrilateral:
Sum of opposite angles = 180°
∠A + ∠C = 180°
⇒ (6x + 10) + (x + y) = 180°
⇒ 6x + 10 + x + y = 180°
⇒ 7x + y = 170° …(i)
Also, ∠B + ∠D = 180°
⇒ 5x + (3y – 10) = 180°
⇒ 5x + 3y = 180° + 10°     

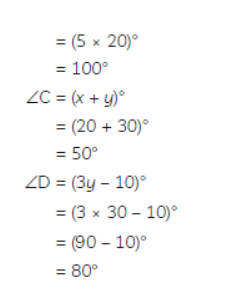
Hence, the required values of x and y are 20° and 30° respectively, and the values of the four angles i.e., ∠A, ∠B, ∠C and ∠D are 130°, 100°, 50°, and 80° respectively.

Question. Given the linear equations 3x -2y +7 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Sol.  (i) 4x + y =1
        (ii) 6x – 4 y +3 = 0
        (iii) 6x – 4 y +14 = 0

Question. A two digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Represent this situation algebraically and geometrically
Sol.  10x + y = 3 + 4(x + y) and 10x + y +18 =10 y + x

Question. On comparing the ratios a1/a2≠b1/b2 , and c1 / c2 , find out whether the following pair of linear equations are consistent or inconsistent. 
(i) 4x-5y=8             (ii) x – 5y = 7
    3×15/4y=6             -3+15y=8
Sol.  (i) consistent
        (ii) inconsistent

Question. The age of the father is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Sol.  40 years 

Question. There are some students in the two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from A and B. But if 20 students are sent from B to A, the number of students in A becomes double the number of students in B. Find the number of students in the two halls.
Sol. 100 students in hall A, 80 students in hall B

Question. Solve graphically each of the following systems of linear equations. Also, find the coordinates of the points where the lines meet the axis of y.
(i)  x+2y-7=0             (ii) 3x + 2y =12
     2x-y-4=0                    5x-2y=4 
Sol.  (i) x = 3, y = 2, (0, 3.5), (0, –4)
       (ii) x = 2, y = 3, (0, 6) and (0, –2)

Question. Solve graphically each of the following systems of linear equations. Also, find the coordinates of the points where the lines meet the axis of x.
(i)  x+2y=5             (ii) 3x + 3y =8
     2x-3y=-4                      x-2y=-3 
Sol.  (i) x = 1, y = 2 (5, 0) (– 2 , 0)
        (ii) x = 1, y = 2, (4, 0), (–3, 0 )

Question. For which value (s) of k will the pair of equations kx +3y = k -3, 12x + ky = k have no solution?
Sol.  k = -6

Question. Find the values of a and b for which the following pair of equations have infinitely many solutions:
(i) 2x +3y = 7 and 2ax + ay = 28 – by
(ii) 2x +3y = 7, (a – b)x +(a + b)y = 3a + b -2
(iii) 2x -(2a +5)y = 5,(2b +1) x -9 y =15
Sol.  (i) a = 4, b = 8     
        (ii) a = 5, b =1     (iii) a =-1 b= 5/2

Question. Write a pair of linear equations which has the unique solution x = 2, y = -3. How many such pairs can you write?
Sol.  x + y +1 = 0, x – y = 5, Infinitely many

Question. If 3x +7y = -1 and 4 y -5x +14 = 0, find the values of 3x -8 y and y/x-2.
Sol. 14, -5/2

Question. Find the solution of the pair of equations x/10+ y/5  -1 = 0 and x/8+y/6  =15. Hence, find λ, if y = λx +5.
Sol.   x = 340 y = -165λ = -1/2

Question. Draw the graph of the pair of equations x -2y = 4 and 3x +5y =1. Write the vertices of the triangle formed by these lines and the y-axis. Also find the area of this triangle.
Sol.  (0,–2), (0 1/5) , (2, –1); 11/5 sq. units

Question. If x +1 is a factor of 2x 3 + ax 2 +2bx +1, then find the values of a and b given that 2a -3b = 4.
Sol. (i) x = 1, y = 2 (5, 0) (– 2 , 0)
       (ii) x = 1, y = 2, (4, 0), (–3, 0 )

Question. The angles of a triangle are x , y and 40°. The difference between the two angles x and y is 30°. Find x and y.
Sol.  x = 85° , y = 55°

Question. The angles of a cyclic quadrilateral ABCD are ∠A = (2x + 4)°, ∠B = (y +3)°, ∠C = (2y +10)°, ∠D = (4x -5)°. Find x and y and hence the values of the four angles.
Sol.  x = 33, y = 50° ,ÐA = 70° ,ÐB = 53° ,ÐC =110° ,ÐD =127°

Question. Half the perimeter of a rectangular garden, whose length is 4m more than its width is 36 m. Find the dimensions of the garden.
Sol. length = 20 m, Breadth = 16 m 

Question. The larger of two supplementary angles exceeds thrice the smaller by 20 degrees. Find them.
Sol. 40°, 140°

Question. Find whether the following pairs of equations are consistent or not by graphical method. If consistent,
solve them.
(i)  x-2y=6             (ii) 5x – 3y = 1           (iii) 4x-7y=-11 
    3×15/4y=6             -3+15y=8                   5x – y+4 =0
Sol. (i) Inconsistent (ii) consistent x = 2, y = -3 (iii) consistent x = -1, y = -1

PRACTICE EXERCISE

Question. A man sold a chair and a table together for Rs. 1520 thereby making a profit of 25% on the chair and 10% on the table. By selling them together for Rs. 1535 he would have made a profit of 10% on the chair and 25% on the table. Find the cost price of each.

Question. The incomes of A and B are in the ratio of 8 : 7 and their expenditures are in the ratio 19 : 16. If each saves Rs. 1250, find their incomes.

Question. Four years ago a mother was four times as old as her daughter. Six years later, the mother will be two-anda- half times as old as her daughter. Determine the present ages of mother and her daughter.

Question. Five years ago, I was thrice as old as my son. Five years hence I shall be twice as old as my son. How old are we now?

Question. Students of a class are made to stand in a rows. If one student is extra in a row, there would be 2 rows less. If one student is less in a row, there would be 3 rows more. Find the number of students in the class.

Question. A man lent a part of money at 10% p.a. and the rest at 15% p.a. His annual income is Rs. 1900. If he had interchanged the rate of interest on two sums, he would have earned Rs. 200 more. Find the amount lent in each case.

Question. 3 bags and 4 pens together cost Rs. 79 whereas 4 bags and 3 pens together cost Rs. 324. Find the total cost of 1 bag and 10 pens.

Question. 4 chairs and 3 tables cost Rs. 2100 and 5 chairs and 2 tables cost Rs. 1750. Find the cost of a chair and a table seperately.

Question. The taxi charges in a city comprise of a fixed charge together with the charge for the distance covered. For a journey of 10 km the charge paid is Rs. 75 and for a journey of 15 km the charge paid is Rs. 110. What will a person have to pay for travelling a distance of 25 km?

Question. Two audio cassetes and three video cassettes cost Rs. 340. But three audio cassettes and two video cassettes cost Rs. 260. Find the price of an audio cassette and that of a video cassette .

Question. On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains Rs. 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss, he gains Rs. 1500 on the transaction. Find the actual prices of T.V. and fridge.

Question. The sum of two numbers is 26 and three times one of them exceeds five times the other by 6. Find the numbers.

Question. Find two numbers such that one-third of the first number added to one-fifth of the second number gives 20 and one-sixth of the first added to one-twelfth of the second gives 9.

Question. The sum of the digits of a two digit number is 12. The number obtained by reversing the order of the digits of the given number exceeds the given number by 18. Find the two digit number. 

Question. In a two digit number, the ten’s digit is three times the unit’s digit. When the number is decreased by 54, the digits are reversed. Find the number.

Question. A two-digit number is such that the product of the digits is 20. If 9 is added to the number, the digits interchange their places. Find the number. 

Question. Two years ago, a father was five times as old as his son. Two years later, his age will be 8 more than three times the age of the son. Find the present age of the father and son. 

Question. Father’s age is three times the sum of ages of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.

Question. A two-digit number is obtained by multiplying the sum of the digits by 8. Also it is obtained by multiplying the difference of the digits by 14 and adding 2. Find the number.

Question. The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. Find the fraction.

Question. The area of a rectangle gets reduced by 80 sq. units if its length is reduced by 5 units and the breadth is increased by 2 units. If we increase the length by 10 units and decrease the breadth by 5 units, the area is increased by 50 sq. units. Find the length and breadth of the rectangle. Problems related to Fixed Salary, Fare etc. 

Question. A fraction becomes 1/3 if 1 is subtracted from both its numerator and denominator. If 1 is added to both the numerator and denominator, it becomes 1/2. Find the fraction.

Question. The denominator of a fraction is 4 more than twice the numerator. When both the numerator and denominator are decreased by 6, then the denominator becomes 12 times the numerator. Determine the fraction. 

Question. If the numerator of a certain fraction is increased by 2 and denominator by 1, the fraction becomes 5/8 , and if the numerator and denominator are each diminished by 1, the fraction becomes 1/2. Find the fraction.

Question. Points A and B are 70 km apart on a highway. A car starts from A and another car starts from B at the same time. If they travel in the same direction, they meet in 7 hours, but if they travel towards each other they meet in one hour. What are their speeds? 

Question. A boat goes 12 km upstream and 40 km downstream in 8 hours. It can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the stream.

Question. The present age of a father is three years more than three times the age of the son. Three years hence father’s age will be 10 years more than twice the age of the son. Determine their present ages. Problems related to Articles and their costs 

Question. A sailor goes 8 km downstream in 40 minutes and returns in 1 hour. Determine the speed of the sailor in still water and the speed of the current.

Question. A man travelled 300 km by train and 200 km by taxi, it took him 5 hours 30 minutes. But if he travels 260 km by train and 240 km by taxi he takes 6 minutes longer. Find the speed of the train and that of the taxi.

Question. A father is three times as old as his son. In 12 years, he will be twice as old as his son. Find the present age of the father and the son.

Question. If in a rectangle, the length is increased and breadth reduced each by 2 units, the area is reduced by 28 sq. units. If, however the length is reduced by 1 unit and the breadth increased by 2 units, the area increases by 33 sq. units. Find the area of the rectangle.

Question. A railway half ticket costs half the full fare and the reservation charge is the same on half ticket as on full ticket. One reserved first class ticket from Mumbai to Ahmedabad costs Rs. 216 and one full and one half reserved first class tickets cost Rs. 327. What is the basic first class full fare and what is the reservation charge?

Question. A part of the monthly expenditure of a family is constant and the remaining varies with the price of wheat. When the rate of wheat is Rs. 250 per quintal, the total monthly expenditure is Rs. 1,000 and when it is Rs. 240 per quintal, the total monthly expenditure of the family is Rs. 980. Find the total monthly expenditure of the family when the cost of wheat is Rs. 350 per quintal.

Question. In a ∠ABC, ∠C = 3∠B and 3∠B = 2 (∠A + ∠B). Find the angles of the triangle.

Question. In a cyclic quadrilateral ABCD, ∠A = (2x + 4)°, ∠B = (y + 3)°, ∠C= (2y + 10)° and ∠D = (4x – 5)°. Find the angles of the cyclic quadrilateral.

Question. Riya has only 50 p and 25 p coins in her purse. If in all she has 210 coins of the total value of Rs. 82.50, find the number of coins of each type.

Question. A person invested some amount at the rate of 12% simple interest and some other amount at 10% simple interest. He received yearly interest of Rs. 130. If he had interchanged the amounts invested, he would have received Rs. 4 as more interest. Find the amount invested in each case.

Question. 8 women and 12 girls can finish a piece of work in 10 days, while 6 women and 8 girls can finish it in 14 days. Find the time taken by one woman alone and that by one girl alone to finish the same work.

Question. In a school, there are only two sections of X students A and B. If 10 students are sent from A to B, the number of students in each room is same. If 20 students are sent from B to A the number of students in A is double the number of students in B. Find the number of students in each room.

Question. A two-digit number is four times the sum of its digits and twice the product of the digits. Find the number.

Question. A number consists of two digits. When it is divided by the sum of the digits, the quotient is 8. The sum of the reciprocals of digits is nine times the product of the reciprocals of the digits. Find number.

Question. Bhavya scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then she would have scored 50 marks. How many questions were there in the test?

Question. Sumit travels 600 km to his home partly by train and partly by car. He takes 8 hours if he travels 120 km by train and the rest by car. He takes 20 minutes longer if he travels 200 km by train and the rest by car. Find the speed of the train and the car.

Question. A and B each have certain number of oranges. A says to B, ‘‘If you give me 10 of your oranges, I will have twice the number of oranges left with you. B replies, ‘‘If you give 10 of your oranges, I will have the same number of oranges as left with you.’’ Find the number of oranges with A and B seperately.

Question. The age of father 8 years back was five times that of his son. After 8 years, his age will be 8 years more than twice the age of his son. Find their present ages.

Question. A number consists of two digits. When it is divided by the sum of the digits, the quotient is 6 with no remainder. When the number is divided by 9, the digits are reversed. Find the number.

Question. The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number. 

Question. A boat can go 20 km upstream and 30 km downstream in 3 hours. It can go 10 km upstream and 20 km downstream in 1, 2/3 hours. Find the speed of the boat in still water and also the speed of the stream.

Assignments for Class 10 Mathematics Linear Equations as per CBSE NCERT pattern

All students studying in Grade 10 Mathematics Linear Equations should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Linear Equations exam for standard 10. We have made sure that all topics given in your textbook for Mathematics Linear Equations which is suggested in Class 10 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.

Some advantages of Free Assignments for Class 10 Mathematics Linear Equations

1. Solving Assignments for Mathematics Linear Equations Class 10 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
2. By solving one assignments given in your class by Mathematics Linear Equations teacher for class 10 will help you to keep in touch with the topic thus reducing dependence on last minute studies
3. You will be able to understand the type of questions which are expected in your Mathematics Linear Equations class test
4. You will be able to revise all topics given in the ebook for Class 10 Mathematics Linear Equations as all questions have been provided in the question banks
5. NCERT Class 10 Mathematics Linear Equations Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
6. Parents will be able to take print out of the assignments and give to their child easily.

All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 10 Mathematics Linear Equations teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Linear Equations Assignments PDF.