Please refer to Assignments Class 9 Mathematics Surface Areas and Volumes Chapter 13 with solved questions and answers. We have provided Class 9 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 13 Surface Areas and Volumes Class 9 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Surface Areas and Volumes Assignments Class 9 Mathematics
Solved Examples
Example: There are twenty-five cuboid-shaped pillars in a building, each of dimensions 1 m ×1 m × 10 m. Find the cost of plastering the surface of all the pillars
at the rate of Rs 16 per m2.
Solution:
Length (l) of one pillar = 1 m
Breadth (b) of one pillar = 1 m
Height (h) of one pillar = 10 m
∴ Lateral surface area of one pillar= 2h (l + b)
= 2 × 10 × (1 + 1) m2
= 40 m2
⇒ Lateral surface area of twenty-five pillars = (25 × 40) m2 = 1000 m2
Cost of plastering 1 m2 of surface = Rs 16
⇒ Cost of plastering 1000 m2 of surface = Rs (16 × 1000) = Rs 16000
Thus, the cost of plastering the twenty-five pillars of the building is Rs 16000.
Example: Find the length of the diagonal of a cube whose surface area is 294 m2.
Solution:
Let the edge of the given cube be a.
∴ Surface area of the cube = 6a2
It is given that the surface area of the cube is 294 m2.
So, 6a2 = 294
⇒ a2 = 49m2
⇒ ∴ a = √49 m = 7m
Now, length of the diagonal of the cube = √3a = 7√3m
Example: A metallic container (open at the top) is a cuboid of dimensions 7 cm × 5 cm × 8 cm. What amount of metal sheet went into making the container? Also, find the cost required for painting the outside of the container, excluding the base, at the rate of Rs 17 per 3 cm2.
Solution:
Length (l) of the container = 7 cm
Breadth (b) of the container = 5 cm
Height (h) of the container = 8 cm
The container is open at the top. Therefore, while calculating the amount of metal sheet
used, we will exclude the top part.
∴ Amount of metal sheet used = Total surface area − Area of the top part
= 2 (lb + bh + lh) − lb
= [2 × (7 × 5 + 5 × 8 + 7 × 8) − 7 × 5] cm2
= [2 × (35 + 40 + 56) − 35] cm2
= (2 × 131 − 35) cm2
= 227 cm2
Thus, 227 cm2 of metal went into making the given container.
Now, area to be painted = Lateral surface area of the cuboid
= 2h (l + b)
= [2 × 8 × (7 + 5)] cm2
= (16 × 12) cm2
= 192 cm2
Cost of painting 3 cm2 of surface = Rs 17
⇒ Cost of painting 1 cm2 of surface = Rs 17/3
⇒ Cost of painting 192 cm2 of surface = Rs (192 x 17/3) = Rs 1088
Therefore, the cost of painting the outside of the container is Rs 1088.
Example: If the total surface area of a cube is 24×2, then find the surface area of the cuboid formed by joining i)two such cubes.
ii)three such cubes.
Solution:
Total surface area of cube = 6a2
It is given that the total surface area of the cube is 24×2.
So, 6a2 = 24×2
⇒ a2 = 4×2
⇒ ∴ a = 2x
So, the edge of the cube is 2x.
i)When two cubes with edge 2x are joined, we obtain the following cuboid.
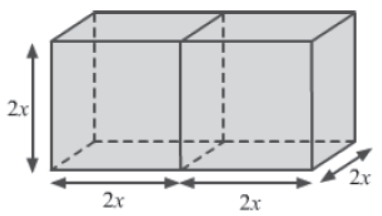
Length (l) of the cuboid = 2x + 2x = 4x
Breadth (b) of the cuboid = 2x
Height (h) of the cuboid = 2x
∴ Surface area of the cuboid = 2 (lb + bh + lh)
= 2 × (4x × 2x + 2x × 2x + 4x × 2x)
= 2 × (8x2 + 4x2 + 8x2)
= 40×2
Thus, the surface area of the cuboid formed according to the given specifications is 40×2.
ii)When three cubes with edge 2x are joined, we obtain the following cuboid. img
Length (l) of the cuboid = 2x + 2x + 2x = 6x
Breadth (b) of the cuboid = 2x
Height (h) of the cuboid = 2x
∴ Surface area of the cuboid = 2 (lb + bh + lh)
= 2 × (6x × 2x + 2x × 2x + 6x × 2x)
= 2 × (12×2 + 4×2 + 12×2)
= 56×2
Thus, the surface area of the cuboid formed according to the given specifications is 56×2.
Example: The cost of flooring a twenty-metre-long room at Rs 5 per square metre is Rs 1000. If the cost of painting the four walls of the room at Rs 15 per square metre is Rs 1800, then find the height of the room.
Solution: The length (l) of the room is given as 20 m. Let b and h be its breadth and height respectively.
Area of the floor = l × b
Cost of flooring at Rs 5 per m2 = Rs 1000
So, 5 × l × b = 1000
⇒ 5 x 20 x b = 1000
⇒ ∴ b = 1000/100 = 10
Area of the four walls = 2 (bh + lh)
Cost of painting the four walls at Rs 15 per m2 = Rs 1800
So, 15 × [2 (bh + lh)] = 1800
⇒ 15 × [2 × (10 × h + 20 × h)] = 1800
⇒ 30 h = 1800/15 x 2
⇒ ∴ h = 1800/15 x 2 x 30 = 2
Thus, the height of the room is 2 m.
Example: The internal measures of a cuboidal room are 20 m × 15 m × 12 m.
Dinesh wants to paint the four walls of the room with orange colour and the roof of the room with white colour. 100 m2 of surface can be painted using each can of orange paint and 125 m2 of surface can be painted using each can of white paint. How many cans of each colour will be required? If the orange and white paints are available at Rs 250 per can and Rs 300 per can respectively, then how much money will be spent by Dinesh to paint the room?
Solution: Length (l) of the room = 20 m
Breadth (b) of the room = 15 m
Height (h) of the room = 12 m
Area of the room to be painted using orange colour= Area of the four walls of the room
= Lateral surface area of the room
= 2h (l + b)
= [2 × 12 (20 + 15)] m2
= (24 × 35) m2
= 840 m2
It is given that 100 m2 of surface can be painted using each can of orange paint.
∴ Number of cans of orange paint required = Area of the room painted using orange colour /Area that can be painted using each can
= 840/100
= 8.4
= 9 (∵ 8 cans will be insufficient for the job)
Thus, 9 cans of orange paint will be required for painting the four walls of the room.
Area of the room to be painted using white colour= Area of the roof
= l × b
= (20 × 15) m2
= 300 m2
It is given that 125 m2 of surface can be painted using each can of white paint.
∴ Number of cans of white paint required = Area of the room painted using white colour /Area that can be painted using each can
= 300/125
= 2.4
= 3 (∵ 2 cans will be insufficient for the job)
Thus, 3 cans of white paint will be required for painting the roof of the room.
Cost of each can of orange paint = Rs 250
⇒ Cost of 9 cans of orange paint = 9 × Rs 250 = Rs 2250
Cost of each can of white paint = Rs 300
⇒ Cost of 3 cans of white paint = 3 × Rs 300 = Rs 900
Thus, total money that will be spent in painting the room = Rs 2250 + Rs 900 = Rs 3150
Example: The curved surface area of a right circular cylinder of height 7 cm is 44 cm2. Find the diameter of the base of the cylinder.
Solution:
Let r be the radius and h be the height of the cylinder.
It is given that:
h = 7 cm
Curved surface area of the cylinder = 44 cm2
So, 2πrh = 44 cm2
⇒ 2 x 22/7 x r x 7 cm = 44 cm2
⇒ r = 44 x 7/2 x 22 x 7 cm
⇒ ∴ r = 1 cm
Thus, diameter of the base of the cylinder = 2r = 2 cm
Example: The radii of two right circular cylinders are in the ratio 4 : 5 and their heights are in the ratio 3 : 1. What is the ratio of their curved surface areas?
Solution:
Let the radii of the cylinders be 4r and 5r and their heights be 3h and h.
Let S1 be the curved surface area of the cylinder of radius 4r and height 3h.
∴ S1 = 2π × 4r × 3h = 24πrh
Let S2 be the curved surface area of the cylinder of radius 5r and height h.
∴ S2 = 2π × 5r × h = 10πrh
Now,
S1/S2 = 24πrh/10πrh = 12/5
⇒ S1 : S2 = 12 : 5
Thus, the curved surface areas of the two cylinders are in the ratio 12 : 5.
Example: Find the height and curved surface area of a cylinder whose radius is 14 dm and total surface area is 1760 dm2.
Solution:
Radius (r) of the cylinder = 14 dm
Let the height of the cylinder be h.
Total surface area of the cylinder = 1760 dm2
So, 2πr (r + h) = 1760 dm2
⇒ 2 x 22/7 x 14(14+h) dm = 1760 dm2
⇒ 14 + h = 1760 x 7/2 x 22 x 14 dm
⇒ 14 + h = 20 dm
⇒ ∴ h = (20-14) dm = 6dm
Thus, the height of the cylinder is 6 dm.
Now, curved surface area of the cylinder = 2πrh
= (2 x 22/7 x 14 x 6) dm2
= 528 dm2
Example: There are ten identical cylindrical pillars in a building. If the radius of each pillar is 35 cm and the height is 12 m, then find the cost of plastering the surface of all the pillars at the rate of Rs 15 per m2.
Solution: Radius (r) of one pillar = 35 cm = 35/100 m = 0.35 m
Height (h) of one pillar = 12 m
∴ Curved surface area of one pillar = 2πrh
= (2 x 22/7 x 0.35 x 12) m2
= 26 .4 m2
⇒ Curved surface area of ten pillars = 10 × 26.4 m2 = 264 m2
Cost of plastering 1 m2 of surface = Rs 15
⇒ Cost of plastering 264 m2 of surface = Rs (15 × 264) = Rs 3960
Therefore, the cost of plastering the ten pillars of the building is Rs 3960.
Example: A cylindrical road roller is of diameter 175 cm and length 1.5 m. It has to cover an area of 0.33 hectare on the ground. How many complete revolutions must the roller take to cover the ground? (1 hectare = 10000 m2)
Solution: Diameter of the cylindrical roller = 175 cm 175/100 m = 7/4 m
∴ Radius (r) of the cylindrical roller = 7/8 m
Length (h) of the cylindrical roller = 1.5 m
Area covered by the roller in one complete revolution = Curved surface area of the roller
= 2πrh
= (2 x 22/7 x 7/8 x 1.5) m2
= 8.25 m2
Area of the ground to be covered = 0.33 hectare = 0.33 × 10000 m2 = 3300 m2
∴ Number of complete revolutions = Area of the ground covered by the roller/Area of the covered by the roller in one revolution
= 3300 m2/8.25m2
= 400
Thus, the roller must take 400 complete revolutions to cover the ground.
Example: The internal diameter, thickness and height of a hollow cylinder are 20 cm, 1 cm and 25 cm respectively. What is the total surface area of the cylinder?
Solution: Internal diameter of the cylinder = 20 cm
∴ Internal radius (r) of the cylinder = 20/2 cm = 10 cm
Thickness of the cylinder = 1 cm
∴ External radius (R) of the cylinder = (10 + 1) cm = 11 cm
Height (h) of the cylinder = 25 cm
Internal curved surface area of the cylinder = 2πrh
= (2 x 22/7 x 10 x 25 ) cm2
= 11000/7 cm2
External curved surface area of the cylinder = 2πRh
= (2 x 22/7 x 10 x 25 ) cm2
= 12100/7 cm2
The two bases of the cylinder are ring-shaped. Therefore, their area is given as follows:
Area of base = π (R2 − r2)
= [22/7 (112 – 102)] cm2
= (22/7 x 21) cm2
= 66 cm2
So, total surface area of the cylinder = Internal CSA + External CSA + 2 × Area of base
= (11000 /7 + 12100/7 + 2 x 66) cm2
= (23100/7 + 132) cm2
= (3300 + 132) cm2
= 3432 cm2
Example: The curved surface area of a cone is 1914 cm2 and its base radius is 21 cm. Find
i)the slant height of the cone.
ii)the total surface area of the cone.
Solution:
i)Radius (r) of the cone = 21 cm
Curved surface area of the cone = 1914 cm2
Let the slant height of the cone be l.
∴ πrl = 1914 cm2
⇒ (22/7 x 21 x l) = 1914
⇒ l = 1914/66 cm
⇒ ∴ l = 29 cm
Thus, the slant height of the cone is 29 cm.
ii)Total surface area of the cone = πr (l + r)
= [22/7 x 21 x (29+21)] cm2
= 22/7 x 21 x 50 cm2
= 3300 cm2
Example: The total surface area of a cone is 33264 cm2 and its base radius and slant height are in the ratio 3 : 5. Find the slant height of the cone.
Solution: Let the radius and slant height of the cone be 3x and 5x respectively.
Total surface area of the cone = 33264 cm2
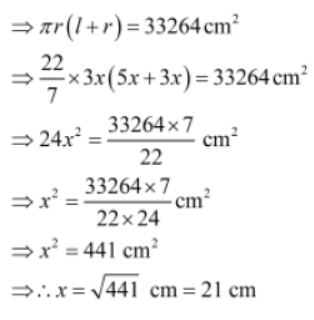
So, slant height of the cone = 5x = 5 × 21 cm = 105 cm
Example: The height and radius of the base of a conical tomb are 8 m and 6 m respectively. Find the cost of whitewashing the outer surface of the tomb at the rate of Rs 2000 per 50 m2.
Solution:
Radius (r) of the conical tomb = 6 m
Height (h) of the base of the conical tomb = 8 m
Let the slant height of the conical tomb be l.
We know that l2 = r2 + h2
⇒ l2 = (62 + 82) m2
⇒ l2 = (36 + 64) m2
⇒ l2 = 100 m2
⇒ ∴ l = √100 m = 10 m
∴ Curved surface area of the conical tomb = πrl
= (22/7 x 6 x 10) m2
= 188.57 m2
Cost of whitewashing 50 m2 of surface = Rs 2000
⇒ Cost of whitewashing 1 m2 of surface = Rs 2000/50 = Rs 40
⇒ Cost of whitewashing 188.57 m2 of surface = 188.57 x Rs 40 = Rs 7542.80
Thus, the cost of whitewashing the outer surface of the tomb is Rs 7542.80.
Example: A corncob (which is shaped like a cone) is of length 30 cm and the radius of its broadest end is 4 cm. If about 5 grains are present per square centimetre of the cob, then approximately how many grains are there on the entire cob?
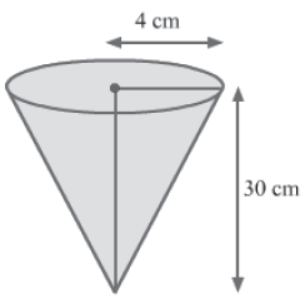
Solution:
Total grains on the cob = Curved surface area of the cob × Number of grains per cm2
Radius (r) of the cob = 4 cm
Height (h) of the base of the cob = 30 cm
Let the slant height of the cob be l.
We know that l2 = r2 + h2
⇒ l2 = (42 + 302) cm2
⇒ l2 = (16 + 900) cm2
⇒ l2 = 916 cm2
⇒ ∴ l = √916 cm = 30.26 cm
Curved surface area of the cob = πrl
= (22/7 x 4 x 30.26) cm2
Total number of grains = 380.4 × 5 = 1902
Thus, there are about 1902 grains on the entire cob.
Example: A cone and a cylinder have the same radius and height. If the ratio of the radius to height is 5 : 12, then find the ratio of the curved surface area of the cone to that of the cylinder.
Solution:
The cylinder and the cone have the same radius and height. Let r be this radius and h be the height.
It is given that:
r/h = 5/12
⇒ r = 5x and h = 12x, where x is any constant
Slant height (l) of the cone = √r2 + h2

Hence, the curved surface areas of the cone and the cylinder are in the ratio 13 : 24.
Example: A cylindrical tent of height 2 m and radius 28 m is surmounted by a right circular cone. If the total height of the tent is 14 m and the cost of papering is Rs 3 per square metre, then calculate the total money spent in papering the inner side of the tent.
Solution:
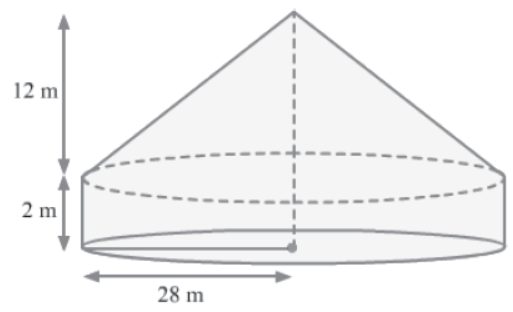
Radius (r) of the cylindrical part = 28 m
Height (h) of the cylindrical part = 2 m
∴ Curved surface area of the cylindrical part = 2πrh
= (2 x 22/7 x 28 x 2) m2
= 352 m2
Radius of the base of the conical part = Radius of the cylindrical part = 28 m
Let H and l be respectively the height and slant height of the conical part.
H = (14 − 2) m = 12 m (âˆμ Total height of the tent = 14 m)
We know that l 2 = r 2 + H 2
⇒ l 2 = (282 + 122) m2
⇒ l 2 = (784 + 144) m2
⇒ l 2 = 928 m2
⇒ ∴ l = √928 m = 30.46 m
∴ Curved surface area of the conical part = πrl
= 22/7 x 28 x 30.46 m2
= 2680.48 m2
Total surface area = Sum of the curved surface areas of the cylindrical and conical parts
= (352 + 2680.48) m2
= 3032.48 m2
Cost of papering 1 m2 of surface = Rs 3
⇒ Cost of papering 3032.48 m2 of surface = Rs 3 × 3032.48 = Rs 9097.44
Thus, the total money spent in papering the inner side of the tent is Rs 9097.44.
Example: What is the radius of a globe whose surface area is 1256 cm2? (Use π = 3.14)
Solution: Let the radius of the globe be r.
Surface area of a sphere = 4πr2
It is given that the surface area of the globe is 1256 cm2.
So, 4πr2 = 1256 cm2
⇒ 4 × 3.14 × r2 = 1256 cm2
⇒ 12.56 × r2 = 1256 cm2
⇒ r2 = (1256/12.56) cm2
⇒ r2 = 100 cm2
⇒ ∴ r = (√100) cm = 10 cm
Thus, the radius of the globe is 10 cm.
Example: Find the surface area of the largest sphere that can be inscribed in a cube of edge 21 cm.
Solution: Edge of the cube = 21 cm
Suppose the largest sphere that can be inscribed in this cube has a radius r.

This sphere will touch all the six walls of the cube. Therefore, the diameter of the sphere will be equal to the edge of the cube.
So, 2r = 21 cm
⇒ r = (21/2) cm
Now, surface area of the required sphere = 4πr2
= (4 x 22/7 x 21/2 x 21/2) cm2
= 1386 cm2
Example: The diameter of a football is approximately 20/19 times the diameter of a volleyball. What is the ratio of their surface areas?
Solution: Let the diameter of the volleyball be x.
∴ Diameter of the football = 20/19 x
Now, radius (r1) of the volleyball = x/2
Radius (r2) of the football = 10/19 x

Thus, the surface areas of the football and the volleyball are in the ratio 400 : 361.
Example: If the diameter of a sphere is increased by 25%, then what will be the percentage increase in its curved surface area?
Solution: Let r be the radius and S be the curved surface area of the sphere.
∴ S = 4πr2
Percentage increase in diameter = 25
∴ Increase in diameter = 25% of 2r = (25/100 x 2r) = r/2
⇒ Increased diameter = 2r + r/2 = 5r/2
∴ Increased radius = 5r/4
Let S ‘ be the new curved surface area of the sphere.
∴ S = 4π(5r/4)2 = 25πr2/4
Now, increase in curved surface area = S’ – S
= 25πr2/4 – 4πr2
= 9πr2/4
∴ Percentage increase in curved surface area = S’ – S/S x 100
= 9πr2/4/4πr2 x 100
= 900/16
= 56.25
Thus, the curved surface area of the sphere will increase by 56.25%.
Example: If the total surface area of a hemisphere is 462 cm2, then find its radius.
Solution: Let the radius of the hemisphere be r.
Total surface area of the hemisphere is given by the formula 3πr2.
It is given that the total surface area of the hemisphere is 462 cm2.
So, 462 cm2 = 3πr2
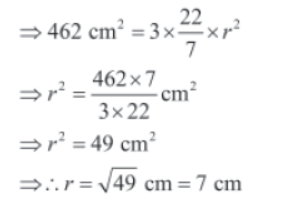
Thus, the radius of the hemisphere is 7 cm.
Example: A hemispherical steel bowl is 0.25 cm thick. The outer diameter of the bowl is 11 cm. Calculate the cost of tin-plating the inner surface of the bowl at the rate of Rs 16 per 100 cm2.
Solution: The figure according to the given specifications can be made as follows:

Outer diameter of the hemispherical bowl = 11 cm
∴ Outer radius of the hemispherical bowl = 11/2 cm = 5.5 cm
Thickness of the hemispherical bowl = 0.25 cm
∴ Inner radius (r) of the hemispherical bowl = (5.5 − 0.25) cm = 5.25 cm
Inner curved surface area of the hemispherical bowl = 2πr2
= (2 x 22/7 x 5.25 x 5.25) cm2
= (173.25 cm2
Cost of tin-plating 100 cm2 of surface = Rs 16
∴ Cost of tin-plating 1 cm2 of surface = Rs 16/100
⇒ Cost of tin-plating 173.25 cm2 of surface = Rs (173.25 x 16/100) = Rs 27.72 ≈ Rs 27.80
Thus, the cost of tin-plating the inner surface of the hemispherical bowl is Rs 27.80.
Example: A toy is in the shape of a right circular cylinder with a hemisphere at one end and a cone at the other. The height and radius of the cylindrical part are 13 cm and 5 cm respectively. Calculate the curved surface area of the toy if the height of the conical part is 12 cm.
Solution: The figure according to the given specifications can be made as follows:
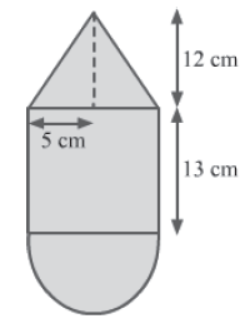
Radius (r) of the cylinder = 5 cm
Height (H) of the cylinder = 13 cm
Height (h) of cone = 12 cm
Radii of the cone and the hemisphere = Radius of the cylinder = 5 cm
Now, slant height (l) of the cone = √r2 +h2
= √52+122 cm
= √25+144 cm
= √169 cm
= 13 cm
∴ Surface area of the toy = CSA of the hemisphere + CSA of the cylinder + CSA of the cone
= 2πr2 + 2πrH + πrl
= πr(2r + 2H+l)
= 22/7 x 5 x (2 x 5 x 13 +13) cm2
= 22/7 x 5 x 49 cm2
= 770 cm2
Thus, the curved surface area of the toy is 770 cm2.
Example: Find the volumes of cubes of given sides.
(a) 2 cm (b) 5 m (c) 12 cm (d) 15 m
Solution: (a)
Measure of side of cube = 2 cm
Volume of cube = (Side)3 = 23 cm3 = 8 cm3
(b) Measure of side of cube = 5 m
Volume of cube = (Side)3 = 53 m3 = 125 m3
(c) Measure of side of cube = 12 cm
Volume of cube = (Side)3 = 123 cm3 = 1728 cm3
(d) Measure of side of cube = 15 m
Volume of cube = (Side)3 = 153 m3 = 3375 m3
Example 2: Find the volumes of cuboids of given dimensions.
(a) length = 5 cm, breadth = 2 cm, height = 6 cm
(b) length = 15 cm, breadth = 10 cm, height = 30 cm
(c) length = 1 m, breadth = 0.5 m, height = 1.5 m
Solution: (a)
We have
length = 5 cm, breadth = 2 cm, height = 6 cm
∴ Volume of cuboid = length × breadth × height
= (5 × 2 × 6) cm3
= 60 cm3
(b) We have
length = 15 cm, breadth = 10 cm, height = 30 cm
∴ Volume of cuboid = length × breadth × height
= (15 × 10 × 30) cm3
= 4500 cm3
(c) We have
length = 1 m, breadth = 0.5 m, height = 1.5 m
∴ Volume of cuboid = length × breadth × height
= (1 × 0.5 × 1.5) m3
= 0.75 m3
Example: If a cubical tank can contain 1331000 L of water, then find the edge of the tank.
Solution: Capacity of the cubical tank = 1331000 L
= 1331 m3 (∵ 1000 L = 1 m3)
Now, capacity of the tank = Volume of water that can be contained in the tank
We know that volume of water in the tank = (Edge)3
⇒ (Edge)3 = 1331 m3
⇒ ∴ Edge = 11 m
Thus, the edge of the cubical tank is 11 m.
Example : Find the height of the cuboid whose volume is 840 cm3and the area of whose base is 120 cm2.
Solution: Let the length, breadth and height of the cuboid be l, b and h respectively.
Area of the base of the cuboid = 120 cm2
∴ l × b = 120 cm2
Volume of the cuboid = 840 cm3
∴ l × b × h = 840 cm3
⇒ 120 cm2 × h = 840 cm3 (∵ l × b = 120 cm2)
⇒ h = 840/120 cm
⇒ ∴ h = 7 cm
Thus, the height of the cuboid is 7 cm.
Example : If the ratio of the edges of two cubes is 2 : 5, then find the ratio of their volumes.
Solution: Let the edges of the cubes be a = 2x and b = 5x.
Ratio of the volumes of the cubes = Volume of the first cube/Volume of the second cube
= a3/b3
= (2x)3/(5x)3
= 8x3/125x3
= 8/125
Thus, the volumes of the cubes are in the ratio 8 : 125.
Example : A solid cube of edge 18 cm is cut into eight cubes of equal volume. Find the dimension of each new cube. Also find the ratio of the total surface area of the bigger cube to that of the new cubes formed.
Solution: Let the edge of each new cube be x.
According to the question, we have:
Volumes of 8 cubes each of edge x = Volume of cube of edge 18 cm
⇒ 8 x x3 = (18 cm)3
⇒ x3 = 18 cm x 18cm x 18cm/8 = 729 cm3
⇒ x3 = (9 cm)3
⇒ ∴ x = 9 cm
Thus, the edge of each new cube is 9 cm.
Total surface area (S1) of the bigger cube = 6 × (18 cm)2
Total surface area of 8 cubes (S2) each of edge 9 cm = 8 × [6 × (9 cm)2]
∴ S1/S2 = 6 x 182/8 x 6 x 92 = 1/2
Hence, the required ratio is 1 : 2.
Example : A hostel having strength of 300 students requires on an average 36000 L of water per day. It has a tank measuring 10 m × 8 m × 9 m. For how many days will the water in the tank filled to capacity last?
Solution: Let the cuboidal tank have length l, breadth b and height h.
It is given that l = 10 m, b = 8 m and h = 9 m.
Capacity of the tank = l × b × h = 10 m × 8 m × 9 m = 720 m3
∴ Amount of water in the tank filled to capacity = 720 m3 = 720000 L (∵ 1000 L = 1 m3)
Amount of water used by 300 students in 1 day = 36000 L
Number of days for which the water in the full tank will
last = Amount of water in the full tank/Amount of water used in a day
= 720000/36000
= 20
Thus, the water in the tank filled to capacity will last for 20 days.
Example : The dimensions of a wall in a godown are 25 m × 0.3 m × 10 m. How many bricks of dimensions 25 cm × 10 cm × 5 cm were used to construct the wall?
Solution: Length (L) of the wall = 25 m = (25 × 100) cm = 2500 cm
Breadth (B) of the wall = 0.3 m = (0.3 × 100) cm = 30 cm
Height (H) of the wall = 10 m = (10 × 100) cm = 1000 cm
∴ Volume of the wall = L × B × H = (2500 × 30 × 1000) cm3
Length (l) of one brick = 25 cm
Breadth (b) of one brick = 10 cm
Height (h) of one brick = 5 cm
∴ Volume of one brick = l × b × h = (25 × 10 × 5) cm3
Number of bricks used to construct the wall = Volume of the wall/Volume of one brick
= 2500 x 30 x 1000/25 x 10 x 5
= 60000
Thus, 60000 bricks of dimensions 25 cm × 10 cm × 5 cm were used to construct the wall.
Example : A storeroom is in the form of a cuboid with dimensions 90 m × 150 m × 120 m. How many cubical boxes of edge 60 dm can be stored in the room?
Solution: Length (l) of the storeroom = 90 m
Breadth (b) of the storeroom = 150 m
Height (h) of the storeroom = 120 m
∴ Volume of the storeroom = l × b × h = (90 × 150 × 120) m3
Edge (a) of one cubical box = 60 dm = (60/10) m = 6 m
∴ Volume of one box = a3 = (6)3 m3
Number of boxes that can be stored in the room = Volume of the storeroom/Volume of one box
= 90 x 150 x 120/6 x 6 x 6
= 7500
Thus, 7500 cubical boxes of edge 60 dm can be stored in the room.
Example : A man-made canal is 5 m deep and 60 m wide. The water in the canal flows at the rate of 3 km/h. The canal empties its water into a reservoir. How much water will fall into the reservoir in 10 minutes?
Solution: Depth (h) of the canal = 5 m
Width (b) of the canal = 60 m
Length (l) of the canal is the rate of water flowing per hour = 3 km = 3000 m
Amount of water flowing per hour = l × b × h = (3000 × 60 × 5) m3 = 900000 m3 = 900000
kL (∵ 1 m3 = 1 kL)
∴ Amount of water flowing in 60 min = 900000 kL
⇒ Amount of water flowing in 1 minute = (900000/60)KL
⇒ Amount of water flowing in 10 minutes = (900000/60 X 10) KL
= 150000 kL
Thus, 150000 kL of water will fall into the reservoir in 10 minutes.
Example : The external length, breadth and height of a closed rectangular wooden box are 9 cm, 5 cm and 3 cm respectively. The thickness of the wood used is 0.25 cm. The box weighs 7.5 kg when empty and 50 kg when it is filled with sand. Find the weights of one cubic cm of wood and one cubic cm of sand.
Solution: External length (L) of the wooden box = 9 cm
External breadth (B) of the wooden box = 5 cm
External height (H) of the wooden box = 3 cm
∴ External volume of the wooden box = L × B × H = (9 × 5 × 3) cm3 = 135 cm3
Thickness of the wood used = 0.25 cm
Internal length (l) of the wooden box = 9 cm − (0.25 cm + 0.25 cm) = 8.5 cm
Internal breadth (b) of the wooden box = 5 cm − (0.25 cm + 0.25 cm) = 4.5 cm
Internal height (h) of the wooden box = 3 cm − (0.25 cm + 0.25 cm) = 2.5 cm
∴ Internal volume of the wooden box = l × b × h = (8.5 × 4.5 × 2.5) cm3 = 95.625 cm3
Now, volume of the wood = External volume of the box − Internal volume of the box
= (135 − 95.625) cm3
= 39.375 cm3
Weight of the empty box = 7.5 kg
⇒ Weight 39.375 cm3 of wood = 7.5 kg
∴ Weight of 1 cm3 of wood = (7.5/39.375) kg = 0.19 kg
Now, volume of sand = Internal volume of the box = 95.625 cm3
Weight of sand = Weight of the box filled with sand − Weight of the empty box
= (50 − 7.5) Kg
= 42.5 Kg
⇒ Weight of 95.625 cm3 of sand = 42.5 kg
∴ Weight of 1 cm3 of sand = (42.5/95.625) kg = 0.44 kg
Example : A cylindrical tank can hold 11000 L of water. What is the radius of the base of the tank if its height is 3.5 m?
Solution: Let r be the radius of the base of the cylindrical tank.
Height (h) of the tank = 3.5 m
Volume of the tank = 11000 L = 11 m3 (∵ 1000 L = 1 m3)
Volume of a cylinder = πr2h
In this case, we have
πr2h = 11 m3
⇒ (22/7 x r2 x 3.5 m) = 11 m2
⇒ 11 r2 = 11 m2
⇒ r = 1 m
Thus, the radius of the base of the cylindrical tank is 1 m.
Example : What is the height of a cylinder whose volume is 6.16 m3 and the diameter of whose base is 28 dm?
Solution: Diameter of the base of the cylinder = 28 dm
∴ Radius (r) of the base = (28/2) dm
= 14 dm
= (14/10) m (∴ 1 dm = 1/10 m)
= 1.4 m
Volume of the cylinder = 6.16 m3
⇒ πr2h = 6.16 m3
⇒ 22/7 x (1.4 m)2 x h x 6.16 m3
⇒ h = [6.16 x 7/22 x (1.4)2]m
⇒ h = 1 m
Thus, the height of the cylinder is 1 m.
Example : The external diameter, thickness and length of a cylindrical water pipe are 22 cm, 1 cm, and 8 m respectively. What amount of material went into making this pipe?
Solution: External diameter of the hollow cylindrical pipe = 22 cm
∴ External radius, R = (22/7) cm = 11 cm
Thickness of the pipe = 1 cm
∴ Internal radius, r = (11 − 1) cm = 10 cm
Length (h) of the pipe = 8 m = (8 × 100) cm = 800 cm (∵ 1 m = 100 cm) = π(R2 – r2) h
= [22/7 x (112 – 102) x 800] cm
= [22/7 x 21 x 800] cm3
= 52800 cm3
Thus, 52800 cm3 of material was used to make the water pipe.
Example : The diameter and height of a solid metallic cylinder are 21 cm and 25 cm respectively. If the mass of the metal is 8 g per cm3, then find the mass of the cylinder.
Solution: Diameter of the cylinder = 21 cm
∴ Radius (r) of cylinder = (21/2) cm
Height (h) of the cylinder = 25 cm
To find the mass of the metallic cylinder, we have to first find the volume of the cylinder.
Volume of the cylinder = πr2h
= [22/7 x (21/2) x (21/2) x 25 ] cm3
= 8662.5 cm3
Mass of 1 cm3 of the metal = 8 g
∴ Mass of 8662.5 cm3 of the metal= (8662.5 × 8) g
= 69300 g
= (69300/1000) kg (∴ 1 g = 1/1000 kg)
= 69.3 kg
Thus, the mass of the cylinder is 69.3 kg.
Example : A rectangular sheet of paper is folded to form a cylinder of height 12 cm. If the length and breadth of the sheet are 44 cm and 12 cm respectively, then find the volume of the cylinder.
Solution: Height (h) of the cylinder = 12 cm
Let r be the radius of the cylinder. We can find this value from the circumference of the base of the cylinder. As shown in the figure, this circumference is nothing but the length of the sheet.
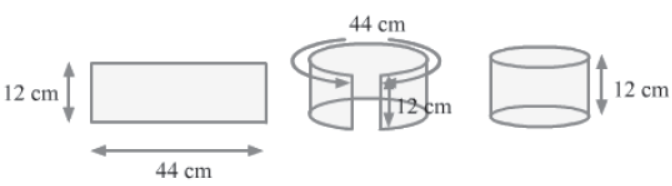
So, circumference of the base of the cylinder = 44 cm
⇒ 2πr = 44
⇒ r = 44/2π
⇒ r = 44 x 7/2x 22
⇒ r = 7 cm
Now, volume of the cylinder = πr2h
= 22/7 x 7 x 7 x 12 cm3
= 1848 cm3
Example : The inner and outer diameters of a cylindrical iron pipe are 54 cm and 58 cm respectively and its length is 5 m. What is the mass of the pipe if 1 cm3 of iron has a mass of 8 g?
Solution: Inner diameter of the hollow cylindrical iron pipe = 54 cm
∴ Inner radius, r = (54/2) cm = 27cm
Outer diameter of the pipe = 58 cm
∴ Outer radius, R = (58/2) cm = 29 cm
Length (h) of the pipe = 5 m = (5 × 100) cm = 500 cm
∴ Volume of the pipe = π(R2 – r2) h
= [22/7 x (292 – 272) x 500]cm3
= [22/7 x 112 x 500] cm3
= 176000 cm3
Mass of 1 cm3 of iron = 8 g
∴ Mass of 176000 cm3 of iron = (8 × 176000) g
= (8 x 176000/1000)kg (∴ 1 g = 1/1000 kg)
= 1408 kg
Thus, the mass of the hollow cylindrical iron pipe is 1408 kg.
Example : The internal and external radii of a cylindrical juice can (as shown in the figure) are 3.5 cm and 4.2 cm respectively. The total height of the can is 7.7 cm. The thickness of the base (i.e., a solid cylinder) is 0.7 cm. If the mass of the material used in the can is 3 g per cm3, then find the mass of the can.
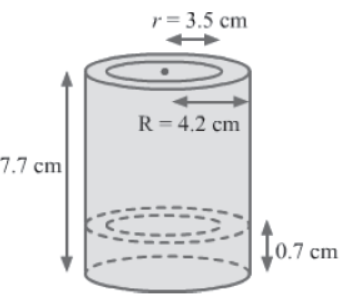
Solution: To find the mass of the juice can, we need to first find its volume.
The juice can shown in the figure contains two cylinders. One is a solid cylinder (i.e., the base of the can) and the other is a hollow cylinder (i.e., the cylindrical part that stands on the base).
External radius (R) of the hollow cylinder = 4.2 cm
Internal radius (r) of the hollow cylinder = 3.5 cm
Thickness (h) of the base = 0.7 cm (i.e., the height of the solid cylinder)
Total height (H) of the juice can = 7.7 cm
∴ Height (h’) of the hollow cylinder = (7.7 − 0.7) cm = 7 cm
Volume of the juice can = Volume of the solid base + Volume of the hollow cylinder on the base

Mass of the material per cm3 = 3 g
∴ Mass of the material used in the container = (3 × 157.388) g
= 472.164 g
Thus, the mass of the juice can is 472.164 g.
Example : A well 3.5 m in diameter and 20 m deep is dug in a rectangular field of dimensions 20 m × 14 m. The earth taken out is spread evenly across the field. Find the level of earth raised in the field.
Solution:
Length (l) of the field = 20 m
Breadth (b) of the field = 14 m
Diameter (d) of the well = 3.5 m
∴ Radius (r) of the well= 3.5/2 m
Depth (h) of the well = 20 m
Volume of the dug out earth = πr2h
Now, the area of the field on which the dug out earth is spread is given by the difference between the area of the entire field and the area of the field covered by the cross-section of the well.
⇒ l × b − πr2
Let H be the level of earth raised in the field.
Volume of earth spread in the field = Volume of the dug out earth
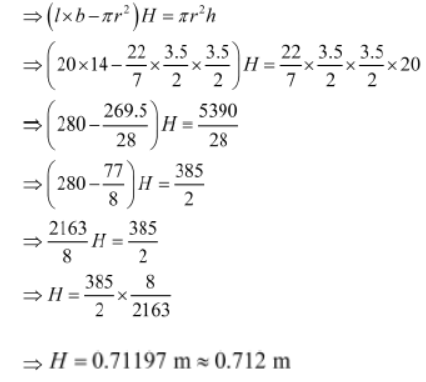
Therefore, the level of earth in the field is raised by about 0.712 m.
Example : The height and slant height of a conical funnel are 21 cm and 29 cm respectively. How many litres of water can the funnel hold?
Solution:
The amount of water that the funnel can hold is equal to the volume of the funnel.
Height (h) of the funnel = 21 cm
Slant height (l) of the funnel= 29 cm
Let the radius of the circular base of the funnel be r.
Now, l2 = r2 + h2
⇒ (29 cm)2 = r2 + (21 cm)2
⇒ 841 cm2 = r2 + 441 cm2
⇒ r2 = (841 − 441) cm2
⇒ r2 = 400 cm2
⇒ r = √400 cm = 20 cm
Volume of the funnel – 1/3 πr2h
= (1/3 x 22/7 x 20 x 20 x 21) cm3
= 8800 cm3
= 8800/1000 L (∴ 1 cm3 = 1/1000/ L)
= 8.8 L
Thus, the funnel can hold 8.8 L of water.
Example : If A, B and C are respectively the height, volume and curved surface area of a cone, then prove that 3B (πA3 + 3B) = C2A2.
Solution: It is given that A, B and C are respectively the height, volume and curved surface area of the cone.
Let r and l be the radius and slant height of the cone.
Now,
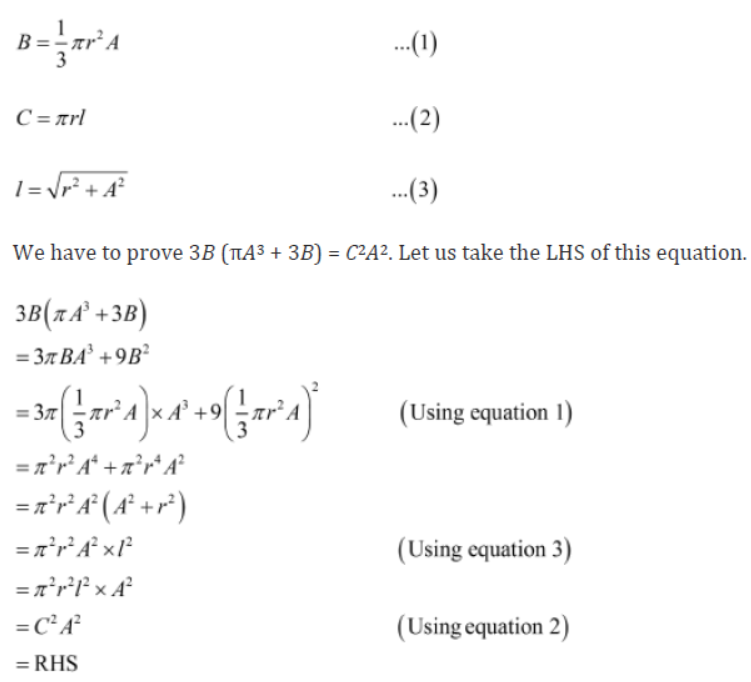
Example : The radius and slant height of a cone are in the ratio 3 : 5. If the volume of the cone is 12936 m3, then find the radius, height and slant height of the cone.
Solution: Let the radius (r) and slant height (l) of the cone be 3x and 5x respectively.
Let the height of the cone be h.
We know that l2 = r2 + h2
⇒ (5x)2 = (3x)2 + h2
⇒ h2 = 25×2 − 9×2
⇒ h2 = 16×2
⇒ h = √16 x2 = 4x
Volume of a cone = 1/3 πr2h
It is given that the volume of the cone is 12936 m3.
So, 1/3 πr2h = 1293 m3
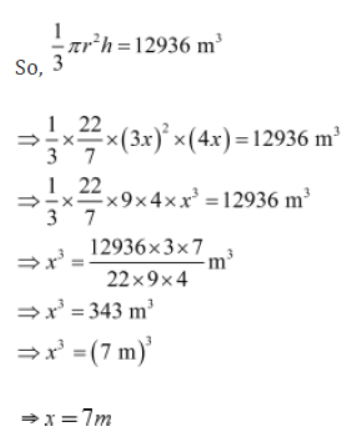
Now, r = 3x = (3 × 7) m = 21 m
h = 4x = (4 × 7) m = 28 m
l = 5x = (5 × 7) m = 35 m
Thus, the radius, height and slant height of the cone are 21 m, 28 m and 35 m respectively.
Example : If the radii and heights of two cones are in the ratios 2 : 3 and 5 : 4 respectively, then find the ratio of the volumes of the cones.
Solution: Let r1 and h1 be the radius and height of one cone.
Let r2 and h2 be the radius and height of the other cone.
It is given that the radii of the cones are in the ratio 2 : 3.
∴ r1/r2 = 2/3
It is given that the heights of the cones are in the ratio 5 : 4.
∴ h1/h2 = 5/4
Ratio of the volumes of the cones = Volume of the cone/Volume of the second cone
= 1/3 πr21 h1/1/3 πr22 h2
= (r1/r2)2 x (h1/h2)
= (2/3)2 x (5/4)
= 4/9 x 5/4
= 5/9
Thus, the volumes of the two cones are in the ratio 5 : 9.
Example : Find the radius of a sphere if its volume is 179,2/3 cm3
Solution: Volume of a sphere = 4/3 πr3
It is given that the volume of the given sphere is 179,2/3 cm3
Let the radius of the given sphere be r.
So,
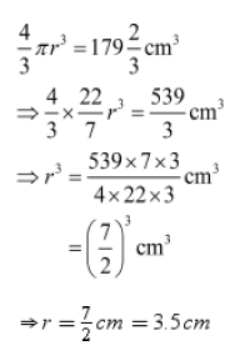
Thus, the radius of the sphere is 3.5 cm.
Example : Find the volume of a sphere if its surface area is 154 cm2.
Solution: Surface area of a sphere = 4πr2
It is given that the surface area of the given sphere is 154 cm2.
Let the radius of the given sphere be r.
So, 4πr2 = 154
⇒ 4 x 22/7 x r2 = 154
⇒ r2 = 154×7/22 x 4
⇒ r2 =49/4
⇒ r = 7/2 cm
Now, volume of a sphere = 4/3πr3
Therefore, volume of the given sphere = 4/3 x 22/7 x 7/2 x 7/2 x 7/2 cm3
= 179.67 cm3
Example : The diameter of Earth is about 20/19 times that of Venus. What is the ratio of their volumes?
Solution: Volume of a sphere = 4/3πr3
Let the diameter of Venus be x.
∴ Diameter of Earth = 20/19 x
Now, radius (r1) of Venus = x/2
And, radius (r2) of Earth = 10/19 x
Ratio of the volumes of the two planets = Volume of Earth/Volume of Venus
= 4/3πr23/3/4πr13
= (r1/r2)3
= (10/19x/x/2)3
= (20/19)3
= 8000/6859
Thus, the ratio of the volumes of Earth and Venus is 8000 : 6859.
Example : How many litres of milk can a hemispherical bowl of diameter 21 cm hold?
Solution: Diameter of the hemispherical bowl = 21 cm
∴ Radius (r) of the hemispherical bowl= 21/2 cm
Volume of the hemispherical bowl = 2/3πr3
= 2/3 x 22/7 x 21/2 x 21/2 x 21/2 cm3
= 2425.5 cm3
= 2425.5/1000 L (∴ 1 cm3 = 1/1000 L)
= 2.4255 L
≈ 2.43 L
Thus, the hemispherical bowl can hold approximately 2.43 L of milk.
Example 1: A hemispherical bowl is made of one-centimetre-thick steel. The inside radius of the bowl is 6 cm. Find the volume of steel used in making the bowl.
Solution:
Inner radius (r) of the hemispherical bowl = 6 cm
Outer radius (R) of the bowl = (6 + 1) cm = 7 cm (∵ Steel used has thickness of 1 cm)
Volume of the inner hemisphere = 2/3 πr3
Volume of the outer hemisphere = 2/3 πR3
∴ Volume of steel used = 2/3 π(R3 – π3)
= 2/3 X 22/7 X [(7)3 – (6)3] cm3
= 2/3 x 22/7 x (343 – 216) cm3
= 2/3 x 22/7 x 127 cm3
= 266.095 cm3
Thus, the volume of steel used in making the bowl is 266.095 cm3.
Example : A solid is in the form of a cylinder with hemispherical ends as is shown in the figure. Find the volume of the solid.
Solution:
It is given that:
Radius (r) of the cylinderical part of the solid = 7 cm
Height (h) of the same = [41 − (2 × 7)] cm = (41 − 14) cm = 27 cm
Also, radius of each hemispherical part is the same as that of the cylinderical part.
∴ Volume of the solid = Volume of the cylinderical part + Volumes of the hemispherical parts
= πr2 h + 2(2/3πr3)
= πr2(h+4r/3)
= 22/7 x 7 x 7x(27+4×7/3)cm3
= 22/7 x 7 x 7x 109/3 cm3
= 5595.33 cm3
Example : Find the number of spherical lead shots each 2.1 cm in diameter which can be obtained from a rectangular solid of lead with dimensions 66 cm × 42 cm × 21 cm.
Solution: Let x number of spherical lead shots be obtained from the given solid of lead.
Volume of a cuboid = l × b × h
∴ Volume of lead in the given rectangular solid = (66 × 42 × 21) cm3
Diameter of a lead shot = 2.1 cm
∴ Radius of a lead shot =2.1/2 cm = 1.05 cm
Volume of a sphere = 4/3πr3
∴Volume of a lead shot = 4/3 x 22/7 x (1.05)3 cm3
⇒ Volume of x number of lead shots = 4/3 x 22/7 xx x (1.05)3 cm3
According to the question, we have:
Volume of x number of lead shots = Volume of lead in the rectangular solid
So,
4/3 x 22/7 xx x (1.05)3 = 66 x 42 x 21
⇒ x = 66 x 42 x 21 x 3 x 7/4 x 22 x (1.05)3
⇒ x = 12000
Thus, 12000 spherical lead shots can be formed from the given solid of lead.
Example : Find the volume (in terms of π) of the solid figure obtained when a right triangle with sides 8 cm, 15 cm and 17 cm is revolved about the side
i) 8 cm.
ii) 15 cm.
Solution: i) The sides of the given right triangle are 8 cm, 15 cm and 17 cm.
If this right triangle is revolved about the side 8 cm, then we will obtain a solid figure as is shown.
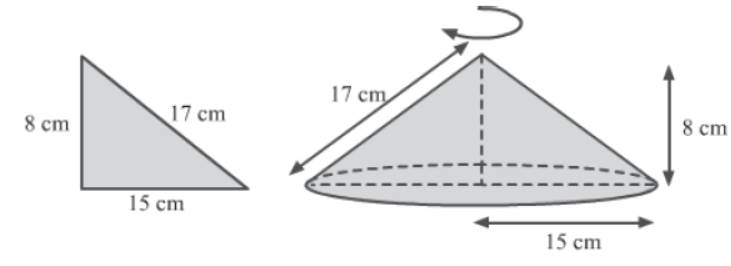
The solid figure so obtained is a cone.
The radius (r)and height (h) of the cone are 15 cm and 8 cm respectively.
∴ Volume of the cone formed 1/3 πr2h
= 1/3 x π x 15 x 15 x 8 cm3
= 600 π cm3
ii) If the same right triangle is revolved about the side 15 cm, then we will obtain the following solid figure.

Again, the solid figure so obtained is a cone.
The radius (r)and height (h) of the cone are 8 cm and 15 cm respectively.
∴ Volume of the cone formed = 1/3 πr2h
= 1/3 x π x 8 x 8 x 15 cm3
= 320 π cm3
Example: The surface area of a sphere of radius 5 cm is five times the curved surface area of a cone of radius 4 cm. Find the
i) height of the cone.
ii) volume of the cone.
Solution:
i) Let r1 be the radius of the sphere and r2 be the radius of the cone.
Let h the height and l the slant height of the cone.
It is given that r1 = 5 cm and r2 = 4 cm
According to the question, we have:
Surface area of the sphere = 5 × Curved surface area of the cone

Thus, the height of the cone is 3 cm.
ii) Volume of the cone = 1/3πr22h
= 1/3 x 22/7 x 4 x 4 x 3 cm3
= 50.29 cm3


