Linear Inequalities Class 11 Mathematics Important Questions

Please refer to Linear Inequalities Class 11 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 11 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 11 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 11.

Class 11 Mathematics Important Questions Linear Inequalities

Assertion & Reasoning Based MCQs

(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.

Question. Assertion : If –5 ≤ 2x + 9 ≤ 2, then x ∈ [–7, –3.5].
Reason : The graphical representation of –5 ≤ 2x + 9 ≤ 2 is

Question. Assertion : |3x – 5| > 9 ⇒ x∈ (-∞ , 4/3) ∪ (14/3 ,∞) .
Reason : The region containing all the solutions of an inequality is called the solution region.

Question. Assertion : If x ≥ – 3, then x + 5 ≥ 2.
Reason : Same number can be added to both sides of the inequality without changing the sign of inequality.

Question. Assertion : If 11x – 9 ≤ 68, then x ∈ (–∞, 7).
Reason : If an inequality consist of signs ≤ or ≥, then the point on the line are also included in the solution region.

Question. Assertion : If a < b, c < 0, then a/c < b/c .
Reason : If both sides are divided by the same negative quantity, then the inequality is reversed.

Very Short Answer Type Questions :

Question. Solve 5x – 2 < 3x + 1 when x is real.
Answer: We have, 5x –2 < 3x + 1 ⇒ 2x < 3 ⇒ x < 3/2
∴ x ∈ (–∞, 3/2)

Question. Solve : –8 ≤ 5x – 3 < 7 where x ∈ Z.
Answer: We have, –8 ≤ 5x – 3 < 7
⇒ –8 ≤ 5x – 3 and 5x – 3 < 7
⇒ 5x ≥ –5 and 5x < 10
⇒ x ≥ –1 and x < 2
∴ –1 ≤ x < 2
Also, x ∈ Z. So, x = {–1, 0, 1}

Question. Solve the linear inequation : 2x – 6 ≤ 0
Answer: We have, 2x – 6 ≤ 0 ⇒ 2x ≤ 6 ⇒ x ≤ 3
Hence, any real number less than or equal to 3 is a solution of the given inequation.
The solution set of the given inequation is (–∞, 3]

Question. Solve the following inequation for x, where x is a natural number : 5x – 2 < 3x +3
Answer: We have,
5x – 2 < 3x + 3 ⇒ 2x < 5 ⇒ x < 5/2 Since, x ∈ N. So, x = {1, 2}

Question. Solve the linear inequation : 4x – 20 ≥ 0
Answer: We have, 4x –20 ≥ 0 ⇒ 4x ≥ 20 ⇒ x ≥ 5
Hence, the solution set of the given inequation is [5, ∞).

Question. Solve : 30x < 200, when x is a natural number.
Answer: We have, 30x < 200
⇒ x < 20/3 , as x ∈ N
∴ x = {1, 2, 3, 4, 5, 6}

Question. Solve 14x > 72 where x is natural number.
Answer: We have, 14x >72 ⇒ x > 5 , 1/7
Since, x ∈ N. So, x = {6, 7, ……}

Question. Solve the linear inequation : 7x + 9 > 37
Answer: We have, 7x + 9 > 37 ⇒ 7x > 37 – 9
⇒ 7x > 28 ⇒ x > 4
Hence, (4, ∞) is the solution set of the given inequation.

Question. Solve the inequation : 3x – 10 > 5x + 1
Answer: Given inequation is 3x –10 > 5x + 1
⇒ 3x – 5x > 1+ 10 ⇒ –2x > 11⇒ x < − 11/2 
Hence, the solution set of the given inequation is
{x ∈ R : x < -11/2} ; the set (-∞ , -11/2) .

Question. Solve the linear inequation : –3x + 15 < 0
Answer: We have, –3x + 15 < 0 ⇒ –3x < –15 ⇒ x > 5
Thus, any real number greater than 5 is a solution of the given inequation.
∴ x ∈ (5, ∞)

Short Answer Type Questions :

Question. Solve the inequality x/3 – x-2/4 > x-1/5 , where x belongs to R.
Answer: We have, x/3 – x-2/4 > x-1/5
⇒ 4x-3x + 6/12 > x-1/5
⇒ x+6/12 > x-1/5
⇒ 5x + 30 > 12x − 12 ⇒ 7x < 42 ⇒ x < 6
∴ x ∈ (–∞, 6)

Question. Solve the inequality : x+8/x-2 ≥ 0 .
Answer: x+8/x-2 ≥ 0 , can be written as
x+8/x-2 x (x-2)2 ≥ 0 x (x-2)2 ⇒ (x+8) (x-2) ≥ 0
Product of two factors (x + 8) and (x – 2) will be positive :
Case I : If both are positive, i.e., (x + 8) ≥ 0 and (x – 2) > 0, i.e., x ≥ –8 and x > 2 ⇒ x > 2 ⇒ x ∈(2, ∞)
Case II : If both are negative, i.e., (x + 8) ≤ 0 and (x – 2) < 0, i.e., x ≤ –8 and x < 2 ⇒ x ≤ –8 ⇒ x ∈(–∞, –8]
Thus, the solution is (–∞, –8] ∪ (2, ∞)

Question. Solve the inequation x+3/x-2 ≥ 4 .
Answer: We have, x+3/x-2 ≥ 4 , x ≠ 2
⇒ x+3/x-2 – 4 ≥ 0 ⇒ x+3-4x+8/x-2 ≥ 0
⇒ -3x+11/x-2 ≥ 0 ⇒ -(3x-11)/x-2 ≥ 0
⇒ 3x+11/x-2 ≤ 0 ⇒ 2 < x ≤ 11/3
Thus, the solution set of given inequation is (2,11/3]

Question. In drilling a hole, x km below the surface of the earth it was found that the temperature T in degree Celsius was given by T = 30° + 25°(x – 3), 3 < x < 15. At what depth will the temperature be between 200°C and 300°C?
Answer: We have, T = 30° + 25°(x –3), 3 < x < 15
Now 200° < 30° + 25°(x– 3) < 300°
⇒ 170° < 25°(x – 3) < 270°
⇒ 170°/25° < (x – 3) < 270°/25°
⇒ 6.8 < (x – 3) < 10.8
⇒ 6.8 + 3 < x < 10.8 + 3
⇒ 9.8 < x < 13.8
Thus required depth will be between 9.8 km and 13.8 km.

Question. Solve the linear inequality 
x/4 > 5x-2/3 – 7x-3/5 , x ∈ R.
Answer: We have, x/4 > 5x-2/3 – 7x-3/5 
⇒ x/4 > 25x – 10 – 21x + 9/15
⇒ x/4 > 4x-1/15 ⇒ 15x > 16x − 4 ⇒ x < 4
∴ x ∈ (–∞, 4)

Question. Solve the inequality for real x.
(2x-1)/3 ≥ (3x-2)/4 – (2-x)/5
Answer: We have, 2x-1/3 ≥ 3x-2/4 – 2-x/5
⇒ 2x-1/3 ≥ 15x – 10 – 8+4x/20
⇒ 40x − 20 ≥ 57x − 54
⇒ 34 ≥ 17x ⇒ x ≤ 2
∴ x ∈ (–∞, 2]

Question. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
Answer: Let x be the smaller of two positive consecutive even
integers, then the other one is x + 2.
We have, x > 5 and x + x + 2 < 23 ⇒ 2x + 2 < 23
⇒ 2x < 21 ⇒ x < 21/2
∴ x can be 6, 8, 10 ( x > 5 and numbers are even integers)
∴ The pairs are [(6, 8), (8, 10), (10, 12)]

Question. Solve and represent the solution on number line :
3x+1/4 – x-2/3 > 1/12 , 2x-3/4 + 6 ≤ 2+4x/3 .
Answer: We have, 3x+1/4 – x-2/3 > 1/12
⇒ 9x + 3 – 4x + 8 > 1
⇒ 5x + 11 > 1 ⇒ 5x > –10 ⇒ x > –2
Also, 2x-3/4 + 6 ≤ 2+4x/3 
⇒ 2x-3+24/4 ≤ 6+4x/3
⇒ 2x+21/4 ≤ 6+4x/3
⇒ 6x + 63 ≤ 24 + 16x
⇒ 10x ≥ 39 ⇒ x ≥ 3.9 …
The solution is represented on number line as follows :

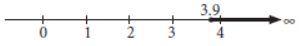
Question. Solve the following system of inequalities graphically : y ≤ 4x + 1, y – 2x ≥ 1, x ≤ 3, x ≥ 0, y ≥ 0.
Answer: Converting the given inequations into equations, we get
y = 4x + 1 …(i) y – 2x = 1 …(ii)
x = 3 …(iii) x = 0, y = 0 …(iv)
Now, we draw the graphs of (i), (ii), (iii) and (iv) as shown below.

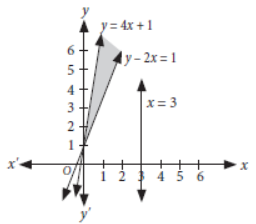
So, the shaded region represents the solution set of given system of linear inequalities.

Question. Solve for the real x :
4+2X/3 ≥ X/2 -3
Answer: We have, 4+2x/3 ≥ x/2 -3
⇒ 4+2x /3 ≥ x-6/2
⇒ 8 + 4x ≥ 3x –18 ⇒ x ≥ –26
∴ x ∈[–26, ∞)

Question. Solve the following system of inequations :
5x/4 + 3x/8 > 39/8 , 2x-1/12 – x-1/3 < 3x+1/4
Answer: The given system of inequation is

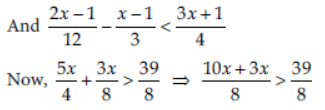
⇒ 13x > 39 ⇒ x > 3
⇒ x ∈(3, ∞)
So, the solution set of inequation (i) is the interval (3, ∞).

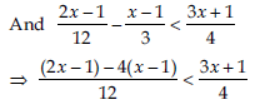
⇒ –2x + 3 < 3(3x + 1)
⇒ –2x + 3 < 9x + 3 ⇒ –2x – 9x < 3 – 3
⇒ –11x < 0 ⇒ x > 0 ⇒ x ∈(0, ∞)
So, the solution set of inequation (ii) is the interval (0, ∞).
We observe that the intersection of the solution sets of inequations (i) and (ii) is interval (3, ∞).

Question. A person was not feeling well, so he went to a doctor. Doctor on examination found that his temperature varies between 30°C to 35°C. What is the range of temperature for body in Fahrenheit?
Use conversion formula F = 9/5 C + 32°
Answer: We are given that,
30° < C < 35°
⇒ 9/5 x 30° < 9/5 C < 9/5 x 35° ⇒ 54° < 9/5 C < 63°
⇒ 54° + 32° < 9/5 C + 32°< 63° + 32°
⇒ 86° < 9/5C +32°<95° ⇒ 86° < F < 95°

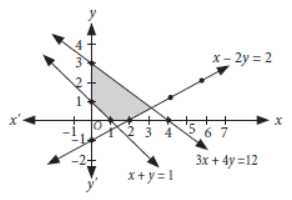
Question. Solve the following system of linear inequalities graphically :
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Answer: Converting the inequations into equations, we get
x – 2y = 3 …(i)
3x + 4y = 12 …(ii)
y = 1 …(iii)
x = 0 …(iv)
Now, draw the graphs of (i), (ii) (iii) and (iv) as shown below.

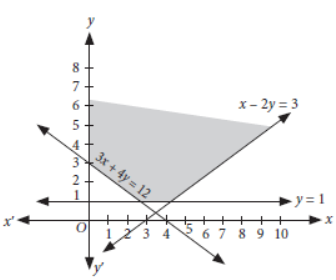
So, the shaded region represents the solution set of given system of linear inequalities.

Question. Solve : 5-2x/3 ≤ x/6 – 5
Answer: We have, 5-2x/3 ≤ x/6 -5
⇒ 5-2x/3 ≤ x-30/6
⇒ 10 – 4x ≤ x – 30 ⇒ 40 ≤ 5x ⇒ 8 ≤ x ⇒ x ≥ 8

Question. Solve the system of inequations :
x/2x+1 ≥ 1/4 , 6x/4x-1 < 1/2
Answer: We have, x/2x+1 ≥ 1/4
And 6x/4x-1 < 1/2 25
⇒ x ∈(–1/8, 1/4) …(iv)
We can see that the intersection of (iii) and (iv) is the null set. Hence, the given system of inequations has no solution.

Question. Solve and represent the solution graphically on number line :
3x – 7 > 2(x – 6), 6 – x > 11 – 2x
Answer: We have, 3x – 7 > 2(x – 6) and 6 – x > 11 – 2x
⇒ 3x – 7 > 2x – 12 and x > 5
⇒ x > –5 and x > 5
So, the solution set is (5, ∞).
The solution on the number line is as shown below :

Question. Solve the following system of inequalities graphically :
5x + 4y ≤ 40, x ≥ 2, y ≥ 3.
Answer: Converting the given inequations into equations,
we get
5x + 4y = 40 …(i)
x = 2 …(ii)
y = 3 …(iii)
Now, draw the graphs of (i), (ii) and (iii) as shown below.

So, the shaded region including all the points on the lines represents the solution set of the given system of inequalities.

Question. Solve the following system of linear inequalities graphically :
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x ≥ 0, y ≥ 0.
Answer: Converting the given inequations into equations,
we get
4x + 3y = 60 …(i)
y = 2x …(ii)
x = 3 …(iii)
x = 0, y = 0 …(iv)
Now, we draw the graphs of (i), (ii), (iii) and (iv) as shown below.

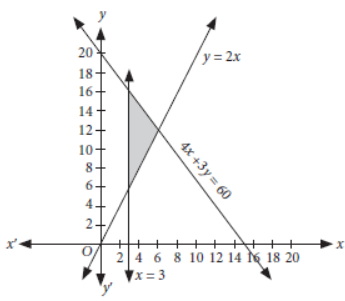
So, the shaded region including all the points on the lines represents the solution set of the given system of linear inequalities.

Question. Solve the inequality x-1/x+1 ≥ 0 and represent the solution set on the number line.
Answer: Given inequality is x-1/x+1 ≥ 0
First of all we note that x + 1 ≠ 0
Case I : If x + 1 > 0, i.e., if x > –1, then
(i) ⇒ x – 1 ≥ 0, i.e., x ≥ 1
So [1, ∞) is a subset of the solution set.
Case II : If x + 1 < 0, i.e., if x < –1, then
(i) ⇒ x – 1 ≤ 0, i.e., x ≤ 1; but x < –1,
So (–∞, –1) is also a subset of the solution set.
Thus, the solution set of the given inequality is
(–∞, –1) ∪ [1, ∞) which can be represented on the number line as shown below.

Question. The cost and revenue functions of a product are given by C(x) = 2x + 400 and R(x)= 6x + 20 respectively, where x is the number of items produced by the manufacturer. How many items the manufacturer must sell to realize some profit?
Answer: We know that, Profit = Revenue – Cost
Therefore, to earn some profit we must have Revenue > Cost
⇒ 6x + 20 > 2x + 400 ⇒ 6x – 2x > 400 – 20
⇒ 4x > 380
⇒ x > 380/4 ⇒ x > 95
Hence, the manufacturer must sell more than 95 items to realize some profit.

Question. Solve : 5(2x – 7) – 3(2x + 3) ≤ 0 and 2x + 19 ≤ 6x + 47 and represent the solution on number line.
Answer: Consider the inequation
5(2x – 7) – 3(2x + 3) ≤ 0
⇒ 10x – 35 – 6x – 9 ≤ 0
⇒ 4x ≤ 44 ⇒ x ≤ 11 …(i)
Consider the inequation,
2x + 19 ≤ 6x + 47
⇒ 19 – 47 ≤ 6x – 2x
⇒ –28 ≤ 4x ⇒ –7 ≤ x
⇒ x ≥ –7 …(ii)
From (i) and (ii), we get –7 ≤ x ≤ 11, which can be represented on the number line as shown below.

Question. Solve the following system of inequation 5x – 7< 3(x+3) , 1-3x/2 ≤ x – 4 .
Answer: We have, 5x – 7< 3(x+3) , 1-3x/2 ≤ x – 4
⇒ 5x – 3x < 9 + 7 and 2 – 3x ≤ 2x – 8
⇒ 2x < 16 and –5x ≤ –10
⇒ x < 8 and x ≥ 2
⇒ 2 ≤ x < 8.

Question. Solve the following system of inequalities graphically :
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, x – y ≥ 1
Answer: Converting the given inequations into equations, we get
x – 2y = 3 …(i)
3x + 4y = 12 …(ii)
x – y = 1 …(iii)
x = 0 …(iv)
Now, we draw the graphs of (i), (ii), (iii) and (iv) as shown below.

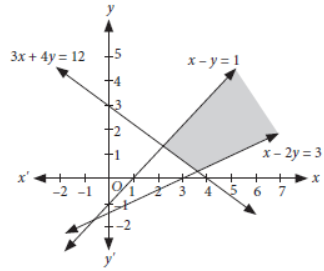
So, the shaded region including all the points on the lines represents the solution set of the given system of linear inequalities.

Question. Solve the following system of inequations graphically :
x – 2y ≤ 0, 2x – y + 2 ≥ 0, x ≥ 0, y ≥ 0
Answer: Converting the given inequations into equations, we get
x – 2y = 0 …(i)
2x – y + 2 = 0 ⇒ 2x – y = –2 …(ii)
x = 0, y = 0 …(iii)
Now, draw the graphs of (i), (ii) and (iii), as shown below.

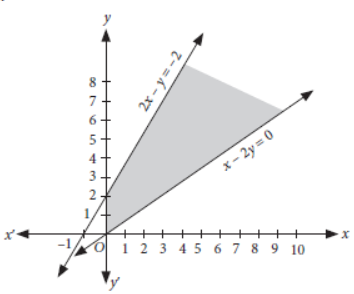
So, the shaded region represents the solution set of given system of linear inequalities.

Question. Solve the inequalities x/2 < (5x-2)/3 – (7x-3)/5 and show the graph of the solution on number line.
Answer: We have, x/2 < (5x-2)/3 – (7x-3)/5
⇒ x/2 < 25x-10-21x + 9/15
⇒ 15x < 2(4x – 1) ⇒ 15x < 8x – 2
⇒ 7x < – 2 ⇒ x < -2/7
∴ Solution set is (-∞ , -2/7) , i.e.,

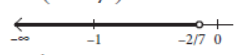
Long Answer Type Questions :

Question. A milkman has 80% milk in his stock of 800 litres of adulterated milk. How much 100% pure milk is to be added to it so that purity is between 90% and 95%. How much pure milk he should add to his stock to obtain 99% pure milk? What should be done to stop adulteration in foods?
Answer: Let x litres of 100% pure milk be added so that we get purity between 90% and 95%. We have to given that 80% of milk of stock is adulterated milk. It mean’s that there is 20% or 200 litre pure milk is available in his stock. Hence total mixture is 1000 litres.
∴ 1000 x 90/100 ≤ 800 + x ≤ 95 x 1000/100
⇒ 900 ≤ 800 + x and 800 + x ≤ 950
⇒ 100 ≤ x and x ≤ 150
Hence for getting 90% and 95% pure milk we must add 100 and 150 litres of pure milk.
For 99% pure milk
800 + x ≥ 99 x 1000/100
⇒ 800 + x ≥ 990 ⇒ x ≥ 190 litres
∴ 190 litres pure milk must be added for getting 99% pure milk.

Question. Solve the following system of inequalities graphically :
x + y ≥ 1, 3x + 4y < 12, x – 2y ≤ 2, x ≥ 0, y ≥ 0
Answer: Converting the given inequations into equations,
we get
x + y = 1 …(i)
3x + 4y = 12 …(ii)
x – 2y = 2 …(iii)
x = 0, y = 0 …(iv)
Now, we draw the graphs of (i), (ii), (iii) and (iv) as shown below.

So, the shaded region represents the solution set of given system of linear inequalities.

Question. Solve graphically : 5x + y ≥ 10, 2x + 2y ≤ 12, x + 4y ≤ 12, x ≥ 3, y ≥ 0.
Answer: Converting the given inequalities into equalities, we get
5x + y = 10 …(i)
2x + 2y = 12 ⇒ x + y = 6 …(ii)
x + 4y = 12 …(iii)
x = 3 …(iv)
Now, draw the graphs of (i), (ii), (iii) and (iv) as shown below.

So, the shaded region represents the solution set of the given system of linear inequalities.

Question. Solve the following system of inequalities graphically :
x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Answer: Converting the given inequations into equations,
we get x + 2y = 10, x + y = 1, x – y = 0,
x = 0, y = 0
Now, we draw the graphs of above equations as shown below.

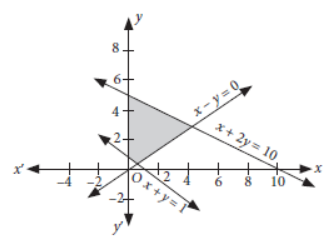
So, the shaded region represents the solution set of given system of linear inequalities.

Question. Solve graphically : 2x + 3y ≥ 3, x – y ≤ 1, 3x + 4y ≤ 12, y ≥ 2, x ≥ 0.
Answer: Converting the given inequations into equations, we get
2x + 3y = 3 …(i)
x – y = 1 …(ii)
3x + 4y = 12 …(iii)
y = 2 …(iv)
Now, draw the graphs of (i), (ii), (iii) and (iv) as shown below.

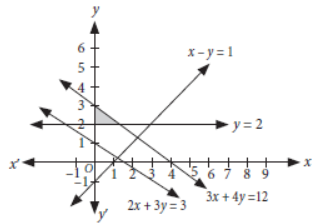
So, the shaded region represents the solution set of the given system of linear inequalities.

Case Based Questions :

Case I : Read the following passage and answer the questions from 41 to 45.
Reema went to a stationary shop with ₹100 to buy notebooks. The price of each notebook is ₹25.
Let x denotes the number of notebooks .

Question. The graph representing the above situation is

Question. If Reema gets discount of `5 on each notebook, then the maximum number of notebooks that she can buy is
(a) 2
(b) 3
(c) 4
(d) 5

Question. If Reema gets 25 extra from her mother, then the inequality representing the given situation is
(a) 25x ≥ 125
(b) 25x ≤ 125
(c) 25x ≥ 100
(d) 25x ≤ 100.

Question. The inequality which represents the above situation is
(a) 25x > 100
(b) 25x ≥ 100
(c) 25x < 100
(d) 25x ≤ 100

Question. The maximum number of notebooks that Reema can buy is
(a) 2
(b) 3
(c) 4
(d) 5.

Case II : Read the following passage and answer the questions from 46 to 50.
Amit’s mother gave him `200 to buy some packet of rice and maggi from the market. The cost of one packet of rice is ₹30 and that of one packet of maggi is ₹20. Let x denotes the number of packet of rice and y denotes the number of packet of maggi. 

Question. If he buys 4 packets of rice and spends entire amount of ₹200, then the maximum number of packets of maggi that he can buy is
(a) 3
(b) 4
(c) 5
(d) 6

Question. The maximum value of x and y respectively, if he spends his entire amount is
(a) 4, 6
(b) 4, 3
(c) 4, 5
(d) 5, 5.

Question. The inequality that represents the given situation is
(a) 30x + 20y > 200
(b) 30x + 20y ≥ 200
(c) 30x + 20y < 200
(d) 30x + 20y ≤ 200

Question. If he buys 3 packets of rice and 2 packets of maggi, then the amount that he paid is
(a) ₹110
(b) ₹120
(c) ₹130
(d) ₹140

Question. The graph representing the given situation is

Case III : Read the following passage and answer the questions from 51 to 55.
Rita and Neha wants to buy some pencils and erasers. Rita has ₹12 whereas Neha has ₹10 with her. Let x denotes the number of pencils and y denotes the number of erasers.

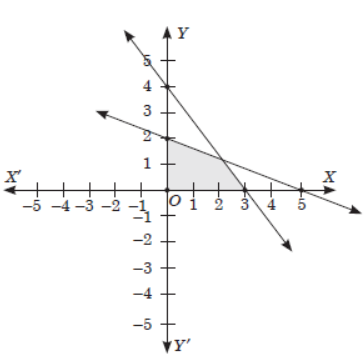
Question. The range of x in the given graph is
(a) (0, 4)
(b) [0, 4]
(c) [0, 3]
(d) (0, 3)

Question. The point lies in the given shaded region is
(a) (1, 2)
(b) (1/2, 3/2)
(c) (2, 2)
(d) (1, 3)

Question. The given region is bounded by the points
(a) (0, 0), (3, 0), (2, 0), (15/7, 8/7)
(b) (0, 0), (0, 3), (2, 0), (14/7, 8/7)
(c) (0, 0), (3, 0), (0, 2), (8/7, 14/7)
(d) (0, 0), (3, 0), (0, 2), (15/7, 8/7)

Question. The inequalities that represent the above shaded region are
(a) 4x + 3y ≤ 12, 5x + 2y ≤ 10 and x, y ≥ 0
(b) 4x + 3y ≤ 12, 2x + 5y ≤ 10 and x, y ≥ 0
(c) x + 2y ≤ 12, 2x + 5y ≤ 10 and x, y ≥ 0
(d) 3x + 4y ≤ 12, x + y ≤ 10 and x, y ≥ 0

Question. The point of intersection of inequalities that represent the given situation is
(a) (8/7 , 15/7)
(b) (14/7 , 8/7)
(c) (15/7 , 8/7)
(d) (8/7 , 14/7)