Permutations and Combinations Class 11 Mathematics Important Questions

Please refer to Permutations and Combinations Class 11 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 11 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 11 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 11.

Class 11 Mathematics Important Questions Permutations and Combinations

Assertion & Reasoning Based MCQs

(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.

Question. Assertion : Number of rectangles on a chess board is ⁸C₂ × ⁸C₂.
Reason : To form a rectangle, we have to select any two of the horizontal line and any two of the vertical line.

Question. Assertion : Number of lines formed by joining n points on a circle (n ≥ 2) is n(n-1)/2 .
Reason : C(n,2) = n(n-1)/2 .

Question. Assertion : If n is a positive integer, then n(n2 – 1) (n +2) is divisible by 24.
Reason : Product of r consecutive whole numbers is divisible by r.

Question. Assertion : The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is ⁹C₃.
Reason : The number of ways of choosing any 3 places, from 9 different places is 9C3.

Question. Assertion : Product of five consecutive natural numbers is divisible by 4!
Reason : Product of n consecutive natural numbers is divisible by (n + 1)!.

Very Short Answer Type Questions :

Question. Determine n, if C(2n, 3) : C(n, 3) = 11 : 1.
Answer: Here, C(2n, 3) : C(n, 3) = 11 : 1
⇒ ²ⁿC3 : ⁿC₃ = 11 : 1

⇒ 4 (2n–1) = 11 (n –2)
⇒ 8n – 4 = 11n – 22 ⇒ 3n = 18 ⇒ n = 6.

Question. Find n, if C(25, n + 5) = C(25, 2n – 1).
Answer: Here, C(25, n + 5) = C(25, 2n – 1)
⇒ 25Cn+5 = 25C2n–1
⇒ 25 = n + 5 + 2n – 1 or n + 5 = 2n – 1
( ∴ nCa = nCb ⇒ n = a + b or a = b)
⇒ 25 = 3n + 4 or n = 6
⇒ 3n = 21 or n = 6
Hence, n = 7 or n = 6

Question. If nC3 = nC4, find nC7.
Answer: Here, nC3 = nC4
⇒ n = 3 + 4 = 7 ( nCa = nCb ⇒ a = b or n = a + b)
∴ 7C7 = 1

Question. If 10Cx = 10Cx + 4, then find the value of x.
Answer: Given, 10Cx = 10Cx+4
⇒ 10 = x + x + 4 ⇒ 6 = 2x ⇒ x = 3.

Question. Given 4 flags of different colours, how many different signals can be generated, if a signal requires the use of 2 flags one below the other?
Answer: Here, the upper place of the flag can be filled in 4 ways by using the 4 flags of different colours.
Now, the lower place of the flag can be filled in 3 ways by using the remaining 3 flags of different colours.
∴ Total number of signals can be generated
= 4 × 3 = 12

Question. If nC5 = nC7, then find n.
Answer: Given, nC5 = nC7 ⇒ n = 5 + 7 = 12

Question. If n + 1C2 = 45. Find n.
Answer: Here, n+1C2 = 45 ⇒ (n+1)!/2!(n-1) = 45
⇒ n(n+1)(n-1)!/2(n-1)! = 45
⇒ n(n + 1) = 90 ⇒ n2 + n –90 = 0
⇒ (n + 10)(n – 9) = 0 ⇒ n = –10 or 9
⇒ n = 9 [ n = – 10 (Rejected)]

Question. If C(n, 8) = C(n, 6), then find C(n, 2).
Answer: We have, nC8 = nC6 ⇒ n = 6 + 8 = 14
∴ C(n,2) = C(14,2) = ¹⁴C₂ = 14!/2!12! = 91

Question. If nC10 = nC3, then find nC3.
Answer: We have ⁿC₁₀ = ⁿC₃ ⇒ n = 10 + 3 = 13
Hence, ¹³ C₃ = 13!/3!10! = 13 x 12 x 11 x 10! /3 x 2 x 10!
= 26 × 11 = 286

Question. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?
Answer: Here, 3-digit numbers are to be formed using digits
1 to 9 with no digit repeated.
This can be done in 9 × 8 × 7 = 504 ways.

Short Answer Type Questions :

Question. How many words (with or without meaning) of three distinct English alphabets are there?
Answer: There are 26 distinct English alphabets.
First alphabet can be chosen in 26 ways.
Second alphabet can be chosen in 25 ways.
Third alphabet can be chosen in 24 ways.
∴ Total number of three letter words
= 26 × 25 × 24 = 15600

Question. If there are 5 boys and 5 girls in a class, then in how many ways they can be seated in a row such that
(i) No two girls sit together?
(ii) All the girls never sit together?
Answer: (i) Since no two girls sit together
∴ Seating arrangement should be

⇒ There are six positions of seating for girls.
∴ Required number of ways = 5P5 × 6P5 = 5! × 6!
(ii) Required ways
= Total arrangements – Number of ways
when all the girls sit together = 10! – 5! 6!

Question. How many words, each of 3 vowels and 2 consonants can be formed from the letters of the word ‘INVOLUTE’?
Answer: Number of letters in the word = 8
Number of vowels in the word = 4 (I, O, U, E)
Number of consonants in the word = 4 (N, V, L, T)
Out of 4 vowels, we have to select 3.
Out of 4 consonants, we have to select 2.
Also, we have to arrange 3 vowels and 2 consonants.
∴ Required number of words = C(4, 3) · C(4, 2) · 5!
= 4 x 4 x 3/2 x 120 = 2880

Question. A convex polygon has 65 diagonals. Find the number of sides of the polygon.
Answer: Let number of sides or vertices be n
∴ Number of diagonals = nC2 – n 
⇒ 65 = nC2 – n ⇒ 65 = n(n-1)/2 – n
⇒ n2 – 3n = 130
⇒ (n – 13)(n + 10) = 0
⇒ n = 13 or n = – 10 (Rejected)

Question. A committee of 7 has to be formed from 9 boys and 4 girls. In how may ways can this be done when committee consist of (i) At least 3 girls (ii) At most 3 girls?
Answer: Number of boys = 9, number of girls = 4
Total members in a committee = 7
(i) Number of ways forming a committee having at
least 3 girls = ⁴C₃ × ⁹C₄ + ⁴C₄ × ⁹C₃ = 504 + 84 = 588
(ii) Number of ways forming a committee having at most
3 girls = ⁴C₃ × ⁹C₄ + ⁴C₂ × ⁹C₅ + ⁴C₁ × ⁹C₆ + ⁴C₀ × ⁹C₇
= 504 + 756 + 336 + 36 = 1632

Question. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that :
(i) Repetition of the digits is allowed?
(ii) Repetition of the digits is not allowed?
Answer: (i) There are five digits, 1, 2, 3, 4 and 5. Each digit can be selected any number of times. Hence, we can select first digit in 5 ways. The second digit and third digit can also be selected in 5 ways.
∴ The number of ways in which the selection of three
digits can be made = 5 × 5 × 5 = 125.
(ii) Under the restriction, first digit can be selected in
5 ways. After the selection of first digit four digits are
left. Second digit can be selected in 4 ways and third
digit can be selected in 3 ways.
∴ Required total no. of ways = 5 × 4 × 3 = 60

Question. A polygon has 44 diagonals. If n denotes the number of vertices of polygon. Find the value of n.
Answer: Here, number of vertices or sides = n
∴ Number of diagonals = nC2 – n
⇒ 44 = nC2 – n ⇒ 44 = n(n-1)/2 – n
⇒ n2 – 3n – 88 = 0 ⇒ (n + 8) (n – 11) = 0
⇒ n = 11 or n = – 8 (Rejected)

Question. How many numbers greater than 1000000 can be formed by using the digits 1, 2, 3, 4, 0, 5, 3?
Answer: Digits are 1, 2, 0, 3, 4, 5, 3
Number greater than 10,00,000 by using the given digits
are = 7!/2! 
But numbers starting with ‘0’ are not greater than 10,00,000.
Total numbers starting with ‘0’ are = 6!/2!
From (i) and (ii), numbers greater than 10,00,000 are = 7!/2! – 6!/2! = 2160 

Question. A committee of 3 persons is to be constituted from a group of 2 men and 3 women. In how many ways can this be done? How many of these committees would consist of one man and two women?
Answer: There are 2 men and 3 women in the group.
A committee of 3 persons can be selected in
5C3 = 10 ways
A committee consisting of 1 man and 2 women
= 2C1 × 3C2 = 2 × 3 = 6 ways.

Question. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
Answer: Let the consecutive even positive integers be 2n, 2n + 2
According to question, 2n > 5 ⇒ n > 5/2
and 2n + 2n + 2 < 23 ⇒ 4n < 21 ⇒ n < 21/4
∴ Possible values of n are 3, 4, 5.
Hence, possible pairs of consecutive even positive
integers (6, 8), (8, 10), (10, 12).

Question. If the letters of the word ‘EXAMINATION’ are arranged in all possible ways as listed in dictionary. How many words are there in the list in which the first word start with ‘A’?
Answer: Total number of letters in the word ‘EXAMINATION’
are 11 with 2 A’s, 2I ’s and 2N ’s.
Now when word starts with A i.e., A is fixed at the
beginning of the word. Then we have to arrange the
remaining 10 letters with 2I’s, 2N’s.
Then words starting with A = 10!/2!2! = 907200
∴ Required number of words = 907200

Question. A boy has 3 library tickets and 8 books of his interest in the library. Of these 8 books, he does not want to borrow mathematics part II unless mathematics part I is also borrowed. In how many ways can he choose the three books to be borrowed?
Answer: Case (i) When mathematics part I is borrowed, then part II is also borrowed. Hence, the number of ways of selecting 1 book from 6 books is 6C1 = 6
Case (ii) When mathematics part I is not borrowed, then part II is not borrowed. So, he has to select three books out of remaining 6 books.
∴ Total number of ways of selection = 6C3 = 20
Hence, total number of ways of selection = 6 + 20 = 26

Question. How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6, if the digits can be repeated?
Answer: Let 2 be fixed at unit’s place. The ten’s place can be filled up in 6 ways. The hundred’s place can also be filled in 6 ways.
∴ Number of ways = 6 × 6 = 36
When 4 is at unit’s place, then no. of numbers that can be formed = 36.
Again when 6 is at the unit’s place, then numbers that can be formed = 36
∴ The total ways in which three digit even numbers can be formed = 36 × 3 = 108.

Question. (i) How many different numbers of 6-digit number can be formed with the digits 1, 2, 7, 0, 9, 5?
(ii) How many of them are divisible by 10?
(iii) How many of them will have zero in the ten’s place?
Answer: (i) Number of digits = 6
∴ Required number of 6-digit numbers
= P(6,6) – P(5, 5) = 6! – 5! = 720 – 120 = 600.
(ii) The numbers are divisible by 10 if 0 is in the unit place.
∴ The required numbers which are divisible by
10 = P(5, 5) = 5! = 120
(iii) The numbers having 0 in the ten’s place.
× × × × 0 ×
∴ The required numbers = P(5, 5) = 5! = 120

Question. For a set of five true or-false questions, no student has written all the correct answers, and no two students have given the same sequence of answers. What is the maximum number of students in the class, for this to be possible?
Answer: Each of the five question can be answered in 2 ways.
Hence, total number of possible different answers
= 2 × 2 × 2 × 2 × 2 = 32
There is only one sequence of all correct answers. Thus, the total number of sequences are 32 – 1 = 31. [Since no student has written all correct answers]
Now, as no two students have given the same sequence of answers, hence the maximum number of students in the class=31.

Question. How many automobile license plates can be made, if each plate contains two different letters (English alphabets) followed by three different digits?
Answer: Total number of English alphabets = 26
Number of letter to be chosen = 2
∴ Number of ways of selecting two letters = 26P2
= 26 × 25 = 650
So, number of digits = 10
∴ Number of ways of selecting 3 digits = 10P3
= 10 × 9 × 8 = 720
Hence, required license plates can be made
= 650 × 720 = 468000

Question. Everybody in a room shakes hands with everybody else. The total number of hand shakes is 66. Find the total number of persons in the room.
Answer: Let the total number of persons in the room be n.
∴ Required number of hand shakes = nC2
= n!/2!(n-2)! = n(n-1)/2
Given that, n(n-1)/2 = 66 ⇒ n(n – 1) = 132 
⇒ n2 – n – 132 = 0 ⇒ (n – 12)(n + 11) = 0
⇒ n = 12 (… n can’t be negative)

Question. The letters of the word ‘WOMAN’ are written in all possible orders and these words are written out as in a dictionary, then find the rank of the word ‘WOMAN’.
Answer: Total number of ways of arranging the given word
‘WOMAN’ as in a dictionary

∴ Required rank = 4 × 4! + 3 × 3! + 2! + 1 = 117th

Question. How many numbers greater than 1000000 can be formed by using digits 1, 2, 0, 2, 4, 2, 4?
Answer: Since, we have to form the numbers greater than
1000000 by using 1, 2, 0, 2, 4, 2, 4
So, numbers which begin with digit ‘1’ = 6!/3!2! = 60
Numbers that begin with digit ‘2’ = 6!/2!2! = 180
Numbers that begin with digit ‘4’ = 6!/3! = 120
∴ Required numbers = 60 + 180 + 120 = 360

Question. If nPr = nPr + 1 and nCr = nCr –1, then find the values of n and r.
Answer: Here, nPr = nP_{r + 1}

From (i) and (ii), we get, n = 3 and r = 2

Question. A candidate is required to answer 7 questions out of 12 questions, which are divided into two sections A and B, each containing 6 questions.
He is not permitted to attempt more than 5 questions from each section. Find the number of different ways of selecting the questions.
Answer: Since, candidate cannot attempt more than 5 questions from either section.
The number of questions attempted from each section is given in following table :

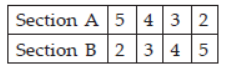
Hence, total number of possible ways
= 6C5 × 6C2 + 6C4 × 6C3 + 6C3 × 6C4 + 6C2 × 6C5
= 2[6C5 × 6C2 + 6C4 × 6C3]
= 2 [90 + 300] = 2 × 390 = 780

Question. The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and two different consonants can be formed from alphabets?
Answer: We have 5 vowels and 21 consonants our english
alphabets.
∴ Number of words formed with 2 different vowels
and 2 different consonants = ⁵C₂ × ²¹C₂
= 10 × 210 = 2100
Now, 4 selected letters can arrange themselves in 4! ways
∴ Total words formed = 2100 × 4! = 50400

Question. Eighteen guests are to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on other side of the table. Find the number of possible seating arrangements.
Answer: Since, guests are to be seated half on each side i.e.,
9 to be seated on side A and rest on side B.
Now, out of 18 guests, 4 particular guests sit on one
particular side and 3 on other side.
Now, we have 18 – 4 – 3 = 11 guests can be select 5
more for side A and 6 on side B.
Hence, selection can be done in ¹¹C₅
and, a guests on each side of table can be seated in 9! × 9!
Thus, total arrangements = ¹¹C₅ × 9! × 9!

Question. There are 15 points in a plane, out of which only 6 are in a straight line.
(i) How many different straight lines can be made?
(ii) How many triangles can be made?
Answer: (i) Number of straight lines formed joining the 15 points, taking 2 at a time = 15C2 = 105
Number of straight lines formed by joining the 6 points,
taking 2 at a time = 6C2 = 15
But, 6 collinear points when joined pairwise give only line
∴ Required number of straight lines
= 105 – 15 + 1 = 91
(ii) Number of triangles formed by joining the points, taking 3 at a time = 15C3 = 455
Number of triangles formed by joining the 6 points, taken 3 at a time = 6C3 = 20
But, 6 collinear points cannot form a triangle when taken 3 at a time.
So, required number of triangles = 455 – 20 = 435.

Question. How many words, with or without meaning can be made from the letters of the word ‘MONDAY’, assuming that no letter is repeated, if :
(i) 4 letters are used at a time,
(ii) All letters are used at a time?
Answer: MONDAY has 6 different letters, in which there are two vowels namely, A and O.
(i) If 4 letters are taken at a time, then,
Number of words = 6P4 = 6 × 5 × 4 × 3 = 360
(ii) If all the letters of word MONDAY are taken at a time, then number of words = 6! = 720.

Long Answer Type Questions :

Question. (i) How many different words can be formed with the letters of the word HARYANA?
(ii) How many of these begin with H and end with N?
(iii) In how many of these H and N are together?
Answer: (i) There are 7 letters in the word ‘HARYANA’ of which 3 are A’s and remaining all are each of its own kind.
So, total number of words = 7!/3! = 840
(ii) After fixing H in first place and N in last place, we have 5 letters out of which three A’s are alike.
So, total number of words = 5!/3! = 20.
(iii) Considering H and N together we have
7–2 + 1 = 6 letters out of which three A’s are alike. These six letters can be arranged in 6!/3! ways. But H and N can be arranged among themselves in 2! ways.
∴ Required number of words = 6!/3! x 2! = 240.

Question. From a class of 12 boys and 10 girls, 10 students are to be chosen for a competition, including atleast 4 boys and 4 girls. The two girls who won the prizes last year should be included. In how many ways can the selection be made?
Answer: There are 12 boys and 10 girls in the class. We have to select 10 students for a competition including atleast 4 boys and 4 girls. Two girls who were last year’s winner are to be included. Since two girls are already selected, now we are left with 8 girls out of which atleast 2 girls are to be selected.
We can make selection in the following ways:

First choice can be made 12C4 × 8C4

Question. A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has
(i) No girl?
(ii) Atleast one boy and one girl?
(iii) Atleast 3 girls?
Answer: (i) A team consisting no girl can be selected 7C5 ways i.e., 7 x 6/2 x 1 = 21 ways
(ii) Number of ways of selecting at least one boy and
one girl
= ⁷C₁ × ⁴C₄ + ⁷C₂ × ⁴C₃ + ⁷C₃ × ⁴C₂ + ⁷C₄ × ⁴C₁
= 7 + 84 + 210 + 140 = 441
(iii) A team having alteast 3 girls will consist of:
3 girls, 2 boys; 4 girls, 1 boy.
∴ Required no. of ways = ⁴C₃ × ⁷C₂ + ⁴C₄ × ⁷C₁
= 4 × 21 + 1 × 7 = 91 ways.

Question. If nCr : nCr + 1 = 1 : 2 and nCr + 1 : nCr + 2 = 2 : 3, then find the values of n and r.
Answer: nCr : nCr + 1 = 1 : 2 and nCr + 1 : nCr + 2 = 2 : 3

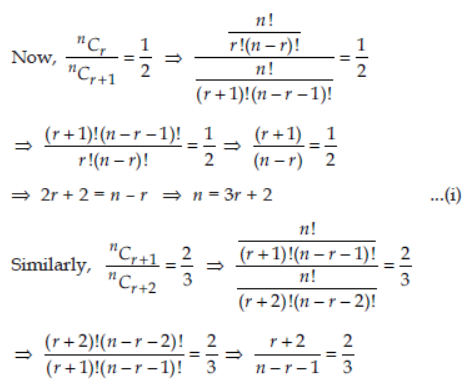
⇒ 3r + 6 = 2n – 2r – 2 ⇒ 2n = 5r + 8 …(ii)
Solving (i) and (ii), we get r = 4 and n = 14

Question. How many words with or without meaning can be formed using the letters of the word ‘DAUGHTER’, if
(i) All vowels are never together
(ii) Vowels occupy odd places?
Answer: The given word ‘DAUGHTER’ contains 8 different
letters with vowels A, U and E.
∴ Total number of words formed by using all the 8
letters of the given word = 8! = 40320
(i) The total number of words in which vowels
do not occur together = (Total number of words)
–(number of words in which vowels are always together)
= 40320 – 6! × 3P3
= 40320 – 4320 = 36000
(ii) For vowels to occupy odd places, first arrange 3
vowels in 4 odd places. This can be done in 4P3 ways
and remaining 5 alphabets can be filled in 5! ways.

∴ Required number of ways = 5! × 4P3 = 2880

Case Based Questions :

Case I : Read the following passage and answer the questions from 41 to 45 .
Sumit works at a book shop. While arranging some books on the book shelf, he observed that there are 5 History books, 3 Mathematics books and 4 Science books which are to be arranged on the shelf.

Question. Find the number of ways, if the books of same subject are put together.
(a) 4!· 2!· 3!
(b) 2!· 3!· 2!· 5!
(c) 5!· 2!· 4!
(d) 3!· 5!· 3!· 4!

Question. If we are given the number of arrangement of books as 5P2 × 3P1 × 4P1, then the arrangement is in the manner
(a) 2 History books, 2 Maths books, 3 Science books respectively.
(b) 2 History books, 3 Maths books, 2 Science books respectively.
(c) 3 History books, 2 Maths books, 2 Science books respectively.
(d) None of these

Question. In how many ways can he select either a History book or a maths book?
(a) 10
(b) 8
(c) 20
(d) 60

Question. If he select 2 History books, 1 Maths book and 1 Science book to arrange them, then find the number of ways in which selection can be made.
(a) 200
(b) 220
(c) 240
(d) 260

Question. Find the number of arrangements, if he select 3 History books, 2 Maths Books, 2 Science books are
(a) 4300
(b) 4320
(c) 4330
(d) 4380

Case II : Read the following passage and answer the questions from 46 to 50.
Reema and Seema are two friends. Reema decided to invite her friend for dinner. When she tried to call her for invitation first she forgot her mobile number. She had only first 4-digits i.e., 9, 7, 6 and 5.

Question. If digits 3 and 4 come together, then number of ways to find mobile number (when repetition is not allowed), is
(a) 200
(b) 220
(c) 240
(d) 260

Question. The number of ways to find 10 digit mobile number that digits 3 and 4 not occur together (when repetition is not allowed) is
(a) 720
(b) 240
(c) 400
(d) 480

Question. Find the number of ways to find mobile number so that 4 become the unit digit and repetition is not allowed.
(a) 100
(b) 110
(c) 120
(d) 130

Question. If the repetition of the digits is not allowed, then find the number of ways to find her mobile number.
(a) 5!
(b) 6!
(c) 7!
(d) 8!

Question. If the repetition is allowed, then the number of ways to find 10 digit mobile number is
(a) 56
(b) 76
(c) 96
(d) 106

Case III : Read the following passage and answer the questions from 51 to 55.
Riya and her 5 friends went for a trip to Shimla.
They stayed in a hotel. There were 4 vacant rooms A, B, C and D. Out of these 4 vacant rooms, two room A and B were double share rooms and two rooms C and D can contain one person each.

Question. The total number of ways of accommodating Riya and her friends in these 4 vacant rooms is
(a) 150
(b) 160
(c) 170
(d) 180

Question. If room A is filled with 2 persons, then find the number in which rooms C and D can be filled.
(a) 4
(b) 12
(c) 8
(d) 10

Question.

Question. The number of ways in which room A can be filled is
(a) 10
(b) 15
(c) 20
(d) 25

Question. If room A and B are already filled each, then find the number of ways in which room C can be filled.
(a) 2
(b) 4
(c) 6
(d) 8