Conic Sections Class 11 Mathematics Important Questions

Please refer to Conic Sections Class 11 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 11 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 11 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 11.

Class 11 Mathematics Important Questions Conic Sections

Assertion & Reasoning Based MCQs

(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.

Question. If the distances of foci and vertex of hyperbola from the centre are c and a respectively, then 
Assertion : Eccentricity is always less than 1.
Reason : Foci are at a distance of ae from the centre.

Question. Assertion : The sum of focal distances of a point on the ellipse 9x² + 4y² – 18x – 24y + 9 = 0 is 4. 
Reason : The equation 9x² + 4 y² – 18x – 24y + 9 = 0 can be expressed as 9(x – 1)² + 4(y – 3)² = 36.

Question. Assertion : A line through the focus and perpendicular to the directrix is called the x-axis of the parabola. 
Reason : The point of intersection of parabola with the axis is called the vertex of the parabola.

Question. Parabola is symmetric with respect to the axis of the parabola. 
Assertion : If the equation of standard parabola has a term y², then the axis of symmetry is along the x-axis.
Reason : If the equation of standard parabola has a term x², then the axis of symmetry is along the x-axis.

Question. Assertion : The length of major and minor axes of the ellipse 5x² + 9y² – 54y + 36 = 0 are 6 and 10, respectively. 
Reason : The equation 5x² + 9y² – 54y + 36 = 0 can be expressed as 5x² + 9(y – 3)² = 45.

Very Short Answer Type Questions :

Question. Find the equation of a parabola with vertex at origin and axis along x-axis and passing through the point (2, 8).
Answer: Let the equation of the parabola with vertex at
origin and axis along x-axis is y2 = 4ax …(i)
(i) passes through (2, 8).
∴ (8)2 = 4a(2) ⇒ a = 8
Putting value of a in (i), we get required equation of
parabola y2 = 32x.

Question. What is the eccentricity of the hyperbola 9y2 – 4×2 = 36 ?
Answer: Given 9y2 – 4×2 = 36 ⇒ y2/4 – x2/9 = 1
a2 = 4, b2 = 9
∴ Eccentricity, e =√a2+b2/a = √4+9/2 = √13/2 . 

Question. If the distance of the focus of a parabola from its directrix is 4, find the length of the latus rectum.
Answer: Since, distance of the focus of a parabola from its
directrix is 2a.
∴ Given, 2a = 4 ⇒ a = 2
Now, length of latus rectum = 4a = 8.

Question. Find the eccentricity of the ellipse :
x2/25 + y2/9 = 1 .
Answer: Given, equation of ellipse is x2/25 + y2/9 = 1
Major axis is along x-axis as 25 > 9.
Here, a2 = 25, b2 = 9.
∴  Eccentricity (e) =√1-b2/a2 = √1-9/25 = 4/5

Question. What is the eccentricity of hyperbola whose vertices and foci are (±2, 0) and (±3, 0) respectively?
Answer: Vertices are (±2, 0), foci are (±3, 0)
⇒ a = 2, c = 3 ∴ e = c/a = 3/2 . 

Question. Find the equation of the ellipse with foci at (± 5, 0) and x = 36/5 as one of the directices. 
Answer: We have ae = 5, a/e = 36/5 which gives a2 = 36
or a = 6. Therefore, e = 5/6 .
Now b = a√1-e2 = 6 √1-25/36 = √11 . Thus, the equation
of the ellipse is x2/36 + y2/11 = 1 .

Question. Find the coordinate of the focus of the parabola y2 = 12x.
Answer: Given, parabola y2 = 12x = 4ax
⇒ 4a = 12 or a = 3 ∴ Focus = (3, 0)

Question. Find the centre of the circle x² + y² + 2y = 0.
Answer: Equation of circle is x² + y² + 2y = 0 …(i)
General equation of circle is x² + y² + 2gx + 2fy + c = 0,
with centre (–g, –f )
On comparing general equation with (i), we get 2g = 0,
2f = 2 ∴ g = 0, f = 1
So, the centre of given circle is centre (0, –1)

Question. What is the eccentricity of the curve 4×2 + y2 = 100 ?
Answer: Given, 4×2 + y2 = 100 ⇒ x2/25 |+ y2/100 = 1
Here, a2 = 100, b2 = 25
∴ c =√a2-b2 = √100-25 = √75 = 5√3
∴  e = c/a = 5√3/10 = √3/2 . 

Question. Find the equation of the circle which passes through the point (4, 5) and has its centre at (2, 2).
Answer: As the circle is passing through the point (4, 5) and its centre is (2, 2) so its radius is √(4−2)2 +(5−2)² = 13.
Therefore the required equation of circle is (x – 2)2 + (y – 2)2 = 13.

Short Answer Type Questions :

Question. Find the co-ordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum of the parabola x² = – 9y.
Answer: Given parabola is x2 = – 9y which is of the form
x2 = –4ay
where 4a = 9 ⇒ a = 9/4 .
Hence, it is symmetric about
y-axis.
Coordinates of focus are     

(0, – a) = (0,-9/4)
Axis of the parabola is x = 0.
Equation of directrix is y = a i.e., y = 9/4 
Length of latus rectum = 4a = 4 x (9/4) = 9 units.

Question. Find the eccentricity of the ellipse 25x² + 9y² – 150x – 90y + 225 = 0.
Answer: We have 25×2 + 9y2 – 150x – 90y + 225 = 0
⇒ 25 (x2 – 6x) + 9(y2 – 10y) = – 225
⇒ 25 (x2 – 6x + 9) + 9(y2 – 10y + 25) = 225
⇒ 25 (x – 3)2 + 9 (y – 5)2 = 225
⇒ (x2-3)2/9 + (y-5)2/25 = 1
The eccentricity is given by
e = √1-a2/b2 = √1-9/25 = 4/5

Question. The foci of an ellipse are (±2, 0) and its eccentricity is 1/3 . Find the equation of ellipse.
Answer: Let equation of ellipse be x2/a2 + y2/b2 = 1 .
The coordinates of foci are (± ae, 0).
∴ ae = 2 ⇒ a × 1/3 = 2 ⇒ a = 6
Now, b2 = a2 (1 – e 2) ⇒ b2 = 36(1-1/9) = 32
Thus, equation of required ellipse is x2/36 + y2/32 = 1.

Question. Write the equation of ellipse whose vertices are (±5, 0) and foci (±4, 0).
Answer: Vertices are (±5, 0); foci (±4, 0)
Ellipse is x2/a2 + y2/b2 = 1
We have, a = 5, c = 4 = √a²-b²
⇒ 16 = 25 – b2 ⇒ b2 = 9
Substituting for a, b in (i), we get
x2/25 + y2/9 = 1 as equation of the ellipse.

Question. If the eccentricity of an ellipse is 5/8 and the distance between its foci is 10, then find the latus rectum of the ellipse.
Answer: Let the equation of the required ellipse be x2/a2 + y2/b2 = 1
and let e be its eccentricity.
We have, e = 5/8 and 2ae = 10 ⇒ ae = 5
⇒ a = 8
∴ b2 = a2 (1-e2) ⇒ b2 = 64(1-25/64) = 39
Hence, length of the latus rectum
= 2b2/a = 2 x 39/8 = 39/4

Question. If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
Answer: The given lines 3x – 4y + 4 = 0 &
2(3x – 4y –7/2) = 0 are parallel to each other. And distance between given parallel lines gives the diameter of the circle. 

Question. If the abscissae and the ordinates of two points A and B be the roots of ax2 + bx + c = 0 and a′ y2 + b′ y + c′ = 0 respectively, show that the equation of the circle described on AB as diameter is aa′ (x2 +y2) + a′bx + ab′ y + (ca′ + c′a) = 0.
Answer: Let (x1, y1) and (x2, y2) be the coordinates of points
A and B respectively.
It is given that x1, x2 are roots of ax2 + bx + c = 0 and
y1, y2 are roots of a′ y2 + b′ y + c′ = 0.
∴ x + x = − b/a , x1 x2 = c/a ,
y1+y2 = b’/a’ and y1y2 = c’/a’
The equation of the circle with AB as diameter is
(x – x₁) (x – x₂) + (y –y₁) (y – y₂) = 0
⇒ x2 + y2 – x (x1 + x2) – y(y1 + y2) + x1x2 + y1y2 = 0.
⇒ x² + y² – x(-b/a) – (-b’/a’) y+ c/a + c’/a’ = 0
⇒ aa′(x2 + y2) + a′ bx + ab′ y + (ca′ + c′ a) = 0

Question. Find the equation of the circle whose centre lies on the line x – 4 y = 1 and which passes through the points (3, 7) and (5, 5).
Answer: Let equation of required circle be
x2 + y2 + 2gx + 2fy + c = 0 …(i)
∴ (3, 7) and (5, 5) lie on (i).
∴ (3)2 + (7)2 + 2(3)g + 2(7)f + c = 0
⇒ 6g + 14f + c = – 58 …(ii)
and (5)2 + (5)2 + 2(5)g + 2(5) f + c = 0
⇒ 10g + 10f + c = –50 …(iii)
(iii) – (ii) gives 4g – 4f = 8 ⇒ g – f = 2 …(iv)
Also, centre (– g, – f) lies on x – 4y = 1
∴ – g – 4(–f) = 1
or –g + 4f = 1 …(v)
Solving (iv) and (v), f = 1, g = 3
Putting these values in (iii), we get
30 + 10 + c = – 50 ⇒ c = – 90
∴ Required equation of circle is
x2 + y2 + 6x + 2y – 90 = 0.

Question. Find the equation of the circle which passes through the points (2, –2) and (3, 4) and whose centre lies on x + y = 1
Answer: Let circle be (x – h)2 + (y – k)2 = r2 …(i)
Circle (i) passes through the points (2, –2) and (3, 4).
∴ (2 – h)2 + (–2 – k)2 = r2 …(ii)
and (3 – h)2 + (4 – k)2 = r2 …(iii)
Also centre (h, k) lies on x + y = 1
∴ h + k = 1 …(iv)
From (ii) and (iii), we get
(2 – h)2 + (–2 – k)2 = (3 – h)2 + (4 – k)2
⇒ 4 – 4h +h2 + 4 + 4k + k2 = 9 – 6h + h2 + 16 – 8k + k2
⇒ 2h + 12k = 17 …(v)
Solving (iv) and (v), we get, h = −1/2 , k = 3/2
Substituting for h, k in (iii), we get
(3+1/2)2 + (4-3/2)2 = r2
⇒ 49/4 + 25/4 = r2 ⇒ 74/4 = r2 ⇒ r = √74/2
Substituting for h, k, r in (i), we get
(x+1/2)2 + 9y-3/2)2 = 74/4
⇒ x2 + x +1/4 + y2 – 3y + 9/4 = 74/4
⇒ x2 + y2 + x –3y – 16 = 0 is the required equation.

Question. Find the equation of a circle whose centre is (1, –2) and which passes through the centre of the circle x2 + y2 – 4x – 6y + 11 = 0.
Answer: Let equation of circle with centre (1, – 2) and radius
r be (x – 1)2 + (y + 2 )2 = r 2 …(i)
and centre of given circle x2 + y2 – 4x – 6y + 11 = 0 is (2, 3).
Q (i) passes through (2, 3).
∴ (2 – 1)2 + (3 + 2)2 = r2
⇒ 1 + 25 = r2 ⇒ r2 = 26.
Put r2 = 26 in (i), we get
(x – 1)2 + (y + 2)2 = 26
⇒ x2 + 1 – 2x + y2 + 4 + 4y = 26
⇒ x2 + y2 – 2x + 4y – 21 = 0

Question. Find the equation of the parabola whose focus is at (–1, –2) and the directrix is the line x – 2y + 3 = 0.
Answer: Let P(x, y) be any point on the parabola whose focus is S(–1, –2) and the directrix x – 2y + 3 = 0.
Draw PM perpendicular from P(x, y) on the directrix
x – 2y + 3 = 0.
Then, by definition
SP = PM ⇒ SP² = PM²           

⇒ (x+1)² + (y+2)² = (x-2y+3)²/√1+4
⇒ 5[(x + 1)² + (y + 2)²]
= (x – 2y + 3)²
⇒ 5(x² + y² + 2x + 4y + 5)
= (x² + 4y² + 9 – 4xy + 6x – 12y)
⇒ 4x² + y² + 4xy + 4x + 3²y + 16 = 0 is the equation of the required parabola.

Question. Find the equation of the hyperbola satisfying the given conditions: vertices (0, ± 5), foci (0, ± 8).
Answer: Let the equation of the hyperbola be
-x²/a² + y²/b² = 1
Its vertices are at (0, ± 5) and foci are at (0, ± 8).
∴ b = 5 and be = 8.
Now, a2 = b²(e² –1) ⇒ a² = (be)² – b² = 64 – 25 = 39
Substituting the values of a and b in (i), we get
– x²/39 + y²/25 = 1 as the equation of the hyperbola.

Question. Find the equation of ellipse with centre at origin, major axis along the x-axis and passing through the points (4, 3) and (1, 4).
Answer: Let equation of ellipse be 
x2/a2 + y2/b2 = 1 , a > b
Since, (4, 3) and (1, 4) lies on it.
∴ 16/a2 + 9/b2 = 1 …(ii) and 1/a2 + 16/b2 = 1
From (ii) and (iii) we get, 16/a2 + 9/b² = 1/a² + 16/b²
⇒ 15/a² = 7/b² ⇒ a² = 15/7 b²
Using (iv) in (ii), we get
16/15b² x 7 + 9/b² = 1 ⇒ 247/15b² = 1 ⇒ b² = 247/15
Using (v) in (iv), we get a² = 247/7
Putting required values in (i), we get
x²/(247/7) + y²/(247/15) = 1 ⇒ 7x² + 15y² = 247

Question. An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide  at the base. How wide is it 2 m from the vertex of the parabola?
Answer:  

Let point P(x1, –2) lies on parabola.
∴ (x1)² = -5/8 x (-2) ⇒ x12 = 5/4 ⇒ x1 = ± √5/2
∴ Width of parabola 2 m from vertex is
2 x √5/2 = √5 m = 2.23 m

Question. Find the equation of the hyperbola whose foci are (±3 √5,0) and the length of latus rectum is 8 units.
Answer: Let hyperbola be x²/a² – y²/b² = 1
Foci are (± 3 5,0) and latus rectum is 8.
∴ c =3√5 and ab2/a = 8 ⇒ b² = 4a
∴ √a² + b² = 3 √5
⇒ a² + b² = 45 ⇒ a² + 4a – 45 = 0
⇒ (a + 9) (a –5) = 0
∴ a = 5 Q a = – 9, (not possible)
So, b² = 4 × 5 = 20
Substituting for a, b in (i), we get hyperbola as
x²/25 – y²/20 – 1 .

Question. Find the equation of ellipse with centre at origin, major axis along x-axis, foci (± 2, 0) and passing through the point (2, 3).
Answer: Let equation of ellipse with centre at origin and
major axis along x-axis be x²/a² + y²/b² = 1

Now, S′P + SP = 2a
⇒ √{2 − (−2)}² + (3 − 0)² + (2 − 2)² + (3 − 0)² = 2a
⇒ √16 + 9 + √9 = 2a ⇒ 2a = 5 + 3 = 8
⇒ a = 4
Also, foci = (+ 2, 0) = (± a² − b² , 0)
⇒ a² – b² = 4 ⇒ 16 – b² = 4 ⇒ b² = 12
Putting values of a2 and b2 in (i), we get
x²/16 + y²/12 =1 , which is the required equation of ellipse.

Question. Find the equation of ellipse whose foci are (0, ±6) and length of minor axis is 16 units. Also find the coordinates of the points where the ellipse cuts y-axis and its latus rectum.
Answer: Since foci of ellipse is (0, ± 6)
∴ Major axis lies along y-axis.
Let equation of ellipse be x²/a² + y²/b² = 1 , b > a
Also, length of minor axis = 2a = 16 ⇒ a = 8
∴ b² – a² = 36 ⇒ b² – 64 = 36 ⇒ b = 10
Putting the values of a and b in (i), we get
x²/64 + y2/100 = 1 ,  which is the required equation of ellipse.
Points where ellipse cuts y-axis = vertex = (0, + b) = (0, + 10).
Latus rectum = 2a²/b = 2(64)/10 = 128 units

Question. Find the eccentricity of the hyperbola x²/a² – y²/b² = 1 which passes through the points (3,0) and (3 √2 , 2).
Answer: Given that the hyperbola x2/a2 -y2/b2 = 1 is passing through the points (3, 0) and (3 √2 ,2), so we get a² = 9 and b² = 4.
Again, we know that b2 = a2 (e2 – 1). This gives
4 = 9 (e2 – 1) ⇒ e² = 39/9 ⇒ e = √13/3

Question. Find the equation of the hyperbola, the length of whose latus rectum is 8 and eccentricity is 3/√5 .
Answer: Let equation of hyperbola be x2/a2 – y2/b2 = 1 Given,
2b2/a = 8 ⇒ b = a
But, b2 = a2(e2 –1)
∴ a2(e2 –1) = 4a ⇒ a (e2 – 1) = 4
⇒ a(9/5-1) = 4 ⇒ a = 5 ∴ b2 = 4 × 5 = 20
Thus, equation of required hyperbola is
x²/25 – y²/20 = 1 .

Question. Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre lies on the line 4 x + y = 16.
Answer: Let equation of the circle be
x2 + y2 + 2gx + 2fy + c = 0 …(i)
∴ (4, 1) and (6, 5) lie on (i).
∴ (4)2 + (1)2 + 2(4)g + 2(1)f + c = 0
⇒ 8g + 2f + c = –17 …(ii)
and (6)2 + (5)2 + 2(6)g + 2(5) f + c = 0
⇒ 12g + 10f + c = – 61 …(iii)
(iii) – (ii) gives 4g + 8f = –44 …(iv)
Also, centre (–g, –f ) lies on 4x + y = 16.
∴ – 4g – f = 16 …(v)
Solving (iv) and (v), g = – 3, f = – 4
Putting values of g and f in (ii) we get
8(–3) + 2 (–4) + c = –17 ⇒ c = 15
∴ Required equation of circle is
x2 + y2 – 6x – 8y + 15 = 0

Question. Find the equation of the ellipse with focus at (1, 1) and eccentricity 1/2 and directrix x – y + 3 = 0. Also, find the equation of its major axis .
Answer: Let P ( x, y) be a point on the
ellipse. Then, by definition SP = ePM     

∴ SP = 1/2 PM     

⇒ 8[(x – 1)² + (y – 1)2] = (x – y + 3)²
⇒ 7x² + 7y² + 2xy – 22x – 10y + 7 = 0 is the required
equation of the ellipse.
The major axis is a line perpendicular to the directrix
and passing through the focus.
Therefore, the equation of the major axis is
y – 1 = – 1 (x – 1) ⇒ x + y – 2 = 0.

Question. The foci of a hyperbola coincide with the foci of the ellipse x2/25 + y2/9 = 1 . Find the equation of the hyperbola if its eccentricity is 2.
Answer: The equation of the ellipse is x2/25 + y2/9 = 1 .
∴ a2 = 25 and b2 = 9
Eccentricity of ellipse = √1-b2/a2 = √1-9/25 = 4/5
So, the coordinates of foci are (±4, 0)
Since the coordinates of foci of hyperbola coincide
with the foci of the ellipse. So the coordinates of foci of hyperbola are (± 4, 0).
Let equation of required hyperbola is x2/a2 – y2/b’2 = 1
Let e’ be the eccentricity of required hyperbola.
then a’e’ = 4 ⇒ 2a’ = 4 ⇒ a’ = 2
∴ b’ 2 = a’ 2 (e’ 2 – 1) ⇒ b’ 2 = 4 (4 – 1) = 12
Thus, equation of required hyperbola is
x²/4 – y²/12 = 1 .

Question. Find the equation of the hyperbola whose conjugate axis is 5 and the distance between the foci is 13.
Answer: Let 2 a and 2 b be the transverse and conjugate axes and e be the eccentricity. Let the centre be the origin and the transverse and the conjugate axes the coordinate axes.
Then, the equation of the hyperbola is
x²/a² – y²/b² = 1
We have, 2b = 5 and 2ae = 13.
Now, b² = a² (e² – 1) ⇒ b² = a² e² – a²
⇒ 25/4 = 169/4 – a² ⇒ a² = 144/4 ⇒ a = 6 .
Substituting the values of a and b in (i), the equation of the hyperbola is
x²/36 – y²/25/4 = 1 ⇒ 25x² – 144y² = 900.

Question. An equilateral triangle is inscribed in the parabola y2 = 4 ax, where oLet equation of ellipse with centre at origin andne vertex is at the vertex of the parabola. Find the length of the side of the triangle.
Answer: Let DAPQ be an equilateral triangle with side of length l.
Since each angle of an equilateral triangle is 60°. Then
∠PAR = 30°
cos30° = AR/l         

⇒ AR = l√3/2 
and PR = l/2
Thus, (l√3/2 , l/2) are the coordinates of point P.
Since point P also lies on the parabola y² = 4ax
∴ (l/2)² = 4a x (l√3/2) ⇒ l = 8a√3
Hence, length of the side of the triangle is 8a√3 .

Question. Find the equation of the ellipse whose focus is (1, 0), the directrix is x + y + 1 = 0 and eccentricity is equal to 1/ 2 .
Answer: Let S(1, 0) be the focus and ZZ’ be the directrix. Let P(x, y) be any point on the ellipse and PM be perpendicular from P on the directrix. Then, by definition
SP = e.PM, where e = 1/√2           

⇒ 4[x – 1)² + y2] = (x + y + 1)2
⇒ 4x² + 4y² – 8x + 4 = x² + y² + 1 + 2xy + 2x + 2y
⇒ 3x² + 3y² – 2xy – 10x – 2y + 3 = 0
This is the equation of the required ellipse.

Long Answer Type Questions :

Question. Find the equation of the parabola whose focus is (1, 1) and tangent at the vertex is x + y = 1.
Answer: Let S be the focus and A be the vertex of the parabola. Let K be the point of intersection of the axis and directrix. Since axis is a line passing through S (1, 1) and perpendicular to x + y = 1. So, let the equation of the axis be x – y + l = 0.     

This will pass through S(1, 1), if
1 – 1 + l = 0 ⇒ l = 0
So the equation of the axis is
x – y = 0
The vertex A is the point of intersection of x – y = 0 and x + y = 1. Solving these two equations, we get x = 1/2 and y = 1/2.
Let (x1, y1) be the coordinates of K. As A is the midpoint of SK.
∴ x1 + 1/2 = 1/2 , y1+1/2 = 1/2 ⇒ x1 = 0 , y1 = 0
So, the coordinates of K are (0,0). Since directrix is a line
passing through K (0,0) and parallel to x + y = 1. Therefore,
equation of the directrix is
y – 0 = – 1 (x – 0) or, x + y = 0
Let P(x, y) be any point on the parabola. Then,
Distance of P from the focus S
= Distance of P from the directrix x + y = 0   

⇒ 2x² + 2y² – 4x – 4y + 4 = x² + y2 + 2xy
⇒ x² + y² – 2xy – 4x – 4y + 4 = 0, which is the required equation of the parabola.

Question. If P is any point on a hyperbola and N is the foot of the perpendicular from P on the transverse axis, then prove that (PN)2/(AN)(A’N) = b²/a² .
Answer: Let P (a, b) be any point on hyperbola     

Question. If e and e′ be the eccentricities of a hyperbola and its conjugate, then prove that 1/e2 + 1/e’2 = 1 .
Answer: Let the equation of the hyperbola be
x²/a² – y²/b² = 1
Then, the equation of the hyperbola conjugate to (i) is
x²/a² – y²/b² = -1
We have, e = Eccentricity of (i)   

Question. Find the equation of the circle which passes through the centre of the circle x2 + y2 + 8x + 10y – 7 = 0 and is concentric with the circle 2×2 + 2y2 – 8x – 12y – 9 = 0.
Answer: We have to find the equation of circle (C2) which
passes through the centre of circle (C1) and is concentric
with circle (C3).
x2 + y2 + 8x + 10y – 7 = 0   

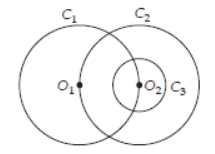
∴ Centre of C1 is O1 = (–4, –5)
Now, equation of circle (C2) which is concentric with
given circle (C3) 2×2 + 2y2 – 8x – 12y – 9 = 0 is
2×2 + 2y2 – 8x – 12y + k = 0 …(ii)
Since, circle (C2) passes through O1 (–4, –5).
∴ 2(–4)2 + 2(–5)2 –8(–4) – 12(–5) + k = 0
⇒ 32 + 50 + 32 + 60 + k = 0 ⇒ k = –174
On putting the value of k in (ii), we get
2×2 + 2y2 – 8x – 12y – 174 = 0
⇒ x2 + y2 – 4x – 6y – 87 = 0 which is required equation of circle (C2).

Question. Find the vertex, focus, directrix, axis and latus-rectum of the parabola y2 = 4x + 4y.
Answer: The given equation is y2 = 4x + 4y
⇒ y2 – 4y = 4x
⇒ y2 – 4y + 4 = 4x + 4
⇒ (y – 2)2 = 4(x + 1) …(i)
Shifting the origin to the point (–1, 2) without rotating
the axes and denoting the new coordinates with respect
to these axes by X and Y, we have,
x = X + (–1), y = Y + 2 …(ii)
Using these relations, (i) reduces to
Y2 = 4X
This is of the form Y2 = 4 aX.
On comparing we get 4a = 4 ⇒ a = 1.
Vertex: The coordinates of the vertex w.r.t. new axes
are (X = 0, Y = 0).
The coordinates of the vertex w.r.t. old axes are (–1, 2)
[Putting X = 0, Y = 0 in (ii)]
Focus: The coordinates of the focus w.r.t. new axes are (1, 0).
So, coordinates of the focus w.r.t. old axes are (0, 2)
[Putting X = 1, Y = 0 in (ii)]
Directrix: Equation of the directrix of the parabola w.r.t.
new axes is X = – 1
So, equation of the directrix of the parabola w.r.t. old axes is x = – 2.
Axis : Equation of axis of the parabola w.r.t. new axes is Y =0
So, equation of axis w.r.t. old axes is y = 2
[Putting Y = 0 in (ii)]
Latus rectum: The length of the latus rectum = 4.

Case Based Questions :

Case I : Read the following passage and answer the questions from 41 to 45.
Arun was playing a football match. When he kicked the football, the path formed by the football from ground level is parabolic, which is shown in the following graph. Consider the coordinates of point A as (3, –2).   

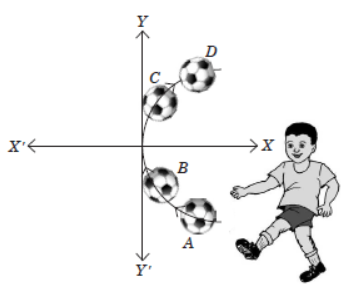
Question. The extremities of latus rectum of given curve are 
(a) (1/3 , ± 2/3)
(b) (2/3 , ± 1/3)
(c) (± 1/3 , 1)
(d) (± 1/3 , 4/3)

Question. The length of latus rectum of given curve is 
(a) 2/3
(b) 5/3
(c) 3
(d) 4/3

Question. Which of the following point lies on the path formed by football? 
(a) (–2, 0)
(b) (1,3/4)
(c) (-1/3 , 4)
(d) (3/4 , 1)

Question. The equation of path formed by the football is 
(a) y² = x + 1
(b) 3x² = 4y
(c) 3y² = 4x
(d) x² = y – 1

Question. The equation of directrix of path formed by football is 
(a) x − 4/3 = 0
(b) x + 2/3 = 0
(c) x + 3 = 0
(d) x + 1/3 = 0

Case II : Read the following passage and answer the questions from 46 to 50.
In maths period, Ananya studied about the ellipse. On the same day, her Physics teacher was exploring the rotation of Earth around the Sun, where the Sun is situated at one of the foci
of ellipse formed by Earth. Consider the path covered by Earth is represented by equation x²/169 + y²/144 = 1 .

Question. The eccentricity of the given curve is 
(a) 13/5
(b) 12/13
(c) 4/13
(d) 5/13

Question. The sum of focal radii of given curve is 
(a) 36
(b) 24
(c) 26
(d) 16

Question. Which of the following point lies on the curve formed by Earth around the Sun? 
(a) (–13, 14)
(b) (0, –12)
(c) (12, 0)
(d) (12, –13)

Question. Equation of directrices of given curve are 
(a) y = ± 144/169
(b) y = ± 169/5
(c) x = ± 5/169
(d) x = ± 169/5

Question. The vertices of the path covered by Earth around Sun is 
(a) (± 5, 0)
(b) (±13, 0)
(c) (0, ± 13)
(d) (0, ± 12)

Case III : Read the following passage and answer the questions from 51 to 55.
Karan, the student of class XI was studying in his house. He felt hungry and found that his mother was not at home. So, he went to the nearby shop and purchased a packet of chips.
While eating the chips, he observed that one piece of the chips is in the shape of hyperbola.
Consider the vertices of hyperbola at (±5, 0) and foci at (±7, 0). 

Question. What is the length of latus rectum of given hyperbolic curve?   
(a) 9.6
(b) 4.8
(c) 10.9
(d) 5.4

Question. The equation of directrices of given hyperbolic curve are 
(a) y = ± 7/25
(b) x = ± 24/7
(c) x = ± 25/7
(d) y = ± 12/25

Question. The equation of hyperbolic curve formed by given piece of chips is 
(a) x²/15 – y²/16 = 1
(b) x²/25 – y²/24 = 1
(c) x²/24 – y²/16 = 1
(d) x²/25 – y²/9 = 1

Question. The length of conjugate axis of given curve formed by given piece of chips is 
(a) 25
(b) 8 6
(c) 10
(d) 4 6

Question. The eccentricity of hyperbolic curve formed by given piece of chips is 
(a) 6/5
(b) -7/5
(c) 7/5
(d) -6/5