Please refer to MCQ Questions Chapter 2 Relations and Functions Class 11 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 11 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 11 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 2 Relations and Functions in Class 11 Mathematics provided below to get more marks in exams.
Chapter 2 Relations and Functions MCQ Questions
Please refer to the following Chapter 2 Relations and Functions MCQ Questions Class 11 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 2 Relations and Functions Class 11 Mathematics
Question. If A = {8, 9, 10} and B = {1, 2, 3, 4, 5}, then the number of elements in A × A × B are
(a) 15
(b) 30
(c) 45
(d) 75
Answer
C
Question. The graph of the function f : R → R and f(x) = x2 , x ∈ R, is

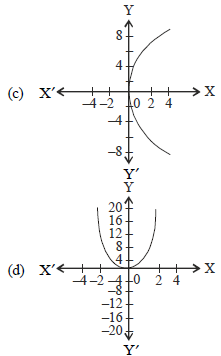
Answer
D
Question. If A = {1, 2}, B = {1, 3}, then (A × B) ∪ (B × A) is equal to
(a) {(1, 3), (2, 3), (3, 1), (3, 2), (1, 1), (2, 1), (1, 2)}
(b) {(1, 3), (3, 1), (3, 2), (2, 3)}
(c) {(1, 3), (2, 3), (3, 1), (3, 2), (1, 1)}
(d) None of these
Answer
A
Question. If f (x) = ax + b, where a and b are integers, f(–1) = –5 and f(3) = 3, then the value of ‘a’ is
(a) 3
(b) 0
(c) 2
(d) 1
Answer
C
Question. If the set A has 3 elements and the set B = {3, 4}, then the number of elements in A x B is
(a) 6
(b) 9
(c) 8
(d) 2
Answer
A
Question. Let A = {x, y, z} and B = {a, b, c, d}. Which one of the following is not a relation from A to B?
(a) {(x, a), (x, c)}
(b) {(y, c), (y, d)}
(c) {(z, a), (z, d)}
(d) {(z, b), (y, b), (a, d)}
Answer
D
Question. If the set A has p elements, B has q elements, then the number of elements in A × B is
(a) p + q
(b) p + q + 1
(c) pq
(d) p2
Answer
C
Question. The domain of the function f(x) = |x + 3|/x + 3 is
(a) {–3}
(b) R – {–3}
(c) R – {3}
(d) R
Answer
B
Question. Domain of √a2 – x2 , (a > 0) is
(a) (–a, a)
(b) [–a, a]
(c) [0, a]
(d) (–a, 0]
Answer
B
Question. If f(x) = x/x–1 , then f (a)/f (a+1) is equal to:
(a) f(a2)
(b) f (1/a)
(c) f(– a)
(d) f(– a/a–1)
Answer
A
Question. If g(x) = 1 +√x and f [g (x)] = 3 + 2√x + x , then f(x) =
(a) 1 + 2x2
(b) 2 + x2
(c) 1 + x
(d) 2 + x
Answer
B
Question. Let n(A) = 8 and n(B) = p. Then, the total number of non-empty relations that can be defined from A to B is
(a) 8p
(b) np – 1
(c) 8p – 1
(d) 28p – 1
Answer
D
Question. If f is the identity function and g is the modulus function, then match the column-I with column-II.

Codes:
A B C D
(a) 1 4 3 2
(b) 4 1 2 3
(c) 4 1 3 2
(d) 2 1 3 4
Answer
B
Question. If (x + 3, 4 – y) = (1, 7), then the value of 4 + y is
(a) 3
(b) 4
(c) 5
(d) 1
Answer
D
Question. The domain of relation
R = {(x, y) : x2 + y2 = 16, x, y ∈ Z} is
(a) {0, 1, 2, 3, 4}
(b) {–4, –3, –2, –1}
(c) {–4, –3, –2, –1, 0, 1, 2, 3, 4}
(d) None of the above
Answer
D
Question. If A, B and C are three sets, then
(a) A × (B ∩ C) = (A × B) ∩ (A × C)
(b) A × (B’ ∪ C’) = (A × B) ∩ (A × C)
(c) Both (a) and (b)
(d) None of the above
Answer
C
Question. If A = {1, 2, 4}, B = {2, 4, 5}, C = {2, 5}, then (A – C) × (B – C) is equal to
(a) {(1, 4)}
(b) {(1, 4), (4, 4)}
(c) {(4, 1), (4, 4)}
(d) {(1, 2), (2, 5)}
Answer
B
Question. The domain of the function f defined by f(x) = 1/√x – |x| is
(a) R
(b) R+
(c) R–
(d) {Φ}
Answer
D
Question. The relation R defined on set A = {x : |x| < 3, x ∈ I} by
R = {(x, y) : y = |x|} is
(a) {(–2, 2), (–1, 1), (0, 0), (1, 1), (2, 2)}
(b) {(–2, –2), (–2, 2), (–1, 1), (0, 0), (1, –2), (1, 2), (2, –1), (2, –2)}
(c) {(0, 0), (1, 1), (2, 2)}
(d) None of these
Answer
A
Question. If f (x + 1) = x2 – 3x + 2, then f (x) is equal to:
(a) x2 – 5x – 6
(b) x2 + 5x – 6
(c) x2 + 5x + 6
(d) x2 – 5x + 6
Answer
D
Question. Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a linear function from Z into Z, then f(x) =
(a) 2x – 1
(b) 2x
(c) 2x + 1
(d) –2x + 1
Answer
A
Question. Let A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}. Then, match the following in column-I with the sets of ordered pairs in column-II.

Codes:
A B C D E
(a) 1 2 1 2 3
(b) 2 2 1 1 3
(c) 1 1 2 2 3
(d) 2 1 2 3 2
Answer
C
Question. The number of elements in the set {(x, y) : 2x2 + 3y2 = 35, x, y ∈ Z}, where Z is the set of all integers,
(a) 8
(b) 2
(c) 4
(d) 6
Answer
A
Question. A relation is represented by
(a) Roster method
(b) Set-builder method
(c) Both (a) and (b)
(d) None of these
Answer
C
Question. If g = {(1, 1), (2, 3), (3, 5), (4, 7)} is a function described by the formula, g (x) = αx + β then what values should be assigned to α and β?
(a) α = 1, β= 1
(b) α = 2, β = – 1
(c) α = 1, β = – 2
(d) α = – 2, β = – 1
Answer
B
Question. The domain of the real valued function
f(x) = √5 – 4x – x2 + x2 log(x + 4) is
(a) (– 5, 1) (b) – 5 ≤ x and x ≥ 1
(c) (– 4, 1)
(d) Φ
Answer
C
Question.
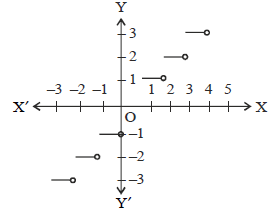
f(x) = [x]
Which of the following options identify the above graph?
(a) Modulus function
(b) Greatest integer function
(c) Signum function
(d) None of these
Answer
B
Question. If A is the set of even natural numbers less than 8 and B is the set of prime numbers less than 7, then the number of relations from A to B is
(a) 29
(b) 92
(c) 32
(d) 29 – 1
Answer
A
Question. The domain of the function
f(x) = 3/4 – x2 + log10 (x3 – x), is
(a) (– 1, 0) ∪ (1, 2)
(b) (1, 2) ∪ (2, ∞)
(c) (– 1, 0) ∪ (1, 2) ∪ (2, ∞)
(d) (1, 2)
Answer
C
Question. If A, B and C are any three sets, then A × (B ∪ C) is equal to
(a) (A × B) ∪ (A × C)
(b) (A ∪ B) × (A ∪ C)
(c) (A × B) ∩ (A × C)
(d) None of these
Answer
A
Question. The Cartesian product of two sets P and Q, i.e., P × Q = Φ, if
(a) either P or Q is the null set
(b) neither P nor Q is the null set
(c) Both (a) and (b)
(d) None of the above
Answer
A
Question. If P = {a, b, c} and Q = {r}, then
(a) P × Q = Q × P
(b) P × Q ≠ Q × P
(c) P × Q ⊂ Q × P
(d) None of these
Answer
B
Question. Let f(x) = x2 and g(x) = 2x + 1 be two real functions. Then, match the functions given in column-I with the expressions in column-II.

Codes:
A B C D
(a) 2 1 4 3
(b) 4 1 2 3
(c) 2 1 3 4
(d) 2 4 1 3
Answer
A
Question. If f (x) = 4x– x2 , x ∈ R, then f (b + 1) – f (b – 1) is equal to m (2 – b). The value of ‘m’ is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
C
STATEMENT TYPE QUESTIONS
Question. Consider the following statements:
Statement-I: The domain of the relation
R = {(a, b) : a ∈ N, a < 5, b = 4} is {1, 2, 3, 4}.
Statement-II: The range of the relation
S = {(a, b) : b = |a – 1|, a ∈ Z and |a| ≤ 3} is {1, 2, 3, 4}.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
A
Question. Consider the following statements.
I. Relation R = {(2, 0), (4, 8), (2, 1), (3, 6)} is not a function.
II. If first element of each ordered pair is different with other, then the given relation is a function.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both I and II are true.
(d) Neither I nor II is true.
Answer
C
Question. Consider the following statements.
I. Let A and B are non-empty sets such that A ⊆ B. Then, A x C ⊆ B x C.
II. For any two sets A and B, A x B = B x A
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
A
Question. Consider the following statements:
Statement-I: The Cartesian product of two non-empty sets P and Q is denoted as P × Q and P × Q = {(p, q) : p ∈ P, q ∈ Q}.
Statement-II: If A = {red, blue} and B = {b, c, s}, then A × B = {(red, b), (red, c), (red, s), (blue, b), (blue, c), (blue, s)}.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
C
Question. Consider the following statements
I. Let n(A) = m and n(B) = n. Then the total number of non-empty relations that can be defined from A to B is 2mn – 1
II. If A = {1, 2, 3}, B = {3, 8}, then (A ∪ B) x (A ∩ B) is equal to {(1, 3), (2, 3), (3, 3), (8, 3)}.
III. If (x/2 – 1, y/9 + 1)= (2, 1), then the values of x and y respectively are 6 and 0.
Choose the correct option.
(a) Only I and II are false.
(b) Only II and III are true.
(c) Only I and III are true.
(d) All the three statements are true
Answer
D
Question. The figure given below shows a relation R between the sets A and B.
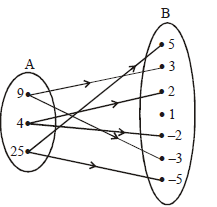
Then which of the following is correct?
I. The relation R in set-builder form is {(x,y) : x is the square of y, x ∈ A, y ∈ B}
II. The domain of the relation R is {4, 9, 25}
III. The range of the relation R is {–5, –3, –2, 2, 3, 5}
(a) Only I and II are true.
(b) Only II and III are true.
(c) I, II and III are true
(d) Neither I, II nor III are true.
Answer
C
Question. Consider the following statements:
Statement-I: If R is a relation from A to B, then domain of R is the set A.
Statement-II: The set of all second elements in a relation R from a set A to a set B is called co-domain of R.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
D
Question. Consider the following statements.
I. If (a, 1), (b, 2) and (c, 1) are in A x B and n(A) = 3, n (B) = 2, then A = {a, b, c} and B = {1, 2}
II. If A = {1, 2} and B = {3, 4}, then A x (B ∩ Φ) is equal to A x B.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Neither I nor II is true
Answer
A


