Case Study Chapter 6 Triangles Mathematics

Please refer to Case Study Chapter 6 Triangles Mathematics with answers provided below. These case study based questions are expected to come in the upcoming Class 10 Mathematics examinations. We have provided case study questions class 10 maths for all chapters on our website as per the latest examination pattern issued by CBSE, NCERT, and KVS.

Chapter 6 Triangles Case study Questions Class 10 Maths

I. Scale Factor and Similarity Scale Factor
A scale drawing of an object is the same shape as the object but a different size. The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as a ratio.
Similar Figures

The ratio of two corresponding sides in similar figures is called the scale factor.
Scale factor = Length in image / Corresponding length in object
If one shape can become another using resizing, then the shapes are similar.

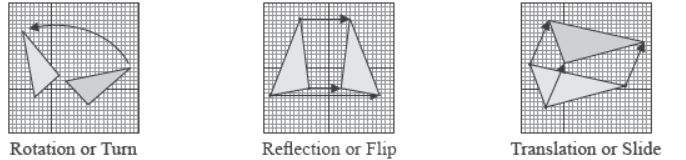
Hence, two shapes are similar when one can become the other after a resize, flip, slide or turn.

Question. If two similar triangles have a scale factor of a : b, which statement regarding the two triangles is true?   
(a) The ratio of their perimeters is 3a : b
(b) Their altitudes have a ratio a : b
(c) Their medians have a ratio a/2 : b
(d) Their angle bisectors have a ratio a² : b²

Question. The shadow of a stick 5 m long is 2 m. At the same time, the shadow of a tree 12.5 m high is   
(a) 3 m
(b) 3.5 m
(c) 4.5 m
(d) 5 m

Question. What will effect the similarity of any two polygons?   
(a) They are flipped horizontally.
(b) They are dilated by a scale factor.
(c) They are translated down.
(d) They are not the mirror image of one another.

Question. Below you see a student’s mathematical model of a farmhouse roof with measurements. The attic floor, ABCD in the model, is a square. The beams that support the roof are the edges of a rectangular prism, EFGHKLMN. E is the middle of AT, F is the middle of BT, G is the middle of CT, and H is the middle of DT. All the edges of the pyramid in the model have length of 12 m. What is the length of EF, where EF is one of the horizontal edges of the block?   
(a) 24 m
(b) 3 m
(c) 6 m
(d) 10 m

Question. A model of a boat is made on the scale of 1 : 4. The model is 120 cm long. The full size of the boat has a width of 60 cm. What is the width of the scale model ?   
(a) 20 cm
(b) 25 cm
(c) 15 cm
(d) 240 cm

II. Kerala
Kerala is a state in Southern India. The state is known as a tropical paradise of waving palms and wide sandy beaches. This map of the Indian province of Kerala shows its area that can be approximated using a simple straight-sided shape. The shape has two parallel sides 561 km and 216 km long. The other sides are 180 km and 211 km long. Its parallel sides are 100 km apart. Shreya observed the shape formed by four straight lines and explored it on her notebook in different ways shown below.

Question. Again AB || CD. If DO = 3x – 1, OB = 5x – 3, AO = 6x – 5 and OC = 2x + 1, then the value of x is   
(a) 0
(b) 1
(c) 2
(d) 3

Question. In ΔABC, PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, AB and PQ are respectively     
(a) AB = 6 cm, PQ = 2.4 cm
(b) AB = 4.8 cm, PQ = 8.2 cm
(c) AB = 4 cm, PQ = 5.3 cm
(d) AB = 8.4 cm, PQ = 2.8 cm

Question. Let ABCD is a trapezium with AB || DC, E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Then AE ED =   
(a) BF/ CD
(b) AB/ CD
(c) BF/ FC
(d) None of these.

Question. In ΔDEF, if RS || EF, DR = 4x – 3, DS = 8x – 7, ER = 3x – 1 and FS = 5x – 3, then the value of x is   
(a) 1
(b) 2
(c) 8
(d) 10

Question. Here, AB || CD. If DO = 3x – 19, OB = x – 5, CO = x – 3 and AO = 3, the value of x is   
(a) 5 or 8
(b) 8 or 9
(c) 10 or 12
(d) None of these.

III . A Frame House: A frame-house is a house constructed from a wooden skeleton, typically covered with timber board. The concept of similar triangles is used to construct it. Look at the following picture:

Question. Again consider the front view of house (ii). If S and T are points on side PQ and PR respectively such that ST || QR and PS : SQ = 3 : 1. Also TP = 6.6 m, then PR is   

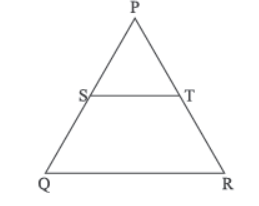
(a) 6.9 m
(b) 8.8 m
(c) 10.5 m
(d) 9.4 m

Question. The front view of house (i) is shown along side in which point P on AB is joined with point Q on AC.     
If PQ || BC, AP = x m, PB = 10 m, AQ = (x – 2) m, QC = 6 m, then the value of x is   

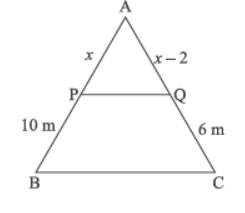
(a) 3 m
(b) 4 m
(c) 5 m
(d) 8 m

Question. The side view of house (i) is shown below in which point F on AC is joined with point G on DE. If ACED is a trapezium with AD || CE, F and G are points on nonparallel sides AC and DE respectively such that FG is parallel to AD, then AF/ FC =   

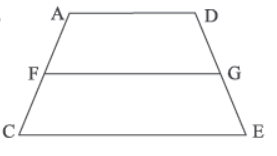
(a) DG/ GE
(b) AD /CE
(c) AF/ GE 
(d) DG/ FC 

Question. Sneha has also a frame house whose front view is shown below If MN || AB, BC = 7.5 m, AM = 4 m and MC = 2 m, then length of BN is 

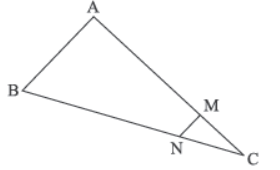
(a) 5 m
(b) 4 m
(c) 8 m
(d) 9 m

Question. The front view of house (ii) is shown along side in which point S on PQ is joined with point T on PR. If PS/ QS =  PT/ TR = and ∠PST = 70°, ∠QPR = 50°, then angle  ∠QRP = 

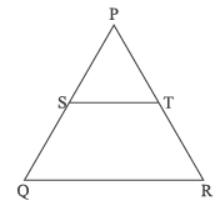
(a) 70°
(b) 50°
(c) 80°
(d) 60°

IV. Star of David: The six-pointed Star of David is a common symbol for Judaism. Known in Hebrew as a Magen David (shield of David), geometrically it has two equilateral triangles superimposed on each other. The diagram representing the Star of David can be shown as below:

Question. If the median of equilateral triangle ΔABC is √3 cm, then the length of side of equilateral triangle is   
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm

Question. If in two triangles ABC and PQR, AB/ QR = BC/ PR = CA /PQ  , then   
(a) ΔPQR ~ ΔCAB
(b) ΔPQR ~ ΔABC
(c) ΔCBA ~ ΔPQR
(d) ΔBCA ~ ΔPQR

Question. Ayush has drawn a triangle DEF similar to ΔABC in his notebook such that the perimeters of ΔABC and ΔDEF are representing 27 cm and 15 cm. If one side of the first triangle is 9 cm, then the corresponding side of second triangle is   
(a) 4.5 cm
(b) 5 cm
(c) 6 cm
(d) None of these.

Question. If the side of equilateral triangle PQR is 3√3 cm, then the length of the altitude is   
(a) 3 cm
(b) 4 cm
(c) 4.5 cm
(d) 5 cm

Question. In triangle PQR, from S and T, altitudes TQ and SR are drawn. Which of the following is true? 

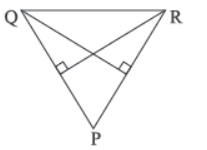
(a) ΔRSP ~ ΔQTP
(b) ΔRSQ ~ ΔRTQ
(c) ΔRSQ ~ ΔRSP
(d) None of these.

V. Rahul is studying in X Standard. He is making a kite to fly it on a Sunday. Few questions came to his mind while making the kite. Give answers to his questions by looking at the figure.

Question. Sides of two similar triangles are in the ratio 4:9. Corresponding medians of these triangles are in the ratio    
(a) 2:3
(b) 4:9
(c) 81:16
(d) 16:81

Question. In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle. This theorem is called as, 
(a) Pythagoras theorem
(b) Thales theorem
(c) Converse of Thales theorem
(d) Converse of Pythagoras theorem

Question. Rahul tied the sticks at what angles to each other?     
(a) 30°
(b) 45°
(c) 90°
(d) 60°

Question. Which is the correct similarity criteria applicable for smaller triangles at the upper part of this kite?   
(a) RHS
(b) SAS
(c) SSA
(d) AAS

Question. What is the area of the kite, formed by two perpendicular sticks of length 6 cm and 8 cm?   
(a) 48 cm²
(b) 14 cm²
(c) 24 cm²
(d) 96 cm²

VI. Rohan wants to measure the distance of a pond during the visit to his native. He marks points A and B on the opposite edges of a pond as shown in the figure below. To find the distance between the points, he makes a right-angled triangle using rope connecting B with another point C at a distance of 12 m, connecting C to point D at a distance of 40 m from point C and connecting D to the point at A which is at a distance of 30 m from D such that ADC = 90º

Question. Which is the following does not form a Pythagoras triplet?     
(a) (7, 24, 25)
(b) (15, 8, 17)
(c) (5, 12, 13)
(d) (21, 20, 28)

Question. The length of AB is   
(a) 12 m
(b) 38 m
(c) 50 m
(d) 100 m

Question. Which property of geometry will be used to find the distance AC?   
(a) Similarity of triangles
(b) Thales Theorem
(c) Pythagoras Theorem
(d) Congruency of triangles

Question. The length of the rope used the     
(a) 120 m
(b) 70 m
(c) 82 m
(d) 22 m

Question. What is the distance AC?   
(a) 50 m
(b) 12 m
(c) 100 m
(d) 70 m

We hope you liked the above provided Case Study Chapter 6 Triangles Mathematics case study questions class 10 maths provided above. Please let us know in the comments box below if you have any questions.