Please refer to Assignments Class 10 Mathematics Quadratic Equation Chapter 4 with solved questions and answers. We have provided Class 10 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 4 Quadratic Equation Class 10 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Quadratic Equation Assignments Class 10 Mathematics
VERY SHORT ANSWER TYPE QUESTIONS
Question. Which of the following equation has 2 as a root
(a) x2 + 4 = 0
(b) x2 – 4 = 0
(c) x2 + 3x – 12 = 0
(d) 3x2 – 6x – 2 = 0
Ans. (b) x2 – 4 = 0
Question. The value(s) of k for which the quadratic equation 2x2 + kx + 2 = 0 has equal roots, is
(a) 4
(b) ± 4
(c) – 4
(d) 0
Ans. (b) ± 4
Question. Every Quadratic Equation can have at most
(a) Three roots
(b) One root
(c) Two roots
(d) Any number of roots
Ans. (c) Two roots
Question. The qaudratic equation x2 – 5x – 6 = 0 if expressed as (x + p) (x + q) = 0 then value of p and q respectively are ______ and _______ .
Ans. p = – 6, q = 1 [x2 – 5x – 6 = 0 ⇒ (x – 6) (x + 1) = 0]
Question. If roots of 4x2 – 2x + c = 0 are reciprocal of each other then the value of c is ________ .
Ans. c = 4 (∵ product = 1 ⇒ c/a = 1 ⇒ c/4 = 1 )
Question. The graph of a quadratic polynomial is a straight line. True or False
Ans. False (Degree of quadratic polynomial is 2 not 1 ∵ Not a straight line)
Question. If the coefficient of x2 and the constant term of a quadratic equation have opposite signs, then the quadratic equation has real roots. True or False
Ans. True (Coefficient of x2 = a, Constant = – c, D = b2 – 4ac = b2 – 4(a) (– c) = b2 + 4ac > 0)
Question. Match the following :
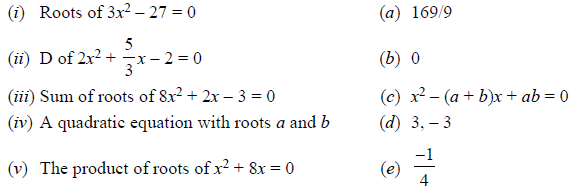
Ans. (i) → d, (ii) → a, (iii) → e
(iv) → c, (v) → b
SHORT ANSWER TYPE QUESTIONS-I
Question. Solve for x by factorisation (x – 1)2 – 5(x – 1) – 6 = 0
Ans. Take (x-1) = y
y2 – 5y – 6 = 0 ⇒ (y + 1) (y – 6) = 0
y = –1, y = 6
x – 1 = – 1, x – 1 = 6
x = 0, x = 7
Question. For what vlaue of ‘a’ quadratic equation 3ax2 – 6x + 1 = 0 has no real roots?
Ans. D < 0, (– 6)2 – 4(3a) (1) < 0, 12a > 36 ⇒ a > 3
Question. Solve for x by factorisation 8x2 – 22x – 21 = 0
Ans. x = 7/2, x = 3/4
Question. If x = 2/3 and x = – 3 are roots of the quadratic equation ax2 + 7x + b = 0. Find the value of a and b.
Ans. Substituting, x = 2/3 we get
4a + 9b = – 42 …(1)
Substituting, x = – 3 we get
9a + b = 21 …(2)
Solve (1) and (2) to get a = 3, b = – 6.
Question. Solve for x by factorisation √3x2 + 10x + 7√3 = 0
Ans. x = -√3, x = (-7√3)/3
Question. Find value of p for which the product of roots of the quadratic equation px2 + 6x + 4p = 0 is equal to the sum of the roots.
Ans. Product = c/a = 4p/p = 4, sum = -b/a = -6/p
ATQ = -6/p = 4 ⇒ p = -6/4 = -3/2
Question. Solve for x by factorisation √2x2 + 7x + 5√2 = 0
Ans. x = -√2, x = (-5√2)/2
SHORT ANSWER TYPE QUESTIONS-II
Question. Solve for x
x-4/x-5 + x-6/x-7 = 10/3, x ≠ 5, 7
Ans. Take LCM to get 2x2 – 27x + 88 = 0
x = 8, 11/2
Question. Solve for x
(2x/x-5)2 + 10x/(x-5) – 24 = 0, x ≠ 5
Ans.
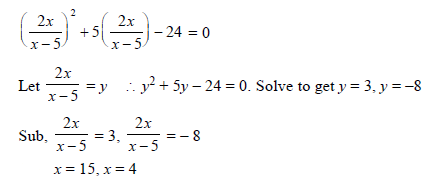
Question. Solve for x
1/(x+1) + 2/(x+2) = 4/(x+4), x ≠ -1, -2, -4
Ans. Take LCM to get x2 – 4x – 8 = 0 (Use quadratic formula)
x = 2±2√3
Question. Solve 9x2 – 6a2x + a4 – b4 = 0 using quadratic formula.
Ans.
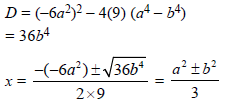
Question. Solve for x
1/(2x-3) + 1/(x-5) = 1, x ≠ 3/2, 5
Ans. Take LCM to get 2x2 – 16x + 23 = 0
Solve using Quadratic formula
x = (-8±3√2)/2
Question. Solve for x
16/x – 1= 15/(x+1), x ≠ 0, -1
Ans. (16-x)/x = 15/(x+1)
x2 – 16 = 0
x = ± 4
Question. Solve by using quadratic formula abx2 + (b2 – ac) x – bc = 0.
Ans.

Question. Solve for x
2a2x2 + b(6a2 + 1)x + 3b2 = 0
Ans.

Question. Solve for x
1/(a + b + x) = 1/a + 1/b + 1/x
a + b + x ≠ 0, a, b, x ≠ 0
Ans.

Question. Find the nature of roots of the quadratic equation 3x2 – 4√3 x + 4 = 0 If the roots are real, find them.
Ans.

Question. Solve for x
2/(x+1) + 3/(2(x-2) = 23/5x , x ≠ 0, -1, 2
Ans.
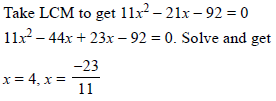
LONG ANSWER TYPE QUESTIONS
Question. The speed of a boat in still water is 15 km/hr. It can go 30 km upstream and return downstream to the orignal point in 4 hrs 30 minutes. Find the speed of the stream.
Ans. ATQ 30/(15-x) + 30/(15+x) = 9/2, (Speed of stream x km/hr)
Solve to get x = 5, x =–5 (rejected)
∴ Answer is 5 km/hr
Question. The area of an isosceles triangle is 60 cm2. The length of equal sides is 13 cm find length of its base.
Ans.
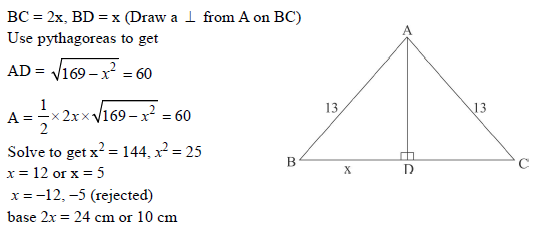
Question. A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policemen will catch the thief?
Ans. Let time taken by thief be n minutes.
Policeman will catch the thief in (n – 1) minutes.
Total distance covered by thief = (100 n) metres …(1)
(as distance covered in 1 min = 100 min)
Distance covered by policemen
100 + 110 + 120 + …. + to (n – 1) 10 …(2)
(1) and (2) ⇒ 100 n =(n-1)/2 [2 × 100 + (n – 2) 10]
Solve and get n2 – 3n – 18 = 0
n = 6, n ≠ – 3
Policeman will catch the thief in 5 minutes.
Question. A girl is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages.
Ans. Age of sister = x years
Age of girl = 2x
ATQ (x + 4) (2x + 4) = 160
Solve to get x2 + 6x – 72 = 0
x = 6 years, x = – 12 (rejected)
2x = 12 years
Question. A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m. Find the length and breadth of the park.
Ans. Let Lm be the length of the rectangular park
Breadth = (L – 3) m
Altitude of the isosceles triangle = 12 m
ATQ L(L – 3) = 1/2 (12) (L – 3) + 4
L2 – 9L + 14 = 0
(L – 7) (L – 2) = 0
⇒ L = 7, 2
So, L = 7m (L = 2 rejected ∵ L – 3 = –1)
∵ Length = 7 m, Breadth = 4 m
Question. A two digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.
Ans. Let tens place digit = x, then units digits = 18/x.
No, 10x + 18/x
ATQ (10x + 18/x) – ((10×18)/x)+x) = 63
Solve to get x = 9, x ≠ – 2 (rejected).
∴ Answer is Number is 92
Question. In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed, so that the area of the grass surrounding the pond would be 1184 m2. Find the lenght and breadth of the pond.
Ans.
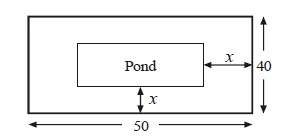
Length of rectangular lawn = 50 m
Breadth of rectangular lawn = 40 m
Length of pond = 50 – 2x
Breadth of pond = 40 – 2x
Area of lawn – Area of pond = area of grass
50 × 40 – (50 – 2x) (40 – 2x) = 1184
get x2 – 45x + 296 = 0
x = 37, x = 8
x = 37 rejected ∵ 40 – 2x = 40 – 2(37) < 0
Length of pond = 34 m
Breadth of pond = 24 m
Question. Three consecutive positive integers are such that the sum of the square of the first and the product of other two is 46, find the integers.
Ans.
Question. If the equation (1 + m2)n2x2 + 2mncx + (c2 – a2) = 0 has equal roots, prove that c2 = a2 (1 + m2).
Ans.

Question. A piece of cloth costs ₹ 200. If the piece was 5 m longer and each metre of cloth costs ₹ 2 less, then the cost of the piece would have remained unchanged. How long is the piece and what is the original rate per metre?
Ans.

Question. In a flight of 600 km, an aircraft was slowed down due to bad weather. Its average speed was reduced by 200 km/hr and the time of flight increased by 30 minutes. Find the duration of flight.
Ans. ATQ 600/(x-200) – 600/x = 1/2, [Speed of aircraft = x km/hr]
Solve to get x = 600, x ≠ – 400
Duration of flight 600/600 = 1hr.
Question. A peacock is sitting on the top of a pillar, which is 9 m high. From a point 27 m away from the bottom fo a pilar, a snake is coming to its hole at the base of the pillar. Seeing the snake the peacock pounces on it. If their speeds are equa, at what distance from the hole is the snake caught?
Ans.
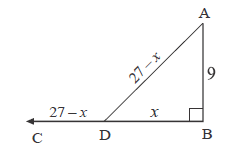
In ΔABD, pythagoras theorem 92 + x2 = (27 – x)2. Solve it to get x = 12 m.
