Please refer to Assignments Class 11 Mathematics Linear Inequalities Chapter 6 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 6 Linear Inequalities Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Linear Inequalities Assignments Class 11 Mathematics
Question. If |x + 2| ≤ 9, then
(a) x ∈ (–7, 11)
(b) x ∈ [–11, 7]
(c) x ∈ (–∞, –7) ∪ (11, ∞)
(d) x ∈ (–∞, –7) ∪ [11, ∞)
Answer
B
Question. The solution set of the inequality 4x + 3 < 6x + 7 is (–a, ∞). The value of ‘a’ is
(a) 1
(b) 4
(c) 2
(d) None of these
Answer
C
Question. The set of values of x satisfying 2 ≤ |x – 3| < 4 is
(a) (–1, 1] ∪ [5, 7)
(b) –4 ≤ x ≤ 2
(c) –1 < x < 7 or x ≥ 5
(d) x < 7 or x ≥ 5
Answer
A
Question. If x is real number and |x| < 3, then
(a) x ≥ 3
(b) –3 < x < 3
(c) x ≤ −3
(d) −3 ≤ x ≤ 3
Answer
B
Question. The set of real x satisfying the inequality 5 − 2x/3 ≤ x/6 −5 is [a, ∞). The value of ‘a’ is
(a) 2
(b) 4
(c) 6
(d) 8
Answer
D
Question. If –5 ≤ 5 – 3x/2 ≤ 8, then x ∈
(a) [–11/3 , 5]
(b) [–5, 5]
(c) [–11/3,∞)
(d) (–∞, ∞)
Answer
A
Question. The solution of the inequality –8 ≤ 5x – 3 < 7 is [–a, b). Sum of ‘a’ and ‘b’ is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
Question. A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and the third length is to be twice as long as the shortest. The possible length of the shortest board, if the third piece is to be at least 5 cm longer than the second, is
(a) less than 8 cm
(b) greater than or equal to 8 cm but less than or equal to 22 cm
(c) less than 22 cm
(d) greater than 22 cm
Answer
B
Question. Given that x, y and b are real numbers and x < y , b < 0, then
(a) x/b < y/b
(b) x/b ≤ y/b
(c) x/b > y/b
(d) x/b ≥ y/b
Answer
C
Question. Solutions of the inequalities comprising a system in variable x are represented on number lines as given below, then

(a) x ∈ (–∞, –4] ∪ [3, ∞)
(b) x ∈ [–3, 1]
(c) x ∈ (–∞, –4) ∪ [3, ∞)
(d) x ∈ [–4, 3]
Answer
A
Question. The length of a rectangle is three times the breadth. If the minimum perimeter of the rectangle is 160 cm, then
(a) breadth > 20 cm
(b) length < 20 cm
(c) breadth ≥ 20 cm
(d) length ≤ 20 cm
Answer
C
Question. The marks obtained by a student of class XI in first and second terminal examinations are 62 and 48, respectively. The minimum marks he should get in the annual examination to have an average of at least 60 marks, are
(a) 70
(b) 50
(c) 74
(d) 48
Answer
A
Question. Solution of (x – 1)2 (x + 4) < 0 is
(a) (–∞, 1)
(b) (–∞, –4)
(c) (–1, 4)
(d) (1, 4)
Answer
B
Question. The length of a rectangle is three times the breadth. If the minimum perimeter of the rectangle is 160 cm, then what can you say about breadth?
(a) breadth = 20
(b) breadth ≤ 20
(c) breadth ≥ 20
(d) breadth ≠ 20
Answer
C
Question. If 5x + 1 > –24 and 5x –1 < 24, then x ∈ (–a, a). The value of ‘a’ is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
D
Question. Solution of linear inequality in variable x is represented on number line is

(a) x ∈(9/2,∞)
(b) x ∈[9/2,∞)
(c) x ∈(−∞,9/2)
(d) x ∈(−∞,9/2]
Answer
B
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.
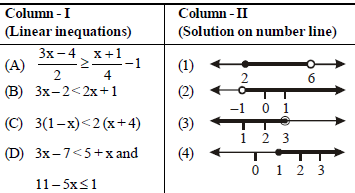
Codes
A B C D
(a) 4 2 3 1
(b) 1 3 2 4
(c) 4 3 2 1
(d) 1 2 3 4
Answer
C
Question. The pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23, are
(a) (4, 6), (6, 8), (8, 10), (10, 12)
(b) (6, 8), (8, 10), (10, 12)
(c) (6, 8), (8, 10), (10, 12), (12, 14)
(d) (8, 10), (10, 12)
Answer
B
Question. If |x| < 3 and x is a real number, then – m < x < m. The value of m is
(a) 3
(b) 4
(c) 2
(d) 1
Answer
A
Question. If |2x – 3 | < |x + 5|, then x belongs to
(a) (–3, 5)
(b) (5, 9)
(c) (– 2 /3, 8)
(d) (–8, 2/3)
Answer
C
Question. Solution of |x – 1| ≥ |x – 3| is
(a) x ≤ 2
(b) x ≥ 2
(c) [1, 3]
(d) None of these
Answer
B
Question. The solution set of the inequalities 6 ≤ –3(2x – 4) < 12 is
(a) (–∞, 1]
(b) (0, 1]
(c) (0, 1] ∪ [1, ∞)
(d) [1, ∞)
Answer
B
Question. Solution of |1+3/x| > 2 is
(a) (0, 3]
(b) [–1, 0)
(c) (–1, 0) ∪ (0, 3)
(d) None of these
Answer
C
Question. The number of pairs of consecutive odd natural numbers both of which are larger than 10, such that their sum is less than 40, is
(a) 4
(b) 6
(c) 3
(d) 8
Answer
A
Question. The solution set of the inequality 3(2 – x) ≥ 2(1 – x) is (–∞, a]. The value of ‘a’ is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
C
Question. Solution of |2x – 3| < |x + 2| is
(a) (–∞ , 1/3)
(b) (1/3 , 5)
(c) (5, ∞)
(d) (–∞ , 1/3) ∪ (5, ∞)
Answer
B
Question. The graphical solution of the inequalities x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0 is
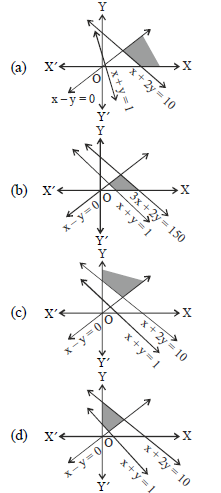
Answer
D
STATEMENT TYPE QUESTIONS
Question. I. When x is an integer, the solution set of 3x + 8 > 2 is {–1, 0, 1, 2, 3, …}.
II. When x is a real number, the solution set of 3x + 8 > 2 is {–1, 0, 1}.
Choose the correct option.
(a) Only I is incorrect.
(b) Only II is incorrect.
(c) Both I and II are incorrect.
(d) Both I and II are correct.
Answer
B
Question. Consider the following statements:
Statement-I : The solution set of 5x – 3 < 7, when x is an integer, is {….., –3, –2, –1}.
Statement-II : The solution of 5x – 3 < 7, when x is a real number, is (–∞, 2).
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
B
Question. Consider the following statements about Linear Inequalities :
I. Two real numbers or two algebraic expressions related by the symbols <, >, ≤ or ≥ form an inequality.
II. When equal numbers added to (or subtracted from) both sides of an inequality then the inequality does not changed.
III. When both sides of an inequality multiplied (or divided) by the same positive number then the inequality does not changed.
Which of the above statements are true ?
(a) Only I
(b) Only II
(c) Only III
(d) All of the above
Answer
D
Question. Consider the following statements:
Statement-I : The region containing all the solutions of an inequality is called the solution region.
Statement-II : The half plane represented by an inequality is checked by taking any point on the line.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
A
Question. Consider the following statements:
Statement-I : Consider the inequality 30x < 200 such that x is not a negative integer or fraction. Then, the value of x, which make the inequality a true statement are 1, 2, 3, 4, 5, 6.
Statement-II : The solution of an inequality in one variable is the value of that variable which makes it a true statement.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
B
Question. Which of the following linear inequalities satisfy the shaded region of the given figure.
I. x + 2y ≤ 8
II. x ≥ 0, y ≥ 0
III. x ≤ 0, y ≤ 0
IV. 2x + y ≤ 8
V. 4x + 5y ≤ 40
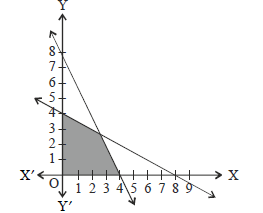
(a) I, III and V
(b) I, IV and V
(c) I, III and IV
(d) I, II, and IV
Answer
D
Question. Consider the following statements.
I. Inequalities involving the symbol ≥ or ≤ are called slack inequalities.
II. Inequalities which do not involve variables are called numerical inequalities.
Choose the correct option.
(a) Only I is true
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C

