Please refer to Assignments Class 11 Mathematics Permutations and Combinations Chapter 7 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 7 Permutations and Combinations Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Permutations and Combinations Assignments Class 11 Mathematics
Question. If 12Pr = 11P6 + 6. 11P5, then r is equal to:
(a) 6
(b) 5
(c) 7
(d) None of these
Answer
A
Question. At an election, a voter may vote for any number of candidates not greater than the number to be elected. There are 10 candidates and 4 are to be elected. If a voter votes for at least one candidate, then the number of ways in which he can vote, is
(a) 6210
(b) 385
(c) 1110
(d) 5040
Answer
B
Question. A boy has 3 library tickets and 8 books of his interest in the library. Of these 8, he does not want to borrow Mathematics Part II, unless Mathematics Part I is also borrowed. In how many ways can he choose the three books to be borrowed?
(a) 40
(b) 45
(c) 42
(d) 41
Answer
D
Question. Given 12 points in a plane, no three of which are collinear. Then number of line segments can be determined, are:
(a) 76
(b) 66
(c) 60
(d) 80
Answer
B
Question. 12 persons are to be arranged to a round table. If two particular persons among them are not to be side by side, the total number of arrangements is
(a) 9(10!)
(b) 2(10!)
(c) 45(8!)
(d) 10!
Answer
A
Question. Number of different ways in which 8 persons can stand in a row so that between two particular person A and B there are always two person is
(a) 11
(b) 13
(c) 15
(d) 16
Answer
D
Question. There are four chairs with two chairs in each row. In how many ways can four persons be seated on the chairs, so that no chair remains unoccupied ?
(a) 6
(b) 12
(c) 24
(d) 48
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D
(a) 4 3 1 2
(b) 4 1 3 2
(c) 2 1 3 4
(d) 2 3 1 4
Answer
B
Question. How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions ?
(a) 16
(b) 36
(c) 60
(d) 180
Answer
C
Question. 4 buses runs between Bhopal and Gwalior. If a man goes from Gwalior to Bhopal by a bus and comes back to Gwalior by another bus, then the total possible ways are
(a) 12
(b) 16
(c) 4
(d) 8
Answer
A
Question. If 10Cx= 10Cx+4, then the value of x is
(a) 5
(b) 4
(c) 3
(d) 2
Answer
C
Question. In a chess tournament where the participants were to play one game with one another, two players fell ill having played 6 games each, without playing among themselves. If the total number of games is 117, then the number of participants at the beginning was :
(a) 15
(b) 16
(c) 17
(d) 18
Answer
A
Question. A house master in a vegetarian boarding school takes 3 children from his house to the nearby dhaba for non-vegetarian food at a time as often as he can, but he does not take the same three children more than once. He finds that he goes to the dhaba (road side hotel) 84 times more than a particular child goes with him. Then the number of children taking non-vegetarian food in his hostel, is
(a) 15
(b) 5
(c) 20
(d) 10
Answer
D
Question. Number of 6 digit numbers that can be made with the digits 1, 2, 3 and 4 and having exactly two pairs of digits is
(a) 978
(b) 1801
(c) 1080
(d) 789
Answer
C
Question. What is the value of nP0?
(a) 0
(b) 1
(c) ∞
(d) 1/2
Answer
B
Question. If the letters of the word KRISNA are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word KRISNA is
(a) 324
(b) 341
(c) 359
(d) None of these
Answer
A
Question. If 10Cx= 10Cx+4 , then the value of x is
(a) 5
(b) 4
(c) 3
(d) 2
Answer
C
Question. In a circus, there are ten cages for accommodating ten animals. Out of these, four cages are so small that five out of 10 animals cannot enter into them. In how many ways will it be possible to accommodate ten animals in these ten cages?
(a) 66400
(b) 86400
(c) 96400
(d) None of these
Answer
B
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D E
(a) 4 5 2 3 1
(b) 1 3 5 2 4
(c) 4 2 5 3 1
(d) 1 5 3 2 4
Answer
A
Question. In how many ways can a bowler take four wickets in a single 6-ball over ?
(a) 6
(b) 15
(c) 20
(d) 30
Answer
B
Question. Five balls of different colours are to be placed in three boxes of different sizes. Each box can hold all five balls, Number or ways in which we can place the balls in the boxes (order is not considered in the box) so that no box remains empty is
(a) 150
(b) 160
(c) 12
(d) 19
Answer
A
Question. A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is
(a) 140
(b) 196
(c) 280
(d) 346
Answer
B
Question. Five balls of different colours are to be placed in three boxes of different sizes. Each box can hold all five balls. In how many ways can we place the balls so that no box remains empty?
(a) 50
(b) 100
(c) 150
(d) 200
Answer
C
Question. There are 10 true-false questions in a examination. Then these questions can be answered in:
(a) 100 ways
(b) 20 ways
(c) 512 ways
(d) 1024 ways
Answer
D
Question. Number of words each containing 3 consonants and 2 vowels that can be formed out of 5 consonants and 4 vowels is
(a) 3600
(b) 7200
(c) 6728
(d) 2703
Answer
B
Question. The number of values of r satisfying the equation 39C3r−1 − 39Cr2 = 39Cr−2 −39C3r
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. The number of chords that can be drawn through 21 points on a circle, is
(a) 200
(b) 190
(c) 210
(d) None of these
Answer
C
Question. There are 5 roads leading to a town from a village. The number of different ways in which a villager can go to the town and return back, is
(a) 25
(b) 20
(c) 10
(d) 5
Answer
A
Question. If eleven members of a committee sit at a round table so that the President and Secretary always sit together, then the number of arrangements is
(a) 10! × 2
(b) 10!
(c) 9! × 2
(d) 11! × 2!
Answer
C
Question. In an examination, there are three multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answers correct is :
(a) 11
(b) 12
(c) 27
(d) 63
Answer
D
STATEMENT TYPE QUESTIONS
Question. Consider the following statements.
I. The continued product of first n natural numbers is called the permutation.
II. L.C.M of 4!, 5! and 6! is 720.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
B
Question. Consider the following statements.
I. If some or all n objects are taken at a time, the number of combinations is 2n – 1.
II. An arrangement in a definite order which can be made by taking some or all of a number of things is called a permutation.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. The number of 3 letters words, with or without meaning which can be formed out of the letters of the word ‘NUMBER’.
Statement I : When repetition of letters is not allowed is 120.
Statement II : When repetition of letters is allowed is 216.
Choose the correct option.
(a) Only Statement I is correct
(b) Only Statement II is correct
(c) Both I and II are correct
(d) Both I and II are false
Answer
C
Question. Consider the following statements.
I. Three letters can be posted in five letter boxes in 35 ways.
II. In the permutations of n things, r taken together, the number of permutations in which m particular things occur together is n–mPr–m × rPm .
Choose the correct option.
(a) Only I is false.
(b) Only II is false.
(c) Both are false.
(d) Both are true.
Answer
C
Question. Consider the following statements.
If n is a natural number and r is non-negative integer such that 0 ≤ r ≤ n, then
I. nCr +nCr−1 = n+1Cr
II. nCr = n/r. n−1Cr−1
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. How many numbers can be made with the help of the digits 0, 1, 2, 3, 4, 5 which are greater than 3000: (repetition is not allowed)
(a) 180
(b) 360
(c) 1380
(d) 1500
Answer
C
Question. In the 13 cricket players 4 are bowlers, then how many ways can form a cricket team of 11 players in which at least 2 bowlers included:
(a) 55
(b) 72
(c) 78
(d) None of these
Answer
C
Question. In how many ways a team of 10 players out of 22 players can be made if 6 particular players are always to be included and 4 particular players are always excluded:
(a) 22C10
(b) 18C3
(c) 12C4
(d) 18C4
Answer
C
Question. The number of arrangement of the letters of the word “CALCUTTA”?
(a) 2520
(b) 5040
(c) 10080
(d) 40320
Answer
B
Question. There are 10 lamps in a hall. Each one of them can be switched on independently. The number of ways in which the hall can be illuminated is?
(a) 102
(b) 1023
(c) 210
(d) 10!
Answer
B
Question. Numbers greater than 1000 but not greater than 4000 which can be formed with the digits 0, 1, 2, 3, 4 (repetition of digits is allowed), are:
(a) 350
(b) 375
(c) 450
(d) 576
Answer
B
Question. If 2nC3 : nC2 = 44 :3; then for which of the following values of r , the value of nCr will be 15?
(a) r = 3
(b) r = 4
(c) r = 6
(d) r = 5
Answer
B
Question. If n2–nC2 = n2-n C10 , then n = ?
(a) 12
(b) 4 only
(c) −3 only
(d) 4 or −3
Answer
D
Question. How many words can be made from the letters of the word ‘COMMITTEE?’
(a) 9!/(2!)2
(b) 9!/(2!)3
(c) 9!/2!
(d) 9 !
Answer
B
Question. m men and n women are to be seated in a row, so that no two women sit together. If m > n , then the number of ways in which they can be seated is:
(a) m'(m+1)!/(m–n+1)!
(b) m'(m–1)!/(m–n+1)!
(c) (m–1)((m+1)!/(m–n+1)!
(d) None of these
Answer
A
Question. An n digit number is a positive number with exactly n digits. Nine hundred distinct n-digit numbers are to be formed using only the three digits 2, 5 and 7. The smallest value of n for which this is possible is:
(a) 6
(b) 7
(c) 8
(d) 9
Answer
B
Question. In how many ways can 15 members of a council sit along a circular table, when the Secretary is to sit on one side of the Chairman and the Deputy Secretary on the other side?
(a) 2×12!
(b) 24
(c) 2×15!
(d) None of these
Answer
A
Question. 20 persons are invited for a party. In how many different ways can they and the host be seated at a circular table, if the two particular persons are to be seated on either side of the host?
(a) 20!
(b) 2.18!
(c) 18!
(d) None of these
Answer
B
Question. The number of ways in which 5 beads of different colours form a necklace is:
(a) 12
(b) 24
(c) 120
(d) 60
Answer
A
Question. If 15C3r = 15Cr+3 then the value of r is:
(a) 3
(b) 4
(c) 5
(d) 8
Answer
A
Question. nCr /nCr-1 = ?
(a) n-r/r
(b) n+r-1/r
(c) n-r+1/r
(d) n-r-1/r
Answer
C
Question. A college offers 7 courses in the morning and 5 in the evening. The number of ways a student can select exactly one course, either in the morning or in the evening:
(a) 27
(b) 15
(c) 12
(d) 35
Answer
C
Question. In a monthly test, the teacher decides that there will be three questions, one from each of exercise 7, 8 and 9 of the text book. If there are 12 questions in exercise 7, 18 in exercise 8 and 9 in exercise 9, in how many ways can three questions be selected?
(a) 1944
(b) 1499
(c) 4991
(d) None of these
Answer
A
Question. In how many ways a team of 11 players can be formed out of 25 players, if 6 out of them are always to be included and 5 are always to be excluded:
(a) 2020
(b) 2002
(c) 2008
(d) 8002
Answer
B
Question. Out of 10 white, 9 black and 7 red balls, the number of ways in which selection of one or more balls can be made, is:
(a) 881
(b) 891
(c) 879
(d) 892
Answer
C
Question1. If n+1C3 = 2nC2 , then n =?
(a) 3
(b) 4
(c) 5
(d) 6
Answer
C
Question. In how many ways can 5 prizes be distributed among four students when every student can take one or more prizes?
(a) 1024
(b) 625
(c) 120
(d) 60
Answer
A
Question. The number of ways in which 9 persons can be divided into three equal groups is: D
(a) 1680
(b) 840
(c) 560
(d) 280
Question. A man has 7 friends. In how many ways he can invite one or more of them for a tea party:
(a) 128
(b) 256
(c) 127
(d) 130
Answer
C
Question. In how many ways can a girl and a boy be selected from a group of 15 boys and 8 girls?
(a) 15×8
(b) 15 + 8
(c) 23P2
(d) 23C2
Answer
A
Question. If eleven members of a committee sit at a round table so that the President and Secretary always sit together, then the number of arrangements is:
(a) 10!× 2
(b) 10!
(c) 9!× 2
(d) None of these
Answer
C
Question. In how many ways can 5 boys and 5 girls sit in a circle so that no two boys sit together?
(a) 5!×5!
(b) 4!× 5!
(c) 5 ! 5 !/2
(d) None of these
Answer
B
Question. In a conference of 8 persons, if each person shake hand with the other one only, then the total number of shake hands shall be:
(a) 64
(b) 56
(c) 49
(d) 28
Answer
D
Question. If the letters of the word ‘KRISNA’ are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word ‘KRISNA’ is:
(a) 324
(b) 341
(c) 359
(d) None of these
Answer
A
Question. How many triangles can be drawn by means of 9 noncollinear points?
(a) 84
(b) 72
(c) 144
(d) 126
Answer
A
Question. The number of straight lines joining 8 points on a circle is:
(a) 8
(b) 16
(c) 24
(d) 28
Answer
D
Question. We are to form different words with the letters of the word ‘INTEGER’. Let 1 m be the number of words in which I and N are never together, and 2 m be the number of words which begin with I and end with R. Then 1 2 m /m is equal to:
(a) 30
(b) 60
(c) 90
(d) 180
Answer
A
Question. If 8Cr = 8Cr+2 , then the value of rC2 is:
(a) 8
(b) 3
(c) 5
(d) 2
Answer
B
Question. Everybody in a room shakes hand with everybody else.
The total number of hand shakes is 66. The total number of persons in the room is:
(a) 11
(b) 12
(c) 13
(d) 14
Answer
B
Comprehension Based
Different words are being formed by arranging the letters of the word “SUCCESS”. All the words obtained by written in the form of a dictionary.
Question. The number of words in which the two C are together but no two S are together is:
a. 120
b. 96
c. 24
d. 420
Answer
C
Question. The number of words in which no two C and no two S are together is:
a. 120
b. 96
c. 24
d. 420
Answer
B
Question. The number of words in which the consonants appear in alphabetic order is:
a. 42
b. 40
c. 420
d. 280
Answer
A
Question. The rank of the word ‘SUCCESS’ in the dictionary is:
a. 328
b. 329
c. 330
d. 331
Answer
D
Question. The number of words in which the relative positions of vowels and consonants unaltered is:
a. 20
b. 60
c. 180
d. 540
Answer
A
Question. Consider all possible permutations of the letters of the word ENDEANOEL:

a. A→1; B→4; C→2; D→2
b. A→2; B→3; C→4; D→1
c. A→4; B→2; C→1; D→3
d. A→3; B→3; C→2; D→1
Answer
A
Question. Observe the following columns:

a. A→1,2,4; B→2,4; C→3,5
b.A→2,1,4; B→4,2, C→3,5
c. A→1,2,5; B→2,5; C→3,4
d.A→4,2,1; B→2,4; C→5,3
Answer
A
Question. If the number of ways of selecting n coupons out of an unlimited number of coupons bearing the letters A, T, C so that they cannot be used to spell to the used CAT is 189, then Σn2 must be:
Answer
91
Question. Let n1 < n2 < n3 < n4 < n5 be positive integers such that n1 + n2 + n3 + n4 + n5 = 20. The number of such distinct arrangements (n1 ,n2 ,n3 , n4 ,n5 ) is:
Answer
7
Question. If 12Pr = 11880, = then
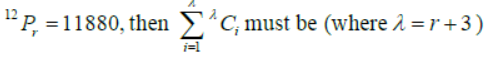
Answer
127
Question. The letters of the word PATNA are arrange in all possible ways as in a dictionary, then rank of the word PATNA from last is:
Answer
19
Question. The number of integral solutions of a + b + c = 0, a ≥ −5, b ≥ −5, c ≥ −5 must be:
Answer
136
Question. The sum of all values of r in
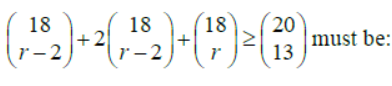
Answer
70
Question. Let n ≥ 2 be an integer. Taken n distinct points on a circle and join each pair of points by a line segment. Colour the line segment joining every pair of adjacent points by blue and the rest by red. If the number of red and blue line segments are equal, then the value of n is:
Answer
5