Please refer to Assignments Class 11 Mathematics Principle of Mathematical Induction Chapter 4 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 4 Principle of Mathematical Induction Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Principle of Mathematical Induction Assignments Class 11 Mathematics
Question. Let S(K) = 1+ 3+ 5…+ (2K -1) = 3+ K2 . Then which of the following is true
(a) Principle of mathematical induction can be used to prove the formula
(b) S(K) ⇒ S(K +1)
(c) S(K) ⤃ S(K +1)
(d) S(1) is correct
Answer
B
Question. Consider the statement: “P(n) : n2 – n + 41 is prime.” Then which one of the following is true?
(a) Both P(3) and P(5) are true.
(b) P(3) is false but P(5) is true.
(c) Both P(3) and P(5) are false.
(d) P(5) is false but P(3) is true.
Answer
A
Question. If
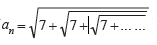
having n radical signs then by methods of mathematical induction which is true
(a) an > 7 ∀ n ≥ 1
(b) an < 7 ∀ n ≥ 1
(c) an < 4 ∀ n ≥ 1
(d) an < 3 ∀ n ≥ 1
Answer
B
Question. If the coefficients of x2 and x3 in the expansion of (3 + ax)9 are the same, then the value of a is:
(a) −7/9
(b) − 9/7
(c) 7/9
(d) 9/7
Number of Terms in the Expansion of (a + b + c)n and (a + b + c + d)n .
Answer
D
Question. If the number of terms in the expansion of (x − 2y + 3z)n is 45, then n = ?
(a) 7
(b) 8
(c) 9
(d) 5
Answer
B
Question. The middle term in the expansion of (1+x)2n x is:
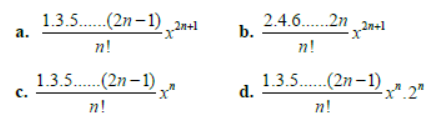
Answer
D
Question. The term independent of x in the expansion of (3x2/2− 1/3x)9 is:
(a) 7/12
(b) 7/18
(c) – 7/12
(d) – 7/16
Answer
B
Question. In the expansion of (1+ x)5 , the sum of the coefficient of the terms is:
(a) 80
(b) 16
(c) 32
(d) 64
Answer
C
Question. Find the coefficient of a3b4c5 in the expansion of (bc+ca+ab)6?
(a) 0
(b) 60
(c) –60
(d) 25
Answer
B
Question. If (1+ax)n = 1+8x+24x2 … then the value of aand n is:
(a) 2,4
(b) 2,3
(c) 1,2
(d) 1,2
Answer
A
Question. If the sum of coefficient in the expansion of (α2x2 − 2αx +1) vanishes, then the value of α is:
(a) 2
(b) –1
(c) 1
(d) –2
Answer
C
Question. If coefficient of (2r +3)th and (r − 1)th terms in the expansion of (1+ x)15 are equal, then value of r is:
(a) 5
(b) 6
(c) 4
(d) 3
Answer
A
Question. If the (r +1)th term in the expansion of
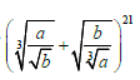
has the same power of a and b, then the value of r is:
(a) 9
(b) 10
(c) 8
(d) 6
Answer
A
Question. 10C1 + 10C3 + 10C5 + 10C7+ 10C9 = ?
(a) 29
(b) 210
(c) 210 −1
(d) None of these
Answer
A
Question. If (1+x)n = C0+C1x+C2x2 +….+Cnx2 ,then C02+C12x+C22 +C32+……+Cn2 =?
(a) n!/n!n!
(b) (2n)!/n!
(c) (2n)!/n!
(d) None of these
Answer
B
Question. If (1+x)n = C0+C1x+C2x2 +….+Cnx2 ,then
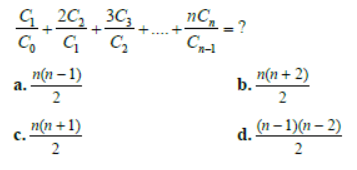
Answer
C
Question. If the coefficients of second, third and fourth term in the expansion of (1+x)2n are in (a)P., then 2n2−9n+7 is equal to:
(a) – 1
(b) 0
(c) 1
(d) 3/2
Answer
B
Question. The value of C1/2 + C3/4 + C5/6+……is equal to:
(a) 2n–1/n+1
(b) n.2n
(c) 2n/n
(d) 2n+1/n+1
Answer
A
Question. (1+x)n + x − nx −1 is divisible by: (where n∈ N )
(a) 2x
(b) 2 x
(c) 2x3
(d) All of these
Answer
B
Question. Sum of odd terms is A and sum of even terms is B in the expansion of (x + a)n , then:
(a) AB = 1/4(x–a)2n –(x+a)2n
(b) 2AB = 1/4(x+a)2n–(x–a)2n
(c) 4AB = 1/4(x+a)2n–(x–a)2n
(d) None of these
Answer
C
Question. The sum of all the coefficients in the binomial expansion of (x2 + x − 3)319 is:
(a) 1
(b) 2
(c) – 1
(d) 0
Answer
C
Question. The first 3 terms in the expansion of (1 + ax)n (n ≠ 0) are 1, 6x and 16x2. Then the value of a and n are respectively:
(a) 2 and 9 (b) 3 and 2
(c) 2/3 and 9
(d) 3/2 and 6
Answer
C
Question. Coefficient of x in the expansion of (x2+a/x) is:
(a) 9a2
(b) 10a3
(c) 10a2
(d) 10a
Answer
B
Question. C1 + 2C2 + 3C3 +….. nCn =?
(a) 2n
(b) n2n
(c) n2n-1
(d) n2n+1
Answer
C
Question. The coefficient of x5 in the expansion of (x2–x–2)5 is.
(a) – 83
(b) – 82
(c) – 81
(d) 0
Answer
C
Question. If a1, a2, a3, a4 are the coefficients of any four consecutive terms in the expansion of (1+ x)n ,then a1/a1+a2 + a3/a3+a4 = ?

Answer
C
Question. The largest term in the expansion of (3 + 2x)50 , where x=1/5 is:
(a) 5th
(b) 8th
(c) 7th
(d) 6th
Answer
C,D
Question. If
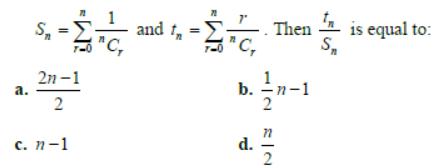
Answer
D
Question. 1/3√6–3x = ?
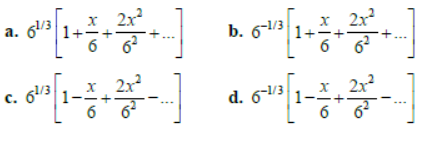
Answer
B
Question. (a/a+x)1/2 + (a/a–x)1/2
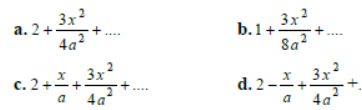
Answer
A
Question. The coefficient of xn in the expansion of (1 + x + x2 + …)−n is:
a. 1
b. ( − 1)n
c. n
d. n +1
Answer
B
Question. In the expansion of (2 – 2x + x2)9 ?
a. number of distinct terms is 10
b. coefficient of x4 is 97
c. sum of coefficient is 1
d. number of distinct terms is 55
Answer
B
Question. In the expansion of (3√4+14√6)20 ?
a. the number of rational terms = 4
b. the number of irrational terms =19
c. the middle term is irrational
d. the number of irrational terms = 17
Answer
C
Question. an = (1000)n/n! for n∈N. Then an is greatest, when:
a. n = 998
b. n = 999
c. n = 1000
d. n = 1001
Answer
C
Question. If the term independent of x in the expansion of (√x–λ/λ2)10 is 405, then value of λ is:
a. –3
b. 9
c. –9
d. 3
Answer
B
Question. (r +1)th term in the expansion of (1–x)–4 will be:
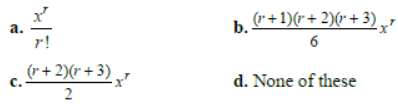
Answer
B
Question. 1 / (2 + x)4 = ?
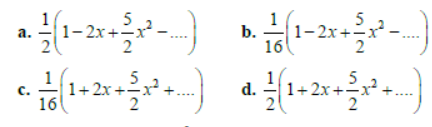
Answer
B
Question. If | x | > 1 , then (1 + x)−2 =?
a. 1 − 2x + 3x2 − ….
b. 1 + 2x + 3x2 + ….
c. 1 − 2/x + 3/x2 − ….
d. 1/x2 − 2/x3 + 3/x4 − ….
Answer
D
Question. In the expansion of(x + y +z) 25 =?
a. every term is of form 25Cr.rCk.X25-r .yr-k.2k
b. the coefficient of x8y9z9 is 0
c. the number of terms is 351
d. none of the above
Answer
D
Question. If (r + 1)th term is the first negative term in the expansion of (1+ x)7/2 , then the value of r is:
a. 5
b. 6
c. 4
d. 7
Answer
A
Assertion and Reason
Note: Read the Assertion (A) and Reason (R) carefully to mark the correct option out of the options given below:
a. If both assertion and reason are true and the reason is the correct explanation of the assertion.
b. If both assertion and reason are true but reason is not the correct explanation of the assertion.
c. If assertion is true but reason is false.
d. If the assertion and reason both are false.
e. If assertion is false but reason is true.
Question. Assertion: If n is an odd prime, then greatest integer contained in (2+√5)n –2n+1 is divisible by 20 n.
Reason: If p is a prime and 1≤r ≤p–1,then (P r) is divisible by p.
Answer
A
Question. Let (1+t)n = C0+C1t+C2t2…+Cntn
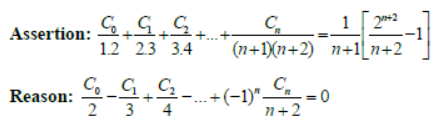
Answer
B
Question. Let
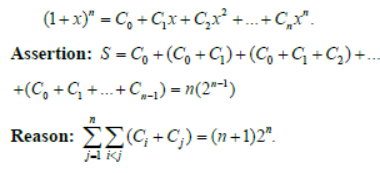
Answer
C
Question. Let (1+x)3n =
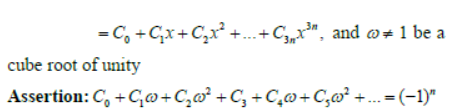
Reason: Cube roots unity form a triangle of area √3 square units.
Answer
C
Question.
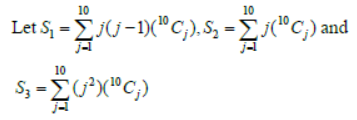
Assertion: S3 = 55 × 29
Reason: S1 = 90 × 28
and S2 = 10 × 28
Answer
C
Question. sin(rx)cos{(n-r)} = f(n)sin(nx) then the value of f(13) must be:
Answer
4096
Question.
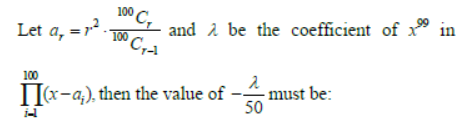
Answer
3333
Question. The coefficients of three consecutive terms of (1+x)n+5 are in the ratio 5 : 10 : 14. Then, n is equal to:
Answer
6
Paragraph
where a1, a2, a3……, a4n are real number and n is a positive integer.
Question. The value of
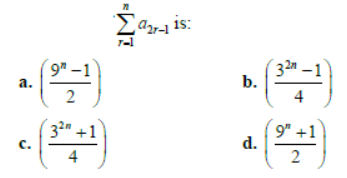
Answer
B
Question. The value of a2 is:
a. 4n+1C2
b. 3n+1C2
c. 2n+1C2
d. n+1C2
Answer
C
Question. The value of a4n–1 is:
a. 2n
b. 2n2 + 4n
c. 2n + 3
d. 2n2 + 3n
Answer
A
Question. The correct statement is:
a. ar = an–r, 0 ≤ r ≤ n
b. ar – r = an–r, 0 ≤ r ≤ n
c. ar = a2n, 0 ≤ r ≤ 2n
d. ar = a4n–r, 0 ≤ r ≤ 4n
Answer
D
Question. The value of
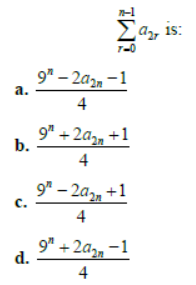
Answer
C


