Assignments Class 11 Mathematics Complex Numbers and Quadratic Equations

Please refer to Assignments Class 11 Mathematics Complex Numbers and Quadratic Equations Chapter 5 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 5 Complex Numbers and Quadratic Equations Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.

Complex Numbers and Quadratic Equations Assignments Class 11 Mathematics

Question. If z = a + ib, then real and imaginary part of z are
(a) Re(z) = a, Im(z) = b
(b) Re(z) = b, Im(z) = a
(c) Re(z) = a, Im(z) = ib
(d) None of these 

Question. The conjugate of the complex number 2+5i/4–3i is equal to :
(a) 7– 26i/25
(b) –7– 26i/25
(c) – 7+26i/25
(d) 7+26i/25

Question. The solution of √3x² – 2 = 2x –1 are :
(a) (2, 4)
(b) (1, 4)
(c) (3, 4)
(d) (1, 3) 

Question. If z = x –i y and z³ = p + iq, then (x/p + y/q) / (p² + q²) is equal to
(a) –2
(b) –1
(c) 2
(d) 1 

Question. Simplify the complex numbers given in column-I and match with column-II. 

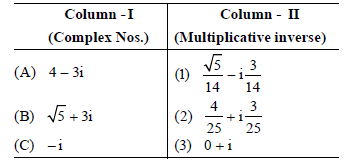
Codes:
     A B C
(a) 1 2 3
(b) 2 1 3
(c) 1 3 2
(d) 2 3 1 

Question. If one root of ax² + bx + c = 0 be square of the other, then the value of b³ + ac² + a² c is
(a) 3abc
(b) –3abc
(c) 0
(d) None of these

Question. The value of 

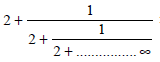
(a) 1 – √2
(b) 1 + √2
(c) 1 ± √2
(d) None of these 

Question. If z is a complex number such that z – 1/z + 1 is purely imaginary, then
(a) |z | = 0
(b) |z | = 1
(c) |z | > 1
(d) |z | < 1 

Question. Find the value of a such that the sum of the squares of the roots of the equation x² – (a – 2)x – (a + 1) = 0 is least.
(a) 4
(b) 2
(c) 1
(d) 3

Question. If z₁ = 2 + 3i and z₂ = 3 – 2i, then z₁ – z₂ equals to –1 + bi. The value of ‘b’ is
(a) 1
(b) 2
(c) 3
(d) 5 

Question. If z is a complex number such that z₂ = (z̄)² , then
(a) z is purely real
(b) z is purely imaginary
(c) either z is purely real or purely imaginary
(d) None of these 

Question. Simplify the complex numbers given in column-I and match with column-II 

Codes:
     A B C D
(a) 1 2 3 4
(b) 2 1 3 4
(c) 2 3 4 1
(d) 1 4 3 2 

Question. The roots of the given equation (p – q) x² + (q – r) x + (r – p) = 0 are :
(a) p–q/r–p,1
(b) q–r/p–q,1
(c) r–p/p–q,1
(d) None of these 

Question. If x = √–16, then
(a) x = 4i
(b) x = 4
(c) x = – 4
(d) All of these 

Question. If (x + iy)^1/3 = a + ib, where x, y, a, b ∈ R, then x/a – y/b =
(a) a² – b²
(b) –2(a² + b²)
(c) 2(a² – b²)
(d) a² + b² 

Question. Product of real roots of the equation t²x²+|x|+9 = 0
(a) is always positive
(b) is always negative
(c) does not exist
(d) None of these 

Question. The value of (1 + i)⁴ (1 + 1/1)⁴ is
(a) 12
(b) 2
(c) 8
(d) 16 

Question. If α, β be the roots of the equation 2x² – 35x + 2 = 0, then the value of (2α – 35)3 . (2β – 35)3 is equal to
(a) 1
(b) 64
(c) 8
(d) None of these 

Question. The roots of equation x–2/x–1 = 1– 2/x–1 is
(a) one
(b) two
(c) infinite
(d) None of these

Question. The solutions of the quadratic equation ax² + bx + c = 0, where a, b, c ∈ R, a ≠ 0, b² – 4ac < 0, are given by x = ? 

Question. Solve √5x² + x + √5 = 0.
(a) ± √19/5 i
(b) ± √19i/2
(c) – 1± √19i/2√5
(d)  – 1± √19i/√5

Question. If the roots of the equation x² – 5x + 16 = 0 are α, β and the roots of equation x² + px + q = 0 are α² + β², αβ/2 ,then
(a) p = 1, q = –56
(b) p = –1, q = –56
(c) p = 1, q = 56
(d) p = –1, q = 56 

Question. Evaluate: (1 + i)⁶ + (1 – i)³.
(a) –2 – 10i
(b) 2 – 10i
(c) –2 + 10i
(d) 2 + 10i 

Question. If z₁ = √3 + i√3 and z₂ = √3 + i , then in which quadrant z₁/z₂ lies?
(a) I
(b) II
(c) III
(d) IV 

Question. Value of (2i/1+i)² is
(a) i
(b) 2i
(c) 1 – i
(d) 1 – 2i 

Question. If z(2 – i) = (3 + i), then z²⁰ is equal to
(a) 2¹⁰
(b) –2¹⁰
(c) 2²⁰
(d) –2²⁰ 

Question. If z₁ = 3 + i and z₂ = i – 1, then
(a) | z₁ + z₂| > |z₁| + |z₂|
(b) | z₁+ z₂ | < |z₁| – |z₂|
(c) |z₁ + z₂| ≤ |z₁| + |z₂|
(d) |z₁ + z₂| < |z₁| + |z₂|

Question. Simplify the complex numbers given in column-I and match with column-II

Codes:
     A B C D E
(a) 5 4 3 2 1
(b) 4 1 5 2 3
(c) 4 2 5 1 3
(d) 3 1 2 5 4 

Question. Let z be any complex number such that | z | = 4 and arg (z) = 5π/6 , then value of z is
(a) –2√3 – 2i
(b) 2√3 – i
(c) √2 + 3i
(d) –2√3 + 2i 

Question. If α, β are the roots of the equation ax² + bx + c = 0, then the value of 1/aα + b + 1/aβ + b equals
(a) ac/b
(b) 1
(c) ab/c
(d) b/ac 

Question. If x² + y² = 25, xy = 12, then x =
(a) {3, 4}
(b) {3, –3}
(c) {3, 4, –3, –4}
(d) {–3, –3} 

Question. If x² + ax + 10 = 0 and x² + bx – 10 = 0 have a common root, then a² – b² is equal to
(a) 10
(b) 20
(c) 30
(d) 40 

Question. i⁵⁷ + 1 /i²⁵  when simplified has the value
(a) 0
(b) 2i
(c) – 2i
(d) 2 

Question. The modulus of (1 + i√3)(2 +2i)/(√3–i) is
(a) 2
(b) 4
(c) 3√2
(d) 2√2

Question. If the product of the roots of the equation (a + 1)x² + (2a + 3)x + (3a + 4) = 0 be 2, then the sum of roots is
(a) 1
(b) –1
(c) 2
(d) –2 

Question. Modulus of z = (1 + i√3)(cosθ+ isinθ)/2(1 – i)(cosθ– isinθ)  is
(a) 1/√3
(b) – 1/√2
(c) 1/√2
(d) 1 

Question. The argument of the complex number (i/2 – 2/i) is equal to
(a) π/4
(b) 3π/4
(c) π/12
(d) π/2 

Question. Value of k such that equations 2x² + kx – 5 = 0 and x² – 3x – 4 = 0 have one common root, is
(a) –1, –2
(b) –3, –27/4
(c) 3, 4/27
(d) –2, – 3

Question. √–3 √–6 is equal to
(a) 3√2
(b) –3√2
(c) 3√2 i
(d) –3√2i 

Question. If the complex numbers z₁, z₂,z₃ represents the vertices of an equilateral triangle such that | z₁ | = | z₂ | = | z₃ |, then value of z₁ + z₂ + z₃ is
(a) 0
(b) 1
(c) 2
(d) 3/2 

Question. If α and β are the roots of the equation x² + 2x + 4 = 0, then 1/α³ + 1/β³ is equal to
(a) – 1/2
(b) 1/2
(c) 32
(d) 1/4 

Question. Amplitude of 1+√3i/√3+1 is :
(a) π/6
(b) π/4
(c) π/3
(d) π/2 

Question. If the sum of the roots of the equation x² + px + q = 0 is three times their difference, then which one of the following is true?
(a) 9p² = 2q
(b) 2q² = 9p
(c) 2p² = 9q
(d) 9q² = 2p 

Question. If a < b < c < d, then the nature of roots of ( x – a) (x – c) + 2 (x – b) (x – d) = 0 is
(a) real and equal
(b) complex
(c) real and unequal
(d) None of these

Question. Which of the following is correct for any two complex numbers z₁ and z₂?
(a) |z₁ z₂| = |z₁| |z₂|
(b) arg(z₁ z₂) = arg(z₁) . arg(z₂)
(c) |z₁ + z₂| = |z₁| + |z₂|
(d) |z₁ + z₂| ≥ |z₁| – |z₂| 

Question. The value of (1 + i)⁵ (1 – i)⁵ is 2ⁿ. ‘n’ is equal to
(a) 2
(b) 3
(c) 4
(d) 5 

Question. The complex number 1+ 2i/1–i lies in:
(a) I quadrant
(b) II quadrant
(c) III quadrant
(d) IV quadrant 

Question. For the equation 1/x + a – 1/x + b = 1/x + c , if the product of roots is zero, then sum of roots is
(a)– 2bc/b+c
(b) 2ca/c + a
(c) bc/c + a
(d) –bc/b+c 

Question. Represent z = 1 + i √3 in the polar form.
(a) cosπ/3 + i sinπ/3
(b) cosπ/3 – i sinπ/3
(c) 2 (cosπ/3 + i sinπ/3)
(d) 4 cosπ/3 + i sinπ/3) 

Question. If z₁ = 2 – i and z₂ = 1 + i, then value of |z₁ + z₂ + 1/z₁ – z₂ + 1| is
(a) 2
(b) 2i
(c) 2
(d) 2i 

Question. If z₁ = 2 + 3i and z₂ = 3 + 2i, then z₁ + z₂ equals to a + ai. Value of ‘a’ is equal to
(a) 3
(b) 4
(c) 5
(d) 2 

Question. If the sum of the roots of the equation x² + px + q = 0 is equal to the sum of their squares, then
(a) p² – q² = 0
(b) p² + q² = 2q
(c) p² + p = 2q
(d) None of these 

Question. The value of (1 + i)⁸ + (1 – i)⁸ is 2n. Value of n is
(a) 2
(b) 3
(c) 4
(d) 5 

Question. If ax² + bx + c = 0 is a quadratic equation, then equation has no real roots, if
(a) D > 0
(b) D = 0
(c) D < 0
(d) None of these 

Question. If z be the conjugate of the complex number z, then which of the following relations is false?
(a) |z| =| z̄|
(b) z.z̄ = | z̄|²
(c)  z̄₁ + z̄₂ = z̄₁ + z̄₂
(d) arg z = arg z̄ 

Question. Additive inverse of 1 – i is
(a) 0 + 0i
(b) –1 – i
(c) –1 + i
(d) None of these

Question. The roots of the equation 3^2x – 10.3^x + 9 = 0 are
(a) 1, 2
(b) 0, 2
(c) 0, 1
(d) 1, 3 

Question. If 2 + i√3 is a root of the equation x² + px + q = 0, where p and q are real, then (p, q) =
(a) (–4, 7)
(b) (4, –7)
(c) (4, 7)
(d) (–4, –7) 

Question. If x² + x + 1 = 0, then what is the value of x ?
(a) 1 + √3i/2
(b) –1 ± √3i/2
(c) –1 ± √3i/3
(d) –1 ± √2i/2 

Question. (1/1–2i + 3/1+i)(3+4i/2–4i)is equal to :
(a) 1/2 + 9/2i
(b) 1/2 – 9/2i
(c) 1/4 – 9/4i
(d) 1/4 + 9/4i