Please refer to Introduction to Three Dimensional Geometry Class 11 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 11 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 11 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 11.
Class 11 Mathematics Important Questions Introduction to Three Dimensional Geometry
Assertion & Reasoning Based MCQs :
(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.
Question. Assertion : The foot of perpendicular drawn from the point A(1, 2, 8) on the xy-plane is (1, 2, 0).
Reason : Equation of xy-plane is y = 0.
Answer
C
Question. Assertion : The distance between the points (1 + 11, 0, 0) and (1, –2, 3) is 2 6 units.
Reason : Distance between any two points A(x1, y1, z1) and B(x2, y2, z2) is, |AB|=√(x2+x1)2 + (y2+y1)2 + (z2+z1)2
Answer
C
Question. Assertion : The points A(3, –1, 2), B(1, 2, – 4), C(–1, 1, 2) and D(1, –2, 8) are the vertices of a parallelogram.
Reason : Coordinates of mid-point of a line joining the points A(x1, y1, z1) and B(x2, y2, z2) is (x1+x2/2 , y1+y2/2 , z1+z2/2) .
Answer
A
Question. Assertion : The points A(1, –1, 3), B(2, –4, 5) and C(5, –13, 11) are collinear.
Reason : If AB + BC = AC, then A, B, C are collinear.
Answer
A
Question. Assertion : Coordinates of centroid of a triangle formed by the vertices A(3, 2, 0), B(5, 3, 2) and C(0, 2, 4) is (8/3 , 8/3 , 8/3) .
Reason : Coordinates of centroid of a triangle with vertices A(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3) is (x1 + x2 + x3/3 , y1 + y2 + y3/3 , z1 + z2 + z3/3) .
Answer
D
Very Short Answer Type Questions :
Question. If a point lies on the y-axis, then what are its x-coordinate and z-coordinate?
Answer: If a point lies on y-axis, then its x-coordinate is 0 and z-coordinate is 0.
Question. Find the distance of (1, 2, 5) from x-axis.
Answer: Let L be the foot of perpendicular drawn from
A(1, 2, 5) to the x-axis.
Then, coordinates of L ≡ (1, 0, 0).
∴ Required distance AL
= √(1 − 1)2 + (2 − 0)2 + (5 − 0)2 = √4 + 25
= √29 units.
Question. Find the distance of the point P(4, –3, 5) from XY plane.
Answer: The coordinates of foot of perpendicular L from
P(4, –3, 5) on XY-plane is given by L(4, –3, 0)
∴ Required distance
= √(4 − 4)2 + (−3 + 3)2 + (0 − 5)2 = √25 = 5 units.
Question. Write the distance of the point A(3, 4, 5) from z-axis.
Answer: The coordinates of foot of perpendicular
R from A(3, 4, 5) on z-axis is given by R(0, 0, 5)
∴ Required distance = √(0 − 3)2 + (0 − 4)2 + (5 − 5)2
= √9 + 16 + 0 = 25 = 5 units.
Question. If a point lies in yz-plane, then what is its x-coordinate?
2. If a point lies in yz-plane, then its x-coordinate is 0.
Question. What is the distance of the point (3, 4, 5) from the YZ plane?
Answer: The coordinates of foot of perpendicular from the
point (3, 4, 5) on YZ plane are (0, 4, 5).
∴ Required distance = √(0 − 3)2 + (4 − 4)2 + (5 − 5)2
= √9 + 0 + 0 = 3 units .
Question. A point is on the x-axis. Write its y-coordinate and z-coordinate.
Answer: A point on the x-axis is of the form(x, 0, 0).
∴ y-coordinate = 0 and z-coordinate = 0.
Question. Determine the octant of (4, –3, –1).
Answer: Since, x coordinate is positive while y and z, coordinates are negative.
∴ (4, –3, –1) lies in VIII octant.
Question. In which octant does (–1, –6, 5) lies?
Answer: Since, x and y coordinates are negative while z coordinate is positive.
∴ (–1, –6, 5) lies in III octant.
Question. Find the distance of (1, –2, 7) from the y-axis.
Answer: The coordinates of foot of perpendicular from (1, –2, 7)
on y-axis are (0, –2, 0)
∴ Required distance =
√(0 − 1)2 + (−2 + 2)2 + (0 − 7)2
= √1 + 0 + 49 = 50 = 5√2 units.
Short Answer Type Questions :
Question. Find the coordinates of the point which divides the join of P(2, –1, 4) and Q(4, 3, 2) in the ratio 2 : 3 internally.
Answer: Let R(x, y, z) be the required point.
If R divides PQ internally in the ratio 2 : 3, then
x = 2 x 4 + 3 x 2/2+3 , y = 2 x 3 + 3(-1)/2+3
and z = 2x2 + 3x4/2+3
[∴ (x,y,z) = (mx2 + nx1/m+n , my2 + ny1/m+n , mz2 + nz1/m+n)]
⇒ x = 14/5 , y = 3/5 and z = 16/5
So, the coordinates of point R are (14/5 , 3/5 , 16/5) .
Question. A point R with x-coordinate 4 lies on the line segment joining the points P(2, –6, 4) and Q(8, 6, 10).
Find the coordinates of the point R.
Answer: Suppose R(4, y, z) be any point which divides PQ in the ratio l : 1 internally.

Then, the coordinates of R are
(8λ+2/λ+1 , 6λ – 6/λ+1 , 10λ + 4/λ+1)
Since x-coordinate of R is 4.
∴ 8λ+2/λ+1 = 4 ⇒ 8λ + 2 = 4λ + 4 ⇒ 4λ = 2 ⇒ λ = 1/2 .
∴ y = 6(1/2)-6/1/2+1 = − 2 and z = 10(1/2)+4/1/2+1
Hence, the coordinates of R are (4, –2, 6).
Question. Using section formula, show that the points A(2, –3, 4), B(–1, 2, 1) and C(0,1/3,2) are collinear.
Answer: Suppose the given points are collinear
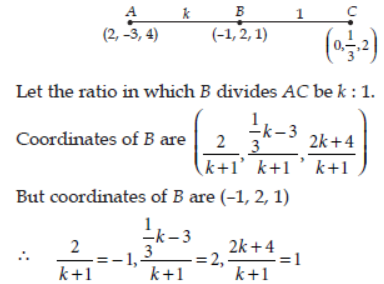
From each of these equations, we get k = – 3
Since each of these equations give the same value of k.
∴ The given points are collinear.
Question. Let P and Q be any two points. Find the coordinates of the point R which divides PQ externally in the ratio 2 : 1 and verify that Q is the mid-point of PR.
Answer: Let the coordinates of points P and Q be (x1,y1, z1) and (x2, y2, z2) respectively.
Then, the coordinates of the point R which divides PQ externally in the ratio 2 : 1 are
(2x2 – x1/2-1 , 2y2 -y1/2-1 , 2z2-z1/2-1)
=(2x2 – x1, 2y2 – y1, 2z2 – z1)
The coordinates of the mid-point of PR are
(x1+2x2-x1/2 , y1+2y2-y1/2 , z1+2z2-z1/2) = (x2, y2, z2)
Clearly, these are the coordinates of point Q. Hence, Q is the mid-point of PR.
Question. Find the locus of the point which is equidistant from the points A(0, 2, 3) and B(2, –2, 1).
Answer: Let P(x, y, z) be any point which is equidistant from
A(0, 2, 3) and B(2, –2, 1).
Then, PA = PB ⇒ PA2 = PB2
⇒ (x −0)2 +(y −2)2 +(z−3)2 = (x − 2)2 + (y + 2)2 + (z − 1)2
⇒ 4x – 8y – 4z + 4 = 0 ⇒ x – 2y – z + 1 = 0
Hence, the required locus is x – 2y – z + 1 = 0
Question. Verify that (3, –2, 4), (1, 0, –2), (–1, 2, –8) are collinear.
Answer: Let A(3, –2, 4), B(1, 0, –2) and C(–1, 2, –8) be given points.
∴ By distance formula,
AB = √(1 − 3)2 + (0 + 2)2 + (−2 − 4)2
= √4 + 4 + 36 = 44 = 2 √11 units
BC = √(−1 − 1)2 + (2 − 0)2 + (−8 + 2)2
= √4 + 4 + 36 = 44 = 2 √11 units
AC = √(−1 − 3)2 + (2 + 2)2 + (−8 − 4)2
= √16 + 16 + 144 = 176 = 4 √11 units
∴ AB + BC = 4 √11 units = AC
Thus, the given points are collinear.
Question. Show that the points A(0, 7, 10), B(–1, 6, 6) and C(–4, 9, 6) form an isosceles right-angled triangle.
Answer: Given, A(0, 7, 10), B(–1, 6, 6) and C(–4, 9, 6)
∴ Using distance formula, we get,
AB= √(−1 − 0)2 +(6 − 7)2 +(6 − 10)2 = √18 =3 √2
BC = √(−4 + 1)2 + (9 − 6)2 + (6 − 6)2 = √18 = 3 √2
AC = √(−4 − 0)2 + (9 − 7)2 + (6 − 10)2 = √36 = 6
Clearly, AB = BC and AB2 + BC2 = 18 + 18 = 36 = AC2.
Hence, triangle ABC is an isosceles right-angled triangle.
Question. Let A(2, 2, –3), B(5, 6, 9), C(2, 7, 9) be the vertices of a triangle. The internal bisector of the angle A meets BC at the point D. Find the coordinates of D.
Answer: Let the coordinates of D be (x, y, z)

AB = √9 + 16 + 144 = √169 = 13 units
AC = √0 + 25 + 144 = √169 = 13 units
Now, BD/DC = AB/AC = 13/13 = 1/1
⇒ BD = DC
Since, D divides the line BC in two equal parts. So, D is the mid-point of BC.
∴ By using the mid-point formula,
x = 5+2/2 = 7/2
y = 6+7/2 = 13/2 and z = 9+9/2 = 9
Hence, the coordinates of D are (7/2 , 13/2 ,9) .
Question. Find the point in yz-plane which is equidistant from the points A(3, 2, –1), B(1, –1, 0) and C(2, 1, 2).
Answer: Let P be a point in the yz plane. The point in the yz
plane is of the form P(0, y, z).
∴ P is equidistant from A(3, 2, –1), B(1, –1, 0) and C(2, 1, 2)
∴ AP = BP = CP ⇔ AP2 = BP2 and BP2 = CP2
⇒ (0 – 3)2 + (y – 2)2 + (z + 1)2 = (0 – 1)2 + (y + 1)2 + (z – 0)2
and (0 – 1)2 + (y + 1)2 + (z – 0)2 = (0 – 2)2 + (y – 1)2 + (z – 2)2
⇒ 3y – z – 6 = 0 …(i) and 4y +4z – 7 = 0 …(ii)
On solving (i) and (ii), we get y = 31/16 and z = -3/16
Hence, the required point is (0,31/16,-3/16) .
Question. Prove that the coordinates of the centroid of the triangle whose vertices are (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) are (x1 + x2 + x3/3 , y1 + y2 + y3/3 , z1 + z2 + z3/3) .
Answer: Let G be the centroid of a triangle ABC. We know, centroid of a triangle divides each median in the ratio 2 : 1.
As, D is mid-point of BC.
∴ Coordinates of D are

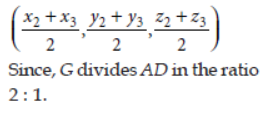
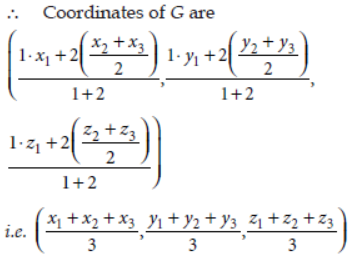
Question. Three vertices of a parallelogram PQRS are P(3, –1, 2), Q(1, 2, –4) and R(–1, 1, 2). Find the coordinates of the fourth vertex.
Answer: Let the required vertex be S(x, y, z)

Question. Show that the three points A(2, 3, 4), B(–1, 2, –3) and C(–4, 1, –10) are collinear and find the ratio in which C divides AB.
Answer: We have given, A(2, 3, 4), B(–1, 2, –3) and C(–4, 1, –10).
Now, AB = √(2 + 1)2 + (3 − 2)2 + (4 + 3)2
= √9 + 1+ 49 = √59 units
BC = √(−1+ 4)2 + (2 − 1)2 + (−3 + 10)2
= √9 + 1+ 49 = √59 units
AC =√(2 + 4)2 + (3 − 1)2 + (4 + 10)2
= √36 + 4 + 196 = √236 = 2 √59 units
Now, AC = AB + BC
So, the points A, B and C are collinear.
Also, AC : BC = 2 59 : 59 = 2 : 1
Hence, C divides AB in the ratio 2:1 externally.
Question. Find the coordinates of a point on the y-axis which are at a distance of 5 2from the point P(3, –2, 5).
Answer: Let Q(0, y, 0) be any point on y-axis.
Then, PQ = √(0 − 3)2 + (y + 2)2 + (0 − 5)2
= √9 + y2 + 4 + 4y + 25 = √y2 + 4y + 38
Given, PQ = 5 √2Let the coordinates of D be (x, y, z)
⇒ √y2 + 4y + 38 = 5 √2.
On squaring both sides, we get
y2 + 4y + 38 = 50 ⇒ y2 + 4y – 12 = 0
⇒ (y – 2)(y + 6) = 0 ⇒ y = 2, –6
Thus, coordinates of point Q are (0, 2, 0) and (0, –6, 0).
Question. Find the coordinates of the points which trisect the line segment joining the points P(4, 2, –6) and Q(10, –16, 6).
Answer: (b) : Let R and S be two points which trisect the join of PQ.

Question. Determine the values of a and b so that the points (a, b, 3), (2, 0, –1) and (1, –1, –3) are collinear.
Answer: Suppose the given points are P(a, b, 3), Q(2, 0, –1) and R(1, –1, –3)

Question. Find the coordinates of the point which divides the join of P(2, –1, 4) and Q(4, 3, 2) in the ratio 2 : 3 externally.
Answer: Let R(x, y, z) be any point which divides PQ externally in the ratio 2 : 3, then

Question. Find the ratio in which YZ-plane divides the line segment joining points (–2, 4, 7) and (3, –5, 8). Also, find the coordinates of the point of intersection.
Answer: Let point R(x, y, z) divides the join of (–2, 4, 7) and (3, –5, 8) in the ratio k : 1, then point of division is


Question. If the origin is the centroid of the triangle PQR with vertices P(2a, 2, 6), Q(–4, 3b, –10) and R(8, 14, 2c), then find the values of a, b and c.
Answer: Vertices of ΔPQR are P(2a, 2, 6),
Q(–4, 3b, –10) and R(8, 14, 2c).
Centroid of ΔPQR is :

Question. Find the points of trisection of the segment joining the points A(1, 0, –6) and B(–5, 9, 6).
Answer: Let P and Q be the points of trisection of the segment [AB], then P divides [AB] in the ratio 1 : 2 and Q divides [AB] in the ratio 2 : 1.
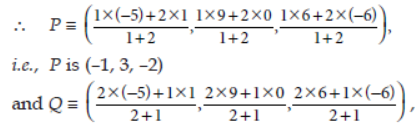
i.e., Q is (–3, 6, 2).
Hence, the required points of trisection are P(–1, 3, –2) and Q(–3, 6, 2).
Question. Prove that the points (0, –1, –7), (2, 1, –9) and (6, 5, –13) are collinear. Find the ratio in which the first point divides the join of the other two.
Answer: Let the given points be A(0, –1, –7), B(2, 1, –9) and C(6, 5, –13)
Now, AB = √(0 − 2)2 + (−1− 1)2 + (−7 + 9)2
= √4 + 4 + 4 = 2 √3 units
BC = √(2 − 6)2 + (1− 5)2 + (−9 + 13)2
= √16 + 16 + 16 = 4 √3 units
AC = √(0 − 6)2 + (−1− 5)2 + (−7 + 13)2
= √36 + 36 + 36 = 6 √3 units
Now, AC = AB + BC
∴ The points A, B and C are collinear.
Now, AB : AC = 2 √3 : 6 √3 = 1: 3
Hence, point A divides B and C in the ratio 1 : 3 externally.
Question. Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
Answer: Let A(x, y, z) be any point which is equidistant from
points B(1, 2, 3) and C(3, 2, –1).
Then AB = √(x − 1)2 + (y − 2)2 + (z − 3)2
AC = √(x − 3)2 + (y − 2)2 + (z + 1)2
It is given that AB = AC
√(x − 1)2 + (y − 2)2 + (z − 3)2
= √(x − 3)2 + (y − 2)2 + (z + 1)2
⇒ √(x – 1)2 + (y – 2)2 + (z – 3)2
= √(x – 3)2 + (y – 2)2 + (z + 1)2
⇒ x2 + 1 – 2x + z2 + 9 – 6z = x2 + 9 – 6x + z2 + 1 + 2z
⇒ –2x – 6z + 10 = –6x + 2z + 10
⇒ –2x – 6z + 6x – 2z = 0
⇒ 4x – 8z = 0 ⇒ x – 2z = 0
Question. Find the third vertex of triangle whose centroid is origin and two vertices are (2, 4, 6) and (0, –2, –5).
Answer: Let third vertex of DABC be A(α, β, γ)

Since the coordinates of centroid G are (0, 0, 0)
⇒ 0 = α + 2 + 0/2 ⇒ α = -2
⇒ 0 = β + 4 – 2/3 ⇒ β = -2
⇒ 0 = γ + 6 – 5/3 ⇒ γ = -2
So, the third vertex of the triangle is A(–2, –2, –1).
Question. Find the point on y-axis which is equidistant from the point A(3, 2, 2) and B(5, 5, 4).
Answer: The point on the y-axis is of the form P(0, y, 0). Since the points A(3, 2, 2) and B (5, 5, 4) are equidistant from P.
∴ PA = PB ⇒ PA2 = PB2
⇒ (0 – 3)2 + (y – 2)2 + (0 – 2)2 = (0 – 5)2 + (y – 5)2 + (0 – 4)2
⇒ 6x = 25 + 25 + 16 – 17 i.e., y = 49/6
Thus, the point P(0,49/6,0) , on the y-axis is equidistant from A and B.
Question. Show that the triangle ABC with vertices A(0, 4, 1), B(2, 3, –1) and C(4, 5, 0) is right angled.
Answer: We have given A(0, 4, 1), B(2, 3, –1) and C(4, 5, 0).
By using distance formula, we get
AB = √(0 − 2)2 + (4 − 3)2 + (1 + 1)2
= √4 + 1 + 4 = √9 = 3 units
BC = √(2 − 4)2 + (3 − 5)2 + (−1 − 0)2
= √4 + 4 + 1 = √9 = 3 units
AC = √(0 − 4)2 + (4 − 5)2 + (1 − 0)2
= √16 + 1 + 1 = √18 units
Now, AB2 + BC2 = 9 + 9 = 18 = AC2.
Hence, DABC is a right angled triangle.
Question. Find the lengths of the medians of the triangle with vertices A(0, 0, 8), B(0, 6, 0) and C(6, 0, 0).
Answer: Let D, E and F be the mid-points of sides BC, CA and AB respectively.

∴ AD = √(0 − 3)2 + (0 − 3)2 + (8 − 0)2
= √9 + 9 + 64 = √82 units
BE = √(0 − 3)2 + (6 − 0)2 + (0 − 4)2
= √9 + 36 + 16 = √61 units
and, CF = (6 − 0)2 + (0 − 3)2 + (0 − 4)2
= 36 + 9 + 16 = √61 units
Long Answer Type Questions :
Question. Find the equation of the set of points P, the sum of whose distances from A(4, 0, 0) and B(–4, 0, 0) is equal to 10.
Answer: Let P(x, y, z) be any point.
Then, PA = √(x − 4)2 + (y − 0)2 + (z − 0)2
= √x2 + 16 – 8x + y2 + z2
and PB = √(x + 4)2 + (y − 0)2 + (z − 0)2
= √x2 + 16 – 8x + y2 + z2
It is given that PA + PB = 10
∴ √x2 + 16 − 8x + y2 + z2 + √x2 + 16 + 8x + y2 + z2 = 10
⇒ √x2 + 16 − 8x + y2 + z2
= 10 − x2 + 16 + 8x + y2 + z2 …(i)
Squaring (i) on both sides, we get
x2 + 16 – 8x + y2 + z2 = 100 + x2 + 16 + 8x + y2 + z2
−√20 x2 + 16 + 8x + y2 + z2
⇒ 20 √x2 + 16 + 8x + y2 + z2 = 16x + 100
⇒ 5 √x2 + 16 + 8x + y2 + z2 = 4x + 25 …(ii)
Squaring (ii) on both sides, we get
25(x2 + 16 + 8x + y2 + z2) = 16x2 + 625 + 200x
⇒ 25x2 + 400 + 200x + 25y2 + 25z2 – 16x2
– 625 – 200x = 0
⇒ 9x2 + 25y2 + 25z2 – 225 = 0
∴ Required equation is 9x2 + 25y2 + 25z2 – 225 = 0
Question. The mid-points of the sides of a triangle are (1, 5, –1), (0, 4, –2) and (2, 3, 4). Find its vertices.
Answer: Let A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3) be the vertices of the given triangle, and let D(1,5,–1), E(0,4,–2) and F(2,3,4) be the mid-points of the sides BC, CA and AB respectively.
As, D is the mid-point of BC

Adding first three equations in (i), (ii) and (iii), we get,
2(x1 + x2 + x3) = 6
⇒ x1 + x2 + x3 = 3
Solving first equations in (i), (ii) and (iii) with (iv), we
get, x1 = 1, x2 = 3, x3 = –1
Adding second equations in (i), (ii) and (iii), we get,
2(y1 + y2 + y3) = 10 + 8 + 6
⇒ y1 + y2 + y3 = 12 …(v)
Solving second equations in (i), (ii) and (iii) with (v), we
get, y1 = 2, y2 = 4, y3 = 6
Adding last equations in (i), (ii) and (iii), we get,
2(z1 + z2 + z3) = –2 – 4 + 8 ⇒ z1 + z2 + z3 = 1 …(vi)
Solving last equations in (i), (ii) and (iii) with (vi),
we get, z1 = 3, z2 = 5, z3 = –7
Thus, the vertices of the triangle are A(1,2,3), B(3,4,5) and C(–1, 6, –7).
Question. Show that the points A(1, 2, 3), B(–1, –2, –1), C(2, 3, 2) and D(4, 7, 6) are the vertices of a parallelogram ABCD, but it is not a rectangle.
Answer: Given vertices are A(1, 2, 3), B(–1, –2, –1), C(2, 3, 2) and D(4, 7, 6).

Coordinates of mid-point of AC are

As mid points of AC and BD are same
So, A, B, C and D are the vertices of a parallelogram.
Now, AC = √(2 − 1)2 + (3 − 2)2 + (2 − 3)2
= √1 + 1 + 1 = 3
BD = √(4 + 1)2 + (7 + 2)2 + (6 + 1)2
= √25 + 81 + 49 = 155
As, AC ≠ BD ⇒ Diagonals are not equal.
∴ ABCD is not a rectangle
Hence, A, B, C and D are vertices of a parallelogram but not rectangle.
Question. Determine the point in XY plane which is equidistant from three points A(2, 0, 3), B(0, 3, 2) and C(0, 0, 1).
Answer: Let P be the point equidistant from three given
points. The point in XY plane is of the form P(x, y, 0).
According to question, AP = BP = CP
⇒ AP2 = BP2 = CP2
Now, AP2 = BP2
⇒ (x – 2)2 + (y – 0)2 + (0 – 3)2
= (x – 0)2 + (y – 3)2 + (0 – 2)2
⇒ x2 + 4 – 4x + y2 + 9 = x2 + y2 + 9 – 6y + 4
⇒ 6y = 4x ⇒ x = 6/4 y
Again, BP2 = CP2
⇒ (x – 0)2 + (y –3)2 + (0 – 2)2 = (x – 0)2 + (y – 0)2
+ (0 – 1)2
⇒ x2 + y2 + 9 – 6y + 4 = x2 + y2 + 1
⇒ 6y = 12 ⇒ y = 2
Put y = 2 in (i) we get, x = 6/4 x 2 = 3
∴ Required point is (3, 2, 0)
Question. Find the point in the xy-plane which is equidistant from the points (5, 0, 6), (0, –3, 2) and (4, 5, 0).
Answer: Any point in xy-plane is of the form (x, y, 0).
Let P(x, y, 0) be equidistant from A(5, 0, 6),
B(0, –3, 2) and C(4, 5, 0).
∴ PA = PB ⇒ PA2 = PB2
⇒ (x – 5)2 + (y – 0)2 + (0 – 6)2 = (x – 0)2 + (y + 3)2 + (0 – 2)2
⇒ x2 + 25 – 10x + y2 + 36 = x2 + y2 + 9 + 6y + 4
⇒ 5x + 3y = 24 …(i)
Also, PB = PC ⇒ PB2 = PC2
⇒ (x – 0)2 + (y + 3)2 + (0 – 2)2 = (x – 4)2 + (y – 5)2 + (0 – 0)2
⇒ x2 + y2 + 9 + 6y + 4 = x2 + 16 – 8x + y2 + 25 – 10y
⇒ 2x + 4y = 7 …(ii)
Solving (i) and (ii), we get, x = 75/14 and y = -13/14 .
∴ Coordinates of P are (75/14 , -13/14 ,0) .
Case Based Questions :
Case I : Read the following passage and answer the questions from 41 to 45.
Raj and his father were walking in a large park.
They saw a kite flying in the sky. The position of kite, Raj and Raj’s father are at (20, 30, 10), (4, 3, 7) and (5, 3, 7) respectively.
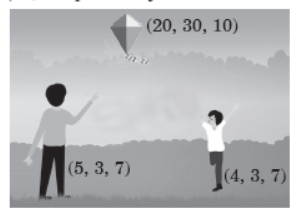
Question. The co-ordinates of Raj lie in
(a) IV quadrant
(b) III quadrant
(c) II quadrant
(d) I quadrant
Answer
D
Question. If co-ordinates of kite, Raj and Raj’s father form a triangle, then find the centroid of it.
(a) (9.67, 12, 8)
(b) (9.6, 8, 12)
(c) (12, 8, 10)
(d) (7, 9, 7.2)
Answer
A
Question. The co-ordinates of points in the XY-plane are of the form
(a) (0, 0, z)
(b) (x, y, 0)
(c) (x, 0, y)
(d) (0, x, y)
Answer
B
Question. The distance between Raj and kite is
(a) 41.32 units
(b) 31.52 units
(c) 38.32 units
(d) 40.39 units
Answer
B
Question. The distance between Raj’s father and kite is
(a) 31.30 units
(b) 38.43 units
(c) 31.03 units
(d) 29.00 units
Answer
C
Case II : Read the following passage and answer the questions from 46 to 50.
Deepak and his friends went for camping for 2 or 3 days. There they set up a tent which is triangular in shape. The vertices of the tent are A(4, 5, 9), B(3, 2, 5), C(5, 2, 5), D(–3, 2, –5) and E(–4, 5, –9) respectively.

The vertex A is tied up by the rope at the ends F and G and the vertex E is tied up at the ends I and H.
Question. If the length of the rope by which E is tied up with H is 5 √2 units, then the equation denotes the set of point of H is
(a) x2 + y2 + z2 – 8x – 10y – 18z + 72 = 0
(b) x2 + y2 + z2 – 8x – 10y – 18z – 72 = 0
(c) x2 + y2 + z2 + 8x – 10y + 18z + 72 = 0
(d) x2 + y2 + z2 + 8x + 10y + 18z + 72 = 0
Answer
C
Question. The length BC is
(a) 4 units
(b) 2 units
(c) 16 units
(d) 8 units
Answer
A
Question. The octant in which D lies is
(a) II
(b) III
(c) V
(d) VI
Answer
D
Question. If M denotes the position of their bags inside the tent and it is just in middle of the vertices B and D, then the coordinates of M are
(a) (0, 2, 0)
(b) (3, 2, 0)
(c) (0, 2, 5)
(d) (3, 2, 5)
Answer
A
Question. The length AE is
(a) √97 units
(b) 2 √97 units
(c) 3 √97 units
(d) 4 √97 units
Answer
B
Case III : Read the following passage and answer the questions from 51 to 55.
Ravi makes a plan to gift his friend a hand made pen-stand of the trapezoidal shape given in the figure :
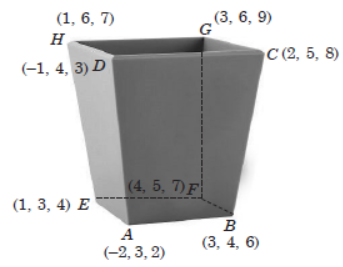
The vertices of the pen-stand are A(–2, 3, 2),
B(3, 4, 6), C(2, 5, 8), D(–1, 4, 3), E(1, 3, 4)
F(4, 5, 7), G(3, 6, 9) and H(1, 6, 7).
Question. Find the coordinates of the point which divides the line segment EH in 2 : 1.
(a) (1, 3, 6)
(b) (1, 5, 6)
(c) (1, 4, 6)
(d) (1, 2, 6)
Answer
B
Question. The length of foot of perpendicular drawn from C on y-axis is
(a) (2, 0, 0)
(b) (0, 5, 0)
(c) (0, 0, 8)
(d) (2, 5, 0)
Answer
B
Question. The ratio in which the line segment joining the vertices E and F is divided by yz-plane externally is
(a) 1 : 3
(b) 1 : 2
(c) 1 : 4
(d) 4 : 1
Answer
C
Question. The points A, B, E and F are the vertices of
(a) Parallelogram
(b) Rhombus
(c) Isoseles trapezium
(d) None of these.
Answer
D
Question. If I and J are the mid-point of AB and EF respectively, then the length of IJ is
(a) √2 units
(b) √3 units
(c) √26 / 2 units
(d) √7 units
Answer
C

