Please refer to Limits and Derivatives Class 11 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 11 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 11 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 11.
Class 11 Mathematics Important Questions Limits and Derivatives
Assertion & Reasoning Based MCQs :
(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.
Question. Assertion : The derivative of y = 2x-3/4 is 2.
Reason : The derivative of y = cx is c.
Answer
A
Question. Assertion : The derivative of h(x) = x+cos x/tan x is (1-sin x) tan x-(x+cos x) sec2 x./(tanx)2
Reason : (u/v)’= u’v-uv/(v)2
Answer
A
Question. Let u = f(x) and v = g(x). Then, Assertion : (uv)′ = u′v + uv′ is a Leibnitz rule or product rule.
Reason : (u/v)’= u’v-uv/v’ is a Leibnitz rule or quotient rule.
Answer
C
Question. Assertion : The derivative of f(x) = x3 is x2.
Reason : The derivative of f(x) = xn is nxn – 1
Answer
D
Case Based Questions :
Case I : Read the following passage and answer the questions from 32 to 36.
Let f be a real valued function, the function defined by f ′(x) = lim h→0 f(x+h) – f(x)/h whenever the limit exists is defined to be the derivative of f at x.
For a function f(x) = tan x, answer the following questions.
Question. The value of lim h→0 f(x+h) – f(x)/h is
(a) cos2x
(b) tan x
(c) 1/cos2 x
(d) 1
Answer
C
Question. The value of f ′(0) is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
Question. Find the value of f ′(60°).
(a) √3
(b) 2
(c) 4
(d) 6 √3
Answer
C
Question. The value of f(x + h) is
(a) sin (x + h)
(b) tan2 (x + h)
(c) tan (x + h)
(d) tan (x – h)
Answer
C
Question. The value of f(x + h) – f(x) is
(a) sin h/cos(x+h)cos x
(b) tan h/cos(x+h)cos x
(c) cos h/sin(x+h)cos x
(d) cos(x+h)cos x/sin(x+h)
Answer
A
Case II : Read the following passage and answer the questions from 37 to 41.
Let f(x) = anxn + an – 1 x n – 1 + …… + a1x + a0 be a polynomial function, where ai’s are all real numbers and an ≠ 0. Then the derivative of function f(x) is given by
d/dxf(x) = nanxn-1 + (n-1)a n-1 xn-2 + …..+ 2a2x+a1
For a function f (x) = x100/100 + x99/99 + …. + x2/2 + x+1 , answer the following questions.
Question. The value of f ′(1) is
(a) 100
(b) 0
(c) 200
(d) 10
Answer
A
Question. Which of the following condition satisfies?
(a) f ′(1) = 99 f ′(0)
(b) f ′(1) = 100 f ′(0)
(c) f ′(0) = f ′(1)
(d) f ′(0) = 100 f ′(1)
Answer
B
Question. The value of f ′(0) is always
(a) coefficient of x2 in f(x)
(b) 0
(c) constant term of f(x)
(d) None of these
Answer
C
Question. The derivative of f(x) w.r.t x is
(a) x100 + x99 + x98 + …… + x + 1
(b) x99 + x98 + …… + x + 1
(c) 100 x99 + 99×98 + …… + x + 1
(d) None of these.
Answer
B
Question. The value of f ′(0) is
(a) 2
(b) 0
(c) 1
(d) –1
Answer
C
Case III : Read the following passage and answer the questions from 42 to 46.
Let f and g be two functions such that their derivatives are defined in a common domain. We define the derivative of product of two functions is given by the product rule i.e.,
d/dx[f(x) . g(x)] = g(x) d/dx f(x) + f(x) . d/dx g(x)
The derivative of quotient of two functions is given by quotient rule i.e.,
d/dx[f(x)/g(x)] = g(x)d/dxf(x) – f(x) . d/dxg(x)/(g(x))2 ; g(x) ≠ 0
Question. The value of d/dx (x=1/x-1) is
(a) (x – 1)2
(b) -2/(x-1)2
(c) 1/(x-1)2
(d) -1(x-1)2
Answer
B
Question. Find the value of derivative of x2cos π/4/sin x at x =π/2 .
(a) π/2
(b) 1/√2
(c) π/√2
(d) π/3
Answer
C
Question. The product rule given above is also referred as
(a) Sandwich theorem
(b) Leibnitz product rule
(c) Chain rule
(d) None of these
Answer
B
Question. Find the derivative of x(x + 2).
(a) x + 2
(b) 2x + 1
(c) 3x + 4
(d) 2(x + 1)
Answer
D
Question. The value of f ′(x), if f(x) = sin x⋅ cos x is
(a) cos 2x
(b) sin 2x
(c) 1
(d) cos x
Answer
A
Very Short Answer Type Questions :
Question. Find the derivative of x3sec x w.r.t. x.
Answer: d/dx(x3 sec x) = x3.d/dx(sec x) + sec x . d/dx (x3)
= x3. sec x tan x + sec x. 3×2
= x2 secx (x tanx + 3)
Question. Differentiate f (x) = (3x + 5)(1 + tan x) with respect to x.
Answer: We have, f(x) = (3x + 5) (1 + tanx)
f'(x) = d/dx [(3x + 5) (1 + tanx)]
= (3x + 5) d/dx (1 + tan x) + (1 + tan x) d/dx (3x + 5)
= (3x + 5) (sec2x) + (1 + tanx) (3)
= 3xsec2x + 5 sec2x + 3 + 3 tanx
= 3(1 + tanx + x sec2x) + 5 sec2 x.
Question. Find the derivative of x–3(5 + 3x).
Answer: Let y = x–3 (5 + 3x)
⇒ y = 5.x–3 + 3x–2
∴ dy/dx = 5(-3).x-4 + 3(-2).x-3
= – 15x–4 – 6x–3
= – 3x–3 (5x–1 + 2)
∴ dy/dx = -3/x3 (5/x+2) = -3/x4(5+2x)
Question. Write the derivative of x2tanx w.r.t. x.
Answer: We have, d/dx (x2.tan x)
= x2 d/dx(tann x ) + tanx . d/dx(x2)
= x2 · sec2x + tanx·(2x)
= x(x· sec2x + 2tanx) .
Question. Find the derivative of f (x) = cosx – sinx at x = 2π/3 .
Answer: We have, f(x) = cosx – sinx
⇒ f ‘(x) = d/dx (cosx) – d/dx (sin x) = – sinx – cosx
∴ f'(2π/3) = -(sin 2π/3 + cos 2π/3)
= −(√3/2 – 1/2)
∴ f'(2π/3) = 1-√3/2
Question. Evaluate : d/dx(sec2 x) .
Answer: d/dx (sec2 x) = d/dx (secx secx)
= secx .(secx tanx) + secx(secx tanx)
∴ d/dx (sec2 x) = 2sec2 x tanx
Question. Find the derivative of x3 − 3x2 +2x−4
Answer: d/dx(x3-3x2+2x-4)
= d/dx(x3) – 3 d/dx (x2) + 2 d/dx(x-4)
= 3x2 −3 × 2x + 2 (−4x−5 )
= 3x2 −6x−8x−5
Question. Differentiate (√x+1/√x)2 w.r.t. x.
Answer: We have, d/dx (√x + 1/√x)2
= d/dx(x+1/x+2)
= d/dx(x) + d/dx(1/x) + d/dx(2)
= 1+(-1/x2) + 0 = 1 – 1/x2
Question. Write the derivative of x3sinx w.r.t. x.
Answer: Let f(x) = x3 sinx
⇒ f'(x) = d/dx (x3 sin x) = 3x2 . sinx + x3 cosx
= x2 (3 sinx + x cosx)
Question. Differentiate f(x) = x3+x2+x1/x with respect to x.
Answer: f (x) = x3+x2+1/x = x2+x+1/x
∴ f'(x) = d/dx(x)2 + d/dx(x) + d/dx(1/x)
= 2x +1− 1/x2 = 2×3+x2-1/x2
Short Answer Type Questions :
Question. Find the derivative of f (x) = cosx using first principle.
Answer: Given, f(x) = √cos x
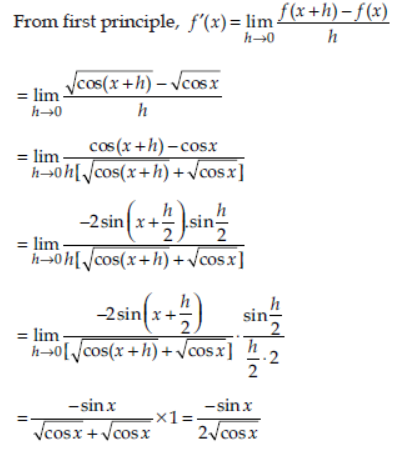
Question. If f(x) = 1 – x + x2 – x3 … –x99 + x100, then find f ′(1)⋅
Answer: We have,
f(x) = 1 – x + x2 – x3 + …… – x99 + x100
⇒ f ′(x) = 0 – 1 + 2x – 3×2 + …… – 99×98 + 100×99
= – 1 + 2x – 3×2 + ….. – 99×98 + 100×99
Now, for x = 1, f ′(1) = – 1 + 2 – 3 + ….. –99 + 100
= (–1 – 3 – 5 – ….. – 99) + (2 + 4 + ….. + 100)
= – 50/2[(2 x 1) + (50-1)2] + 50/2 [(2 x 2) + (50-1)2]
= – 25 [2 + 49 × 2] + 25[4 + 49 × 2]
= – 25 (2 + 98) + 25 (4 + 98) = – 2500 + 2550 = 50
Question. For the function f, given by f (x) = x2 – 6x + 8, prove that f'(5) – 3f'(2) = f'(8).
Answer: We have, f (x) = x2 – 6x + 8 ⇒ f'(x) = 2x – 6
⇒ f'(5) = 10 – 6 = 4; f'(2) = 4 – 6 = – 2;
f'(8) = 16 – 6 = 10.
∴ f ′(5) – 3f ′(2) = 4 – 3 (– 2) = 10 = f ′(8)
Question. Find the derivative of f (x) = (ax2 + sin x) (p + qcosx)
Answer: Given, f(x) = (ax2 + sin x)(p + qcosx)
f'(x) = d/dx {(ax2 + sinx)(p + q cosx)}
= (ax + sinx) . d/dx (p+q cos x) + (p+q cos x) . d/dx(ax2 + sin x)
= (ax2 + sinx).(–q sinx) + (p + q cosx).(2ax + cosx)
= –aqx2sinx – qsin2x + 2apx + pcosx + 2aqx cos x
+ q cos2x
Question. Find the derivative of f(x) = 10x using first principle.
Answer: Given, f(x) = 10x
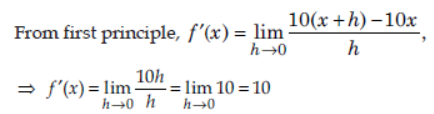
Question. Find the derivative of the following functions :
(i) 5 sin x – 6 cos x + 7
(ii) 3 cot x + 5 cosec x
(iii) 2 tan x – 7 sec x.
Answer: (i) Let f(x) = 5 sin x – 6 cos x + 7 … (1)
Differentiating (1) with respect to x, we get
f ′(x) = 5 cos x – 6 (– sin x) + 0
∴ f ′(x) = 5 cos x + 6 sin x.
(ii) Let f(x) = 3 cot x + 5 cosec x … (1)
Differentiating (1) with respect to x, we get
⇒ f ′(x) = – 3 cosec2 x – 5 cot x · cosec x
= – cosec x [3 cosec x + 5 cot x].
(iii) Let f(x) = 2 tan x – 7 sec x … (1)
Differentiating (1) with respect to x, we get
f ′(x) = 2 sec2 x – 7 sec x tan x
Question. Find the derivative of 1/ax2+b , with respect to x.
Answer: Let y = 1/ax2 + b
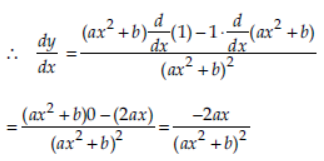
Question. Find the derivative of 3x+4/5×2 – 7x + 9 .
Answer: Let y = 3x+4/5×2 – 7x + 9
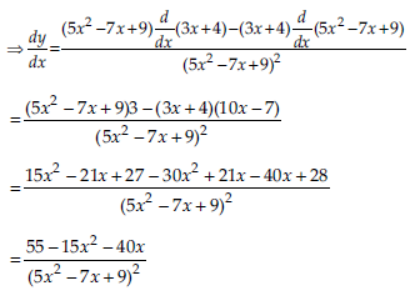
Question. Find the derivative of
(i) (6×3 + 9x)(5x + 10) (ii) 5x+4/x-3 .
Answer: (i) We have, d/dx[(6×3 + 9x)(5x+10)]
= d/dx{30×4 + 60×3 + 45×2 + 90x)
= 30 × 4×3 + 60 × 3×2 + 45 × 2x + 90 × 1
= 120×3 + 180×2 + 90x + 90
= 30 (4×3 + 6×2 + 3x +3)

Question. Differentiate : a+b sin x/c+d cos x .
Answer: Let y = a+b sin x/c+d cos x


Question. Find the derivative of y = x+sin x/(x2 – 1) .
Answer: We have, y = x+sin x/(x2-1) ⇒ dy/dx = d/dx {x+sin x/x2-1}

Question. Find f′(x) using first principle, where f(x) = x-1/x .
Answer: Given, f(x) = x – 1/x
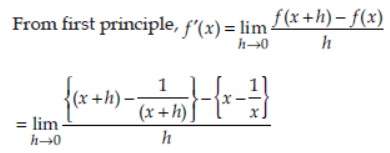

Question. Differentiate 2×3- sin x/cot x w.r.t. x.
Answer: Let y = 2×3 – sin x/cot x
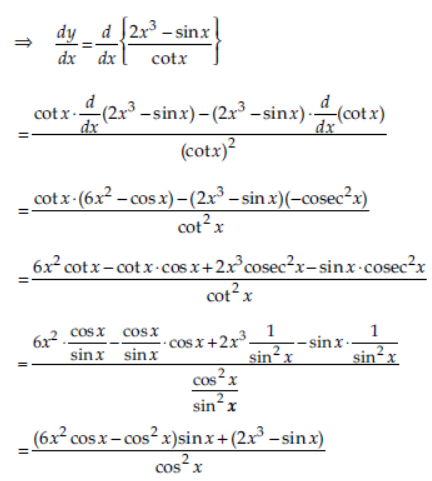
Question. Differentiate tan2x using first principle.
Answer: Let f(x) = tan2x
∴ By first principle of differentiation, we have,

Question. Find the derivative of cos x using first principle.
Answer: Let f (x) = cos x
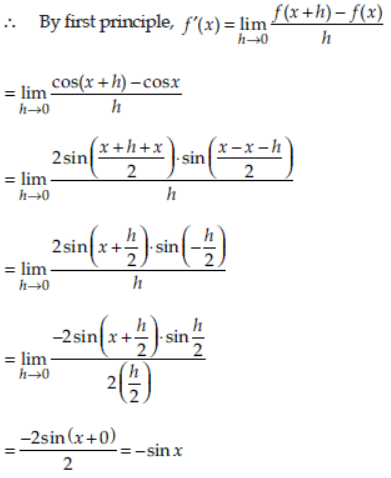
Question. If y = sin x + cos x/sin x -cos x , then find the value of dy/dx at x = 0.
Answer: We have, y = sin x + cos x/sin x -cos x
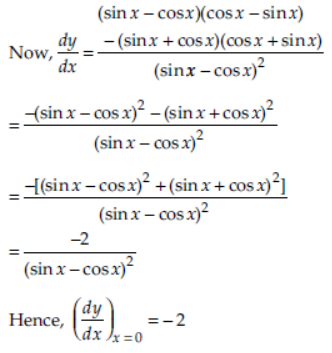
Question. Find the derivative of tan(2x + 3) by first principle method.
Answer: Let f (x) = tan (2x + 3)
Then, using first principle

Question. Find the derivative of x5(3 – 6x–9) with respect to x.
Answer: d/dx{x5(3-6x-9)} = d/dx {3.x5 – 6x-4}
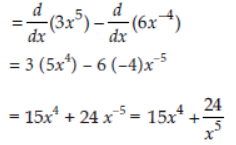
Question. Find the derivative of sin 2x by first principle.
Answer: Let f(x) = sin2x
Then, using first principle,
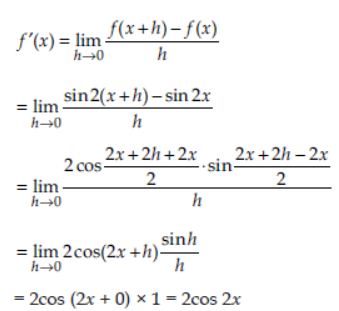
Question. Differentiate f(x) = 3-x/3+4x with respect to x by first principle of derivative.
Answer: Here, f(x) = 3-x/3+4x
From first principle,
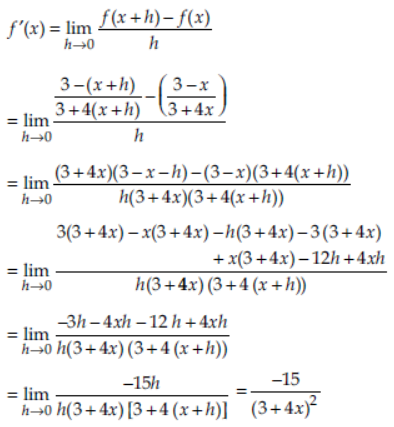
Question. Differentiate x2/3 by using first principle.
Answer: Let f(x) = x2/3

Question. Using the method of first principle find the derivative of f (x) = 2x+7/x+2 .
Answer: Here, f(x) = 2x+7/x+2
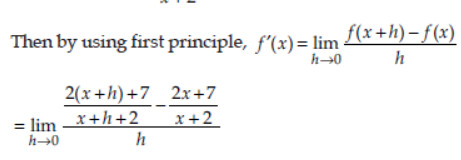
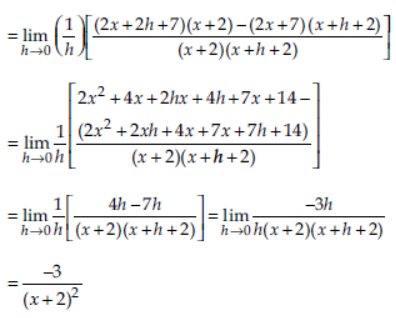
Question. Find the derivative of √1+sin x/√1-sin x .
Answer: Let y = √1+sin x/√1-sin x = √(1+sin x)2/1-sin2 x
= 1+sin x/cos x = sec x + tan x
Now dy/dx = d/dx (secx + tanx) = sec x tan x + sec2x
Question. If f (x) = (cos x/2 + sin x/2)2 , then find f'(π/4) .
Answer: f(x) = (cos x/2 + sin x/2)2
= cos2 x/2 + sin2 x/2 + 2sin x/2 cos x/2
⇒ f(x) = 1 + sin x
⇒ f ′(x) = 0 + cos x = cos x
∴ f'(π/4) = cos π/4 = 1/√2
Question. Differentiate : 4x+5 sin x/3x + 7 cos x .
Answer: Let f(x) = 4x+5 sin x/3x + 7 cos x
Differentiating (i) with respect to x, we get

Long Answer Type Questions :
Question. If f(x) = xn-an/x-a for some constant ‘a’, then prove that f ′(a) does not exists.
Answer: We have, f(x) = xn-an/x-a

Therefore, f ′(a) does not exist.
Because, f(x) is not defined at x = a.
So, f ′(x) at x = a does not exist.
Question. (i) Find the derivative of cot x using first principle method.
(ii) Find the derivative of f (x) = x/1+tan x .
Answer: (i) Consider f(x) = cot x

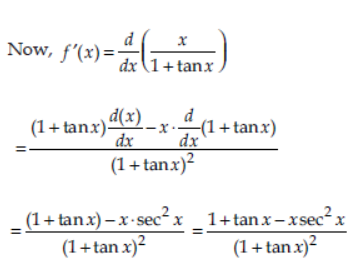
Question. Find the derivative of cosec x with respect to x, from first principle.
Answer: Let f(x) = cosec x


Question. Differentiate cot √x w.r.t. x from first principle method.
Answer: Let f (x) = cot √x
From first principle,
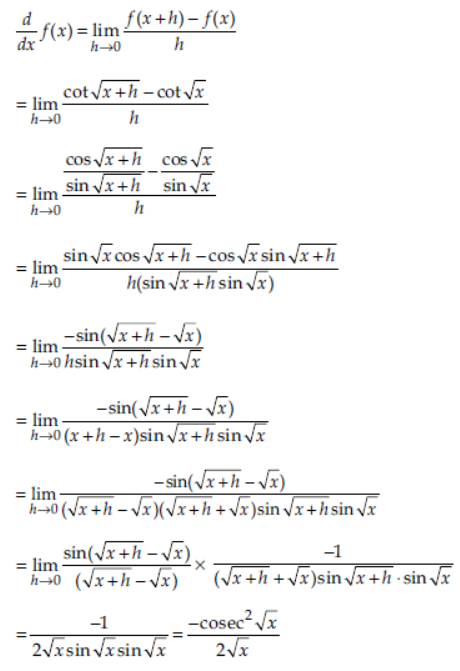
Question. Find the derivative of sin x + cos x from first principle.
Answer: Let f (x) = sinx + cosx


