Please refer to Quadrilaterals Class 9 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 9 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 9 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 9.
Class 9 Mathematics Important Questions Quadrilaterals
Short Answer Type Questions:
Question. Two opposite angles of a parallelogram are (3x – 2)°and (63 – 2x)°. Find all the angles of a parallelogram.
Ans. Since, opposite angles of a parallelogram are equal.
∴ 3x – 2 = 63 – 2x or 5x = 65
or, x = 13° 1
Angles of the parallelogram are :
(39 – 2)°, (180 – 37)°, (63 – 26)° and (180 – 37)°
i.e., 37°, 143°, 37° and 143°.
Question. In the given parallelogram ABCD, two points P and Q are taken on the diagonal BD such that DP = BQ. Show that :
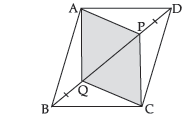
(i) ΔAPD ≅ ΔCQB
(ii) ΔAQB ≅ ΔCPD
(iii) APCQ is a parallelogram A
Ans. (i) In ΔAPD and ΔCQB
AD = BC (Opp. sides of a parallelogram)
PD = QB (Given)
∠ADP = ∠CBQ (Alt. Angles)
So, ΔAPD ≅ ΔCQB (SAS Rule)
or, AP = CQ, DP = BQ (c.p.c.t.)
(ii) In ΔAQB and ΔCPD
AB = DC (opp. sides of parallelogram)
BQ = DP (proved above)
and ∠ABQ = ∠PDC (Alt. angles)
∴ ΔAQB ≅ ΔCPD or, AQ = CP (c.p.c.t.)
(iii) In quad. APCQ,
AP = CQ and AQ = CP (Proved above)
∴ APCQ is a ||gm Hence Proved.
Question. PQRS is a quadrilateral with SQ as one of its diagonals. If SR = PQ = 4 cm, SQ = 5 cm and SQ is perpendicular to both SR and PQ, show that ar (ΔPSQ) = ar (ΔSRQ).
Ans.
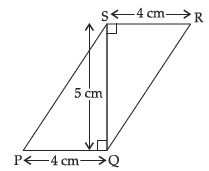
In ΔPSQ and ΔRQS,
PQ = SR (Each 4 cm)
SQ = SQ (common)
∠SQP =∠QSR (Each 90°, given)
∴ ΔPSQ ≅ ΔRQS by SAS rule.
Thus, ar(ΔPSQ) = ar(ΔSRQ) [Areas of congruent figures are equal.] Hence Proved
Question. ABCD is a quadrilateral in which P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that PQRS is a parallelogram.
Ans. Join diagonal AC.
In ΔADC,
S is the mid-point of AD.
R is the mid-point of DC.
∴ SR || AC
and SR = 1/2 AC (By mid-point theorem) …(i)
Similarly in ΔBAC,
PQ || AC
and PQ = 1/2 AC …(ii)
From (i) and (ii),
SR || PQ
and SR = PQ
∴ PQRS is a parallelogram. Hence Proved
Question. ABCD is a parallelogram. If E is mid-point of BC and AE is the bisector of ∠A, prove that AB = 1/2 AD.
Ans. Here, ∠1 = ∠2 (AE is the angle bisector)
But, ∠1 = ∠3 (alternate angles as AD || BC)
⇒ ∠3 = ∠2
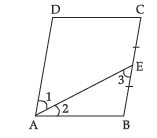
Hence, BE = AB (Sides opposite to equal angles)
But, BE = 1/2 BC (E is the mid-point of BC)
∴ AB = 1/2 BC
Also, BC = AD (opposite sides of a parallelogram)
∴ AB = 1/2 AD. Proved.
Question. PQRS is a parallelogram and PL and RM are perpendiculars drawn from the vertices P and R of the parallelogram on diagonal SQ. Show that
(i) ΔPQL ≅ ΔRMS (ii) PL = RM
Ans. (i) In ΔRSM and ΔPQL,
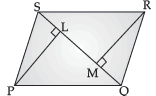
∠RSM = ∠PQL (Alternate interior angles)
∠M = ∠L (90° each)
SR = PQ (Parallel sides of parallelogram are equal)
By AAS, ΔRSM ≅ ΔPQL
(ii) PL = RM (c.p.c.t.)
Hence Proved.
Question. In a parallelogram, show that the angle bisectors of two adjacent angles intersect at right angle.
Ans. ∠ADC + ∠BCD = 180°
or, 1/2 ∠ADC + 1/2 ∠BCD = 90°
or ∠1 + ∠2 = 90°

In ΔODC,
∠1 + ∠2 + ∠DOC = 180°
∴ ∠DOC = 90°
Question. D, E and F are the mid-points of sides PQ, QR and RP respectively of an equilateral ΔPQR. Show that ΔDEF is also an equilateral triangle.
Ans.
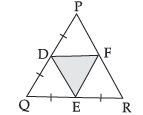
DE || PR and DE = 1/2 PR (By mid-point theorem)
EF || PQ and EF = 1/2 PQ
DF || QR and DF = 1/2 QR
As PQ = QR = PR (PQR is an equilateral triangle)
or, DE = EF = DF
or, ΔDEF is an equilateral triangle. Hence Proved
Question. In given figure, ABCD is a parallelogram. P, Q are the mid-points of AB and DC. Show that :
(i) APCQ is a parallelogram.
(ii) DPBQ is a parallelogram.
(iii) PSQR is a parallelogram.

Ans. (i) Since, ABCD is a parallelogram
∴ AB = CD and AB || CD
or, 1/2 AB = 1/2 CD
i.e. AP = CQ and AP || CQ
or, APCQ is a parallelogram. Proved.
(ii) Again, 1/2 AB = 1/2 CD
i.e. PB = DQ and PB || DQ
or, DPBQ is a parallelogram. Proved.
(iii) QS || PR and SP || QR
or, PSQR is a parallelogram. Proved.
Question. In the figure, ABCD is a parallelogram and E is the mid-point of side BC. DE and AB on producing meet at F. Prove that AF = 2AB.
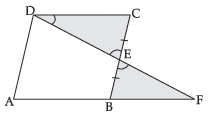
Ans. CE = BE (Given)
In ΔDCE and ΔFBE,
∠DCE = ∠FBE (alternate interior angles)
CE = BE (Given)
∠DEC = ∠BEF (V.O.A.)
ΔDCE ≅ ΔFBE (A.S.A.)
or, DC = FB (c.p.c.t.)
or, AF = AB + BF = AB + AB = 2AB
Hence Proved.
Question. Prove that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
OR
ABCD is a rectangle and P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Ans.
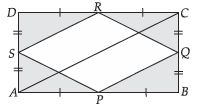
In ΔABC, P and Q are mid points of AB and BC respectively.
∴ PQ = 1/2 AC and PQ || AC … (i)
Similarly, RS = 1/2 AC and RS || AC …(ii)
∴ PQRS is a parallelogram
Also, AD= BC or, AS = BQ
In ΔAPS and ΔBPQ,
AP = BP, AS = BQ and ∠A = ∠B = 90° 1
∴ ΔAPS ≅ ΔBPQ (SAS Congruency)
or, PS = PQ …(iii)
Hence, PQRS is a parallelogram with PQ = PS
i.e., PQRS is a rhombus. Hence Proved.
Question. Prove that the diagonals of a rectangle are equal in length.
Ans. Let PQRS be a rectangle.
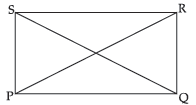
In ΔSPQ and ΔRQP,
SP = RQ, (Opp. sides of rectangle are equal)
∠SPQ = ∠RQP = 90° (Each angle of rectangle is right angle)
PQ = QP (Common)
ΔSPQ ≅ ΔRQP (SAS Congruence Rule)
QS = PR (c.p.c.t.) Hence Proved.
Question. In ΔABC, D, E and F are the mid-points of sides AB, BC and CA. If AB = 6 cm, BC = 7·2 cm and AC = 7·8 cm, find the perimeter of ΔDEF.
Ans. DE = 1/2 AC
EF = 1/2 AB
DF = 1/2 BC (By Mid-point theorem)
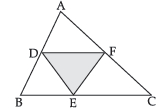
Perimeter of DEF = DE + EF + DF
= 1/2 (AC +AB + BC)
= 1/2 (7·8 + 6 + 7·2)
= 1/2 (21)
= 10·5 cm
Long Answer Type Questions :
Question. If ΔABC and ΔDEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF then show that :
(i) quadrilateral ABED is a parallelogram.
(ii) quadrilateral BCFE is a parallelogram.
(iii) AC = DF
(iv) ΔABC ≅ ΔDEF.
Ans. Given : Two triangles ABC and DEF, such that
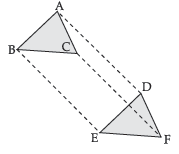
AB = DE and AB || DE
Also, BC = EF and BC || EF
Proof: (i) In a quadrilateral ABED,
AB = DE and AB II DE
i.e., one pair of opposite sides are equal and parallel.
∴ ABED is a parallelogram. Proved.
or, AD = BE and AD || BE. …(i)
(ii) In quadrilateral BCFE,
BC = EF and BC || EF
i.e., one pair of opposite sides are equal and parallel.
∴ BCFE is a parallelogram. Proved.
or, CF = BE and CF || BE. ….(ii)
(iii) From equations (i) and (ii), we get
AD= CF and AD || CF
or, ACFD is a parallelogram.
or, AC = DF and AC || DF
(iv) In ΔABC and ΔDEF,
AB = DE (Given)
BC = EF (Given)
and AC = DF (Proved above in part (iii))
So by SSS rule ΔABC ≅ ΔDEF. Hence Proved
Question. Show that the bisectors of angles of a parallelogram enclose a rectangle.
OR
Show that the bisectors of angles of a parallelogram form a rectangle.
Ans. Let ABCD is a parallelogram.
AN, BN, CL and DL are bisectors of ∠A, ∠B, ∠C, ∠D respectively
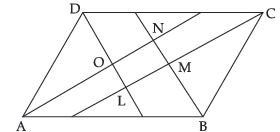
∴ AB || DC [ABCD is a parallelogram]
and AD is transversal.
∴ ∠BAD + ∠ADC = 180° [co-interior angles]
⇒ 1/2 ∠BAD + 1/2 ∠ADC = 1/2 ×180°
⇒ ∠DAO + ∠ADO = 90° …(i) [AN and DL are bisectors of ∠A and ∠D]
Now, In ΔADO,
∠DAO + ∠ADO + ∠AOD = 180° [angle sum property of triangle]
⇒ ∠AOD = 90° [from (i)]
Lines AN and DL intersect
∴ ∠LON = ∠AOD = 90°
Similarly, ∠OLN = ∠LMN
= ∠MNO = 90°
∴ Both pairs of opposite angle of LMNO are equal.
∴ LMNO is a parallelogram
∴ LMNO is a parallelogram in which one angle is 90°.
∴ LMNO is a rectangle. Hence Proved.
Question. Prove that the diagonals of a square are equal and perpendicular to each other.
Ans. Given a square ABCD in which diagonal AC and BD intersects at O.
To Prove :
AC = BD and AC ⊥ BD
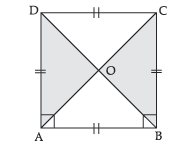
Proof : In ΔADB and ΔBCA,
AD = BC (Sides of a square)
∠BAD = ∠ABC (90° each)
AB = BA (Common)
∴ ΔADB ≅ ΔBCA (SAS)
Therefore, AC = BD (c.p.c.t.)
In ΔAOB and ΔAOD,
OB = OD,
AB = AD,
AO = AO
∴ ΔAOB ≅ ΔAOD (By SSS)
∠AOB = ∠AOD (c.p.c.t.)
Since, ∠AOB + ∠AOD = 180° (Linear pair)
∴ ∠AOB = ∠AOD = 90°
AO ⊥ BD, AC ⊥ BD
Hence, AC = BD and AC ⊥ BD. Hence Proved.
