Please refer to Circle Class 9 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 9 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 9 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 9.
Class 9 Mathematics Important Questions Circle
Very Short Answer Type Questions:
Question. If O is the centre of the circle, then find the value of x in the given figure.
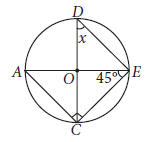
Ans. In ΔACE,
∠ACE = 90° (Angle in a semi circle)
Now, ∠CAE + ∠ACE + ∠AEC = 180°
⇒ ∠CAE + 90° + 45° = 180°
⇒ ∠CAE = 180° – 135° = 45°
Also, ∠CDE = ∠CAE = 45°
(Angles in same segment are equal)
∴ x = 45°
Question. Two chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB.
Show that l bisects CD.
Ans. We know that the perpendicular bisector of any chord of a circle always passes through the centre of the circle. Since l is the perpendicular bisector of AB. Therefore, l passes through the
centre of the circle. But l ⊥ AB and AB || CD ⇒ l ⊥ CD.
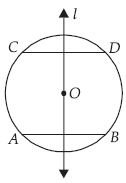
Thus l ⊥ CD and passes through the centre of the circle.
So, l is the perpendicular bisector of CD also.
Question. In the given figure, if ∠POQ = 80°, then find ∠PAQ and ∠PCQ.

Ans. We know that, the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
∴ ∠PAQ = ∠PCQ =1/2 ∠POQ = 1/2 × 80° = 40°
Question. In a cyclic quadrilateral ABCD, if ∠A = 3∠C. Find ∠A.

Ans. Since ABCD is a cyclic quadrilateral.
∴ ∠A + ∠C = 180°
⇒ 3∠C + ∠C = 180° ⇒ ∠C = 45°
∴ ∠A = 3 × 45° = 135°
Question. In the given figure, O is the centre of the circle, ∠AOC = 45° and ∠COB = 35°. Find the measure of ∠ADB.
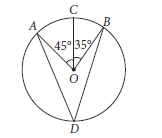
Ans. ∠AOB = ∠AOC + ∠COB
= 45° + 35° = 80°
Now, 2∠ADB = ∠AOB
(Angle subtended at centre is double the angle subtended at remaining part of the circle)
⇒ 2∠ADB = 80° ⇒ ∠ADB = 40°
Short Answer Type Questions:
Question. In the given figure, AB is a diameter of the circle with centre O. If AC and BD are perpendicular on a line PQ, and BD meets the circle at E, prove that AC = ED.
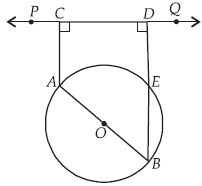
Ans. Join AE.
Now, ∠AEB = 90°
[Angle in a semicircle]
But, BED being a straight line,

we have,
∠AEB + ∠AED = 180°
⇒ 90° + ∠AED = 180°
⇒ ∠AED = 90°
Now, ∠EAC + ∠ACD + ∠CDE + ∠AED = 360°
[Sum of the angles of quadrilateral EACD is 360°]
⇒ ∠EAC + 90° + 90° + 90° = 360°
⇒ ∠EAC = 90°
Thus, each angle of quadrilateral EACD is 90°
So, EACD is a rectangle.
∴ AC = ED [Opposite sides of a rectangle].
Question. In the given figure, chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 25°.
If ∠DEC = 1/k × 455°, then find the value of k.
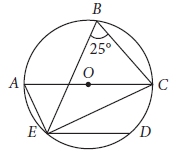
Ans. Consider the arc CDE. We find that ∠CBE and CAE are the angles in the same segment of arc CDE.
∴ ∠CAE = ∠CBE
⇒ ∠CAE = 25° [Q ∠CBE = 25°]
Since AC is the diameter of the circle and the angle in a semi-circle is a right angle. Therefore, ∠AEC = 90°.
Now, in ΔACE, we have
∠ACE + ∠AEC + ∠CAE = 180°
⇒ ∠ACE + 90° + 25° = 180° ⇒ ∠ACE = 65°
But ∠DEC and ∠ACE are alternate angles, because AC || DE.
∴ ∠DEC = ∠ACE = 65°
⇒ (1/k) × 455° = 65° ⇒ k = 7
Question. In the given figure, A, B, C and D, E, F are two sets of collinear points. Prove that AD || CF.
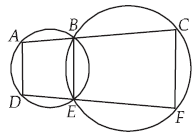
Ans. In order to prove that
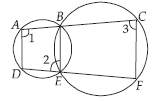
AD || CF, it is sufficient to prove
that ∠1 + ∠3 = 180°
Since ABED is a cyclic
quadrilateral.
∴ ∠1 + ∠2 = 180° …(i)
Now, BCFE is a cyclic quadrilateral and in a cyclic quadrilateral an exterior angle is equal to the interior opposite angle.
∴ ∠2 = ∠3 …(ii)
From (i) and (ii), we get ∠1 + ∠3 = 180°
Hence, AD || CF
Question. Prove that the mid-point of the hypotenuse of a right triangle is equidistant from its vertices.
Ans. Let ΔABC be a right triangle such that ∠BAC = 90°.
Let O be the mid-point of the hypotenuse BC.
Then, OB = OC.
With O as centre and OB as radius, draw a circle. Clearly this circle passes through the points B and C. If possible, suppose this circle does not pass through A. Let it meet BA produced at A′. Then,
∠BA′C = 90° ( Angle in a semicircle is 90°)
But, ∠BAC = 90°
∴ ∠BA′C = ∠BAC
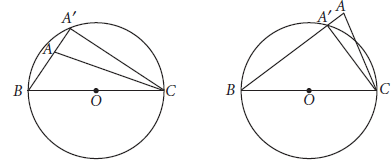
This is not possible, because an exterior angle of a triangle can never be equal to its interior opposite angle.
Thus, ∠BA′C = ∠BAC ⇒ A′ coincides with A
So, the circle which passes through B and C also passes through A.
Consequently, OA = OB = OC = radius of the circle.
Hence, the mid-point O of the hypotenuse BC of right triangle ABC is equidistant from its vertices.
Question. In the given figure, O is the centre of the circle and the measure of ∠ABC is 130°.
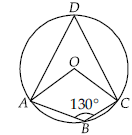
Find the value of (∠AOC − ∠ADC ) /25°
Ans. ∴ ABCD is a cyclic quadrilateral
∴ ∠ABC + ∠ADC = 180°
⇒ 130° + ∠ADC = 180° ⇒ ∠ADC = 50°
Since, angle subtended by arc at centre is double the angle subtended by it at any point on the remaining part of circle.
∴ ∠AOC = 2∠ADC = 100°
Now, ∠AOC – ∠ADC / 25° = (100° – 50°) / 25° = 50° / 25° = 2
Question. In the given figure, O is the centre of the circle and ∠DAB = 50°. Find the values of x and y.
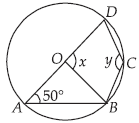
Ans. ABCD is a cyclic quadrilateral.
∴ 50° + y = 180°
⇒ y = 130°
Clearly, ΔOAB is an isosceles triangle with OA = OB.
∴ ∠OBA = ∠OAB = 50°
⇒ ∠AOB = 180° – (50° + 50°) = 80°
Hence, x = 180° – 80° = 100°
Question. A chord of circle of radius 12.5 cm with centre O is of length 15 cm. Find its distance (in cm) from the centre.
Ans. Let AB be the chord of length 15 cm.
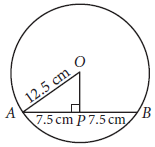
Draw OP ⊥ AB
∴ P is the mid-point of chord AB
⇒ AP = 1/2 × 15 = 7.5 cm
Now, in right angled ΔAPO,
OP2 = AO2 – AP2
= (12.5)2 – (7.5)2 = 156.25 – 56.25 = 100
∴ OP = 100 = 10 cm
Question. In the given figure, AB = CD. Prove that BE = DE and AE = CE, where E is the point of intersection of AD and BC.
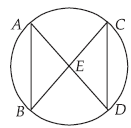
Ans. In ΔAEB and ΔCED, we have
∠BAE = ∠DCE
[Angles in the same segment]
and ∠ABE = ∠CDE
[Angles in the same segment]
Also, AB = CD
∴ ΔAEB ≅ ΔCED [By ASA congruence]
⇒ AE = CE and BE = DE [C.P.C.T.]
Question. Find the length of a chord which is at a distance of 8 cm from the centre of a circle of radius 17 cm.
Ans. Let AB be the chord of a circle of radius 17 cm.
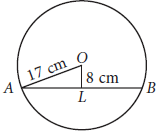
Draw OL ⊥ AB, join OA.
In right angled ΔALO
AL = √OA2 −OL2
= √172 − 82
= √289 − 64 = √225 = 15 cm
Since perpendicular from the centre to the chord bisects the chord.
∴ AB = 2AL = 2 × 15 cm = 30 cm
Question. In a ΔABC, if ∠A = 60° and the altitudes from B and C meet AC and AB at P and Q, respectively and intersect each other at I. Then, Prove that APIQ is a cyclic quadrilaterals.
Ans. ∠A = 60° (Given)
∠APB = 90° ( PB ⊥ AC)
and ∠AQC = 90° ( CQ ⊥ AB)
In quadrilateral APIQ,

∠P = 90°, ∠Q = 90°,
∠A = 60°
∴ ∠I = 360° – (90° + 90° + 60°)
= 120° …(i)
Now, we get ∠P + ∠Q = 180° and ∠A + ∠I = 180°
Hence, APIQ is a cyclic quadrilateral.
Question. In the given figure, AB is a chord of a circle with centre O and BOC is a diameter. If OD ⊥ AB such that OD = 6 cm, then the value of AC is k × 3. Find the value of k.
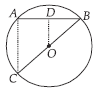
Ans. OD ⊥ AB ⇒ D is the midpoint of AB.
Also, O is the midpoint of BC.
Now, in ΔBAC, D is the midpoint of AB
and O is the midpoint of BC.
∴ By midpoint theorem,
OD =1/2 AC ⇒ AC = 2 × OD = (2 × 6) cm = 12 cm.
Now, AC = k × 3
⇒ 12 = k × 3 ⇒ k = 4 cm
Question. Prove that any angle subtended by a minor arc in the alternate segment is acute and any angle subtended by a major arc in the alternate segment is obtuse.
Ans. We known that, the angle subtended by an arc of a circle at its centre is twice the angle subtended by it at any point on the remaining part of the circle.
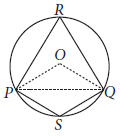
Since, PSQ is a minor arc and ∠PRQ is the angle formed by it in alternate segment.
∴ 2∠PRQ = ∠POQ
⇒ 2∠PRQ < 180° [Since, ∠POQ is an angle of ΔPOQ]
⇒ ∠PRQ < 90°
So, ∠PRQ is an acute angle.
Now, QRP is a major arc and ∠PSQ is the angle formed by it in the alternate segment.
∴ 2∠PSQ = Reflex ∠POQ
⇒ 2∠PSQ = 360° – ∠POQ
⇒ 2∠PSQ > 360° – 180° [Q ∠POQ < 180°]
⇒ ∠PSQ > 90°
Hence, ∠PSQ is an obtuse angle.
Question. Two concentric circles with centre O have A, B, C, D as the points of intersection with the line l as shown in the figure. If AD = 12 cm and BC = 8 cm, then find the lengths of AB, CD, AC and BD.

Ans. Since, OM ⊥ BC
∴ BM = CM = 1/2 BC = 4 cm [Perpendicular from the centre of a circle to a chord bisects the chord]
Similarly, OM ⊥ AD
⇒ AM = DM = 1/2 AD = 6 cm
Now, AB = AM – BM = (6 – 4) cm = 2 cm
Also, CD = DM – CM = (6 – 4) cm = 2 cm
AC = AB + BC = (2 + 8) cm = 10 cm
and BD = BC + CD = (8 + 2) cm = 10 cm
Question. D and E are points on equal sides AB and AC of isosceles ΔABC such that AD = AE. Prove that
∠DBC + ∠CED = 180°.
Ans. To prove BCED a cyclic quadrilateral, it is sufficient
to prove ∠CED + ∠DBC = 180°
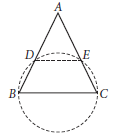
We have, AB = AC ⇒ ∠ABC = ∠ACB
Now, AD = AE ⇒ ∠ADE = ∠AED
In ΔABC,
∠A + ∠ABC + ∠ACB = 180° …(i)
In ΔADE,
∠A + ∠ADE + ∠AED = 180° …(ii)
From (i) and (ii), we have
∠A + ∠ABC + ∠ACB = ∠A + ∠ADE + ∠AED
⇒ ∠ABC + ∠ABC = ∠ADE + ∠ADE
⇒ 2∠ABC = 2∠ADE
∠ABC = ∠ADE
∴ DE || BC
∴ ∠ABC + ∠BDE = 180° (Co-interior angles)
Now, as ∠ADE = ∠AED, ∴ ∠BDE = ∠CED
⇒ ∠DBC + ∠CED = 180°
