Please refer to MCQ Questions Chapter 7 Permutations and Combinations Class 11 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 11 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 11 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 7 Permutations and Combinations in Class 11 Mathematics provided below to get more marks in exams.
Chapter 7 Permutations and Combinations MCQ Questions
Please refer to the following Chapter 7 Permutations and Combinations MCQ Questions Class 11 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 7 Permutations and Combinations Class 11 Mathematics
Question. 20 persons are invited for a party. In how many different ways can they and the host be seated at circular table, if the two particular persons are to be seated on either side of the host?
(a) 20 !
(b) 2×18 !
(c) 18 !
(d) None of these
Answer
B
Question. In how many ways can 5 boys and 5 girls sit in a circle so that no two boys sit together?
(a) 5! x 5!
(b) 4! x 5!
(c) 5! x 5!/2
(d) None of these
Answer
B
Question. How many 10-digit numbers can be written by using the digits 1 and 2 ?
(a) 10C1 + 9C2
(b) 210
(c) 10C2
(d) 10!
Answer
B
Question. The number of times the digits 3 will be written when listing the integers from 1 to 1000 is
(a) 269
(b) 300
(c) 271
(d) 302
Answer
B
Question. The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is
(a) 72
(b) 96
(c) 90
(d) 98
Answer
C
Question. A car will hold 2 in the front seat and 1 in the rear seat. If among 6 persons 2 can drive, then number of ways in which the car can be filled, is
(a) 10
(b) 20
(c) 30
(d) None of these
Answer
B
Question. Six X’s have to be placed in the square of the figure such that each row contains atleast one ‘X’. In how many different ways can this be done?
(a) 28
(b) 27
(c) 26
(d) None of these
Answer
C
Question. If nC12 nC8 = , then n is equal to
(a) 20
(b) 12
(c) 6
(d) 30
Answer
A
Question. In how many ways can a student choose a program of 5 courses, if 9 courses are available and 2 specific courses are compulsory for every student?
(a) 34
(b) 36
(c) 35
(d) 37
Answer
C
Question. Every body in a room shakes hands with everybody else. The total number of hand shakes is 66. The total number of persons in the room is
(a) 11
(b) 12
(c) 13
(d) 14
Answer
B
Question. The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is
(a) 16C11
(b) 16C5
(c) 16C9
(d) 20C9
Answer
C
Question. A box contains two white balls, three black balls and four red balls. In how many ways can three balls be drawn from the box, if atleast one black ball is to be included in the draw?
(a) 64
(b) 45
(c) 46
(d) None of these
Answer
A
Question. The number of ways in which 10 candidates A1, A2,….. A10 can be ranked such that A1 is always above A10 is
(a) 5!
(b) 2(5!)
(c) 10!
(d) 1/2 (10!)
Answer
D
Question. If eleven members of a committee sit at a round table so that the President and Secretary always sit together, then the number of arrangements is
(a) 10! x2
(b) 10!
(c) 9! x2
(d) None of these
Answer
C
Question. The number of ways in which we can choose a committee from four men and six women so that the committee includes atleast two men and exactly twice as many women as men is
(a) 94
(b) 126
(c) 128
(d) None of these
Answer
A
Question. A five digit number divisible by 3 is to be formed using the numbers 0, 1, 2, 3, 4 and 5, without repetition. The total number of ways this can be done, is
(a) 216
(b) 240
(c) 600
(d) 3125
Answer
A
Question. There are 10 lamps in a hall. Each one of them can be switched on independently. Find the number of ways in which hall can be illuminated.
(a) 210 -2
(b) 210 -1
(c) 210 +1
(d) None of these
Answer
B
Question. Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5,provided that no digit is to be repeated.
(a) 111
(b) 112
(c) 113
(d) None of these
Answer
B
Question. In an examination, a student has to answer 4 questions out of 5 questions; questions 1 and 2 are however compulsory. Find the number of ways in which the student can make the choice.
(a) 3
(b) 2
(c) 4
(d) 5
Answer
A
Question. A sports team of 11 students is to be constituted, choosing atleast 5 from Class XI and atleast 5 from Class XII. If there are 20 students in each of these classes, in how many ways can the team be constituted?
(a) 20C5 x20C6
(b) 2(20C5 x20C6)
(c) 2(20C5)2
(d) None of these
Answer
B
Question. A pack of 52 cards are shuffled together. The number of ways in which a man can be dealt 26 cards so that he does not get two cards of the same suit and same denomination, is
(a) 52C26 . 226
(b) 104C26
(c) 2. 52C26
(d) None of these
Answer
A
Question. In how many ways can 21 English and 19 Hindi books be placed in a row so that no two Hindi books are together?
(a) 1540
(b) 1450
(c) 1504
(d) 1405
Answer
A
Question. 4 buses runs between Bhopal and Gwalior. If a man goes from Gwalior to Bhopal by a bus and comes back to Gwalior by another bus, then the total possible ways are
(a) 12
(b) 16
(c) 4
(d) 8
Answer
A
Question. In a football championship, there were played 153 matches. Every team played one match with each other. The number of teams participating in the championship is
(a) 17
(b) 18
(c) 9
(d) 13
Answer
B
Question. A father with 8 children takes them 3 at a time to the zoological gardens, as often as he can without taking the same 3 children together more than once. The number of times he will go the garden, is
(a) 336
(b) 112
(c) 56
(d) None of these
Answer
C
Question. A question paper is divided into two parts A and B and each part contains 5 questions. The number of ways in which a candidate can answer 6 questions electing atleast two questions from each part is
(a) 80
(b) 100
(c) 200
(d) None of these
Answer
C
Question. In an examination there are three multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answers correct, is
(a) 11
(b) 12
(c) 27
(d) 63
Answer
D
Question. There were two women participating in a chess tournament. Every participant played two games with the other participants. The number of games that the men played between themselves proved to exceed by 66 the number of games that the men played with the women. The number of participants is
(a) 6
(b) 11
(c) 13
(d) None of these
Answer
C
Question. A person always prefers to eat ‘parantha’ and ‘vegetable dish’ in his meal. How many ways can he make his platter in a marriage party, if there are three types of paranthas, four types of ‘vegetable dish’, three types of ‘salads’ and two types of ‘sauces’?
(a) 3360
(b) 4096
(c) 3000
(d) None of these
Answer
A
Question. There are three coplanar parallel lines. If any p points are taken on each of the lines, the maximum number of triangles with vertices on these points is
(a) 3p2 (p -1) + 1
(b) 3p2 (p -1)
(c) p2 (4p -1)
(d) None of these
Answer
C
Question. A lady gives a dinner party for six guests. The number of ways in which they may be selected from among ten friends, if two of the friends will not attend the party together, is
(a) 112
(b) 140
(c) 164
(d) None of these
Answer
B
Question. A person is permitted to select atleast one and atmost n coins from a collection of 2 n + 1 (distinct) coins. If the total number of ways in which he can select coins is 255, then n is equal to
(a) 4
(b) 8
(c) 16
(d) 32
Answer
A
Question. In an steamer, there are stalls for 12 animals and there are horses, cows and calves (not less than 12 each) ready to be shipped in how many ways can the ship load be made?
(a) 312 – 1
(b) 312
(c) (12) 3 – 1
(d) (12)3
Answer
B
Question. How many numbers lying between 10 and 1000 can be formed from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 (repetition of digits is allowed) ?
(a) 1024
(b) 810
(c) 2346
(d) None of these
Answer
B
Question. Let A be a set containing 10 distinct elements. Then, the total number of distinct functions from A to A is
(a) 10!
(b) 1010
(c) 210
(d) 210 -1
Answer
B
Question. In an examination of 9 papers a candidate has to pass in more papers, then the number of papers in which he fails in order to be successful. The number of ways in which he can be unsuccessful, is
(a) 255
(b) 256
(c) 193
(d) 319
Answer
B
Question. Given 5 different green dyes, four different blue dyes and three different red dyes, the number of combinations of dyes which can be chosen taking atleast one green and one blue dye is
(a) 3600
(b) 3720
(c) 3800
(d) 3600
Answer
B
Question. There are four balls of different colours and four boxes of colours same as those of the balls. The number of ways in which the balls, one in each box,could be placed such that a ball does not go to box of its own colour, is
(a) 8
(b) 7
(c) 9
(d) None of these
Answer
C
Question. Five balls of different colours are to be placed in three boxes of different sizes. Each box can hold all five balls. In how many ways can we place the balls so that no box remains empty?
(a) 50
(b) 100
(c) 150
(d) 200
Answer
C
Question. The number of ways of dividing 52 cards amongst four players so that three players have 17 cards each and the fourth players just one card, is
(a) 52/(17|)3
(b) 52!
(c) 52!/17!
(d) None of these
Answer
A
Question. 18 mice were placed in two experimental groups and one control group with all group equally large. In how many ways can the mice be placed into three groups?
(a) 181(6!)2
(b) 181(6!)3
(c) 180(6!)3
(d) None of these
Answer
B
Question. A candidate is required to answer 7 questions out of 12 questions, which are divided into two groups,each containing 6 questions. He is not permitted to attempt more than 5 questions from either group.
Find the number of different ways of doing questions.
(a) 779
(b) 781
(c) 780
(d) 782
Answer
C
Question. In how many ways can `16 be divided into 4 persons when none of them get less than ` 3?
(a) 70
(b) 35
(c) 64
(d) 192
Answer
B
Question. A library has a copies of one book, b copies of each of two books, c copies of each of three books and single copies of d books. The total number of ways in which these books can be distributed, is
(a) (a+b+c+d)! /a!b!c!
(b) (a+b+c+d)! /a!(b!)2(c!)
(c) (a+2b+3c+d)! /a!b!c!
(d) None of these
Answer
B
Question. Eleven books consisting of 5 Mathematics, 4 Physics and 2 Chemistry are placed on a shelf. The number of possible ways of arranging them on the assumption that the books of the same subject are all together, is
(a) 4! 2!
(b) 11!
(c) 5! 4! 3! 2!
(d) None of these
Answer
C
Question. Three boys of class X, four boys of class XI and five boys of class XII sit in a row. The total number of ways in which these boys can sit so that all the boys of same class sit together is equal to
(a) (3!)2 (4!) (5!)
(b) (3!) (4!)2 (5!)
(c) (3!) (4!) (5!)
(d) (3!) (4!) (5!)2
Answer
A
Question. The number of mappings (functions) from the set
A = {1, 2, 3} into the set B = {1, 2, 3, 4, 5, 6,7} such that f (i) £ f ( j), whenever i < j, is
(a) 84
(b) 90
(c) 88
(d) None of these
Answer
A
Question. Let f : {1, 2, 3, 4, 5}® {1, 2, 3, 4, 4, 5} that are onto and f (x) ¹ i is equal to
(a) 9
(b) 44
(c) 16
(d) None of these
Answer
B
Question. The number of triangles that are formed by choosing the vertices from a set of 12 points, seven of which lie on the same line is
(a) 105
(b) 15
(c) 175
(d) 185
Answer
D
Question. The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is
(a) 6
(b) 18
(c) 12
(d) 9
Answer
D
Question. If α = x1 x2 x3 and β = y1 y2 y3 be two three digits numbers, the number of pairs of α and β can be formed so that α can be subtracted fromβ without borrowing is:
a. 2!10!10!
b. 2 (45)(55)
c. 32 .53 .112
d. 136125
Answer
B,C,D
Question. The number of ways of distributing 10 different books among 4 students (S1 − S4 ) such that 1 S and 2 S get 2 books each and 3 S and 4 S get books each is:
a. 12600
b. 25200
c. 10C4
d. 10!/2!2!3!3!
Answer
B,D
Question. The number of ways of arranging seven persons (having A, B, C and D among them) in a row so that A, B, C and D are always in order A–B–C–D (not necessarily together) is:
a. 210
b. 5040
c. 6 × 7C4
d. 7C3
Answer
A,C,D
Question. In a class tournament when the participants were to play one game with another, two class players fell ill, having played 3 games each. If the total number of games played is 84, the number of participants at the beginning was:
a. 15
b. 30
c. 6C2
d. 48
Answer
A,C
Question. Total number of ways of giving at least one coin out of three 25 paise and two 50 pasise coins to a beggar is:
a. 32
b. 12
c. 11
d. 12P1 – 1
Answer
C,D
QuestionThe number of ways to select 2 numbers from {0,1,2,3,4} such that the sum of the squares of the selected numbers is divisible by 5 are: (repetition of digits is allowed)
a. 9C1
b. 9C8
c. 9
d. 7
Answer
A,B,C
Assertion and Reason
Note: Read the Assertion (A) and Reason (R) carefully to mark the correct option out of the options given below:
a. If both assertion and reason are true and the reason is the correct explanation of the assertion.
b. If both assertion and reason are true but reason is not the correct explanation of the assertion.
c. If assertion is true but reason is false.
d. If the assertion and reason both are false.
e. If assertion is false but reason is true.
Question. Assertion: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3
Reason: The number of ways of choosing 3 places from 9 different place is 9C3.
Answer
B
Question. Assertion: If n is a natural number then (n2)!/(n!)n+1 is a natural number.
Reason: The number of ways of dividing mn students into m groups each containing n students is (mn)!/m!(n!)m.
Answer
A
Question. Let n∈ N, and
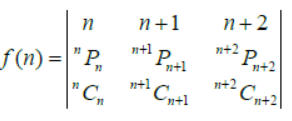
Assertion: f (n) is an integer for all n ∈ N.
Reason: If elements of a determinant are integers, then determinant itself is an integer.
Answer
A
Question.
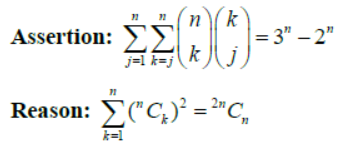
Answer
C
Question. Assertion: The number of ways of distributing at most 12 toys to three children A1, A2 and A3 so that A1 gets at least one, A2 at least three and A3 at most five, is 145.
Reason: the number of non-negative integral solutions.
of x1 + x2 +……..+ x3 ≤ m b is 2. m−1 P2.
Answer
D
Question. Assertion:
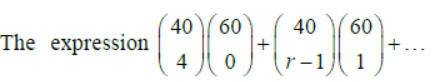
attains maximum value when r = 50.
Reason: (2n r) is maximum when r = n.
Answer
A
Question. Assertion: The number of non-negative integral solution of x1 + x2+…….x20 = 100 is (120 20).
Reason: The number of ways of distributing n identical objects among r persons giving zero or more objects to a person is
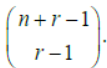
Answer
B
Question.
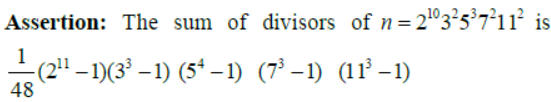
Reason: The number of divisor of m = p1α1 p2α2……..prαr where p1, p2.….pr are distinct primes and α1 , α2….. αr are natural numbers is (α1 +1)(α2 +1)…(αr +1).
Answer
B
Question. Assertion: If p is a prime, the exponent of p in n! is
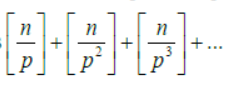
Reason: where [x] denotes the greatest integer ≤ x.
Answer
A
Question. Assertion: A student is allowed to select at most n books from a collection of (2n +1) books. If the total number of ways in which he can select at least one book is 255, then n = 3.
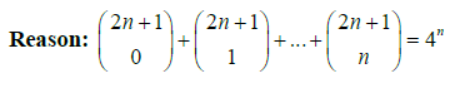
Answer
D

We hope you liked the above provided MCQ Questions Chapter 7 Permutations and Combinations Class 11 Mathematics with solutions. If you have any questions please ask us in the comments box below.


