Please refer to MCQ Questions Chapter 16 Probability Class 11 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 11 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 11 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 16 Probability in Class 11 Mathematics provided below to get more marks in exams.
Chapter 16 Probability MCQ Questions
Please refer to the following Chapter 16 Probability MCQ Questions Class 11 Mathematics with solutions for all important topics in the chapter.
Question. Out of 11 consecutive natural numbers if three numbers are selected at random (without repetition), then the probability that they are in A.P. with positive common difference, is:
(a) 15/101
(b) 5/101
(c) 5/33
(d) 10/99
Answer
C
Question: A five digit number is formed by writing the digits 1, 2, 3, 4, 5, in a random order without repetitions.
Then, the probability that the number is divisible by
4, is
(a) 3/5
(b) 18/5
(c) 1/5
(d) 6/5
Answer
C
Question: The probability of having at least one tail in 4 throws with a coin, is
(a) 15/16
(b) 1/16
(c) 1/4
(d) 1
Answer
A
Question: The number lock of a suitcase has four wheels, each labelled with 10-digits i e. ., from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the right sequence to open the suitcase?
(a) 1/5040
(b) 3/5040
(c) 7/5040
(d) None of these
Answer
A
Question: Four candidates A, B, C, D and have applied for the assignment to coach a school cricket team. If A is twice as likely to be selected as B and B and C are given about the same chance of being selected, while C is twice as likely to be selected as D, what are the probabilities that C will be selected?
(a) 1/9
(b) 2/9
(c) 5/9
(d) 4/9
Answer
B
Question: Three letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the envelopes at random so that each envelope contains exactly one letter. Find the probability that atleast one letter is in its proper envelope.
(a) 1/3
(b) 2/3
(c) 1/5
(d) None of these
Answer
B
Question: Twenty five coins are tossed simultaneously. The probability that the fifth coin will fall with head upwards, is
(a) 5/25
(b) 5/225
(c) 1/2
(d) None of these
Answer
C
Question: If n integers taken at random are multiplied together, then the probability that the last digit of the product is 1,3, 7 or 9 is
(a) 2n/5n
(b) 4n -2n/5n
(c) 4n/5n
(d) None of these
Answer
A
Question: In x=33n ,n is a positive integral value, then what is the probability that x will have 3 at its units place?
(a) 1/3
(b) 1/4
(c) 1/5
(d) 1/2
Answer
B
Question: An insurance salesman sells policies to 5 men, all of identical age and in good health. The probability that a man of this particular age will be alive after 30 yr is 2/3. The probability that after the lapse of 30yr all the five persons will be alive, is
(a) 1/16
(b) 16/81
(c) 32/243
(d) None of these
Answer
C
Question: If odds against solving a question by three students are 2 : 1, 5 : 2 and 5 : 3 respectively, then probability that the question is solved only by one student is
(a) 31/56
(b) 24/56
(c) 25/56
(d) None of these
Answer
C
Question: Two persons A and B take turns in throwing a pair of dice. The first person to through 9 from both dice will be awarded the prize. If A throws first, then the probability that B wins the game, is
(a) 9/17
(b) 8/17
(c) 8/9
(d) 1/9
Answer
B
Question: Two numbers are selected randomly from the set S = {1, 2 ,3, 4, 5 ,6} without replacement one-by-one.
The probability that minimum of the two number is less than 4, is
(a) 1/15
(b) 14/15
(c) 1/5
(d) 4/5
Answer
D
Question: If the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form 7m +7n is divisible by 5, is equal to
(a) 1/4
(b) 1/7
(c) 1/8
(d) 1/49
Answer
A
Question: The accompanying Venn diagram shows three events, A B, and C and also the probabilities of the various intersections [for instance, P (A ∩ B) = 07].
Find P (B ∩ C) and probability of exactly one of the three occurs.
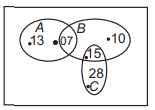
(a) 0.15, 0.15
(b) 0.15, 0.51
(c) 0.15, 0.50
(d) None of these
Answer
B
Question. Let S = {1, 2, ….., 20}. A subset B of S is said to be “nice”, if the sum of the elements of B is 203. Than the probability that a randomly chosen subset of S is “nice” is :
(a) 7/220
(b) 5/220
(c) 1/220
(d) 6/220
Answer
B
Question. Two different families A and B are blessed with equal number of children. There are 3 tickets to be distributed amongst the children of these families so that no child gets more than one ticket.
If the probability that all the tickets go to the children of the family B is 1/12, then the number of children in each family is?
(a) 4
(b) 6
(c) 3
(d) 5
Answer
D
Question. A box ‘A’ contanis 2 white, 3 red and 2 black balls. Another box ¢B¢ contains 4 white, 2 red and 3 black balls. If two balls are drawn at random, without replacement, from a randomly selected box and one ball turns out to be white while the other ball turns out to be red, then the probability that both balls are drawn from box ‘B’ is
(a) 7/16
(b) 9/32
(c) 7/8
(d) 9/16
Answer
A
Question. A set S contains 7 elements. A non-empty subset A of S and an element x of S are chosen at random. Then the probability that xÎA is: [Online April 11, 2014]
(a) 1/2
(b) 64/127
(c) 63/128
(d) 31/128
Answer
B
Question. What is the probability that when one die is thrown,the number appearing on top is even?
(a) 1/6
(b) 1/3
(c) 1/2
(d) None of these
Answer
C
Question. A pair of dice thrown, if 5 appears on atleast one of the dice,thenthe probability that thesumis10 or greater, is
(a) 11/36
(b) 2/9
(c) 3/11
(d) 1/12
Answer
D
Question. There are two balls in an urn. Each ball can be either white or black. If a white ball is put into the urn and there after a ball is drawn at random from the urn, then the probability that it is white is
(a) 1/4
(b) 2/3
(c) 1/5
(d) 1/3
Answer
B
Question. If six students, including two particular students A and B, stand in a row, then the probability that A and B are separated with one student in between them is
(a) 8/15
(b) 4/15
(c) 2/15
(d) 1/15
Answer
B
12. A number n is randomly selected from the set {1, 2, 3, ….. , 1000}. The probability that
(Diagram) is an integer is
(a) 0.331
(b) 0.333
(c) 0.334
(d) 0.332
Answer
C
Question. Four numbers are chosen at random (without replacement) from the set {1, 2, 3, …20}.
Statement -1: The probability that the chosen numbers when arranged in some order will form an AP is 1/85
Statement -2 : If the four chosen numbers form an AP, then the set of all possible values of common difference is (±1,±2,±3,±4,±5) .
(a) Statement -1 is true, Statement -2 is true; Statement -2 is not a correct explanation for Statement -1
(b) Statement -1 is true, Statment -2 is false
(c) Statement -1 is false, Statment -2 is true.
(d) Statement -1 is true, Statement -2 is true ; Statement -2 is a correct explanation for Statement -1.
Answer
B
Question. An urn contains nine balls of which three are red, four are blue and two are green. Three balls are drawn at random without replacement from the urn. The probability that the three balls have different colours is
(a) 2/7
(b) 1/21
(c) 2/23
(d) 1/3
Answer
A
Question. Fifteen coupons are numbered 1 to 15. Seven coupons are selected at random, one at a time with replacement. The probability that the largest number appearing on a selected coupon be 9, is
(a) (1/15)7
(b) (8/18)7
(c) (3/5)7
(d) None of these
Answer
C
Question. A fair coin is tossed repeatedly. If the tail appears on first four tosses, then the probability of the head appearing on the fifth toss is equal to
(a) 1/2
(b) 1/32
(c) 31/32
(d) 1/5
Answer
A
Question. Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is
(a) 2/5
(b) 4/5
(c) 3/5
(d) 15
Answer
A
Question. The probabilities of three events A, B and C are given by P(A) = 0.6, P(B) = 0.4 and P(C) = 0.5. If P (A∪B) = 0.8, P (A∩C) = 0.3, P (A∩B∩C) = 0.2, P (B∩C) = b and P (A∪B∪C) = a, where 0.85 ≤ a ≤ 0.95 , then b lies in the interval:
(a) [0.35, 0.36]
(b) [0.25, 0.35]
(c) [0.20, 0.25]
(d) [0.36, 0.40]
Answer
B
Question. Let A and B be two events such that the probability that exactly one of them occurs is 2/5 and the probability that A or B occurs is 1/2 , then the probability of both of them occur together is:
(a) 0.02
(b) 0.20
(c) 0.01
(d) 0.10
Answer
D
Question. In a class of 60 students, 40 opted for NCC, 30 opted for NSS and 20 opted for both NCC and NSS. If one of these students is selected at random, then the probability that the student selected has opted neither for NCC nor for NSS is :
(a) 1/6
(b) 1/3
(c) 2/3
(d) 5/6
Answer
A
Question. For three events A, B and C,
P(Exactly one of A or B occurs)
= P(Exactly one of B or C occurs)
= P(Exactly one of C or A occurs) = 1/4 and
P(All the three events occur simultaneously) = 1/16.
Then the probability that at least one of the events occurs, is :
(a) 3/16
(b) 7/32
(c) 7/16
(d) 7/64
Answer
C
Question. Without repetition of the numbers, four digit numbers are formed with the numbers 0, 2, 3, 5. The probability of such a number divisible by 5 is
(a) 1/5
(b) 4/5
(c) 1/30
(d) 1/4
Answer
D
Question. From a group of 10 men and 5 women, four member committees are to be formed each of which must contain at least one woman. Then the probability for these committees to have more women than men, is :
(a) 21/220
(b) 3/11
(c) 1/11
(d) 2/23
Answer
C
Question. A die is thrown. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then P(A∪B) is
(a) 3/5
(b) 0
(c) 1
(d) 2/5
Answer
C
Question. Events A, B, C are mutually exclusive events such that P(A) = 3X+1/3 , P(B) = 1-X/4 and P(C)= 1-2X/2 The set of possible values of x are in the interval.
(a) [0 , 1]
(b) [1/3, 1/2]
(c) [1/3, 2/3]
(d) [1/3, 13/3]
Answer
B
Question. A and B are events such that P(A∪B)=3/4, P(A ∩ B)=1/4, P( A ) =2/3 then P ( A ∩ B) is
(a) 5/12
(b) 3/8
(c) 5/8
(d) 1/4
Answer
A
Question. A coin is tossed and a die is thrown. In coin, H and T occur and in die, a number from 1 to 6 may occur. The sample space is
(a) {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
(b) {1H, 2H, 3H, 4H, 5H, 6H, T1, T2, T3, T4, T5, T6}
(c) {H, T, 1, 2, 3, 4, 5, 6}
(d) None of the above
Answer
A
Question. A box contains 1 red and 3 identical white balls. Two balls are drawn at random in succession without replacement. Write the sample space for this experiment.
(a) {RW, WW}
(b) {RW, WW, WR}
(c) {RW, RR}
(d) None of these
Answer
B
Question. The number lock of a suitcase has four wheels, each labelled with 10-digits i. e., from0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the right sequence to open the suitcase?
(a) 1/5040
(b) 3/5040
(c) 7/ 5040
(d) None of these
Answer
A
Question. Four candidates A, B, Cand D have applied for the assignment to coach a school cricket team. If A is twice as likely to be selected as B and B and C are given about the same chance of being selected, while C is twice as likely to be selected as D, what are the probabilities that C will be selected?
(a) 1/9
(b) 2/9
(c) 5/9
(d) 4/9
Answer
B
3. Which of the following cannot be valid assignments of probabilities for outcomes of sample space
S = {W1 ,W2 ,W3 ,W4 ,W5 ,W6 ,W7 } ?
(Diagram)
(a) I, II
(b) I, III
(c) II, III, IV
(d) None of these
Answer
D
Question. A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of the numbers that turn up is 3.
(a) – 1/12
(b) 1/12
(c) 1/3
(d) 1/4
Answer
B
Question. In x = 33n , nis a positive integral value, then what is the probability that x will have 3 at its units place?
(a) 1/3
(b) 1/4
(c) 1/5
(d) 1/2
Answer
B
Question. Two persons A and Btake turns in throwing a pair of dice. The first person to through 9 from both dice will be awarded the prize. If A throws first, then the probability that B wins the game, is
(a) 9/17
(b) 8/17
(c) 8/9
(d) 1/9
Answer
B
Question. Three of the six vertices of a regular hexagon are chosen at random. The probability that the triangle with these three vertices is equilateral is equal to
(a) 1/2
(b) 1/5
(c) 1/10
(d) 1/20
Answer
C
Question. In a large metropolitan area, the probabilities are 0.87, 0.36, 0.30 that a family (randomly chosen for a sample survey) owns a colour television set, a black and white television set or both kinds of sets. What is the probability that a family owns either anyone or both kinds of sets?
(a) 0.95
(b) 0.93
(c) 0.98
(d) None of these
Answer
B
Question. While shuffling a pack of 52 playing cards, 2 are accidentally dropped. Find the probability that the missing cards to be of different colours.
(a) 29/52
(b) 1/2
(c) 26/51
(d) 27/51
Answer
C
Question. Seven persons are to be seated in a row. The probability that two particular persons sit next to each other is
(a) 1/3
(b) 1/6
(c) 2/7
(d) 1/2
Answer
C
Question. A card is drawn from a deck of 52 cards. Find the probability of getting a king or a heart or a red card.
(a) 5/13
(b) 7/13
(c) 25/52
(d) None of these
Answer
B
Question. If from each of three boxes containing 3 white and 1 black, 2 white and 2 black, 1 white and 3 black balls, one ball is drawn at random, then the probability that 2 white and 1 black ball will be drawn, is
(a) 13/32
(b) 1/4
(c) 1/32
(d) 3/16
Answer
A
Question. There are four machines and it is known that exactly two of them are faulty. They are tested, one-by-one in a random order till both the faulty machines are identified. Then, the probability that only two tests are needed, is
(a) 1/3
(b) 1/6
(c) 1/2
(d) 1/4
Answer
B
Question. If the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form7m + 7n is divisible by 5, is equal to
(a) 1/4
(b) 1/7
(c) 1/8
(d) 1/49
Answer
A
Question. If n integers taken at random are multiplied together, then the probability that the last digit of the product is 1,3, 7 or 9 is
(a) 2n / 5n
(b) 4n – 2n / 5n
(c) 4n / 5n
(d) None of these
Answer
A
Question. There are 9999 tickets bearing numbers 0001, 0002, … , 9999. If one ticket is selected from these tickets at random, the probability that the number on the ticket will consists of all different digits, is
(a) 5040/9999
(b) 5000/9999
(c) 5030/9999
(d) None of these
Answer
A
Question. An unbiased die with faces marked 1, 2, 3, 4, 5 and 6 is rolled four times. Out of four face values obtained,the probability that the minimum face value is not less than 2 and the maximum face value is not greater than 5, is
(a) 16/81
(b) 1/81
(c) 80/81
(d) 65/81
Answer
A
Question. The probabilities of winning a race by three persons A, B and C are 1/2, 1/4 and 1/4, respectively. They run two races. The probability of A winning the second race when B wins the first race is
(a) 1/3
(b) 1/2
(c) 1/4
(d) 2/3
Answer
B
Question. A letter is taken out at random from ‘ASSISTANT’ and another is taken out from ‘STATISTICS’. The probability that they are the same letters is
(a) 1/45
(b) 13/90
(c) 19/90
(d) None of these
Answer
C
Question. If A and Bare any two events, then P(A̅ ∩ B) is equal to
(a) P(A̅) P(B̅)
(b) 1 – P(A) – P(B)
(c) P(A) + P(B) – P(A ∩ B)
(d) P(B) – P(A ∩ B)
Answer
D
Question. If E and F are events such that P(E) = 1 /4 , P(F) = 1/2 and P(Eand F) = × 1/8 Find (i) P(E or F) (ii) P (not E and not F).
(a) 1/8 ,7/8
(b) 5/8 ,3/8
(c) 1/7 ,6/7
(d) None of these
Answer
B
Question. A bag contains 5 white and 3 black balls and 4 balls are successively drawn out and not replaced. Theprobability that they are alternately of different colours, is
(a) 1/196
(b) 2/7
(c) 13/56
(d) 1/7
Answer
D
Question. Three numbers are chosen from 1 to 20. Find the probability that they are not consecutive.
(a) 186/190
(b) 187/190
(c) 188/190
(d) 18/20C3
Answer
B
Question. A single letter is selected at random from the word ‘PROBABILITY’. The probability that it is a vowel is
(a) 1/3
(b) 4/11
(c) 2/11
(d) 3/11
Answer
A

We hope you liked the above provided MCQ Questions Chapter 16 Probability Class 11 Mathematics with solutions. If you have any questions please ask us in the comments box below.


