Please refer to MCQ Questions Chapter 12 Linear Programming Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 12 Linear Programming in Class 12 Mathematics provided below to get more marks in exams.
Chapter 12 Linear Programming MCQ Questions
Question. Objective function of a L.P.P is
(a) A quadratic function
(b) A constraint
(c) A linear function to optimized
(d) None of these
Answer
C
Question. The function f (x)= a cos x+ b tan x+x has extreme values at x = 0 and x =π/6, then
(a) a = – 2/3,b=-1
(b) a=2/3, b=-1
(c) a = -2/3,b=1
(d) a =2/3, b=1
Answer
A
Question. The maximum value of f (x)= x/4+x+x2 on [-1,1] is
(a) -1/4
(b) -1/3
(c) 1/6
(d) 1/5
Answer
C
Question. The absolute maximum and minimum values of the function f given by f(x)= cos2 x +sin x, x∈[0,π]
(a) 2.25 and 2
(b) 1.25 and 1
(c) 1.75 and 1.5
(d) None of these
Answer
B
Question. In interval [1,e], the greatest value of x2 log is
(a) e2
(b) 1/e log 1/√e
(c) e2 log √e
(d) None of these
Answer
A
Question. The point of inflexion for the curve y =x 5/2 is
(a) (1, 1)
(b) (0, 0)
(c) (1, 0)
(d) (0, 1)
Answer
B
Question. The function f (x)= |px-q|+r|x|, x∈(-∞,∞), where p<0, q >0,r>0
(a) p≠ q
(b) r≠ q
(c) r ≠p
(d) p= q= r
Answer
C
Question. The two positive numbers x and y such that their sum is 35 and the product is x y2 5 is maximum, are
(a) 15 and 20
(b) 10 and 25
(c) 5 and 30
(d) None of these
Answer
B
Question. A square piece of tin of side 18 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps of the box. What should be the side of the square to be cut-off so that the volume of the box is maximum possible?
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 9 cm
Answer
A
Question. The two positive numbers whose sum is 16 and the sum of whose cubes is minimum, are
(a) 4 and 12
(b) 6 and 10
(c) 8 and 8
(d) None of these
Answer
C
Question. The right circular cone of least curved surface area and given volume has an altitude equal to
(a) two times the radius of the base.
(b) √3 times the radius of the base.
(c) √2 times the radius of the base.
(d) None of the above
Answer
C
Question. The closed right circular cylinder of given surface and maximum volume is such that its height is equal to
(a) the radius of the base
(b) the diameter of the base
(c) the twice of diameter of the base
(d) None of the above
Answer
B
Question. The semi-vertical angle of the cone of the maximum volume and of given slant height is
(a) tan-1√3
(b) tan-1√2
(c) tan-1(1/√2)
(d) None of the above
Answer
B
Question. The point on the curve x2=2y which is nearest to the point (0,5) is
(a) ( 2√2,4)
(b) (2√2,0)
(c) (0, 0)
(d) (2,2)
Answer
A
Question. The semi-vertical angle of right circular cone of given surface area and maximum volume is
sin– 1(1/3)·
(a) sin-1(1/3)
(b) sin-1(1/2)
(c) sin-1(√3)
(d) None of these
Answer
A
Question. The maximum area of an isosceles triangle inscribed in the ellipse x2/a2 + y2/b2= 1 with its vertex at one end of the major axis.
(a) 3/4ab sq unit
(b) 3/4 √3 ab sq unit
(c) √3/4 ab sq unit
(d) None of these
Answer
B
Question. A window is in the form of a rectangle surmounted by a semi-circle opening. The perimeter of the window is 10 m. The dimensions of the window to admit maximum light through the whole opening is
(a) length = breadth =1/π+4
(b) length = 20/π+4 and breadth =10/π+4
(c) length = 2/π+4 and breadth =1/π+4
(d) None of the above
Answer
B
Question. The sum of the perimeter of a circle and square is k, where k is some constant, then the sum of their areas is least when the side of square is
(a) equal to the radius of the circle
(b) double the radius of the circle
(c) triple the radius of the circle
(d) None of the above
Answer
B
Question. The altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is
(a) r/2
(b) r/3
(c) 3r/4
(d) 4r/3
Answer
D
Question. The height of the cylinder of maximum volume that can be inscribed in a sphere of radius R and the maximum volume respectively

Answer
A
Question. If the sum of the length of the hypotenuse and a side of a right angled triangle is given. Then, the area of the triangle is maximum when the angle between them is
(a) π/6
(b) π/4
(c) π/3
(d) π/2
Answer
C
Question. The height of the cylinder of greatest volume which can be inscribed in a circular cone of height h and having semi-vertical angle a and the greatest volume of cylinder are respectively
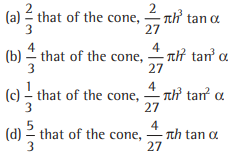
Answer
C
Question. Maximum slope of the curve y =-x3+3×2+9x-27 is
(a) 0
(b) 12
(c) 16
(d) 32
Answer
B
Question. If P,Q and P, R are the two sides of a triangle, then the angle between them which gives maximum area of the triangle, is
(a) π
(b) π / 3
(c) π / 4
(d) π / 2
Answer
D
Question. If ab = 2a+3b,a>0,b>0,then the minimum value of ab is
(a) 12
(b) 24
(c) 1/4
(d) None of these
Answer
B
Question. The minimum radius vector of the curve a2/x2+ b2/y2=1 is of length
(a) a- b
(b) a+ b
(c) 2a +b
(d) None of these
Answer
B
Question. if a2x4+b2y4=c6, then maximum value of xy is
(a) c2/√ab
(b)c3/ab
(c) c3/√2ab
(d) c3/2ab
Answer
C
Question. The perimeter of a sector is p. The area of the sector is maximum, when its radius is
(a) √p
(b) 1/√p
(c) p/2
(d) p/4
Answer
D
Question. If xy= c2 , then minimum value of xy is
(a) c√ab
(b)2c√ab
(c) -c√ab
(d) -2c√ab
Answer
B
Question. A cone of maximum volume is inscribed in the given sphere, then ratio of the height of the cone to diameter of the sphere is
(a) 2/3
(b) 3/4
(c) 1/3
(d) 1/4
Answer
A
Question. The tangent to the curve y =x3-6x2+9x+4,0≤x≤5 has maximum slope at x which is equal
(a) 2ion.
(b) 3
(c) 4
(d) None of these
Answer
D
Question. A given right circular cone has volume p and the largest right circular cylinder that can be inscribed in the cone has a volume q. Then, p q: is
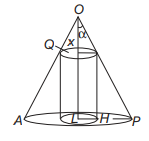
(a) 9 :
(b) 8 : 3
(c) 7 : 2
(d) None of these
Answer
A
Question. The set of all values of the parameter a for which the points of minimum of the function y=1+a2x-x3 satisfy the inequality x2+x+2/x2+5x+6 ≥0,is
(a) an empty set
(b) (-3√3,-2√3)
(c) (2√3,3√3)
(d) (-3√3,-2√3)∪ (2√3,3√3)
Answer
C
Question. The optimal value of the objective function is attained at the points
(a) Given by the intersection of inequations with x-axis only
(b) Given by the corner points of the feasible region
(c) Given by the intersection of inequations with the axes only
(d) None of these
Answer
B
Question. The solution set of the inequation 3𝑥 + 5𝑦 < 4 is
(a) Open half plane not containing the origin.
(b) When xy-plane except the points lying on the line 3𝑥 + 5𝑦 = 4
(c) Open half plane containing origin.
(d) None of these.
Answer
C
Question. The solution set of the inequation 𝑥 + 3𝑦 ≥ 6 is
(a) Half plane not containing the origin.
(b) Whole xy-plane except the points lying on the line 𝑥 + 3𝑦 = 6
(c) Open half plane containing the origin.
(d) None of these.
Answer
A
Question. Of all of the points of the feasible region for maximum or minimum of objective function the points
(a) Inside the feasible region
(b) At the boundary line of the feasible region
(c) Vertex point of the boundary of the feasible region
(d) None of these
Answer
C
Question. A set of values of decision variables which satisfies the linear constraints and non-negativity conditions of L.P.P is called its
(a) Unbounded solution
(b) Optimum solution
(c) Feasible solution
(d) None of these
Answer
C
Question. Shaded region in the following figure is represented by
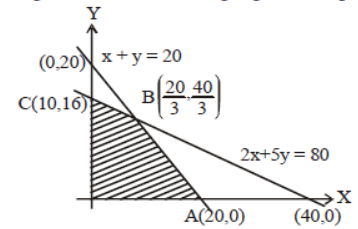
(a) 2x + 5y ≥ 80, x + y ≤ 20, x ≥ 0, y ≤ 0
(b) 2x + 5y ≥ 80, x + y ≥ 20, x ≥ 0, y ≥ 0
(c) 2x + 5y ≤ 80, x + y ≤ 20, x ≥ 0, y ≥ 0
(d) 2x + 5y ≤ 80, x + y ≤ 20, x ≤ 0, y ≤ 0
Answer
C
Question. Consider Max. z = – 2x – 3y subject to x/2 + y/3 ≤ 1 , x/3 + y/2 ≤ 1, x, y ≥ 0The max value of z is :
(a) 0
(b) 4
(c) 9
(d) 6
Answer
A
Question. The solution region satisfied by the inequalities x + y ≤ 5, x ≤ 4, y ≤ 4, x ≥ 0, y ≥ 0,5x + y ≥ 5, x + 6y ≥ 6, is bounded by
(a) 4 straight lines
(b) 5 straight lines
(c) 6 straight lines
(d) unbounded
Answer
B
Question. Which of the following statement is correct?
(a) Every L.P.P. admits an optimal solution
(b) A L.P.P. admits a unique optimal solution
(c) If a L.P.P. admits two optimal solutions, it has an infinite number of optimal solutions
(d) The set of all feasible solutions of a L.P.P. is not a convex set.
Answer
C
Question. The graph of inequations x ≤ y and y ≤ x + 3 is located in
(a) II quadrant
(b) I, II quadrants
(c) I, II, III quadrants
(d) II, III, IV quadrants
Answer
C
Question. Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0) . Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
(a) p = 2 q
(b) p = q/2
(c) p = 3 q
(d) p = q
Answer
B
Question. L.P.P. has constraints of
(a) one variables
(b) two variables
(c) one or two variables
(d) two or more variables
Answer
D
Question. The value of objective function is maximum under linear constraints, is
(a) At the centre of feasible region
(b) At (0, 0)
(c) At any vertex of feasible region
(d) The vertex which is at maximum distance from (0, 0)
Answer
C
Question. The feasible region for LPP is shown shaded in the figure.
Let f = 3 x – 4 y be the objective function, then maximum value of f is

(a) 12
(b) 8
(c) 0
(d) –18
Answer
C
Question. The point at which the maximum value of ( 3x + 2y) subject to the constraints x + y ≤ 2, x ≥ 0, y ≥ 0 is obtained, is
(a) (0, 0)
(b) (1.5, 1.5)
(c) (2, 0)
(d) (0, 2)
Answer
C
Question. Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (3, 0)
(b) (1/2 , 5/2)
(c) (7, 0)
(d) (0, 5)
Answer
D
Question. Which of the following is not a vertex of the positive region bounded by the inequalities 2x + 3y ≤ 6, 5x + 3y ≤ 15 and x, y ≥ 0 ?
(a) (0, 2)
(b) (0, 0)
(c) (3, 0)
(d) None
Answer
D
Question. A brick manufacture has two depots A and B, with stocks of 30000 and 20000 bricks respectively. He receive orders from three builders P, Q and R for 15000, 20,000 and 15000 bricks respectively. The cost (in `) of transporting 1000 bricks to the builders from the depots as given in the table.

The manufacturer wishes to find how to fulfill the order so that transportation cost is minimum. Formulation of the L.P.P., is given as
(a) Minimize Z = 40x – 20y Subject to, x + y ≥ 15, x + y ≤ 30, x ≥ 15, y ≤ 20, x ≥ 0, y ≥ 0
(b) Minimize Z = 40x – 20y Subject to, x + y ≥ 15, x + y ≤ 30, x ≤ 15, y ≥ 20, x ≥ 0, y ≥ 0
(c) Minimize Z = 40x – 20y Subject to, x + y ≤ 15, x + y ≤ 30, x ≤ 15, y ≤ 20, x ≥ 0, y ≥ 0
(d) Minimize Z = 40x – 20y Subject to, x + y ≥ 15, x + y ≤ 30, x ≥ 15, y ≥ 20, x ≥ 0, y ≥ 0
Answer
C
Question. The area of the feasible region for the following constraints 3y + x ≥3, x ≥ 0, y ≥ 0 will be
(a) Bounded
(b) Unbounded
(c) Convex
(d) Concave
Answer
B
Question. Consider the objective function Z = 40x + 50y. The minimum number of constraints that are required to maximize Z are
(a) 4
(b) 2
(c) 3
(d) 1
Answer
C
Question. The region represented by the inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 10, x ≥ 0, y ≥ 0 is
(a) unbounded
(b) a polygon
(c) exterior of a triangle
(d) None of these
Answer
D
Question. Maximize 𝑍 = 11𝑥 + 8𝑦 𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 𝑥 ≤ 4, 𝑦 ≤ 6, 𝑥 + 𝑦 ≤ 6, 𝑥, 𝑦 ≥ 0
(a) 44 at (4,2)
(b) 60 at (4,2)
(c) 62 at (4,0)
(d) 48 at (4,2)
Answer
B
Question. Maximize 𝑍 = 4𝑥 + 6𝑦, 𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 3𝑥 + 2𝑦 ≤ 12, 𝑥 + 𝑦 ≥ 4, 𝑥, 𝑦 ≥ 0
(a) 16 at (4,0)
(b) 24 at (0,4)
(c) 24 at (6,0)
(d) 36 at (0,6)
Answer
D
Question. If the objective function for an L.P.P. Z= 3x-4y and the corner points for the bounded feasible region are (0,0)(5,0)(6,5)(6,8), (4,10)𝑎𝑛𝑑(0,8) then the minimum value of Z occurs at
(a) (0,0)
(b) (0,8)
(c) (5,0)
(d) (4,10)
Answer
B
Question. Refer to Q.9 above , the maximum Z occurs at
(a) (5,0)
(b) (6,5)
(c) (6,8)
(d) (4,10)
Answer
A
Question. Objective function of L.P.P is
(a) a constraint
(b) a function to be optimized
(c) a relation between variables
(d) none
Answer
B
Question. The feasible region always for an L.L.P is always
(a) convex
(b) concave
(c) may be convex or concave
(d) none
Answer
A
Question. In a L.P.P, if the objective function Z = ax +by has same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ……………. Value.
(a) minimum
(b) maximum
(c) may or may not maximum
(d) none
Answer
B
Question. The corner points of the feasible region for an L.P.P. are (0,3), (1,1), and (3,0). If objective function is 𝑍 = 𝑝𝑥 + 𝑞𝑦, 𝑝, 𝑞 >0, then the condition on p and q so that the minimum of Z occurs at (3,0) and (1,1) is
(a) p=2q
(b) p=q/2
(c) p=3q
(d) p=q
Answer
B
Question. If the corner points of the feasible region for an L.P.P. are (0,2), (3,0) ,(6,0), (6,8) and (0,5), then minimum value of the objective function F = 4X+6Y occurs at
(a) (0,2) only
(b) (3,0) only
(c) the mid point of the line segment joining the points (0,2) and(3,0) only
(d) every point on the line segment joining the points (0,2) and (3,0)
Answer
D
Question. The point at which the maximum value of x + y , subject to the constraints 𝑥 + 2𝑦 ≤ 70, 2𝑥 + 𝑦 ≤ 95, 𝑥, 𝑦, ≥ 0 is obtained , is
(a) (30,25)
(b) (20,35)
(c) (35,20)
(d) (40,15)
Answer
D
Question. Which of the following statement is correct ?
(a) Every L.P.P admits an optimal solution
(b) A LPP admits unique optimal solution
(c) if a LPP admits two optimal solutions it has an infinite number of optimal solutions
(d) the set of all feasible solutions of a LPP is not a converse set
Answer
C
Question. If the constraints in a linear programming problem are changed
(a) The problem is to be re-evaluated
(b) Solution is not defined
(c) The objective function has to be modified
(d) the change in constraints is ignored.
Answer
A
Question. The maximum value of 𝑍 = 4𝑥 + 2𝑦 subjected to the constraints 2𝑥 + 3𝑦 ≤ 18, 𝑥 + 𝑦 ≥ 10; 𝑥, 𝑦 ≥ 0 𝑖𝑠
(a) 36
(b) 40
(c) 20
(d) None of these
Answer
D
Question. The objective function 𝑍 = 4𝑥 + 3𝑦 𝑐𝑎𝑛 𝑏𝑒 𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑒𝑑 𝑠𝑢𝑏𝑗𝑒𝑐𝑡𝑒𝑑 𝑡𝑜 𝑡ℎ𝑒 𝑐𝑜𝑛𝑠𝑡𝑟𝑎𝑖𝑛𝑡𝑠 3𝑥 + 4𝑦 ≤ 24, 8𝑥 + 6𝑦 ≤ 48, 𝑥 ≤ 5, 𝑦 ≤ 6; 𝑥, 𝑦 ≥ 0
(a) At only one point
(b) At two points only
(c) At an infinite number of points
(d) None of these
Answer
C
Assertion – Reason Type Questions :
(a) Assertion is correct, Reason is correct; Reason is a correct explanation for assertion.
(b) Assertion is correct, Reason is correct; Reason is not a correct explanation for Assertion
(c) Assertion is correct, Reason is incorrect
(d) Assertion is incorrect, Reason is correct.
Question. Assertion : The region represented by the set {(x, y) : 4 ≤ x2 + y2 ≤ 9} is a convex set.
Reason : The set {(x, y) : 4 ≤ x2 + y2 ≤ 9} represents the region between two concentric circles of radii 2 and 3.
Answer
D
Question. Assertion : If a L.P.P. admits two optimal solutions then it has infinitely many optimal solutions.
Reason : If the value of the objective function of a LPP is same at two corners then it is same at every point on the line joining two corner points.
Answer
A
We hope you liked the above provided MCQ Questions Chapter 12 Linear Programming Class 12 Mathematics with solutions. If you have any questions please ask us in the comments box below.


