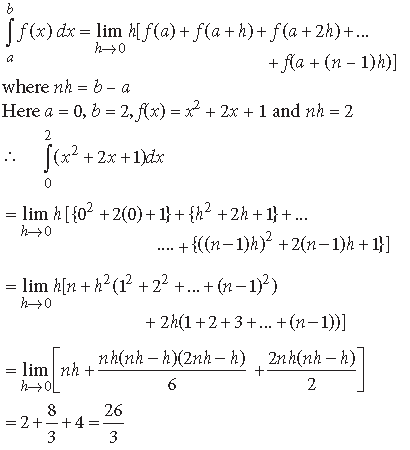Integrals Class 12 Mathematics Important Questions

Please refer to Integrals Class 12 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.

Class 12 Mathematics Important Questions Integrals

Very Short Answer Type Questions

Question.

Answer.

Question.

Answer.

Question. Write the value of ∫sec x(sec x + tan x)dx
Answer. ∫sec x (sec x + tan x)dx
=∫(sec² x + sec x tan x)dx = tan x + sec x + C

Question.

Answer.

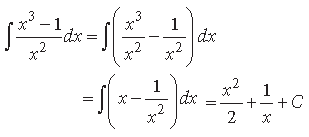
Question. Write the value of ∫2^x dx
Answer.

Question.

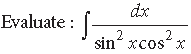
Answer.

Question.

Answer.

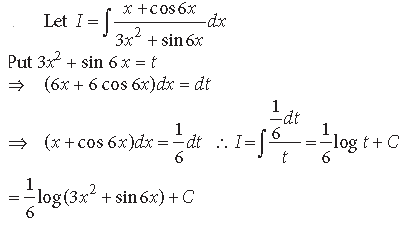
Question.

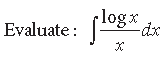
Answer.

Question.

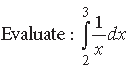
Answer.

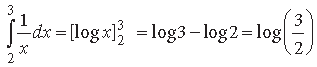
Question.

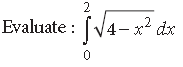
Answer.

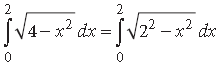
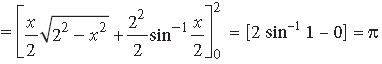
Question.

Answer.

Question. Evaluate : ∫x log 2x dx.
Answer.

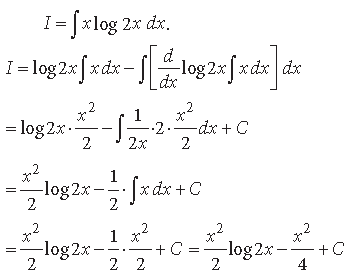
Question.

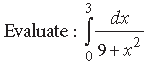
Answer.

∴ By second fundamental theorem of integral calculus, we have

Question. Given ∫e^x (tan x +1)secx dx = e^x f (x) + c Write f(x) satisfying above.
Answer. Given : ∫e^x (tanx +1)secx dx = e^x f(x) + C …(1)
L.H.S. = ∫e^x (tanx +1)secx dx
= ∫e^x (secx + secx tanx)dx
= ∫e^x secx dx + ∫e^x secx tanx dx
(Integrating first integral by parts)
= e^x secx −∫e^x sec x tan x dx +∫e^x secx tanx dx +C
= e^x sec x + C = e^x f(x) + C (by (1))
On comparing, we get f(x) = sec x

Question.

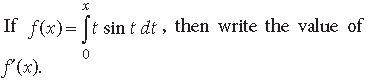
Answer. By the first fundamental theorem of integral calculus

Question.

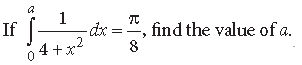
Answer.

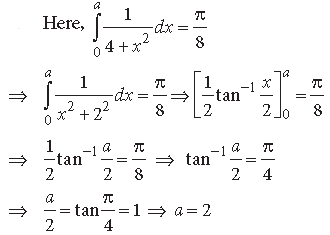
Question.

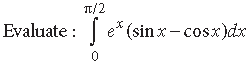
Answer.

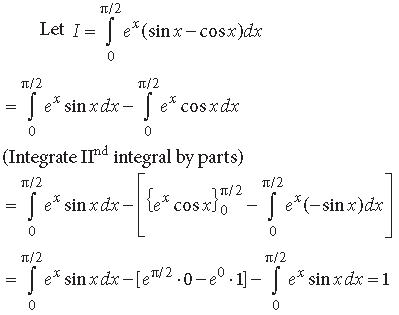
Question. Evaluate : ∫sec²(7 − 4x)dx
Answer. Let I = ∫sec²(7 − 4x)dx

Question. Evaluate : ∫cos4x cos³xdx
Answer. Let I = ∫cos4x cos3xdx

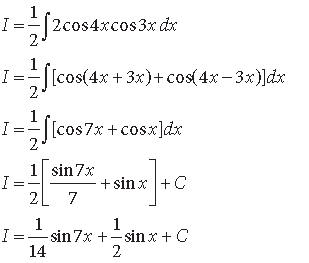
Question.

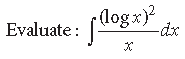
Answer.

Short Answer Type Questions

Question.

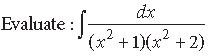
Answer.

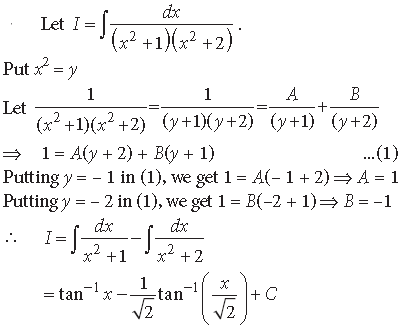
Question.

Answer.

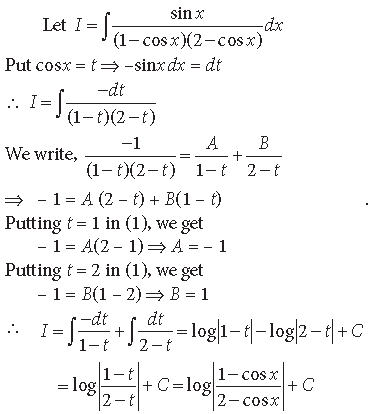
Question.

Answer.

Question.

Answer.

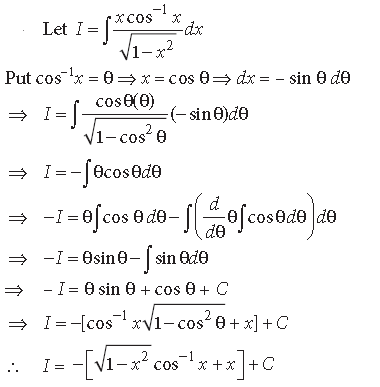
Question.

Answer.

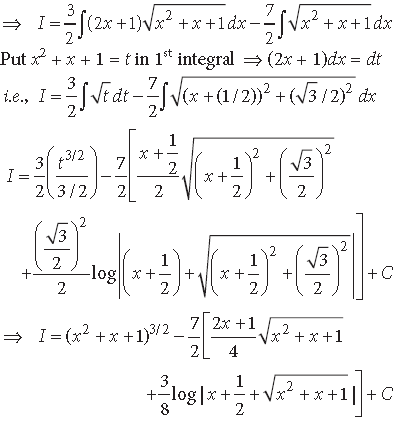
Question.

Answer.

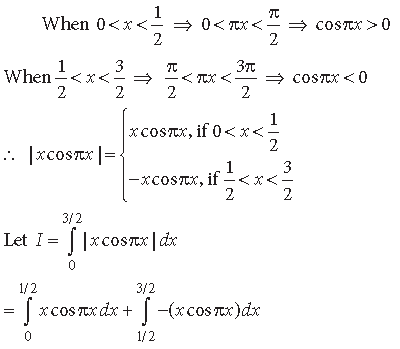
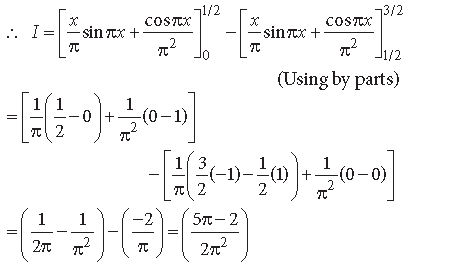
Question.

Answer.

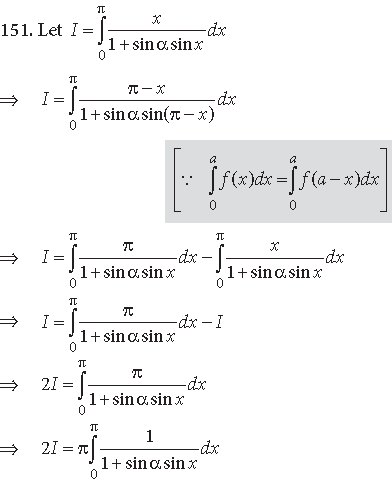
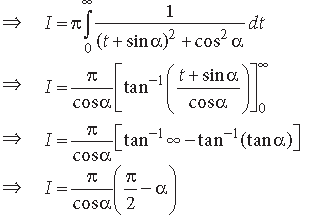
Question.

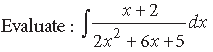
Answer.

Question.

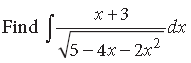
Answer.

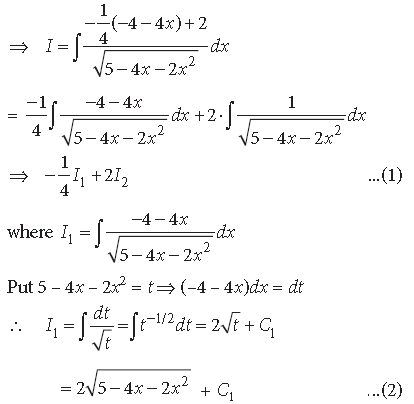
Question.

Answer.

Question.

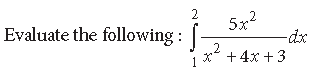
Answer.

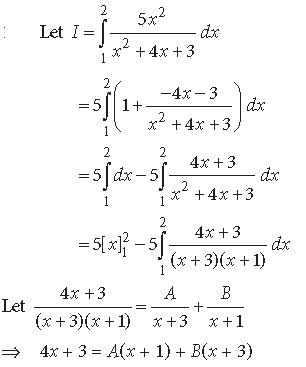
Question.

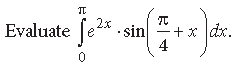
Answer.

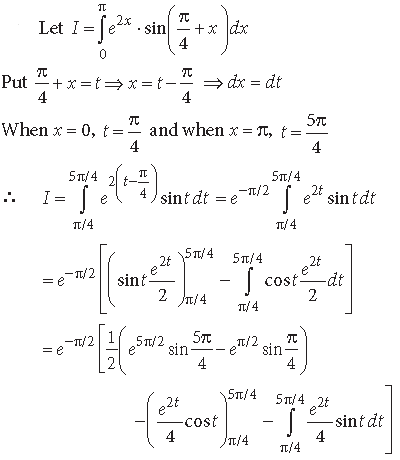
Question.

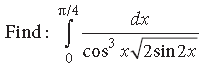
Answer.

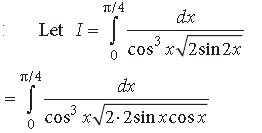
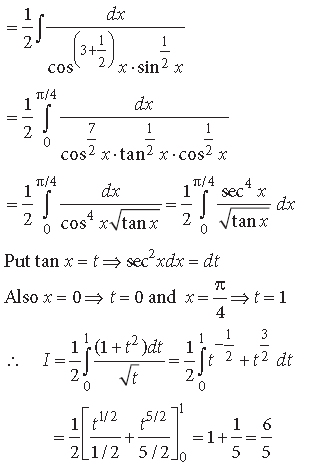
Question.

Answer.

Question.

Answer.

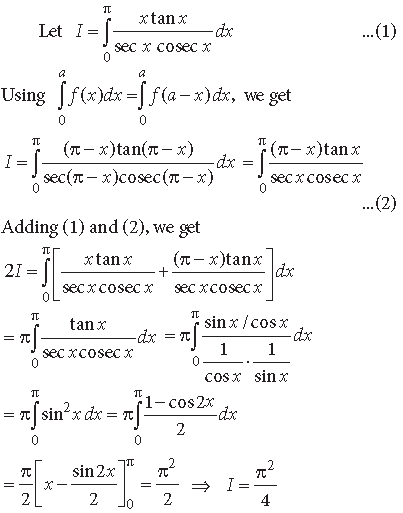
Question.

Answer.

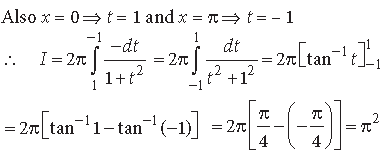
Question.

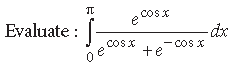
Answer.

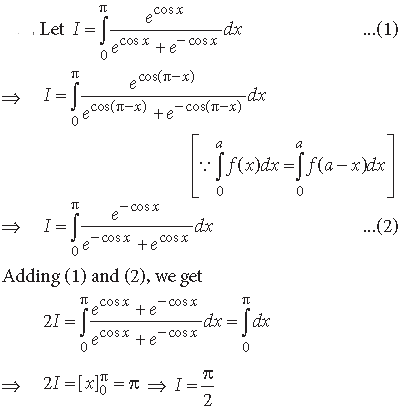
Question.

Answer.

Question.

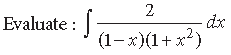
Answer.

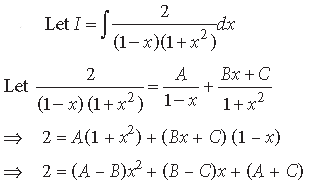
Question.

Answer.

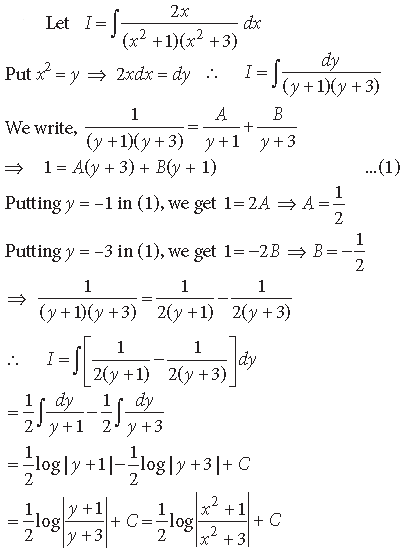
Question.

Answer.

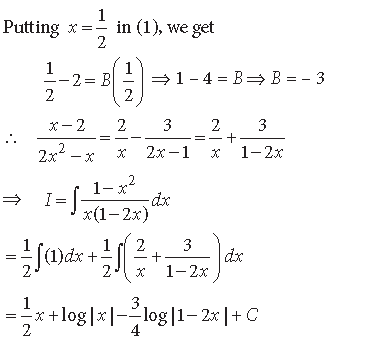
Question.

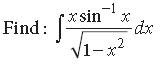
Answer.

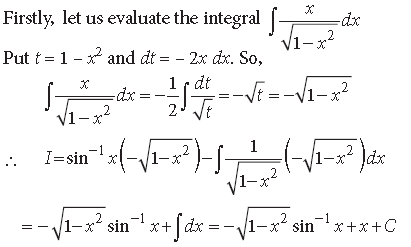
Question.

Answer.

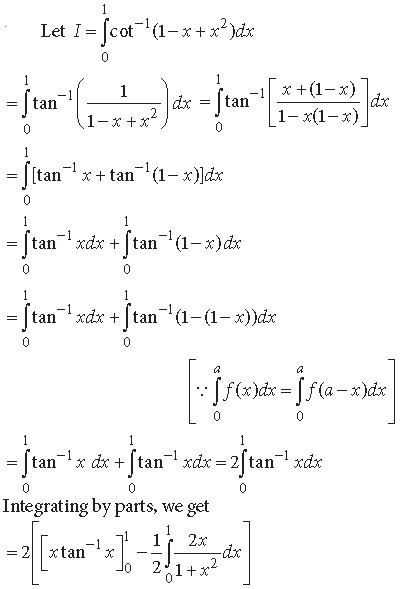
Question.

Answer.

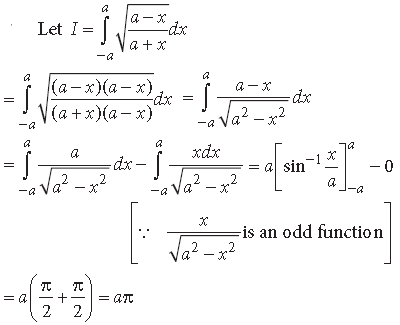
Question.

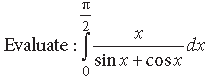
Answer.

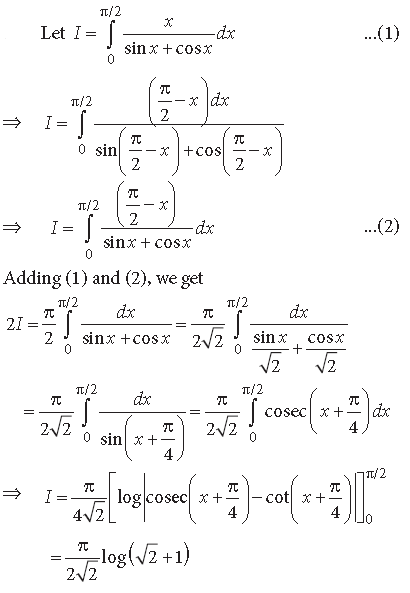
Question. Evaluate : ∫(| x | + | x − 2 | + | x − 4 |)dx
Answer. Let I = ∫(| x | + | x − 2 | + | x − 4 |)dx

Question. Evaluate : ∫[| x − 2 | + | x − 3| + | x − 5|]dx

Answer.

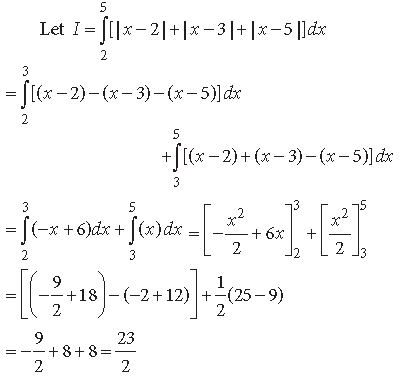
Question. Evaluate : ∫[| x −1| + | x − 2 | + | x − 3|]dx

Answer.

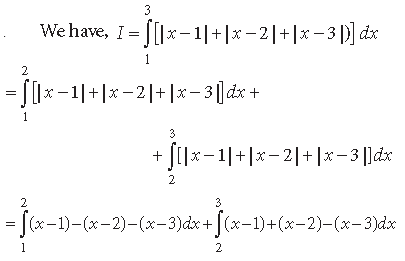
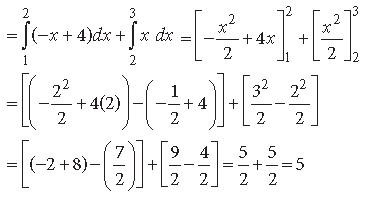
Question.

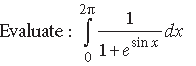
Answer.

Question.

Answer.

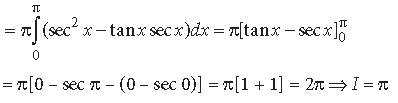
Question.

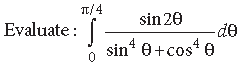
Answer.

Question.

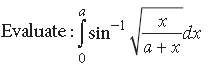
Answer.

Integrating by parts, taking (tan t sec² t) as 2^nd function.

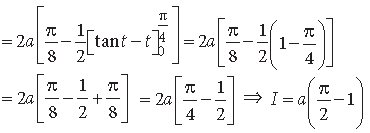
Question.

Answer.

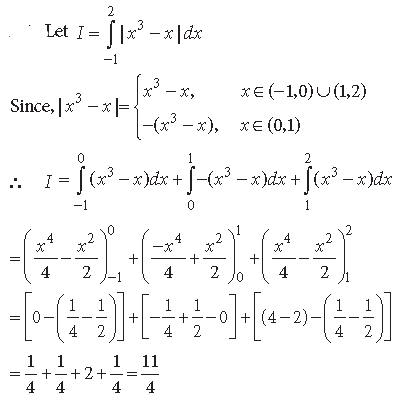
Question.

Answer.

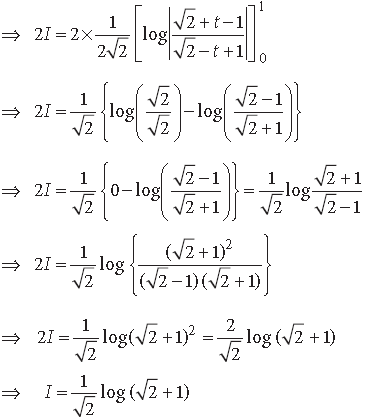
Question.

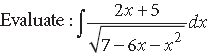
Answer.

Question.

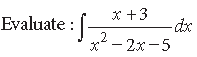
Answer.

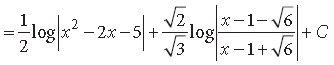
Question.

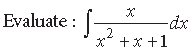
Answer.

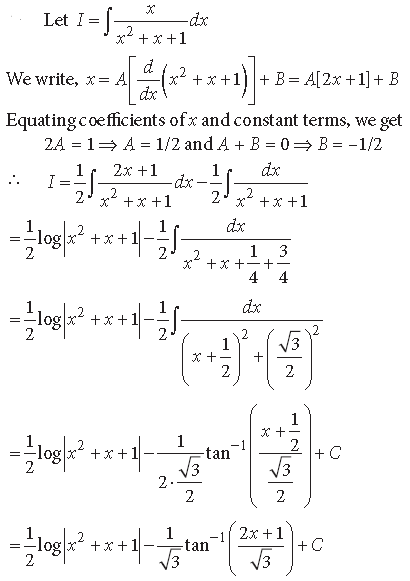
Question.

Answer.

Question.

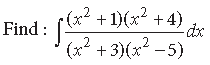
Answer.

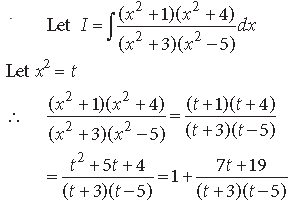
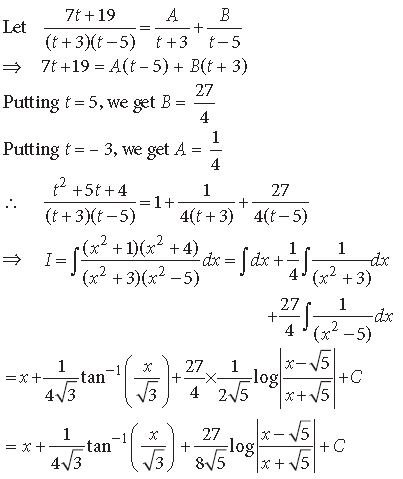
Question.

Answer.

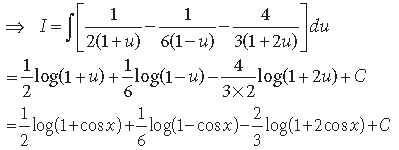
Question.

Answer.

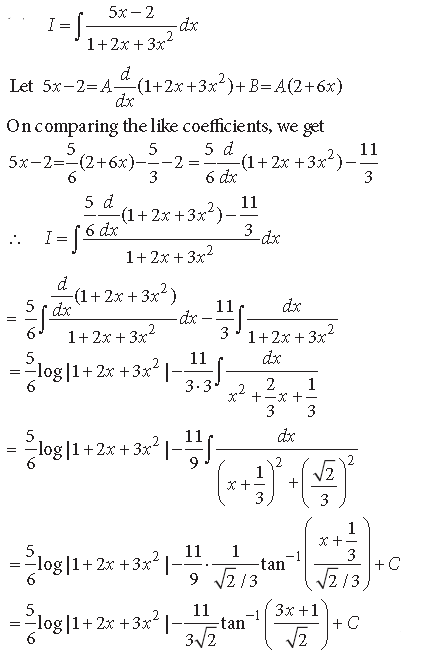
Question.

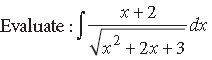
Answer.

Question.

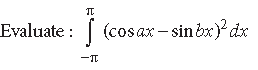
Answer.

Question.

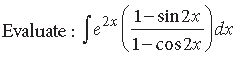
Answer.

Question.

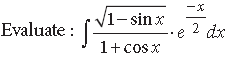
Answer.

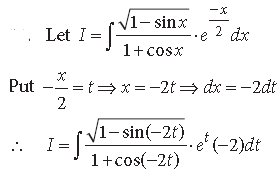
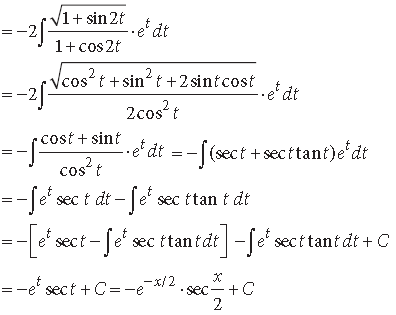
Question.

Answer.

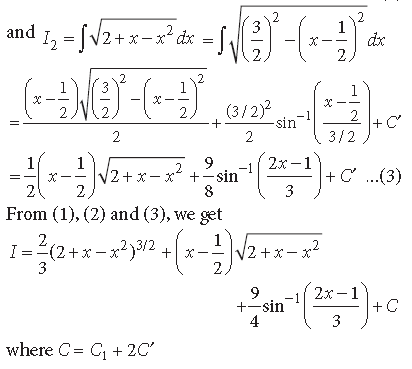
Question.

Answer.

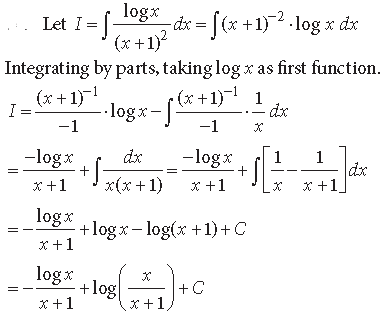
Question. Evaluate : ∫e^2x – sin(3x +1)dx

Answer.

Question.

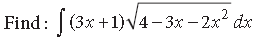
Answer.

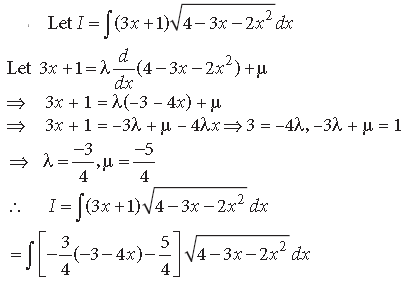
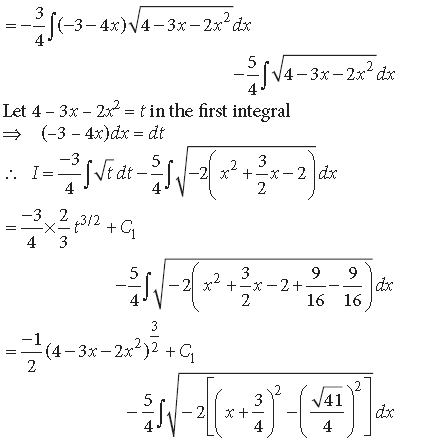
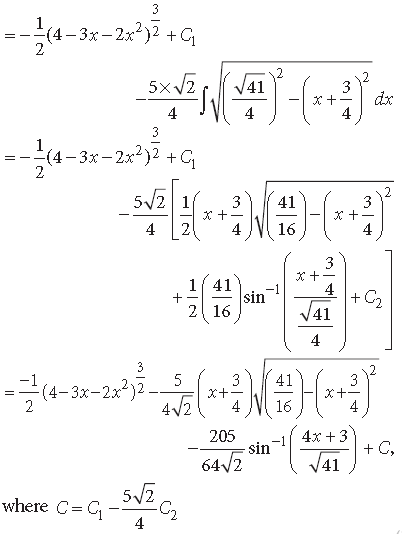
Long Answer Type Questions

Question.

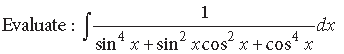
Answer.

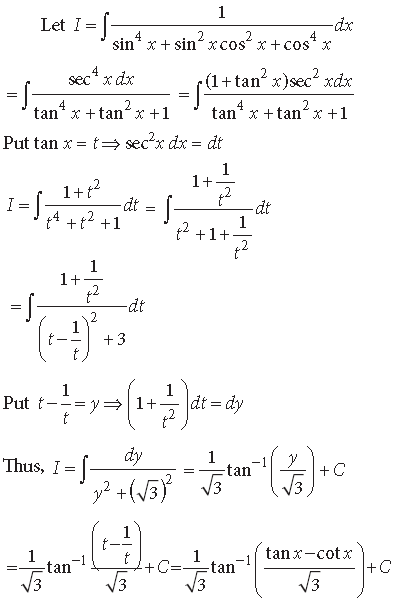
Question.

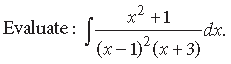
Answer.

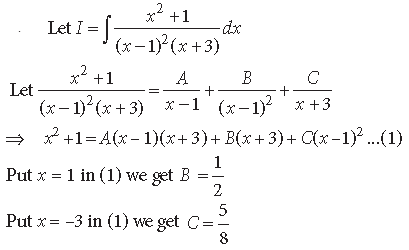
Question.

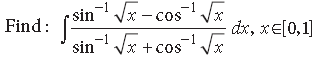
Answer.

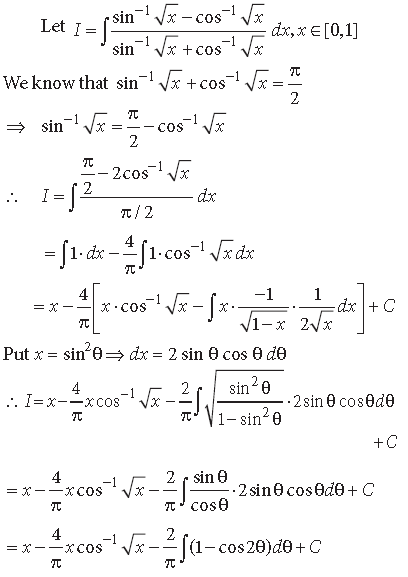
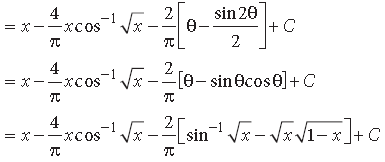
Question.

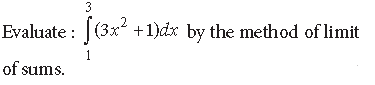
Answer. We have, by definition.

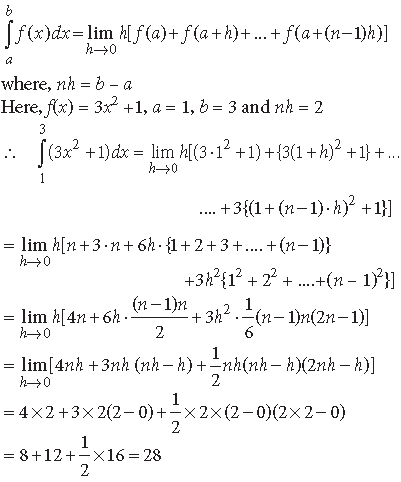
Question.

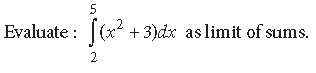
Answer. We have by definition,

Question.

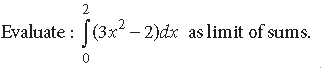
Answer. We have, by definition

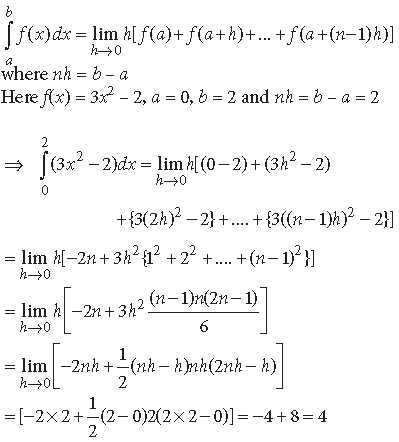
Question.

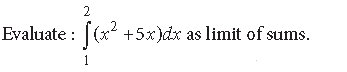
Answer. We have, by definition

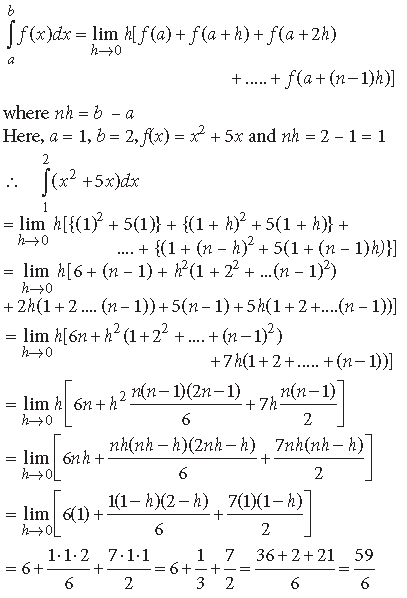
Question.

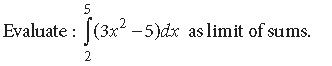
Answer. We have, by definition

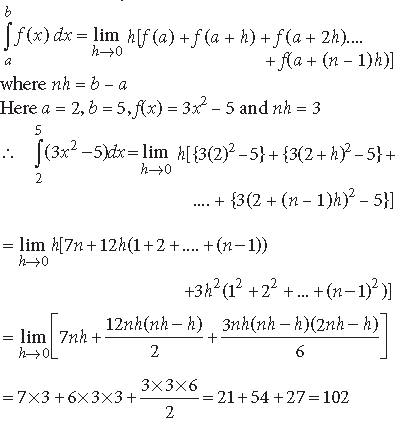
Question.

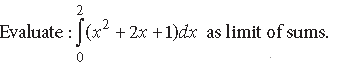
Answer. We have, by definition